声学波长波极限分析过程

"固体物理"根本概念和知识点第一章根本概念和知识点1) 什么是晶体、非晶体和多晶？(H)*晶面有规则、对称配置的固体，具有长程有序特点的固体称为晶体；在凝结过程中不经过结晶(即有序化)的阶段，原子的排列为长程无序的固体称为非晶体。

由许许多多个大小在微米量级的晶粒组成的固体，称为多晶。

2) 什么是原胞和晶胞？(H)*原胞是一个晶格最小的周期性单元，在有些情况下不能反响晶格的对称性；为了反响晶格的对称性，选取的较大的周期单元，称为晶胞。

3) 晶体共有几种晶系和布拉伐格子？(H)*按构造划分，晶体可分为7大晶系, 共14布拉伐格子。

4) 立方晶系有几种布拉伐格子？画出相应的格子。

(H)*立方晶系有简单立方、体心立方和面心立方三种布拉伐格子。

5) 什么是简单晶格和复式格子？分别举3个简单晶格和复式晶格的例子。

(H)*简单晶格中，一个原胞只包含一个原子，所有的原子在几何位置和化学性质上是完全等价的。

碱金属具有体心立方晶格构造；Au、Ag和Cu具有面心立方晶格构造，它们均为简单晶格复式格子则包含两种或两种以上的等价原子，不同等价原子各自构成一样的简单晶格，复式格子由它们的子晶格相套而成。

一种是不同原子或离子构成的晶体，如：NaCl、CsCl、ZnS等；一种是一样原子但几何位置不等价的原子构成的晶体，如：具有金刚石构造的C、Si、Ge等6) 钛酸钡是由几个何种简单晶格穿套形成的？(H)BaTiO在立方体的项角上是钡(Ba)，钛(Ti)位于体心，面心上是三组氧(O)。

三组氧(OI，OII，*3OIII)周围的情况各不一样，整个晶格是由 Ba、 Ti和 OI、 OII、 OIII各自组成的简立方构造子晶格(共5个)套构而成的。

7) 为什么金刚石是复式格子？金刚石原胞中有几个原子？晶胞中有几个原子？(H)*金刚石中有两种等价的C原子，即立方体中的8个顶角和6个面的中心的原子等价，体对角线1/4处的C原子等价。

声音的波长与频率的调节原理声音是一种机械波，它通过振动传递能量。

声音的波长和频率是描述声音波特性的两个重要参数。

1.波长：声音波长的定义是振动在介质中传播一个周期所经过的距离。

通常用符号λ表示，单位是米(m)。

波长与声音的传播速度有关，传播速度越快，波长越长。

2.频率：声音频率的定义是单位时间内声音波的振动次数。

通常用符号f表示，单位是赫兹(Hz)。

频率与声音的音高有关，频率越高，音高越高。

3.波长与频率的关系：根据波动方程v=λf（其中v表示波速，λ表示波长，f表示频率），波长和频率是成反比的关系。

当波速一定时，波长越长，频率越低；波长越短，频率越高。

4.声音的调节原理：声音的波长和频率可以通过调节声源的振动频率和介质的速度来实现。

例如，在空气中传播的声音，通过改变声源的振动频率可以产生不同音高的声音，而通过改变空气的速度（如吹气的力度）可以改变声音的波长和频率，从而产生不同音色的声音。

5.应用：声音的波长和频率在许多领域有重要的应用。

例如，在音乐领域，乐器的音高和音色与声音的波长和频率有关；在通信领域，无线电波的波长和频率用于调制和解调信号；在声学研究中，通过分析声音的波长和频率可以了解声波的传播特性和介质特性。

总结：声音的波长和频率是描述声音波特性的两个重要参数，它们之间有密切的关系。

通过调节声源的振动频率和介质的速度，可以改变声音的波长和频率，产生不同音高和音色的声音。

声音的波长和频率在各个领域有广泛的应用。

习题及方法：1.习题：一个频率为440Hz的声音在空气中传播，求该声音的波长。

解题思路：已知声音的频率为440Hz，空气中的声速大约为340m/s。

根据波动方程v=λf，可以求得该声音的波长。

解题方法：λ = v / f = 340m/s / 440Hz = 0.7727m答案：该声音的波长约为0.7727米。

2.习题：一个波长为1.5米的声音在空气中传播，求该声音的频率。

解题思路：已知声音的波长为1.5米，空气中的声速大约为340m/s。

声学波传播过程的数值模拟分析声学波传播是研究声波在不同介质中传播规律的一门学科。

通过数值模拟分析声学波的传播过程，我们可以更好地理解和预测声波在不同介质中的行为，为声学相关领域的研究和应用提供有力支持。

声学波传播的数值模拟分析首先需要确定所研究的问题，如声源的特性、介质的物理参数以及边界条件等。

然后，通过建立合适的数学模型和方程组，利用计算机进行数值计算和解析。

最后，根据模拟结果对声波传播过程进行分析和评估。

在声学波传播的数值模拟分析中，常用的方法包括有限差分法（FDM）、有限元法（FEM）和边界元法（BEM）等。

这些方法各有特点，可以根据具体问题和需求选择合适的方法进行模拟分析。

以有限差分法为例，它是一种离散化计算的方法。

首先，将声波传播问题的连续域转化为离散的有限差分网格，将时间和空间分割成小块。

然后，根据声学波动方程将声场的变化量用差分的形式表示。

最后，通过数值计算和迭代求解差分方程组，得到声场在各个时间和位置的数值解。

有限差分法的数值模拟分析具有一定的深度。

通过改变差分网格的分辨率，我们可以探究声波传播过程中的细节和特征。

例如，在分析声波在不同介质中的传播速度和衰减率时，可以通过调节网格大小和时间步长的方法来探讨它们对声波传播的影响。

此外，还可以研究声波在复杂介质结构中的传播规律，如声波在不同形状和密度的障碍物中的散射和衍射现象。

声学波传播的数值模拟分析还可以应用于声波在医学成像和工程设计中的研究。

例如，在医学领域中，数值模拟分析可以用于研究超声波在人体组织中的传播规律，以帮助医生进行准确的诊断和治疗。

在工程设计中，数值模拟分析可以用于研究声波在复杂环境中的传播特性，如建筑物中的声学设计和噪音控制。

当然，声学波传播的数值模拟分析也存在一些挑战和限制。

首先，模拟的精确度和计算效率之间存在着一定的平衡。

增加模拟的精度会导致计算量的增加，而过于追求计算效率可能会牺牲模拟的准确性。

其次，模拟结果往往需要与实验数据进行对比验证，以确保模拟的可靠性。

长波极限下声学波特点
通俗地讲就是：在长波极限下（q趋近0）：
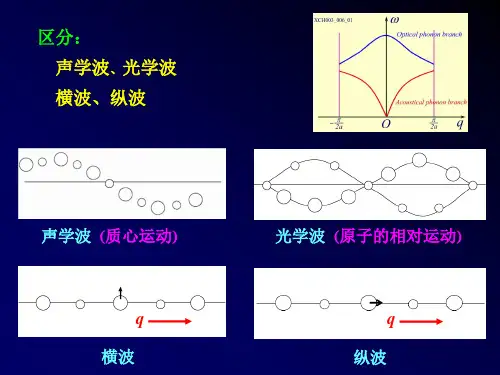
（1）对于光学波w+，有大小原子振幅比等于负的小大原子的质量比（B/A=-m/M）即Am+BM=0.所以光学波在长波极限下，描述的是原胞（大小原子）质心不动，大小原子相对于质心的振动，由于是负号，所以大小原子振幅方向相反，就像一个大人和一个小孩玩跷跷板一样，你上我下，你下我上。

“这就是你所问的描述的两个原子的运动！！！”
（2）对于声学波w-，有大小原子振幅比等于+1，即振幅大小和方向都相同。

所以大小原子可以看成是一个整体，就像一个大人抱着一个小孩一起挂在一根弹簧下，一起做上下振动。

就是原胞的质心在震动啦！“这就是你所问的一个原胞的振动，其实就是两个原子振动方向大小相同，看做是一个啦！。