下载文档原格式
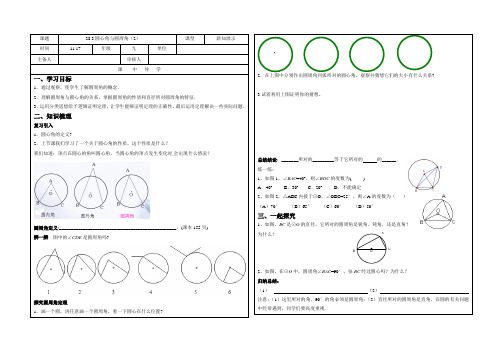
28.3 圆心角和圆周角┃教学整体设计┃第1课时圆心角┃教学过程设计┃二、师生互动,探究新知1.探究同圆中,圆心角、弧、弦的关系.展示折扇收拢的情景,提出问题.学生思考后回答.(1)观察折扇收拢的过程,哪些弧重合？弦重合？角重合？(2)由折扇得出的结论,在一般情况下还成立吗？如图,⊙O中,∠AOB＝∠COD,其余两组量AB与CD大小关系如何,弦AB与CD大小关系如何利用旋转思想解决问题.学生讨论、交流、展示.根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠COD的位置时,∠AOB＝∠COD,射线OA与OC重合,OB与OD重合.而同圆的半径相等,OA＝OC,OB＝OD,所以点A与点C重合,点B与点D重合.所以AB＝CD,AB＝CD.(3)在等圆⊙O1与⊙O2中,∠AO1B＝∠CO2D,那么AB与CD,AB＝CD分别相等吗？反过来,如果AB＝CD(或AB＝CD),那么∠AO1B与∠CO2D相等吗？为什么？师生总结：(1)在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧也相等.从生活中的折扇入手,让学生感受到数学与生活紧密联系,直观感知三组量之间的相等关系.┃教学小结┃┃教学整体设计┃ 第2课时 圆周角┃教学过程设计┃足球训练场上教练在球门前划了一个圆圈进行无人防守的射门训练.如图,甲、乙两名运动员分别在C,D两处,他们争论不休,都说自己所在位置对球门AB的张角大,如果你是教练,请评一评他们两个人谁的位置对球门AB的张角大？要想知道结果请同学们跟我一起学习这节课——圆周角.我相信学完之后大家都能回答这个问题.师生活动：教师在黑板上画出足球射门示意图,然后把生活问题抽象成数学问题. 探索激情和求知欲望,把学生的注意力尽快地转移到本节课的学习中来.二、师生互动,探究新知1.自学圆周角定义.观察图中的∠ABC,顶点在什么位置？角的两边有什么特点？圆周角的定义：顶点在圆上,两边都与圆相交的角叫做圆周角.注意：一个角是圆周角的条件：顶点在圆上；两边都和圆相交.2.探究同弧所对的圆周角与圆心之间的关系.请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角.学生思考、展示,再补充展示.师生活动：学生讨论、交流、做完及时地让老师查看.师生总结：圆周角定理：一条弧所对的圆周角等于它所对圆心角的一半.3.探究直径所对的圆周角是直角,90°的圆周角所对的弦是直径.(1)如图,BC是⊙O的直径,它所对的圆周角是锐角、直角,还是钝角？你是如何判断的？(2)图中,如果圆周角∠BAC＝90°,那么它所对的弦BC经过圆心O吗？为什么？师生活动：根据刚学习的知识,学生独立完成,通过学生自学,让学生初步了解圆周角的概念,培养学生的自学能力.并举手抢答.总结：直径所对的圆周角是直角；90°的圆周角所对的弦是直径.注意：这一推论应用非常广泛,一般地,如果题目的已知条件中有直径时,往往作出直径上的圆周角——直角；如果需要直角或证明垂直时,往往作出直径即可解决问题.4.同弧所对的圆周角相等.请同学们画一个圆,以A,C为端点的弧所对的圆周角有多少个？(至少画三个)它们的大小有什么关系？你是如何得到的？提示：用测量验证和运用圆周角与圆心角关系说理的方法说明它们的大小关系.师生活动：学生小组代表展示.归纳结论：同弧所对的圆周角相等.5.四边形与圆的关系.(1)四个顶点都在圆上的四边形叫做圆内接四边形.这个圆叫做四边形的外接圆.(2)四边形加上一个外接圆,四个内角变成四个圆周角,两组对角的大小有什么关系？(3)如图,观察外角∠DCE与∠A大小什么关系？为什么？学生通过画图,渗透分类讨论的思想,由特殊到一般解决问题的策略.┃教学小结┃。
