- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)要具备什么条件才能求解静电问题 (2)所求的解是否唯一
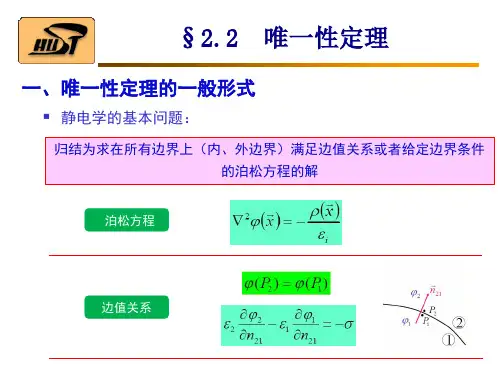
静电势的微分方程
2
边值关系 1 S 2 S
2
2
n
S
1
1
n
S
导体表面上的边值关系
|s 常数
n s
唯一性定理: 必须附加什么样的边界条件,泊松方程的解才会是唯一.
1) 绝缘介质静电问题的唯一性定理及证明 有限V 内有几种均匀的绝缘介质Vi 、εi (i = 1、2、3 …) , V 中的自由电荷分布(ρ或σ) 为已知
等式两端对V1 作体积分
111 dV1 1 1 2 dV1 1121dV
V1
V1
V1
式中 21 0
111 dV 111 dS 由高斯公式
V
s1
111 dS 1 1 2 dV1
s1
V1
111 dS 1 1 2 dV1
s1
V1
其中S1 为V1 的边界面,它由外边界1 和内边界两部分组成,即
以上的表达式,包括泊松方程、边值关系和边界条件统称 为定解问题. 唯一性定理指出,满足以上定解问题的电势解就是 区域V 中静电场分布的唯一解.
下面是对唯一性定理的证明。 首先证明区域V 中只有一种均匀介质的情况,然后再把它 推广到多种介质分区分布的情形。 a)区域V 中只有一种均匀介质的情形
利用反证法证明:假设区域V 中存在两个不同的解 '和''它
n S
s
dS
s
n
dS
0
2 dV 0
V
2 dV 0
V
注意到 2为非负数,欲使上式成立,只有 0 ,
即Φ= C ,或 ' - '' =C,
以上说明 ' 和 ''顶多差一个常数,而电势的附加常数对 电场没有影响,这就证明了 ' 和 ''在物理上是同一个解,
于是,唯一性定理得证.
b)区域V 中有两种各自均匀的介质ε1 和ε2 的情形 分别对应V1 区和V2 区
下面将证明,每一个区域的解都是唯一的.
对V1 区,设有两个解1 ' 、1 ' ' 都满足V1 区的场方程和边
界条件
令Φ1 = 1 ' - 1″ 则有,21 0 (在V1区内)
在V1区的外边界1上
1 外1 0
给定第一类边界条件
或 1 0
n1 外1
给定第二类边界条件
约定, n1 为V1 区边界的法向单位矢量,指向V1 外部;
dS
2 V2
2
2
dV2
11
内边界
1
n1
dS
11
1
n
dS
n1
n,
n2 n
22
内边界
2
n2
dS
22
2
n
dS
两式分别相加得
内边界11
1
n
2 2
2
n
dS
1
V1
1
2
dV1
2
V2
2
2
dV2
内边界11
1
n
2 2
2
n
dS
1
V1
1
2
dV1
2
V2
2
2
dV2
由电势的边值关系,在内边界上
同理对V2 区,设有两个解2'、2 ''都满足V2 区的场方程和
边界条件
令Φ2 = 2 ' - 2″
则有,22 0 (在V2区内)
在V2区的外边界2上
2 外2 0
给定第一类边界条件
或 2 0
n2 外2
给定第二类边界条件
约定, n2 为V2 区共界面(即内边界) 上,由电势的边值
2 1
2
2
n
1
1
n
1 1 2 dV1 2 2 2 dV2 0
V1
V2
欲使上式成立,只有 1 0 , 2 0 ,即1'和1'', 2'和2''顶多差一个常数,这说明,在每一个均匀小区内的
电场分布都是唯一的.
c)以上证明自然推广到含有两种以上均匀介质的情况
此时
1 1 2 dV1 2 2 2 dV2
关系
1 2 1 2
两式左右分别相减,得Φ1 = Φ2
又
2 2
2
n
2
n
1 1
两n11式 左 右相减,得:
n
2
2
n
1
1
n
n 为内边界上的法向单位矢,按约定由介质1 指向介质2
下面我们要证明, 1'和1 '', 2'和2''顶多都只能差一个常数
先看V1 区,利用微分恒等式
111 1 1 2 1121
V1
V2
n n 2 dVn 0 Vn
其中 V V1 V1 Vn
用类似的方法可以证明: 1 0,2 0,,从而区n 域 V0
中各处的电场分布一定是唯一的. 这样,关于绝缘介质静 电问题的唯一性定理得到了证明.
2)有导体存在的情况
设区域V 中有若干导体,其余部分都是一
种均匀介质ε,将扣除导体后的区域称为V′,V′的
111 dS 111 dS 111 dS
s1
外边界1
内边界
由前所述,外边界1 上的面积分为零
11
内边界
1
n1
dS
1
V1
1
2
dV1
同理,对区域V2 ,重复以上过程,可得到
22 内边界
2
n2
dS
2
V2
2
2
dV2
11
内边界
1
n1
dS
1
V1
1
2
dV1
22 内边界
2 n2
E
总结:
(P2 )
(P1)
P2 P1
E
dl
泊松方程 2
(
x)
( x)dV
4 0 r
,
()
0
介质: 导体:
1 S 2 S |s 常数
2
2
n
S
1
1
n
S
n s
总能量
W 1 E DdV 2
W
1 2
dV
§2.2 唯一性定理 Uniqueness Theorem
本节内容将回答两个问题:
们都能满足同一个泊松方程和边界条件,下面我们将证明 它们只能是同一个解.
引入标量函数Φ ,令Φ = '- ″
2 , 2 , 2 0
i
i
在区域边界面S 上
S
S
2 0 dV dS
V
s
0 S
(给定第一类边界条件)
或 ,
n S n S
n
0
S
(给定第二类边界条件)
下面需要证明的是,满足以上方程和边界条件的'和
''顶多只能差一个常数.
利用矢量的微分运算公式:
2 2 2
等式两端对V 作体积分
dV 2 dV 2dV
V
V
V
dV 2 dV 2dV
V
V
V
式中 2 0
dV dS
V
s
在边界面S 上,无论 S 0 还是 , 都0 使
当V 的边界面S 上的电势 (或电势法向导数)给定,
则V 内的电场有唯一确定的解。
数学表述如下:
2 i
i
(在每个小区Vi)
i j
(在两种绝缘介质的分界面上)
i
i
n
j
j
n
分界面法向单位矢量 n由 j指向i )
或 S n S
(在整个区域V 的边界面S上给定,按
约定,边界面法线 n指向V 外)