7相明(电磁场边值关系--唯一性定理)
- 格式:doc
- 大小:1.28 MB
- 文档页数:20




第一章标量三重积: 矢量三重积方向导:梯度:计算公式:矢量线方程:通量:散度:散度计算公式: 散度定理(高斯定理): 旋度:斯托克斯定理: 拉普拉斯运算:第二章电流连续性方程微分形式:对于恒定电流场: )()()(B A C A C B C B A⨯⋅=⨯⋅=⨯⋅CB A BC A C B A )()()(⋅-⋅=⨯⨯grad nu u en∂=∂zy x x y x∂∂+∂∂+∂∂=∇e e e ),,(d ),,(d ),,(d z y x F zz y x F y z y x F x z y x ==00cos cos cos |lim M l u u u u ul lx y z αβγ∆→∂∆∂∂∂==++∂∆∂∂∂d d d n SSψψF S F e S==⋅=⋅⎰⎰⎰ττ∆⋅=⎰→∆SSd F div F lim 0z F y F x F Sd F div z y x S ⋅∇=∂∂+∂∂+∂∂=∆⋅=⎰→∆ττF lim⎰⎰⋅∇=⋅VSVF S F d dmax ]rot [F e F n n =⨯∇zy x z y xF F F z y xe e e F ∂∂∂∂∂∂=⨯∇=⎰⎰⋅⨯∇=⋅SCS F l F d d )()(2F F F ⨯∇⨯∇-⋅∇∇=∇uu 2)(∇=∇⋅∇0d ⎰=⋅SS J 、0=⋅∇JtJ ∂∂-=⋅∇ρ静电场散度:高斯定理的积分形式: 静电场旋度:毕奥萨法尔定律:任意电流回路 C 产生的磁感应强度恒定磁场散度: 恒定磁场是无散场恒定磁场旋度: 恒定磁场是有旋场,它在任意点的旋度与该点的电流密度成正比,电流是磁 场的旋涡源。
极化强度:----------电介质的电极化率电位移矢量:电介质中高斯定理的积分形式: 磁化强度矢量: 磁化电流体密度: 真空中安培环路定理推广到磁介质中: 磁场强度 :M B H-=0μ麦克斯韦方程组的微分形式传导电流和变化的电场都能产生涡旋磁场。




第一章电磁现象的普遍规律 一、 主要内容:电磁场可用两个矢量一电场强度电Z,zQ 和磁感应强度B{x r y r zfy 来完全 描写,这一章的主要任务是:在实验定律的根底上找出丘,歹所满足的偏微分方程组 一麦克斯韦方程组以及洛仑兹力公式,并讨论介质的电磁性质及电磁场的能量。
在电 磁学的根底上从实验定律岀发运用矢量分析得出电磁场运动的普遍规律:使学生掌握 麦克斯韦方程的微分形式及物理意义;同时体会电动力学研究问题的方法,从特殊到 一般,由实验定律加假设总结出麦克斯韦方程。
完成由普通物理到理论物理的自然过 渡。
二、 知识体系:介质磁化规律:能量守恒定律n 线性介质能量密度:I 能流密度:洛仑兹力密度;宇二应+" x B三、内容提要:1. 电磁场的根本实验定律:(1) 库仑定律:库仑定理:壮丿=[*虫1厶电磁感应定律:市总•屋=-—[B-dSdV f區 dt k涡旋电场假设 介质的极化规律:V- 5 = /? VxZ=比奥-萨伐尔逹律: D = s Q S + PJdVxr边值关系位移电流假设V-> = 0J+ —B =其中:第2页,共37页对E 个点电荷在空间某点的场强等于各点电荷单独存在时在该点场强的矢量和, 即:〔2〕毕奥——萨伐尔定律〔电流决定磁场的实验定律〕B = ^[^L〔3〕电磁感应定律②磁场与它激发的电场间关系是电磁感应定律的微分形式。
〔4〕电荷守恒的实验定律①反映空间某点Q 与了之间的变化关系,非稳恒电流线不闭合。
空二0月•了二0②假设空间各点Q 与£无关,那么別为稳恒电流,电流线闭合。
稳恒电流是无源的〔流线闭合〕,°, 7均与北无关,它产生的场也与上无关。
2、电磁场的普遍规律一麦克斯韦方程微分形式di——diV • D = p方二勺宜+戶,H = —-MAo积分形式[f] E dl =-\ --dSSJs 冼[fl H-df = I + -\D -d§S念J血Q/40①生电场为有旋场〔鸟又称漩涡场〕,与静电场堤本质不同。

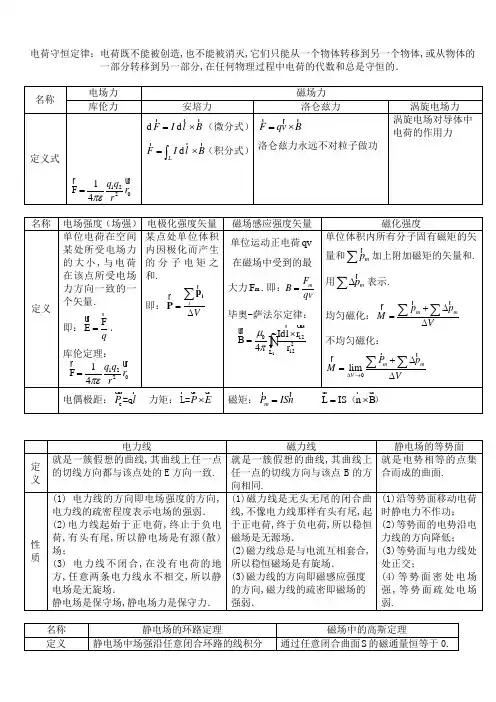
电荷守恒定律:电荷既不能被创造,也不能被消灭,它们只能从一个物体转移到另一个物体,或从物体的一部分转移到另一部分,在任何物理过程中电荷的代数和总是守恒的.名称电场力 磁场力库伦力 安培力 洛仑兹力 涡旋电场力定义式12021F 4q q r rπε=d d F I l B =⨯(微分式)d L F I l B =⨯⎰(积分式)F qv B =⨯ 洛仑兹力永远不对粒子做功 涡旋电场对导体中电荷的作用力名称 电场强度(场强)电极化强度矢量 磁场感应强度矢量 磁化强度定义单位电荷在空间某处所受电场力的大小,与电荷在该点所受电场力方向一致的一个矢量.即:FE q=.库伦定理:12021F 4q q r r πε=某点处单位体积内因极化而产生的分子电矩之和.即:i V =∆∑i p P单位运动正电荷qv在磁场中受到的最大力m F .即:mF B qv= 毕奥-萨法尔定律:112212L Idl r B 4r μπ⨯=⎰单位体积内所有分子固有磁矩的矢量和m p ∑加上附加磁矩的矢量和.用m p ∆∑表示. 均匀磁化:mmp pM V+∆=∆∑∑不均匀磁化:limmmV P p M V∆→+∆=∆∑∑电偶极距:e P l =q 力矩:P E ⨯L=磁矩:m P ISn = L IS n B =⨯()电力线 磁力线 静电场的等势面定义就是一簇假想的曲线,其曲线上任一点的切线方向都与该点处的E 方向一致. 就是一簇假想的曲线,其曲线上任一点的切线方向与该点B 的方向相同.就是电势相等的点集合而成的曲面. 性质(1) 电力线的方向即电场强度的方向,电力线的疏密程度表示电场的强弱. (2)电力线起始于正电荷,终止于负电荷,有头有尾,所以静电场是有源(散)场; (3) 电力线不闭合,在没有电荷的地方,任意两条电力线永不相交,所以静电场是无旋场. 静电场是保守场,静电场力是保守力. (1)磁力线是无头无尾的闭合曲线,不像电力线那样有头有尾,起于正电荷,终于负电荷,所以稳恒磁场是无源场. (2)磁力线总是与电流互相套合,所以稳恒磁场是有旋场. (3)磁力线的方向即磁感应强度的方向,磁力线的疏密即磁场的强弱. (1)沿等势面移动电荷时静电力不作功; (2)等势面的电势沿电力线的方向降低; (3)等势面与电力线处处正交; (4)等势面密处电场强,等势面疏处电场弱.名称 静电场的环路定理 磁场中的高斯定理 定义 静电场中场强沿任意闭合环路的线积分通过任意闭合曲面S 的磁通量恒等于0.人生在搏,不索何获渭南师院08级物理学班刘占利 2009-9-221(称作环量)恒等于零.即:d 0LE l ⋅=⎰. 即:SB dS 0⋅=⎰⎰说明的问题电场的无旋性磁场的无源性电位差(电压):单位正电荷的电位能差.即:B AB ABABA W A U Edl q q===⎰.磁介质:在磁场中影响原磁场的物质称为磁介质.名称 电通量 磁通量定义 电通量就是垂直通过某一面积的电力线的条数,用 e Φ表示.即:SSe E dS EdScos θΦ==⎰⎰⎰⎰垂直通过某曲面磁力线的条数叫磁通量,用m Φ表示.即:SSm B dS BdScos θΦ==⎰⎰⎰⎰名称 静电感应 磁化定义 电场对电场中的物质的作用 磁场对磁场中的物质的作用在介质中求电(磁)场感应强度:方法 利用电介质时电场的高斯定理求电场感应强度利用磁介质中的安培环路定理求磁场感应强度 原理通过电介质中任一闭合曲面的电位移通量等于该面包围的自由电荷的代数和.0d SS q ⋅=∑⎰D S 内0ε=+D E PP n δ=⋅e 0P E χε=(各向同性介质)e 1r εχ=+0r εεε==D E E磁场强度沿任意闭合路径的线积分(环量)等于穿过以该路径为边界的面的所有传导电流的代数和,而与磁化电流无关.d H l I ⋅=∑⎰BH M μ=-M j n =⋅m M H χ=(各向同性介质)1r m μχ=+0H r B H μμμ==解题步骤(1)分析自由电荷分布的对称性,选择适当的高斯面,求出电位移矢量D .(2)根据电位移矢量D 与电场E 的关系,求出电场E . (3)根据电极化强度P 与电场E 的关系,求出(1)分析传导电流分布的对称性,选择适当的环路,求出磁场强度H .(2)根据磁场强度H 与磁场感应强度矢量B 的关系,求出磁场感应强度矢量B .(3)根据磁化强度M 与磁场感应强度矢量B 的2电极化强度P . (4)根据束缚电荷e δ与电极化强度P 关系,求出束缚电荷e δ.关系,求出磁场强度M .(4)根据磁化电流0I 与磁化强度M 关系,求出磁化电流0I .电(磁)场能量: 电场 磁场 电磁波能量密度 e 1D E 2ω=⋅ m 1B H 2ω=⋅ 22221()2e m w w w E H E H εμεμ=+=+==能量 2e 11W D EdV=CU 22=⋅⎰⎰⎰ 2m 11W B HdV=LI 22=⋅⎰⎰⎰ m W D EdV=B HdV =⋅⋅⎰⎰⎰⎰⎰⎰位移电流与传导电流比较静电场 涡旋电场 传导电流 位移电流不同点电荷 变化的磁场 自由电荷运动 变化的电场电力线不闭和 电力线闭和 产生焦耳热 不产生焦耳热相同点 对电荷都有力的作用 产生等效的磁效应四种电动势的比较: 电动势 产生原因 计算公式 动生 洛仑兹力:q F v B =⨯d i Lv B l ε=⨯⋅⎰感生涡旋电场力:F qE =涡i d d d d L SB E l S t ε=⋅=-⋅⎰⎰⎰自感自身电流变化:m N LI Φ= i d d ILt ε=- 互感 相互电流变化:211MI φ= 122MI φ= 121d d I M t ε=- 212d d IM tε=- 关系:12L L M k = 楞次定律:闭合回路中感应电流的方向,总是使得它所激发的磁场来阻止引起感应电流的磁通量的变化。

5ξ电磁场的边值关系一.引言当介质分布均匀时,出现了界面,→D ,→B 有跃变,界面两侧场值的关系 1.边值关系:描述介质界面两侧的场矢量与界面上电荷,电流的关系 2.麦氏方程组的微分形式要求→E ,→D ,→B ,→H 在介质中连续麦氏方程组的积分形式在场量不连续时不成立。
故不能用微分形式导出边值关系,而用积分形式讨论边值关系。
⎪⎪⎪⎭⎪⎪⎪⎬⎫=∙=∙⎰⎰⎰→→→→s s v S d B dv S d D 0ρ⇒导出法向关系⎪⎪⎪⎭⎪⎪⎪⎬⎫∙∂∂+∙=∙∙∂∂-=∙⎰⎰⎰⎰⎰→→→→→→→→→→s s l l S d t DS d j l d H S d tB l d E ⇒导出切向关系二.边值关系(法向关系证明从略,切向关系讲一例后推论) 1.→D 的法向有跃变⎰⎰=∙→→vsdv S d D ρ⇒σfD D n =-∙→→→)(12 (1)推论:εσσρρε0120)()(1pf v pf sE E n dv S d E +=-∙⇒+=∙→→→→→⎰⎰ (2)dv S d P ps⎰⎰-=∙→→ρ→⇒n )(12→→-∙P P =-σP(3)2.→B 的法向连续0)(0)(0112212=-∙−−−−→−=-∙⇒=∙→→→→→→→→⎰H u H u B B n n S d B s线性各向同性(4) 3.的→E 切向连续→→→→∙-=∙⎰⎰S d B dt d l d E s l 0)(12=-⨯⇒→→→E E n E Et t12= (5)4.的切向跃变→H→→→→→→→→→→=-⨯⇒∙∂∂+∙=∙⎰⎰⎰αf sflH H jn s d t DS d l d H )(12 (6)0)(012=-⨯=→→→→H H n f时,αH Ht t12= (7)线性各向同性:uB uBtt 1122=(8)推论:→→→→→→→→=-⨯⇒∙=∙⎰⎰αm s Ml M M jn S d l d M )(12 (9)5.→jf的法向跃变⎰⎰-=∙→→dv dt dS d sfjρtn f f f jj ∂∂-=-∙⇒→→→σ)(12 (10)0=∂∂t时,0)(12=-∙→→→jj f f n (11)三.说明1.上述关系在介质界面静止时导出,运动时,D ,B 法向关系仍成立,但E ,H切向改变2.规定:界面法向n从介质1指向介质2,否则差一负号3.具普遍意义:对任意矢量场,只要场方程与麦式方程组形式相同,其边值关系亦相同。
如∙∇→P =-Pρ⇒n ∙(→P -→P )=-σP4.三个特殊参数:ε,u,σ描述介质的电磁性质。
三参数中只要有一个不同,则为不同介质,其交接面为介质界面,ε不同会出现σP,σ不同会出现自由电荷,μ不同会出现→M α。
5.导电介质的恒定电场问题(47P 11T )恒定电场:由恒定电荷产生的电场恒定电荷指系统内电荷恒定(并非电荷不动!)微分方程式: ∙∇j=0 (12)→⨯∇E =0(13)j=σE (电源除外)(14)6.静电场中的导体→内E =0 n ∴ ⨯E=0对稳恒电流 n ∙(2j -1j)=0 48P 13T四 证明只证明H的切向边值关系在界面两侧较狭长矩形回路积分回路绕行方向∥→αf,矩形短边→0∴→→∙⎰l d H l=(2H -1H)∙→∆lstd D d ⎰∙d s 0→s 0 f I =→→→∆∙⨯=∆∙l n l f f )(αα由→→∙⎰l d H l =→→∙⎰S d sfj+s d D d S dt ∙⎰ =f I +sd D d S dt ∙⎰有(2H -1H)→∆∙l =(→→⨯n f α)→∆∙ll ∆任意∴ (2H -1H )∥=f n α⨯ 有:⨯→n (2H -1H)∥=⨯→n (f n α⨯ )而 n ⨯ (2H -1H )∥=n ⨯ (2H -1H)n ⨯(2H -1H )=n ⨯(f nα∙ )=fα(n n∙ )-→n (fn α∙ )=fα证毕注:面电流密度为垂直通过单位横截线的电流即电流线密度书上:47P T9 12 ,13 补充:证明E的切向关系(本科生补充题:当介质界面上不仅有存在自由电荷,并且存在传导面电流时,试导出与电荷守恒定律相应的边值关系)6ξ 电磁场的能量和能流一.过去对电磁能的认识 1.电能点电荷间: e U =124o q q rπε 电容器: e U =212q C =qV 21电能密度: e W =2012E ε2.磁能电感: m U =212IL 磁能密度: m W =212B u3.静电静磁条件下,电磁能的特点:1形式上:q,E ,B,I 表现2问题:①电磁能究竟定域在哪?是不确定的! ②只有一个参量描述 W ③能量守恒二.普遍情况下电磁过程中能量的转化和守恒定律 麦克斯韦方程组揭示:一般情况下,电磁场两个特点:场可以脱离源———能量定域在场中场的运动———两个参量描述场能W,S1.概念1 能量密度W (x,t ):电磁场单位体积内的能量2 能量密度S(坡印延矢量):单位时间通过与波传播方向垂直的单位横截面的能量2.电磁现象中能量守恒定律的表现形式10表述 电磁场运动的某空间区域V 内,单位时间通过V 表面S 流入V 内的能量等于场对该区域所做的功率与V 内电磁能量的增加率之和 20导出,⑴场对V 内自由电荷所作的功率对单位体积所作功率:f v ∙该部分能量变成电荷的功能或焦耳热 , 其中f=ρ(E +V B ∙ )对V : vf vdv ∙⎰⑵V 内场能量的增加率单位体积w t ∂∂ dv :wdV t∂∂ V :vw dV t ∂∂⎰ ⑶流入S 的能量d s :s ds ∙s :-→→∙⎰s d S (“-”表示流入)积分式-→→∙⎰s d S S=v f vdv ∙⎰ +v w dv t ∂∂⎰⑴-v v s dv ∙∙⎰ =v f vdv ∙⎰ +vwdv t ∂∂⎰微分式: -s ∇∙ =f v ∙ +wt∂∂⑵⑷特殊情况若无能量导入,即s=0,则f v ∙ =-w t∂∂ ⑶三,s,w 的表达式1.导出:由⑴式-v wdV t ∂∂⎰-→→∙⎰s d S S =v f vdv ∙⎰思路:从vf vdv ∙⎰入手找出其用场量表示的结果,与左边比较得出 vf vdv ∙⎰ =[()]vE V v B v dV ρρ∙+∙∙⎰=VE jdV ∙⎰=()VDE H dV t ∂∙∇⨯-∂⎰ ()D H j t ∂∇⨯=+∂利用()()()A B B A A B ∇∙⨯=∙∇⨯-∙∇⨯有343(P I 21)()()()()V V VBD E H H E H E E H dV H dV E dVt t →∂∂⋅∇⨯=∇∙⨯+∙∇⨯=-∇∙⨯-∙-∙∂∂⎰⎰⎰=()()()S VB B DE H H E H d S H E dV t t t →∂∂∂-∇∙⨯+∙-=-⨯∙-∙+∙∂∂∂⎰⎰⑸⑷与⑸比较 S E H →=⨯⑹w B DH E t t t∂∂∂=∙+∙∂∂∂⑺V S Vwf vdV S ds dV t →∂∙=-∙-∂⎰⎰⎰2.论证⑴能量定域在场中(有场就有能量)⑵能量是守恒的(机械能+电磁能)————场是物质的 ⑶全空间能量守恒律形式无穷 处 0E = 0H =, ()0E H d S →→∞⨯∙=⎰∴ Vvdf vdV wdv dt ∙=-⎰⎰⑻意义:单位时间内机械能的增加等于全空间总能量的减少⑷真实情况O D E ε=, 0B H μ=220000122E W B B B EE t u t t t tεεμ∂∂∂∂∂=∙+∙=+∂∂∂∂∂ =220011()22B E t εμ→∂+∂∴ 22001122em m e W B E W w w εμ=+⇒=+ ⑼ 1os E H E B μ=⨯=⨯⑽⑸介质情况j E H =⨯W D BE H t t t∂∂∂=∙+∙∂∂∂0D E P ε=+ ,01H B M μ=-对线性各向同性介质: D =E ε∙ B H μ= D ∥E B ∥H同理有 221122em m e W B E W W εμ=+=+介介介 ⑾=1()2H B E D ∙+∙与真空比较:e r e e W W W ε=>介222201111()2222m r r m m W B H H H W W μμμμμμμ=====>介 结论:①真空与介质的电磁能密度不同②真空中:电磁能+磁场能介质中:电场能+磁场能+极化能+磁化能原因是介质中 f ρ ,f j , ρρ , p σ ,m j ,p j p j电磁场对ρρ ,P σ和m j要做功,转化为极化能和磁化能储存在介质中,若介质无损耗(铜损,铁损),它们是可逆的。
四.电磁能的传输1.稳恒电磁场(直流情况)0wt∂=∂ 自由电荷动能不变,故f ,v 完全转化为焦耳热 ∴ VSf vdV S d s →∙=-∙⎰⎰流入V 中的电磁能全部转化为对电荷作功——完全转化为焦耳热∵2f v j E E E E σσ∙=∙=∙∙==2j σ22VVj j f vdV dV V σσ∙==⎰⎰对柱形体:222222j j j s I V sl l l I R s sσσσσ====能量的传输:能量在场中传输 直流电路j nev =- , 283108.4n m=⨯ 191.610e C -=-⨯ 319.110e m kg -=⨯622101AA j mm m ==5105m v s-=⨯ ek E 很小又j 处处相等,ek E 不变,若灯光内ek E 转化而来则与I(j)处处相等矛盾,灯光的能量从何而来? 分析电路,接连K 时,电路中I,V B ⇒ ,K ,灯光能量正是由电磁场传输的能量交交情况:广播,电视是从电磁场接收能量的广播,电视发对天线附近压,用一段导线可使电灯发亮 因此,无论直流或交流电路,导线的直接作用是引导电磁场传输例1 43p 例2 例3 48P 14T解 非磁性物质,故介质性质为ε,σ 积分式解法微分式解法⑴取单位长同轴圆柱高斯面(a r b <<) 由高斯定理得22f E r rλπε=则f SQ D d s →=∙⎰212f D E rj t t rλεπ∂∂==∂∂fSdQ D d s dt t →∂=∙∂⎰ 由传导电流定义I=f f dQ d l dtdt λ=又由电荷守恒定律电荷守恒律ff SdQ j d s dt→∙=-⎰ff SdQ j d s dt→∙=-⎰2f f d j rl l dtλπ=-r j f π21-=fd dtλ∴f S SD j d s d s t →→∂∙=-∙∂⎰⎰ 212f f d rj dt r λπ→=-()()0f f d s SD j d s j j d s t →→∂+∙=+∙=∂⎰⎰ ∴ f d j j o += ∴0f D j j +=而 0f D H j j ∇⨯=+=∴ B O ∇⨯=又 0B ∇∙=∴0B =⑵f f f SVdQ dj ds dV dt dt ρ→∙=-=-⎰⎰又22f f j E r r σλσπε===-f f ddl dl dt t λλ∂-=-∂⎰⎰即122ff d r dt rλσλππε-=-由f j E σ=,f SS Sj d s E d s D d s σσε→→→∙=∙=∙⎰⎰⎰ f f d dt λσλε=- =f dl σλε⎰ffd dt λσλε=-∴ff f f d dt t λλσσλελε∂=-⇒=-∂ t f fo e σελλ-=tf fo eσελλ-=-*参见梁绍荣,电动力学,北师大出版社1986年3334P - ⑶法1:能量的耗散转化为焦耳热法2: 0B =由焦耳一楞茨定律2e W E t σ∂=∂ ∴能量密度的变化率e W D E E E t t tε∂∂∂=∙=∙∂∂∂故能量耗散功率密度为=-2()2f rλσπε+2()2f ew p t rλσπε∂=+=∂故能量耗散率密度eW t ρ∂=-∂ 2()2f rλρσπε= 式中eW t∂∂为热功率密度 或电磁场对电荷做功完全转化为焦耳热,耗 ⑷对长为L 的一段介质总能量耗散功率 散功率密度为 →→→→→=∙=∙E E j v f f σ2()22f ev vW dv ldr t r λρσππε∂==∂⎰⎰ 2)2(r v f f πελσ=∙→→而对l 一段有=2222222b f f n a l l dr b r a σλσλπεπε=⎰ 2v vf vdv E dv σ∙=⎰⎰ 另一方面,静电能'1e f W lv λε= =22()22bf arldr λσππε⎰22bb f f n a abV E dr dr r a λλπεπε=∙==⎰⎰ =22f n l b a σλαπε ∴2'4f e n l bW aλπε=0s =由电磁能量守恒有2'222f ff e n n l d l W b b t a dt a λλσλπεπε∂==-∂ v vw f vdv dv t ∂∙=-∂⎰⎰ ∴'e e W W t t∂∂=-∂∂ew dv t∂=-∂⎰作业:试证麦式方程组中D ρ∇∙=不独立 即场对电荷所作的总功率等于其静电能()()0DH j j D t t∂∂∇∙∇⨯=∇∙+∇∙=∇∙+∇∙=∂∂的减少又0j tρ∂∇∙+=∂ 两式化较得:D ρ∇∙=2.试证麦式方程组中0B ∇∙=不独立 ()()()0B E B t t∂∂∇∙∇⨯=∇∙-=-∇∙=∂∂0B ∴∇∙= (本应B C ∇∙=,但方程中给出C=0)3 试证麦式方程组中蕴含了电荷守恒律4 48P 14T5 试由麦克斯韦方程导出电磁场能量密度和动量密度的表达式6 47P 11T (提示:要用到稳恒条件下边界上的电荷守恒定律)第二章 静电场第二章,第三章的中心问题:给定源分命,空间介质,导体分布条件下求解E ,B方法:将麦式方程组的矢量方程转化为标量方程(7个)方程,静场条件下引入势——静电势,磁矢势,磁标势,导出势的微分方程,在一定边界条件下求解势的微分方程。