下载文档原格式
两端固定挠曲线微分方程
两端固定挠曲线是指一根杆件或梁在两端被固定，并在加载下发生弯曲的情况。
对于一维情况下的挠曲，可以使用梁的挠曲理论来描述。
梁的挠曲可以通过微分方程来表示。
对于一根杆件或梁，假设其长度为L，横截面面积为A，杨氏模量为E，惯性矩为I，单位长度上的弯矩为M(x)，单位长度上的剪力为V(x)，梁的挠度为w(x)，则可以得到以下微分方程：
EIw''''(x) = M(x)。
其中，w''''(x)表示挠度w(x)关于x的四阶导数。
这个微分方程描述了梁在两端固定情况下的挠曲行为。
根据具体的加载情况和边界条件，可以求解出梁的挠度分布。
在实际问题中，通常需要根据具体的加载和边界条件来确定单位长度上的弯矩M(x)。
例如，如果梁在两端承受均布载荷，则单位长度上的弯矩可以表示为M(x) = qLx (qL/2)x^2，其中q为均布载荷。
通过求解上述微分方程，可以得到梁的挠度分布w(x)，进而可
以计算出梁的弯曲角度和剪力分布等重要参数。
这些参数对于设计
和分析梁的结构具有重要意义。
总结起来，两端固定挠曲线的微分方程是EIw''''(x) = M(x)，其中EI为梁的弯曲刚度，w(x)为梁的挠度，M(x)为单位长度上的弯矩。
根据具体的加载和边界条件，可以求解出梁的挠度分布，进而
得到梁的弯曲角度和剪力分布等参数。
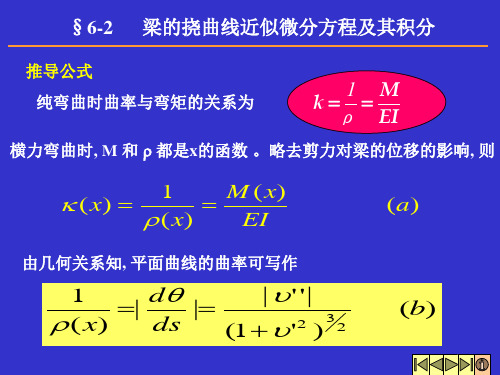
挠曲线近似微分方程微分方程是描述曲线变化的数学工具。
在实际应用中，有时候我们需要对非常复杂的曲线进行近似处理，以便更好地对其进行研究和分析。
挠曲线近似微分方程就是其中一种常用的方法。
挠曲线是欧几里德空间中的一种特殊曲线，它的性质使得它在工程、物理学和数学等领域具有重要的应用。
例如，在杆、梁和桥梁等结构的力学分析中，挠曲线可以帮助我们计算和预测结构的变形和应力分布。
当我们研究挠曲线时，我们通常关注它在不同点的曲率或者弯曲情况。
这些信息对于结构的稳定性和性能至关重要。
因此，我们需要一种方法来描述和计算曲线的弯曲程度。
首先，我们定义曲线的弯曲长度$dL$，它等于曲线在无限小线段上的长度：$$dL=\sqrt{1+(y')^2}dx$$其中，$y'$表示曲线在$x$处的斜率。
然后，我们定义曲率$\kappa$为曲线在无限小线段上的弯曲长度与线段长度之比：$$\kappa=\frac{1}{R}=\frac{dL}{ds}=\frac{\sqrt{1+(y')^2}}{ds}$$其中，$R$表示曲线的半径，$ds$表示线段的长度。
这样，我们可以得到曲率与曲线的导数之间的关系：$$\kappa=\frac{d^2y}{dx^2}\frac{1}{[1+(y')^2]^\frac{3}{2}}$$这就是挠曲线的近似微分方程。
通过求解这个微分方程，我们可以得到曲线在不同点的曲率，从而了解曲线的弯曲情况。
挠曲线近似微分方程在工程、物理学和数学等领域广泛应用。
通过该方法，我们可以计算和预测结构的变形和应力分布，从而帮助我们设计更稳定和高效的结构。
同时，在数学研究中，挠曲线近似微分方程也提供了一种处理复杂曲线的方法，为曲线的研究和分析提供了有力的工具。
总之，挠曲线近似微分方程是一种用来描述曲线弯曲情况的方法。
通过将曲线划分为无限小的线段，并在每个线段上定义曲率，我们可以使用微分方程的方法来计算整个曲线的弯曲情况。
