当前位置：文档之家 › 梁的挠曲线近似微分方程及其积分

梁的挠曲线近似微分方程及其积分

  • 格式：ppt
  • 大小：6.02 MB
  • 文档页数：70

下载文档原格式

  / 70

合集下载

梁的挠度及转角(1)

梁的挠度及转角(1)

A2= mL/6EI B2= - mL/3EI
yc2 = mL2/16EI
力的分解法----各横截面的位移或转角等 于每项荷载独立作用时在同位置产生的挠 度和转角代数和。
A= A1+ A2= FL2/16EI + mL/6EI
B= B1+ B2= - FL2/16EI - mL/3EI
yc= yc1 + yc2 = FL3/48EI +mL2/16EI
2）M(x)是连续函数。
3）梁的变形是在线弹性小变形范围内。
4)
0
x
5.EXANPEL y
例5-1：求悬臂梁B截面的转角和B截面挠度， 设 ：梁长为L，EI = 常数 。
Ax
F ①求约束反力 YA=F mA= FL
x
B ②列弯矩方程 M(x)=Fx-FL
③列挠曲线近似微分方程
yM (x)F(Lx) EI EI
1. 叠加原理的适用范围 2.叠加原理
1)力的分解法-2)梁的分段法--
1. 叠加原理的适用范围
在材料的线弹性范围内，梁的小变形且纵向变形忽略不计的条件下，梁的 挠度和转角与作用在梁上的荷载成线性关系.
2.叠加原理—
１）梁在几项荷载同时作用下某一横截面 的挠度和转角，可等于每一项荷载单独作 用下该截面的挠度和转角的叠加．
1.弯曲变形的弊与利 2.挠曲线（deflection curve) 3.挠度和转角方程(equation of deflection and slope) 4.弯曲位移的符号规则
1.弯曲变形的弊与利
Fp
Fp
q
2Fp
❖❖❖使利设结用计构变成的形弯使的曲用物形功理以能条达受件到到求减影弯震象曲，，静减严不少重定动时问载会题荷破。。坏。
概述梁的挠曲线近似微分方程及其积分用积分

概述梁的挠曲线近似微分方程及其积分用积分


x 0 时， ， wA 0 A w A 0
当
求得：
C 0; D 0
y
L
P
B
B
wB
x
写出挠曲线方程并画出挠曲线的大致形状
Px 2 w( x) ( x 3L) 6EI
最大转角及最大挠度（绝对值最大）
max
PL2 B （ ） 2 EI
wmax
PL3 wB （ ） 3EI
C
x1
x2
AB段 (0 x1 a)
a
a
M1 Px1
BC段 (0 x2 a)
M 2 P(a x2 )
写出挠曲线微分方程并积分 AB段
M1 Px1 EIw1
P 2 EI1 x1 C1 EIw1 2 P 3 EIw x1 C1 x1 D1 6
1
y
M<0
d2w 0 2 dx
d2w M ( x) 2 EI dx
o
x
d 2 w M ( x) (2) 2 EI dx
式（2）就是挠曲线近似微分方程。
对于等截面直梁，挠曲线近似微分方程可写成如下形式：
d w M ( x) 2 EI dx
二、求转角方程、挠曲线方程 1.微分方程的积分
最大挠度及最大转角
dw( x 2 ) Pa 2 ( x2 ) dx 2 2 EI
2
y
a
P
C
C
max C CB
wmax
Pa 2 2EI
L
B
x
wB
Pa 2 wB (3L a) 6EI
例2 求图示梁自由端的转角和挠度。
讲梁的挠曲线方程与积分解法

讲梁的挠曲线方程与积分解法


②积分常数的确定——边界条件和连续条件：
边界条件：梁在其支承处的挠度或转角是已知的， 这样的已知条件称为边界条件。 连续条件：梁的挠曲线是一条连续、光滑、平坦 的曲线。因此，在梁的同一截面上不可能有两个 不同的挠度值或转角值，这样的已知条件称为连 续条件。
边界条件
积分常数2n个=2n个
连续条件
列出图示结构的边界条件和连续条件。
8
代入（1）（2）得：
1 ( 1 qx3 1 qL3)
EI 6 6
1 ( 1 qx4 qL3 x qL4 )
EI 24
68
将 x 0 代入得：
A
qL3 6EI
（与C比较知E：I A C）
A
qL4 8EI
（与D比较知E：IA ）D
因此
常数C表示起始截面的转角×刚度(EI)
常数D表示起始截面的挠度×刚度(EI)
x L
2
2、
d 2
dx 2
M (x) EI z
EI" 1 qx2
2
积分一次： EI' EI 1 qx3 C （1）
积分二次：
6
EI 1 qx4 Cx D （2）
24
B X``
3、确定常数C、D.
由边界条件： x L, 0 代入（1）得： C 1 qL3
6
x L, y 0 代入（2）得： D 1 qL4
支座反力，分段列弯矩方程； 分段的原则:
①凡载荷有突变处（包括中间支座），应作为分段点；
②凡截面有变化处，或材料有变化处，应作为分段点；
③中间铰视为两个梁段间的联系，此种联系体现为两部分之间 的相互作用力，故应作为分段点；
(2)分段列出梁的挠曲线近似微分方程，并对其积分 两次
§6-2梁的挠曲线近似微分方程及其积分(精)

§6-2梁的挠曲线近似微分方程及其积分(精)


大挠度fmax和最大转角max。
解: 由对称性可知梁的两个支反力为
RA
q
RB
ql RA RB 2
A
B
x
y
l
例题 6 -2 图
此梁的弯矩方程及挠曲线微分方程分别为
ql 1 2 q M ( x) x qx (lx x 2 ) 2 2 2 q 2 EI ' ' M ( x) (lx x ) 2
EI ' ' M ( x) Pl Px (2)
例题 6-1 图
对挠曲线近似微分方程进行积分, 得
Px 2 EI ' Plx C1 (3) 2 Plx 2 Px 3 EI C1 x C 2 (4) 2 6
边界条件为 :
x
A
l x
B x
x 0, 0 x 0, ' 0
EIυ [ M ( x )dx ]dx C1x C2
得
C1 EI '| x 0 EI 0 C2 EI 0
式中，θ 0 和 v0 分别代表坐标原点处截面的转角和挠度。
例题６-３ 图示一抗弯刚度为EI的简支梁, 在D点处受一集中 力P的作用。试求此梁的挠曲线方程和转角方程，并求其最大 挠度和最大转角。
两段梁的挠曲线方程分别为
1 挠曲线方程 转角方程 挠度方程
( 0 «x «a)
2
( a«x « l )
b " P x EIv1 M1 l
b EIv2 " M 2 P x P( x a) l
3 θA ql θ max θB 24 EI
x
q
第四章(弯曲挠度3-Lu)

第四章(弯曲挠度3-Lu)

§4-9 用积分法计算梁旳挠度与转角
对于等截面梁，EI = 常数。
E I w "= - M (x)
EIw EI M ( x )dx C
EIw [ M (x)dx]dx Cx D
式中C, D 由梁支座处旳已知位移条件即位 移边界条件拟定。
HOHAI UNIVERSITY
EIw EI M ( x )dx C
C wc2(q)
c 2 (q)
HOHAI UNIVERSITY
3o 求 c、wc
A
c c (F ) c1(q) c2 (q)
F
C (F)
C (F )
B
C
qa 3 qa 3 qa 3
4 EI 6 EI 3EI
qa 3 4 EI
（b）
q
B
（d）
C
wc1(q) c1 (q )
wc wc (F ) wc1(q) wc2 (q)
EI 2
Fb 2l
x2
F 2
(
x
a
)2
C2
EIw2
Fb 6l
x3
F 6
(x
a)3
C2 x
D2
HOHAI UNIVERSITY
F
边界条件：x = 0 ，w1= 0。 x = l ，w2= 0。
a
b
A
CD
Bx
x
y
l
连续条件：x = a ，w1′= w2′， w1= w2
由连续条件，得：C1= C2， D1= D2
EIw [ M ( x)dx]dx Cx D
如：
p
A
B
p A
边界条件： wA=0 wB=0
边界条件： wA=0 θA=0
用积分法求梁的挠和转角

用积分法求梁的挠和转角

§8-3 用积分法求梁的挠度和转角 梁的挠曲线近似微分方程：
d2y dx 2
M (x) EI
EI
d2y dx2
M
(x)
积分一次得转角方程为：
EIy M (x)
dy dx
M (x) EI
dx
C
再积分一次得挠度方程为：
y
M (x) EI
dx
dx
Cx
D
§8-3 用积分法求梁的挠度和转角
梁截面的已知位移条件或位移约束条件，称为梁位移的边界条件。 积分常数C、D 由梁的位移边界条件和光滑连续条件确定。
5ql 4
ymax
y
x l 2
384EI
max
A
B
ql3 24 EI
§8-3 用积分法求梁的挠度和转角 外伸梁，承受集中载荷作用，试绘制挠曲线的大致形状图。
设弯矩刚度EI为常数。
§8-3 用积分法求梁的挠度和转角
解：1、绘制挠曲线的基本依据
1 y M (x)
(x)
EI z
根据弯矩的正、负、零值点或零值区，确定挠曲线的凹、
凸、拐点或直线区。
在梁的被约束处，应满足位移边界条件；在分段处，则 应满足位移连续条件。
§8-3 用积分法求梁的挠度和转角
三、使用视频 1.可使用的视频文件类型 常用格式为AVI,另一种为RealAudio。 2.加入视频 1）定位光标 2）选择“插入/图片/视频”菜单命令，弹出
“视频”对话框 3）选择视频文件 3.修改视频属性 1）选定视频位置上出现的图片 2）单击右键选择“图片属性” 3）在“图片属性”对话框中设置视频的属性
C ql3 24
EIy ql x3 q x4 Cx D 12 24
第十三讲：第九章 梁的弯曲-变形刚度计算概要

第十三讲：第九章 梁的弯曲-变形刚度计算概要


例11
求图示梁的挠曲线方程和转角方程。EI为常量。
Me A
x
e
解：
1.列微分方程并积分
B
M e Me x e M e FAy= M M EIy xx M l l l Me 2 EIy x Me x C 2l Me 3 Me 2 EIy x x Cx D 6l 2
33 5 Fl Fl Fl 2 l 6EI EI 2 EI 3
五、 叠加法求梁的变形
基本原理 由几个外力同时作用时所引起的梁的变形 转角和挠度 等于
由各个外力单独作用时所引起的梁的变形的代数和
q F M
e
y yq y F y M e
例13 求B和yB 解： 1. Me单独作用时 2Mel BM e EI 2 2 2 M l M 2 l e y BM e e EI 2 EI 2. F单独作用时 2 Fl BF CF 2 EI yBF yCF CF l
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
C'
y
1'
1
y f ( x)
——挠曲线方程
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x

y
1'
y
C'
1
在小变形下： 即：
dy y tan dx
——转角方程
任一横截面的转角 = 挠曲线在该截面形心处切线的斜率
2.数学方面
A
材料力学 积分法求梁的变形

材料力学 积分法求梁的变形

一、挠曲线近似微分方程
M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段，共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点： A = 0, q A = 0
B 点 ： w B 左 = w B 右
C点 ： w C左 = w C右
D点：w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
材料力学(土木类)第五章 梁弯曲时的位移(2)

材料力学(土木类)第五章 梁弯曲时的位移(2)

逆时针） （逆时针）
3 3 3
利用叠加原理求图示弯曲刚度为EI的悬臂梁 例5-6 利用叠加原理求图示弯曲刚度为 的悬臂梁 自由端B截面的挠度和转角 截面的挠度和转角。 自由端 截面的挠度和转角。
F A l C EI l F D l B
原荷载可看成为图a和 两种荷载的叠加 两种荷载的叠加， 解：原荷载可看成为图 和 b两种荷载的叠加，对应 的变形和相关量如图所示。 的变形和相关量如图所示。
Fl θ C1 = 2 EI
2
3
由位移关系可得此时B截面的挠度和转角为： 由位移关系可得此时 截面的挠度和转角为： 截面的挠度和转角为
Fl 3 Fl 2 4 Fl 3 wB1 = wC1 + θ C1 ⋅ BC = + × 2l = 向下） （向下） 3EI 2 EI 3EI Fl θ B1 = θ C1 = 2 EI
q ( x) x 2 dθ B = dθ ( x) = dx 2 EI
范围对q(x)dx的作用进行叠加，相当于 的作用进行叠加， 在x=0, l范围对 范围对 的作用进行叠加 对上两式在前述范围内积分， 对上两式在前述范围内积分，即：
wB = ∫ d wB = ∫
0
l
l
0
11q 0 l q ( x ) x (3l − x ) dx = 6 EI 120 EI
上次课回顾： 上次课回顾：
1、度量梁变形的两个基本位移量：挠度和转角 度量梁变形的两个基本位移量： 2、挠曲线近似微分方程
EIw′′ = − M ( x )
3、挠曲线近似微分方程的积分 、
EIw ' ( x ) = ∫ ( − M ( x )) dx + C1
EIw ( x ) =
梁的挠曲线近似微分方程

梁的挠曲线近似微分方程


由边界条件：
x 0，yA 0 ; D 0
xl,
yB 0 ;
C ql3 24
q
A
x θA
θB
y
l
B
x
EIy ql x3 q x4 Cx D 12 24
EIy ql x2 q x3 ql3 4 6 24
q (l3 6lx2 4x3)
ql x3 q x4 ql3 x 12 24 24
24EI
最大转角和最大挠度分别为：
y qx (l3 2lx2 x3) 24EI
ymax
y
x l 2
5ql 4 384EI
max
A
B
ql3 24 EI
外伸梁，承受集中载荷作用，试绘制挠曲线的大致形状图。 设弯矩刚度EI为常数。
§6-3 用积分法求梁的变形
解：1、绘制挠曲线的基本依据
1 y M (x)
(x)
EI z
根据弯矩的正、负、零值点或零值区，确定挠曲线的凹、
凸、拐点或直线区。
在梁的被约束处，应满足位移边界条件；在分段处，则 应满足位移连续条件。
载荷作用。试求此梁的转角方程和挠度方程，并确定最大转角
和最大挠度。
y
q
解：
FRA
FRB
ql 2
A
B
x
M(x) ql x q x2 22
x
l
EIy ql x q x2 22
EIy ql x2 q x3 C 46
EIy ql x3 q x4 Cx D 12 24
§6-3 用积分法求梁的变形
§6-3 用积分法求梁的变形
梁的挠曲线近似微分方程：
d 2 y M (x) dx2 EI
梁的变形

梁的变形

1 2 1 3 C1 PL ; C 2 PL 2 6
2
写出挠曲线方程和转角方程，并画出挠曲线
P v( x ) ( L x )3 3 L2 x L3 6 EI P q ( x ) v' ( L x )2 L2 2 EI
最大挠度及最大转角


v
P L
度量梁变形的两个基本量
1.挠度：横截面形心沿垂直于轴线方向的线位移。用v 表示。
v向下为正，反之为负。
2.转角：横截面绕其中性轴转动的角度。用q 表示， 顺时针转动为正，反之为负。
C v v
q
P x
C’
转角与挠度的关系
挠曲线上任一点的纵坐标 v（x）即为该点的
横截面的挠度。
dv tgq v' dx
qmax
x


vmax
PL3 v ( L) ( ) 3 EI
q max
PL2 q ( L) ( ) 2 EI
例： 简支梁受集中力F作用，求梁的转角方程和挠度方程， 并求C截面的挠度和A截面的转角。已知梁的EI，l=a+b，a>b。 解：1）由梁整体平衡分析得： HA
H A 0, RA Fb Fa , RB l l
前面讨论了(梁）弯曲 内力、弯曲应力，接下
来讨论弯曲变形。
第10章
梁的变形
梁在外力作用下除了限制其应力，使其满 足强度条件外，还必须限制它的变形，即必须 具有足够的刚度，满足刚度条件。 例如：楼板弯曲变形太大.则平顶下面的粉 刷层就会剥落，不但影响美观，而且给人以不 安全的感觉；高速铁路桥梁变形过大，就无法 提高行车速度。
2、尽量减小梁的跨度或长度，减少弯矩数值

用积分法求梁的挠度和转角

梁的挠曲线近似微分方程：
d 2 y M (x) dx2 EI
EI
d2y dx2
M
(x)
积分一次得转角方程为：
EIy M (x)
dy dx

M (x) EI
dx
C
再积分一次得挠度方程为：
y
M (x) EI
dx
dx
Cx
D
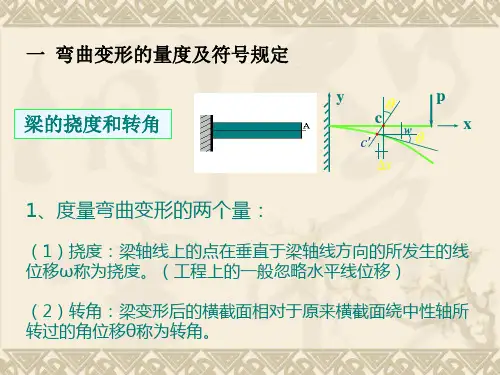
梁截面的已知位移条件或位移约束条件，称为梁位移的边界条件。 积分常数C、D 由梁的位移边界条件和光滑连续条件确定。
EIy ql x3 q x4 Cx D 12 24
由边界条件：
x 0，yA 0 ; D 0
xl,
yB 0 ;
C ql3 24
例8-2 一简支梁如图8-9所示，在全梁上受集度为q的均布载荷作用 。试求此梁的转角方程和挠度方程，并确定最大转角和最大挠度。
x 0，yA 0 ; D 0
dx EI 2
再积分一次
y
F
lx 2 (
x3 ) Cx D
EI 2 6
2、由位移边界条件确定积分常数
x 0, A 0
x 0, yA 0
代入求解
C 0, D 0
3、确定转角方程和挠度方程
F (lx x2 ) y F (lx2 x3 )
EI 2
EI 2 6
4、确定最大转角和最大挠度
24EI
最大转角和最大挠度分别为：
5ql 4
ymax
y
x l 2
384EI
max
A
B
ql3 24 EI
感谢下 载
xl,
yB 0 ;
C ql3 24
EIy ql x3 q x4 Cx D 12 24

挠曲线的近似微分方程


Bx FBy
解：弯矩方程 :
M x 1 qlx 1 qx2
22
挠曲线的近似微分方程:
w

1 EI z

1 2
qlx

1 2
qx2

进行一次积分得：
w

1 EI z

1 4
qlx2

1 6
qx3
C

再进行第二次积分得：
w

1 EI z
1 12
qlx3
Tmax 180 [] GIp
一般传动轴， [φ’] = 0.5 ~1/m
例4 图为一圆截面轴 AC ，受扭转力偶矩MA，MB 与Mc作用。 已知MA =90 N·m , MB =160 N·m ， MC =70 N·m ， l=2 m， G=80 GPa ， IP=3.0×105 mm4 ， [φ’] =0.3 (o)/m 。试计算 该轴的总扭转角 φAC （即截面C对截面A的相对转角），并 校核轴的刚度。
F C、D为积分常数，它由位移边界与连续条件确定。
边界条件：梁截面的已知位移条件 固定端的挠度和转角均为零，铰支座处的挠度为零。
A
wA=0 θA=0
F B
A wA=0
F C
B
wC1=wC2 wB=0 θC1=θC2
$ 挠曲轴在C点连续且光滑 连续条件：分段处挠曲轴应满足的连续、光滑条件
例6 如图所示图形为一外伸梁，承受集中载荷作用，试绘制
B
w xl
ql3 6EI z
ql 4
wB
w xl
8EI z
根据挠度和转角的符号规定，上述结果表明转角为顺时针，挠度方 向为向下。

概述梁的挠曲线近似微分方程及其积分用积分


1
( x)
d 2w dx2
dx
y
M<0
d2w dx2
M (x) EI
d2w dx2
0
x
o
d2w dx2
M (x)(2) EI
式（2）就是挠曲线近似微分方程。
对于等截面直梁，挠曲线近似微分方程可写成如下形式：
d2w dx2
M (x) EI
EI
d2w dx2
M
(x)
二、求转角方程、挠曲线方程 1.微分方程的积分
y
a
P
A x1
C
x2
L
x B
EIw
0
P(a
x1)
(0 x1 a) (a x2 L)
EIw
P 2
x12
Pax1
C1
C2
EIw
P
6
x13
Pa 2
x12
C1x1
D1
C2 x2 D2
确定积分常数 边界条件
EI 0 x1 0
EI w 0 x1 0
C1 0 D1 0
连续性条件
当 x1 x2 a 时，
题一、解：
x
y
L
P
建立坐标系并写出弯矩方程
A
B
M (x) P(L x)
x
写出挠曲线微分方程并积分
EIw M (x) P(L x)
EIw P x2 PLx C 2
EIw P x3 PL x2 Cx D 62
确定积分常数
当 x 0 时，
A wA 0， wA 0
求得：
C 0; D 0
(6a
a)
RC a3 3EI
a
RC a
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

可见该梁的qmax和wmax均在x=l的自由端处。于是有
qmax
q
|xl
Fl 2 EI

Fl 2 2EI

Fl 2 2EI


wmax

w
|xl

Fl 3 2EI
Fl 3 6EI
Fl 3 3EI

由此题可见，当以x为自变量对挠曲线近似微分方程 进行积分时，所得转角方程和挠曲线方程中的积分常数 是有其几何意义的：
从几何方面来看，平面曲线的曲率可写作
1
w
x 1 w2 3/2
式中，等号右边有正负号是因为曲率1/为度量平面曲线 (挠曲线)弯曲变形程度的非负值的量，而w"是q = w' 沿x方
向的变化率，是有正负的。
再注意到在图示坐标系中，负弯矩对应于正值w" ，正弯矩对
应于负值的w" ，故从上列两式应有
22
2
挠曲线近似微分方程为
EIw M x q lx x2 2 以x为自变量进行积分得：
EIw


q 2

lx2 2

x3 3


C1
EIw

q 2

lx3 6

x4 12
转角则明显不同。
在图示坐标系中，挠度w向下为正，向上为负；
顺时针转向的转角q为正，逆时针转向的转角q为负。
§5-2 梁的挠曲线近似微分方程及其积分
Ⅰ. 挠曲线近似微分方程的导出 在§4-4中曾得到等直梁在线弹性范围内纯弯曲情况
下中性层的曲率为
1M EI
这也就是位于中性层内的挠曲线的曲率的表达式。
F
lx2 2

x3 6

C1x

C2
该梁的边界条件为：在 x=0 处 w 0，w =0
于是得
C1 0，C2 0
从而有 转角方程 q w Fxl Fx2
EI 2EI 挠曲线方程 w Fx2l Fx3
2EI 6EI 根据该梁边界条件和全梁横截面上弯矩均为负值， 以及挠曲线应光滑连续描出了挠曲线的示意图。
w
M x
1 w2 3/2 EI
由于梁的挠曲线为一平坦的曲线，上式中的w2与1相比可略
去，于是得挠曲线近似微分方程 w M x
EI
Ⅱ. 挠曲线近似微分方程的积分及边界条件
w M x
EI 求等直梁的挠曲线方程时可将上式改写为
EIw M x
横截面的转角q 也就是挠曲线在该相应点的切线与x轴之
间的夹角，从而有转角方程：
q tanq w f x
(a)
(b)
直梁弯曲时的挠度和转角这两个位移不但与梁的弯曲
变形程度(挠曲线曲率的大小)有关，也与支座约束的条件
有关。图a和图b所示两根梁，如果它们的材料和尺寸相同， 所受的外力偶之矩Me也相等，显然它们的变形程度(也就 是挠曲线的曲率大小)相同，但两根梁相应截面的挠度和
后进行积分，再利用边界条件(boundary condition)确定积分 常数。
当全梁各横截面上的弯矩 可用一个弯矩方程表示时(例如 图中所示情况)有
EIw M xd x C1
EIw M xd x d x C1x C2
以上两式中的积分常数C1， C2由边界条件确定后即可得出梁 的转角方程和挠曲线方程。
边界条件(这里也就是支座处的约束条件)的示例如 下图所示。
若由于梁上的荷载不连续等原因使得梁的弯矩方程 需分段写出时，各段梁的挠曲线近似微分方程也就不同。 而对各段梁的近似微分方程积分时，都将出现两个积分 常数。要确定这些积分常数，除利用支座处的约束条件 (constraint condition)外，还需利用相邻两段梁在交界处 的连续条件(continuity condition)。这两类条件统称为边 界条件。
§5-1 梁的位移——挠度和转角
直梁在对称平面xy内弯曲时其原来的轴线AB将弯曲成 平面曲线AC1B。梁的横截面形心(即轴线AB上的点)在垂直 于x轴方向的线位移w称为挠度(deflection)，横截面对其原
来位置的角位移q 称为横截面的转角(angle of rotation)。
弯曲后梁的轴线——挠曲线(deflection curve)为一平 坦而光滑的曲线，它可以表达为w=f(x)，此式称为挠曲线 方程。由于梁变形后的横截面仍与挠曲线保持垂直，故
在横力弯曲下，梁的横截面上除弯矩M=M(x)外，还 有剪力FS=FS(x)，剪力产生的剪切变形对梁的变形也会产 生影响。但工程上常用的梁其跨长l 往往大于横截面高度h 的10倍，此时剪力FS对梁的变形的影响可略去不计，而有
x
1
x

M x
EI
注意：对于有些l/h>10的梁，例如工字形截面等直梁，如同 在核电站中会遇到的那样，梁的翼缘由不锈钢制作，而主 要承受剪力的腹板则由价廉但切变模量较小的复合材料制 作，此时剪切变形对梁的变形的影响是不可忽略的。
C2 EIw |x0 EIw0
思考: 试求图示等截面悬臂梁在所示坐标系中的挠曲线 方程和转角方程。积分常数C1和C2等于零吗？
例题5-2 试求图示等直梁的挠曲线方程和转角方程，
并确定其最大挠度wmax和最大转角qmax。
解：该梁的弯矩方程为
M x ql x 1 qx2 q lx x2
C1 EIw |x0 EIq0
C2 EIw |x0 EIw0
此例题所示的悬臂梁，q0=0，w0=0， 因而也有C1=0 ，C2=0。
事实上，当以x为自变量时
EIw M xd x C1 EIw [[M xd x]d x C1x C2
两式中的积分在坐标原点处(即x=0处)总是等于零，从而有 C1 EIw |x0 EIq0
例题5-1 试求图示等直梁的挠曲线方程和转角方程，
并确定其最大挠度wmax和最大转角qmax。
解：该梁的弯矩方程为
M x Fl x
挠曲线近似微分方程为
EIw M x Fl x
以x为自变量进行积分得
EIw

F lx

x2 2
Hale Waihona Puke C1EIw