材料力学A_(梁弯曲变形的描述,挠曲线近似微分方程,积分法和.

10.2 梁的挠曲线近似微分方程及其积分纯弯曲 EIM =ρ1挠曲线曲率()322"1w w κ=⎡⎤'+⎣⎦EIM ±=d θFFxd xyxρ O正负号的确定xyOxyOM > 0w ″< 0M < 0w ″>0M 与 w ″异号()322"1w w κ=⎡⎤'+⎣⎦EIM ±=()3221w M EIw ''=-⎡⎤'+⎣⎦小变形：转角 w ′ ≈ 0 适用条件： 1. 坐标系，正负号；2. 忽略剪力 F S 对变形的影响；3. 线弹性，小变形，w′ ≈ 0。

M w EI''=-EI ——梁的抗弯刚度， 若为等直梁，EI ＝C ，则 EIw M''=-挠曲线近似微分方程1'd Mw x C EIθ==-+⎰12d d M w x x C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰一次积分：二次积分：积分法计算梁的变形BAlw A = 0 w B = 0BAlw A = 0 θA =0EIw M''=-挠曲线近似微分方程 由边界条件，确定积分常数光滑连续条件——相邻挠曲线必须光滑连续。

挠曲线近似微分方程及其积分w C2= w C3θC2=θC2w B1= w B2θB1=θB2挠曲线近似微分方程及其积分——例题[例题1] 已知悬臂梁的抗弯刚度为EI，求在荷载P 作用下梁的挠曲线方程，并确定梁上的最大挠度和转角。

BAxL P有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）[解] （1）建立弯矩方程 ()()M x P L x =-()()E Iw M x P L x ''=-=--21()2xEIw P Lx C '=--+2312()26Lx x EIw P C x C =--++（3）确定积分常数 0,0x w ==0,0x w '==20C=10C=挠曲线近似微分方程及其积分——例题BALxPx（2）代入挠曲线方程并积分挠曲线近似微分方程222PLx Pxw EIθ-'==-23(3)6P Lx x w EI-=-最大挠度和转角3max()3PL f EI=↑2max2PL EIθ=挠曲线近似微分方程及其积分——例题B ALxPxmaxθmaxw挠曲线近似微分方程及其积分——例题[例题2] 已知：EI = 常数，求：1. 挠度、转角方程； 2. |θmax |, |w max |。

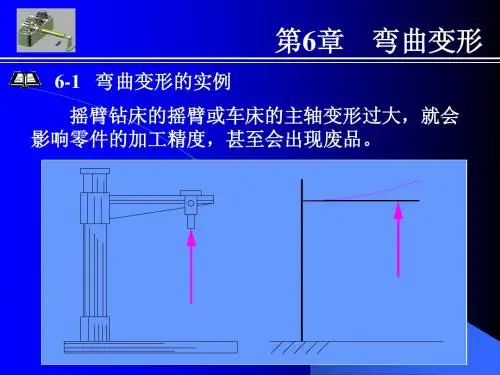
第六章弯曲变形知识要点1、弯曲变形的概念1）、挠曲线弯曲变形后梁的轴线变为挠曲线。

平面弯曲时，挠曲线为外力作用平面内的平面曲线。

2）、平面弯曲时的变形在小变形情况下，梁的任意二横截面绕各自的中性轴作相对转动，杆件的轴线变为平面曲线，其变形程度以挠曲线的曲率来度量。

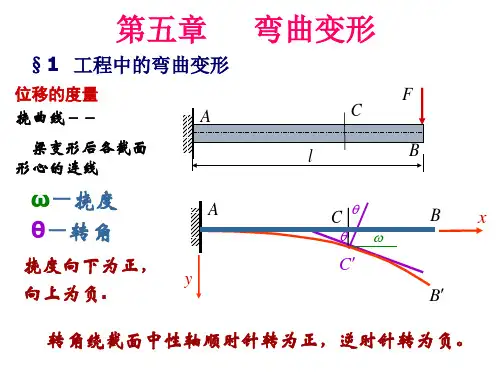
1》纯弯曲时，弯矩—曲率的关系（由上式看出，若弯曲刚度EI为常数则曲率为常数，即挠曲线为圆弧线）2》横力弯曲时，弯矩—曲率的关系3）、平面弯曲时的位移1》挠度——横截面形心在垂直于梁轴线方向上的线位移，以表示。

2》转角——横截面绕其中性轴旋转的角位移，以表示。

挠度和转角的正负号由所选坐标系的正方向来确定。

沿y轴正方向的挠度为正。

转角的正负号判定规则为，将x轴绕原点旋转90°而与y轴重合，若转角与它的转向相同，则为正，反之为负。

4）、挠曲线近似微分方程5）、受弯曲构件的刚度条件，2、积分法求梁的挠度和转角由积分常数C、D由边界条件和连续性条件确定。

对于梁上有突变载荷（集中力、集中力偶、间断性分布力）的情况，梁的弯矩M(x)不是光滑连续函数，应用上式时，应分段积分，每分一段就多出现两个积分常数。

因此除了用边界条件外，还要用连续性条件确定所有的积分常数。

边界条件：支座对梁的位移（挠度和转角）的约束条件。

连续条件：挠曲线的光滑连续条件。

悬臂梁边界条件：固定端挠度为0，转角为0连续条件：在载荷分界处（控制截面处）左右两边挠度相等，转角相等简支梁边界条件：固定绞支座或滑动绞支座处挠度为0连续条件：在载荷分界处（控制截面处）左右两边挠度相等，转角相等连接铰链处，左右两端挠度相等，转角不等3、叠加原理求梁的挠度和转角1）、叠加原理各载荷同时作用下梁任一截面的挠度和转角等于各个载荷单独作用时同一截面挠度和转角的代数和。

2）、叠加原理的限制叠加原理要求梁某个截面的挠度和转角与该截面的弯矩成线性关系，因此要求：1》弯矩M和曲率成线性关系，这就要求材料是线弹性材料2》曲率与挠度成线性关系，这就要求梁变形为小变形4、弯曲时的超静定问题——超静定梁1）、超静定梁约束反力数目多于可应用的独立的静力平衡方程数的梁称为超静定梁，它的未知力不能用静力平衡方程完全确定，必须由变形相容条件和力与变形间的物理关系建立补充方程，然后联立静力平衡方程与补充方程，求解所有的未知数。