下载文档原格式
主要内容及重点：计算弯曲变形的积分法、叠加法弯曲刚度计算梁的超静定问题1.弯曲变形工程中的弯曲变形问题2.1、挠曲线OB—平面弯曲时，梁变形后轴线。
在xoy 平面内的一条连续、光滑的弹性曲线。
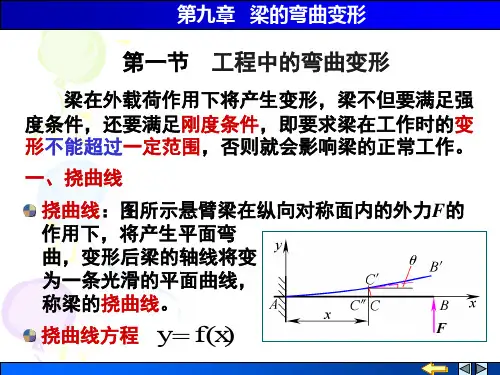
PyxBA（梁弯曲变形的两个基本量）（1）挠度：梁变形后，横截面的形心在垂直于梁轴线（x 轴）方向上所产生的线位移，称为梁在截面的挠度。
一般情况下，不同横截面的挠度值不同。
横截面挠度随截面位置（x 轴）而改变的规律用挠曲线方程表示。
即：）（x f y =y AP x由梁弯曲的平面假设可知：梁的横截面变形前垂直于轴线，变形后仍垂直于挠曲线。
：曲线OAB 在A 点的切线与X 轴间的夹角θABAy AP xθA）挠度与转角的关系挠曲线切线的斜率：θtg dxdy=工程中θ极小：θθtg ≈)(x f dy′==θzEI M ＝ρ1zEI x M x )()(1＝ρOBPyxBPx23222])d d (1[d d )(1xw x w x +±＝ρz EI x M xw x w)(])d d (1d d 23222=+zEI x )(ρzEI x M x w )(d d 22＝±zEI x M x w )(d d 22＝±o>0d 2M>0d 2d 2<0oM<02d zEI Mx w ＝22d d －挠曲线近似微分方程线弹性范围适用对于等直梁)(x M x w EI z =22d d Cx x M xwEI x EI z z +=∫d )(d d )(＝θDCx x x x M x w EI z ++=∫∫d d )()(C 、D ：积分常数边界条件已知的挠度及转角光滑连续性PM(x)＝F P (L-x)xF L F x L x M xwP P 22))(d −=−=DCx x F x F ++−=3P 2P 6121)θA ＝0 x ＝0 时w A ＝0C=0 D=0)()(x L EI xF x z −22P ＝θ)3(6)(2P x L EI xF w z−＝θEI LF 22P max ＝θL F w 3P ＝Pmaxm a xθC x F Lx F x EI P Z +−==2P 21)(θmaxy maxB θ解：建立坐标、写弯矩方程）段：（20lx AC <≤）段：（l x lCB ≤<2BCL/2L/2xxPxx 21)(=)2(21)(lx P Px x M −−=Px1)=)(1)(lx P Px x y EI −−=′′一次：利用边界条件确定积分常数：12141C Px EI Z +=θ1131121D x C Px y EI Z ++=2222)2(241C l x P Px EI Z +−−=θ22332)2(6121D x C l x P Px y EI Z ++−−=⇒==右左右左，C C C C y y θθ2121DDC C ==2100D D y x A =⇒==，02Pl C C y l x B −==⇒==，maxy maxB θBCpL/2164Z 224EI Z )1612(23x Pl Px Z −]16)2(6121[12332x Pl l x P Px EI y Z −−−=max0θ，，l x ==ZEIPl 162max∓=θmax2y lx ，=ZEIPl y 483max−=maxy maxB θBCpx思考：在用积分法求梁的转角和位移过程中，何时需要考虑静力关系、物理关系、变形协调关系？静力关系：支反力、弯矩计算物理关系：挠曲线近似微分方程变形协调关系：积分运算及边界条件图示纯弯曲悬臂梁的挠曲线应为一圆弧线，而由积分法求得的梁挠曲线为二次抛物线为什么？近似微分方程获得的梁挠曲线近似解自由端B 处挠度的精确解：EIxM v e 22=()+−=⎟⎟⎠⎞⎜⎜⎝⎛+−=−=43242!4!2cos 1lM l M v e e BBB θθρθρ1222211)()()(a x m x Lm x M x L mx M −−＝＝2a a 2a x2()2)(452)(2)(222222211a x q a x qa x q x M x q x M −+−+−−＝＝5.用叠加法求弯曲变形叠加法：当梁上同时作用几个荷载时，在小变形情况下，且梁内应力不超过比例极限，则每个荷载所引起的变形（挠度和转角）将不受其它荷载的影响。
