当前位置：文档之家 › 9.5 梁的位移与挠曲线近似微分方程

9.5 梁的位移与挠曲线近似微分方程

  • 格式：ppt
  • 大小：1.20 MB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

梁的挠曲线近似微分方程及其积分.

梁的挠曲线近似微分方程及其积分.

f (P1P2 Pn ) f1(P1 ) f2 (P2 ) fn (Pn )
二、结构形式叠加（逐段刚化法）：
A a
P q
C a
P
a
a
q
a
a
+
=
例6－4-1 按叠加原理求A点转角 和C点挠度.
解、载荷分解如图
、由梁的简单载荷变形表，
查简单载荷引起的变形。
PA
Pa 2 4 EI
f ( x) M ( x) I0 M ( x)
EI ( x) I0
EI 0
EI 0 f ( x) M ( x)
M(x) M(x) I0
I(x)
：几何形状：长度不变，惯性矩变为I0 。
：实梁对应方程： EI0 f ( x) M ( x)
虚梁对应方程：
M (x) q(x)
：令：q(x) M ( x ) 依此建立虚梁上的分布载荷。
8
2
- q a2
a2
C
a
求虚梁B点的剪力和弯矩
x
13qa 3 RA 72
QB
13qa3 72
1 2
qa2 2
a
5 72
qa3
MB
13qa3 72
a
1 2
qa2 2
a
a 3
7 72
qa4
D
B
5qa 3 72EI
7qa4 f B 72EI
C点左右位移怎样？
四、变截面直梁的共轭梁法： ：将截面的变化折算到弯矩之中去。
梁的挠曲线微分:方E程 If ( x) M ( x) 梁的外载与内力的为关 : M系(x) q(x)
上二式形式相同，用类比法，将微分方程从形式上转化为 外载与内力的关系方程。从而把求挠度与转角的问题转化为求 弯矩与剪力的问题。
概述梁的挠曲线近似微分方程及其积分用积分

概述梁的挠曲线近似微分方程及其积分用积分


x 0 时， ， wA 0 A w A 0
当
求得：
C 0; D 0
y
L
P
B
B
wB
x
写出挠曲线方程并画出挠曲线的大致形状
Px 2 w( x) ( x 3L) 6EI
最大转角及最大挠度（绝对值最大）
max
PL2 B （ ） 2 EI
wmax
PL3 wB （ ） 3EI
C
x1
x2
AB段 (0 x1 a)
a
a
M1 Px1
BC段 (0 x2 a)
M 2 P(a x2 )
写出挠曲线微分方程并积分 AB段
M1 Px1 EIw1
P 2 EI1 x1 C1 EIw1 2 P 3 EIw x1 C1 x1 D1 6
1
y
M<0
d2w 0 2 dx
d2w M ( x) 2 EI dx
o
x
d 2 w M ( x) (2) 2 EI dx
式（2）就是挠曲线近似微分方程。
对于等截面直梁，挠曲线近似微分方程可写成如下形式：
d w M ( x) 2 EI dx
二、求转角方程、挠曲线方程 1.微分方程的积分
最大挠度及最大转角
dw( x 2 ) Pa 2 ( x2 ) dx 2 2 EI
2
y
a
P
C
C
max C CB
wmax
Pa 2 2EI
L
B
x
wB
Pa 2 wB (3L a) 6EI
例2 求图示梁自由端的转角和挠度。
材料力学 梁 弯曲位移

材料力学 梁 弯曲位移


D点的连续条件： x = a， 1' 2 ' 1 2
1 ( 0 x a)
2 (axl )
挠曲线方程
EI
1"
M1
F
b l
x
EI
2"
M
2
F
b l
x
F
(
x
a)
转角方程
EI
'
1
F b l
x2 2
C1
EI
2'
F
b l
x2 2
F
(
xa)2 2
D1
挠度方程
EI
1
F
b l
x3 6
C1 x
C2
EI
2
F
b l
式中：积分常数 C1 、C2 可通过梁挠曲线的 边界条件 和 变形 连续性条件 来确定。
1、边界条件
A
l A= 0
B
B= 0
A
A= 0
B
B= 0
在简支梁或外伸梁中， 铰支座处的挠度 都应等于零。
A 0 B 0
A
B
l A= 0 A= 0
在悬臂梁 中，固定端处的挠度 和转角 都应等于零。
A 0, A 0
F
(
xa)2 2
D1
挠度方程
EI
1
F
b l
x3 6
C1 x
C2
EI
2
F
b l
x3 6
F
(x 6
a)3
D1
x
D2
x = 0 ， 1 = 0
x = l ， 2= 0
再将边界条件代入方程可解得:
讲梁的挠曲线方程与积分解法

讲梁的挠曲线方程与积分解法


②积分常数的确定——边界条件和连续条件：
边界条件：梁在其支承处的挠度或转角是已知的， 这样的已知条件称为边界条件。 连续条件：梁的挠曲线是一条连续、光滑、平坦 的曲线。因此，在梁的同一截面上不可能有两个 不同的挠度值或转角值，这样的已知条件称为连 续条件。
边界条件
积分常数2n个=2n个
连续条件
列出图示结构的边界条件和连续条件。
8
代入（1）（2）得：
1 ( 1 qx3 1 qL3)
EI 6 6
1 ( 1 qx4 qL3 x qL4 )
EI 24
68
将 x 0 代入得：
A
qL3 6EI
（与C比较知E：I A C）
A
qL4 8EI
（与D比较知E：IA ）D
因此
常数C表示起始截面的转角×刚度(EI)
常数D表示起始截面的挠度×刚度(EI)
x L
2
2、
d 2
dx 2
M (x) EI z
EI" 1 qx2
2
积分一次： EI' EI 1 qx3 C （1）
积分二次：
6
EI 1 qx4 Cx D （2）
24
B X``
3、确定常数C、D.
由边界条件： x L, 0 代入（1）得： C 1 qL3
6
x L, y 0 代入（2）得： D 1 qL4
支座反力，分段列弯矩方程； 分段的原则:
①凡载荷有突变处（包括中间支座），应作为分段点；
②凡截面有变化处，或材料有变化处，应作为分段点；
③中间铰视为两个梁段间的联系，此种联系体现为两部分之间 的相互作用力，故应作为分段点；
(2)分段列出梁的挠曲线近似微分方程，并对其积分 两次
10-1 梁挠曲线的近似微分方程

10-1 梁挠曲线的近似微分方程

1
第十章
§10–1
目录
梁的弯曲变形
梁挠曲线的近似微分方程
§10–2 用积分求梁的变形 §10–3 叠加法求梁的变形 §10–4 梁的刚度计算和提高梁刚度的措施
2
教学内容： • 梁的挠曲线近似微分方程、转角和位移、边界 条件和连续条件的概念。 教学要求： • 1、理解梁变形的两个基本量（挠度和转角） • 2、掌握梁的挠曲线近似微分方程； • 重点：梁的挠曲线近似微分方程。 • 学时安排：1
P 2
P 2
P
7
§10–1 梁挠曲线的近似微分方程
三、弯曲变形的度量
1、梁的变形： 梁承载前后形状的变化称为变形，一般用各段梁曲率的变 化表示。 2、梁的位移： 梁变形前后位置的变化称为位移，位移包括线位移和角位移。 P y x
3、挠曲线: v=f(x)
f(x)
纵向对称面上，作用横向力，变形后，轴线由原来的 直线变成曲线，为纵向对称面内的一条光滑的曲线，称为 挠曲线 。
1 v ( x) [1 (v) 2 ]3/2
1 v ( x)
y M(x)>0
d v dx2
2
在小变形时，梁的挠曲线是 一条平缓的曲线，转角 v ' tan 的数值很小，可忽略不计。 弯矩M与挠曲线曲率 v 的值 总是异号的。 y M(x)<0
d 2v dx
2
M x v EI
x
x
0 (v 0)
0 (v 0)
M x v EI
挠曲线的近似微分方程
11
挠曲线的近似微分方程
M ( x) v EI
EIv M ( x)
由上式进行积分，就可以求出梁横截面的转角方程和挠度方程
梁的弯曲-变形刚度计算

梁的弯曲-变形刚度计算


一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
C'
y
1'
1
Байду номын сангаас
y f ( x)
——挠曲线方程
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x

y
1'
y
C'
1
在小变形下： 即：
dy y tan dx
——转角方程
任一横截面的转角 = 挠曲线在该截面形心处切线的斜率
2
9 ql 2 128
M max
1 2 M A ql 8
例 14 试作图示超静定梁的剪力图和弯矩图。
q
5.讨论 设MA为多余约束力 列变形几何方程
A Aq AM 0
A
A l
B 原结构
q MA A B 静定基
查表
Aq
ql M Al ， AM A 24 EI 3 EI
5Fl 3 Fl 2 Fl 3 l 6 EI 3 EI 2 EI
F A l C l
Me B
yBM
A F A C B
e
BM
B
e
Me
BF
yBF
3. Me和F共同作用时
2 M e l Fl 2 B BM e BF EI 2 EI 2 M e l 2 5Fl 3 y B y BM e y BF EI 6 EI
2.确定积分常数
FBy=
l
Me l
由 y x 0 0, D 0
工程力学第1节 挠曲线近似微分方程

工程力学第1节 挠曲线近似微分方程


挠曲轴线 近似微分方程 结论
M ( x) y EI
两种情况下弯矩与曲线的二阶导数均同号，微分 方程式应取正号，即： 挠曲轴线 近似微分方程
M ( x) y EI
梁的挠曲轴线近似微分方程的适用条件：梁的变 形是线弹性的小变形。
M ( x) y EI
微分方程弯矩M与曲线的二阶导数 y的正负号关系
1）如图a所示，梁的挠曲轴线是一下凸曲线，梁的下 侧纤维受拉，弯矩 M >0，曲线的二阶导数 y >0；
2）如图b所示，梁的挠曲轴线是一上凸曲线，梁的下 侧纤维受压，弯矩 M <0，曲线的二阶导数 y <0；
第十章
梁的弯曲变形
一、挠曲轴线近似微分方程
挠曲轴线：图示悬臂 梁在纵向对称面内的 外力 F 的作用下，将 产生平面弯曲，变形 后梁的轴线将变为一 条光滑的平面曲线， 称梁的挠曲轴线。
挠曲轴线方程
y f ( x)
y f ( x)
挠度：截面形心线位移的垂直分量称为该截面的 挠度，用 y 表示。
第ቤተ መጻሕፍቲ ባይዱ章
梁的弯曲变形
工程中的很多结构或构件在工作时， 不但要满 足强度条件，同时对于弯曲变形都有一定的要求：
第一类是要求梁的位移不得超过一定的数值。例如 若机床主轴的变形过大，将会影响齿轮的正常啮合 以及轴与轴承的正常配合，造成不均匀磨损、振动 及噪音，缩短了机床的使用寿命，还影响机床的加 工精度。因此，在工程中进行梁的设计时，除了必 须满足强度条件之外，还必须限制梁的变形，使其 不超过许用的变形值。 第二类是要求构件能产生足量的变形。例如车辆钢 板弹簧，变形大可减缓车辆所受到的冲击；跳水起 跳板大变形，以确保运动员被弹起。
转角：横截面绕中性轴转动产生了角位移，此角 位移称转角，用 表示。小变形时，转角 很小， 则有以下关系：
材料力学(土木类)第五章 梁弯曲时的位移(2)

材料力学(土木类)第五章 梁弯曲时的位移(2)

逆时针） （逆时针）
3 3 3
利用叠加原理求图示弯曲刚度为EI的悬臂梁 例5-6 利用叠加原理求图示弯曲刚度为 的悬臂梁 自由端B截面的挠度和转角 截面的挠度和转角。 自由端 截面的挠度和转角。
F A l C EI l F D l B
原荷载可看成为图a和 两种荷载的叠加 两种荷载的叠加， 解：原荷载可看成为图 和 b两种荷载的叠加，对应 的变形和相关量如图所示。 的变形和相关量如图所示。
Fl θ C1 = 2 EI
2
3
由位移关系可得此时B截面的挠度和转角为： 由位移关系可得此时 截面的挠度和转角为： 截面的挠度和转角为
Fl 3 Fl 2 4 Fl 3 wB1 = wC1 + θ C1 ⋅ BC = + × 2l = 向下） （向下） 3EI 2 EI 3EI Fl θ B1 = θ C1 = 2 EI
q ( x) x 2 dθ B = dθ ( x) = dx 2 EI
范围对q(x)dx的作用进行叠加，相当于 的作用进行叠加， 在x=0, l范围对 范围对 的作用进行叠加 对上两式在前述范围内积分， 对上两式在前述范围内积分，即：
wB = ∫ d wB = ∫
0
l
l
0
11q 0 l q ( x ) x (3l − x ) dx = 6 EI 120 EI
上次课回顾： 上次课回顾：
1、度量梁变形的两个基本位移量：挠度和转角 度量梁变形的两个基本位移量： 2、挠曲线近似微分方程
EIw′′ = − M ( x )
3、挠曲线近似微分方程的积分 、
EIw ' ( x ) = ∫ ( − M ( x )) dx + C1
EIw ( x ) =
梁的挠曲线近似微分方程

梁的挠曲线近似微分方程


由边界条件：
x 0，yA 0 ; D 0
xl,
yB 0 ;
C ql3 24
q
A
x θA
θB
y
l
B
x
EIy ql x3 q x4 Cx D 12 24
EIy ql x2 q x3 ql3 4 6 24
q (l3 6lx2 4x3)
ql x3 q x4 ql3 x 12 24 24
24EI
最大转角和最大挠度分别为：
y qx (l3 2lx2 x3) 24EI
ymax
y
x l 2
5ql 4 384EI
max
A
B
ql3 24 EI
外伸梁，承受集中载荷作用，试绘制挠曲线的大致形状图。 设弯矩刚度EI为常数。
§6-3 用积分法求梁的变形
解：1、绘制挠曲线的基本依据
1 y M (x)
(x)
EI z
根据弯矩的正、负、零值点或零值区，确定挠曲线的凹、
凸、拐点或直线区。
在梁的被约束处，应满足位移边界条件；在分段处，则 应满足位移连续条件。
载荷作用。试求此梁的转角方程和挠度方程，并确定最大转角
和最大挠度。
y
q
解：
FRA
FRB
ql 2
A
B
x
M(x) ql x q x2 22
x
l
EIy ql x q x2 22
EIy ql x2 q x3 C 46
EIy ql x3 q x4 Cx D 12 24
§6-3 用积分法求梁的变形
§6-3 用积分法求梁的变形
梁的挠曲线近似微分方程：
d 2 y M (x) dx2 EI
梁位移

梁位移


EI z
2
y(x) 1 (1 Plx2 1 Plx3)
EI z 2
6
ymax

y(l)


1 EIz
(1 2
Pl3

1 6
Pl3)


Pl3 3EIz
()
max
(l)


1 EIz
(Pl2

1 2
Pl2)


Pl2（逆时针） 2EIz
9
例2：求此梁的转角方程和挠度方程，确定最大转角，挠度。
由于梁变形后横截面仍垂直于轴线，因此任一截面的转角，
也可用截面形心处挠曲线的切线与x轴的夹角来表示。
则有： (切线) dy(x) tg
dx
因很小，可写成 tg
(x) dy(x) y
dx
即：任一横截面的转角 等于该截面处挠度y 对x的一阶导数，只
要知道梁的挠曲线方程，则可确定任一点的挠度和截面的转角。
分布力等时， 应该分段积分。每一个分段中都有两个积分常数，
它们要满足连续变形条件。
7
例1：9.1 求挠度方程和转角方程，并确定最大值。
解：确定支座反力：
RA P MA Pl
弯矩方程：
M (x) Pl Px
挠度、转角方程：
EIz (x) (Pl Px)dx C
因分段（x=a）处曲线连续变形，
y11
(a) (a)

y2
2
(a) (a)

C1

C2

Pb 6l
(b2

l2)
y1
y2 (x)
(x)
梁的变形

梁的变形

1 2 1 3 C1 PL ; C 2 PL 2 6
2
写出挠曲线方程和转角方程，并画出挠曲线
P v( x ) ( L x )3 3 L2 x L3 6 EI P q ( x ) v' ( L x )2 L2 2 EI
最大挠度及最大转角


v
P L
度量梁变形的两个基本量
1.挠度：横截面形心沿垂直于轴线方向的线位移。用v 表示。
v向下为正，反之为负。
2.转角：横截面绕其中性轴转动的角度。用q 表示， 顺时针转动为正，反之为负。
C v v
q
P x
C’
转角与挠度的关系
挠曲线上任一点的纵坐标 v（x）即为该点的
横截面的挠度。
dv tgq v' dx
qmax
x


vmax
PL3 v ( L) ( ) 3 EI
q max
PL2 q ( L) ( ) 2 EI
例： 简支梁受集中力F作用，求梁的转角方程和挠度方程， 并求C截面的挠度和A截面的转角。已知梁的EI，l=a+b，a>b。 解：1）由梁整体平衡分析得： HA
H A 0, RA Fb Fa , RB l l
前面讨论了(梁）弯曲 内力、弯曲应力，接下
来讨论弯曲变形。
第10章
梁的变形
梁在外力作用下除了限制其应力，使其满 足强度条件外，还必须限制它的变形，即必须 具有足够的刚度，满足刚度条件。 例如：楼板弯曲变形太大.则平顶下面的粉 刷层就会剥落，不但影响美观，而且给人以不 安全的感觉；高速铁路桥梁变形过大，就无法 提高行车速度。
2、尽量减小梁的跨度或长度，减少弯矩数值

梁挠曲的近似微分方程完美版PPT


第二强度理论（最大伸长线应变理论）
– 这一理论认为，最大伸长线应变ε1达到单向 拉伸的极限值ε1jx ，材料就发生脆性断裂；
即： 或： σ1-ν（ σ2 + σ3 ）/E = σb/E；
σr1＝ σ1≤[σ]，
ε =ε ；或： σ -ν（ σ + σ ）/E = σ /E； 实验证明，该强度理论较好地解释了石料、混凝土等脆性材料受轴向拉伸时，沿横截面发生断裂的现象。
r 4 1 2 (1 2 ) 2 (2 3 ) 2 (3 1 ) 2
式中： σr4是按第四强度理论计算的相当应力。
– 实验证明，第四强度理论比第三强度理论更符合实验结果， 因此在工程中得到广泛的应用。
材料力学电子教程
第七章 应力状态
强度理论的适用范围
在三向拉伸应力状态，无论是脆性材料还是塑性材料，都 会发生断裂，应采用最大拉应力理论，即第一强度理 论。
在三向压缩应力状态，无论是脆性材料还是塑性材料，都 会屈服破坏裂，适于采用形状改变比能理论或最大切 应力理论，即第四或第三强度理论。
一般而言，对脆性材料宜采用第一、第二强度理论。
一般而言，对塑性材料宜采用第三、第四强度理论。
σr3 =σ1－ σ3≤[σ] 式中： σr3 称为按第三强度理论计算的相当应力
– 实验证明，这一理论可以较好的解释塑性材料出 现塑性变形的现象。但是，由于没有考虑σ2的影 响，故按这一理论设计构件偏于安全。
材料力学电子教程
第七章 应力状态
第四强度理论（形状改变比能理论）
– 这一理论认为，形状改变比能Ux是引起材料发生 屈服破坏的原因。也就是说，材料无论处在什么 应力状态下，只要形状改变比能Ux达到材料在单 向拉伸屈服时的形状改变比能Uxs，材料就发生屈 服破坏。即：(p291) Ux=Uxs 其强度条件为：

梁的位移分析与刚度设计


§8-2 梁的挠曲线近似微分方程及其积分
一、梁的挠曲线近似微分方程式
曲线 y f (x)的曲率为
y K
(1 y 2 ) 3/2
1M
EI z
1
v (1 v 2 ) 3/2
v
M v 或 EIv M EI z
y M0
M v 0 M
y M0
M v 0 M
x
x
EIv M
梁的挠曲线近似微分方程:
第八章 弯曲变形 静不定梁 §8-1 概 述
一、工程实践中的弯曲变形问题 在工程实践中，对某些受弯构件，除要求
具有足够的强度外，还要求变形不能过大，即 要求构件有足够的刚度，以保证结构或机器正 常工作。
摇臂钻床的摇臂或车床的主轴变形过大， 就会影响零件的加工精度，甚至会出现废品。
桥式起重机的横梁变形过大,则会使小车 行走困难，出现爬坡现象。
A
v Px (4x2 3l2 ) 48EI
x l
C
l
B
x
2
2
最大转角和最大挠度分别为：
max
A
B
Pl 2 16EI
v max
v
x l 2
Pl 3 48EI
例：已知梁的抗弯刚度为EI。试求图示简支 梁的转角方程、挠曲线方程，并确定θmax和vmax。
y
q
A
C
D
E
B
x
a
a
a
a
解：由对称性，只考虑半跨梁ACD
EIv M (x) 或:
d2v EI M (x)
dx 2
二、用积分法求梁的变形
EIv M(x)
EIv M(x) dx C
EIv M(x) dx dx Cx D

概述梁的挠曲线近似微分方程及其积分用积分


y
a
P
A x1
C
x2
L
x B
EIw
0
P(a
x1)
(0 x1 a) (a x2 L)
EIw
P 2
x12
Pax1
C1
C2
EIw
P
6
x13
Pa 2
x12
C1x1
D1
C2 x2 D2
确定积分常数 边界条件
EI 0 x1 0
EI w 0 x1 0
C1 0 D1 0
连续性条件
当 x1 x2 a 时，
讨论题：指出下列梁的边界条件。
q
q
A
A
B
a
l
a
B L
连续性条件: 挠曲线上任意点有唯一确定的挠度和转角。 若连续性条件不满足，则挠曲线就不连续(图a)和不光滑(图b)。
A
C
B
A
C
B
（图a）
（图b）
对上述梁：
边界条件： wA 0, wB 0
连续性条件： wC左 wC右 , C 左 C 右
挠曲线近似微分方程
(x2 )
dw(x2 ) dx2
Pa 2 2EI
y
a
P
C
Bx
C wB
L
例2 求图示梁自由端的转角和挠度。
P
EI
2EI
解： 建立坐标系并写出弯矩方程
A x1
B x2 C
a
a
AB段 (0 x1 a)
M 1 Px1
BC段 (0 x2 a)
M 2 P(a x2 )
写出挠曲线微分方程并积分
AB段 EIw1 M1 Px1
3 2EI

梁的变形,挠曲线微分方程及其积分


w
M (x)dx EI
C
w
M (x) EI
dxdx
Cx
D
3.积分常数C、D的确定
边界条件
θ
连续性条件 w1 w2
1 2
（c)
4.挠曲线的大致形状
正的弯矩，挠曲线向上凹 负的弯矩，挠曲线线上凸
积分法求梁的弯曲变形 ---例题
例 如图示的悬臂梁，抗弯刚度为EI，集中载荷F,求 w(x)、θ(x)及wmax、θmax。
将边界条件代入(1)(2)两式
22
挠曲线近似微分方程：
D=0 C ql3 24
EIw M (x) ql x 1 qx2 22
积分得
EIw ql x2 q x3 C — (1)
EIw EI
EIw
ql 12
x3
ql x2 q x3 46 q x4 ql3 24 24
x
ql 3 24
46
EIw ql x3 q x4 Cx D — (2) 12 24
边界条件为
x 0, wA 0 x l, wB 0
max
A
B
ql 3 24EI
wmax
w x l 2
5ql 4 384EI
例 如图示的简支梁，抗弯刚度为EI，集中载荷F,求 w(x)、θ(x)及wmax、θmax。
对各段梁，都是由坐标原点到所研究截面之间的 梁段上的外力来写弯矩方程的。所以后一段梁的 弯矩方程包含前一段梁的弯矩方程。只增加了 （x-a）的项。
对（x-a）的项作积分时，应该将（x-a）项作为 积分变量，从而简化了确定积分常数的工作。
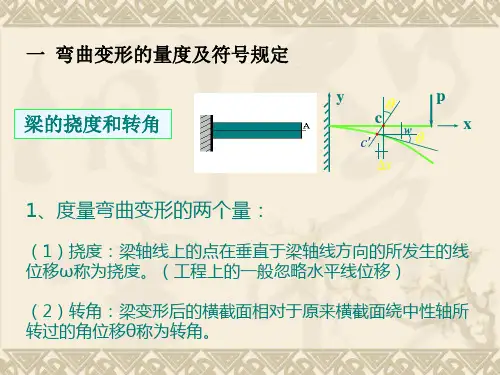
梁的变形，挠度和转角 挠曲线近似微分方程
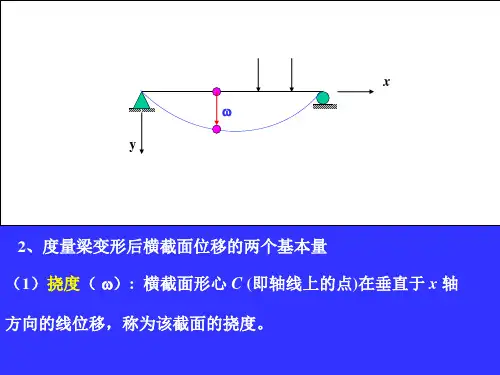
一、梁的弯曲变形 挠度w 挠曲线方程

挠曲线的近似微分方程


Bx FBy
解：弯矩方程 :
M x 1 qlx 1 qx2
22
挠曲线的近似微分方程:
w

1 EI z

1 2
qlx

1 2
qx2

进行一次积分得：
w

1 EI z

1 4
qlx2

1 6
qx3
C

再进行第二次积分得：
w

1 EI z
1 12
qlx3
Tmax 180 [] GIp
一般传动轴， [φ’] = 0.5 ~1/m
例4 图为一圆截面轴 AC ，受扭转力偶矩MA，MB 与Mc作用。 已知MA =90 N·m , MB =160 N·m ， MC =70 N·m ， l=2 m， G=80 GPa ， IP=3.0×105 mm4 ， [φ’] =0.3 (o)/m 。试计算 该轴的总扭转角 φAC （即截面C对截面A的相对转角），并 校核轴的刚度。
F C、D为积分常数，它由位移边界与连续条件确定。
边界条件：梁截面的已知位移条件 固定端的挠度和转角均为零，铰支座处的挠度为零。
A
wA=0 θA=0
F B
A wA=0
F C
B
wC1=wC2 wB=0 θC1=θC2
$ 挠曲轴在C点连续且光滑 连续条件：分段处挠曲轴应满足的连续、光滑条件
例6 如图所示图形为一外伸梁，承受集中载荷作用，试绘制
B
w xl
ql3 6EI z
ql 4
wB
w xl
8EI z
根据挠度和转角的符号规定，上述结果表明转角为顺时针，挠度方 向为向下。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4）由位移边界条件确定积分常数
x 0, x 0,
代入求解
A 0 yA 0
1 2 1 3 C Fl , D Fl 2 6 5）确定转角方程和挠度方程 1 1 2 2 EI F (l x) Fl 2 2 1 1 2 1 3 3 EIy F (l x) Fl x Fl 6 2 6 6）确定最大转角和最大挠度 Fl 2 Fl 3 x l , max B , ymax y B 2 EI 3 EI
x1 a, x 2 b c左 c右 yc左 yc右
确定积分常数举例：
边界条件：
x 0 : y A x l : yB
连续条件： x l / 2时 : 0 C 左 C右 0 y C左 y C右
x 0 : y A 0 qla x l : y B 2 EA
4 EI z
解： 1）外力分析：
M0 M0 RA (), R B ( ) L L
2）内力分析：(M方程) 3）挠曲线方程和转角方程：
d2 y M0 EIz 2 x L dx
M0 M(x) x 0 x L L
M0 2 EIz θ x C 2L M0 3 EIz y x Cx D 6L
yC 1
3）将结果叠加
yB 2
yC 2
yC
y
i 1
2 i 1
2
Ci
41ql 4 384 EI
7 ql 3 48 EI
C

Ci
讨
论
叠加法求变形有什么优缺点？
9.8 梁的刚度条件及提高梁刚度的措施
1.刚度条件
y max [ y ],

max
[ ]
例、 已知EIZ，M0，L，求θ A，θ B，及中点的挠 ML2 度； 若 y ，试校核刚度。
[ y]
刚度满足要求。
2.提高梁刚度的措施：
1）选择合理的截面形状增大截面惯性矩
2）改善结构形式，减小弯矩数值
3）采用超静定结构
小
结
基本要求： 掌握弯曲的概念和实例，梁的计算简图，掌握纯弯曲的正应力 公式，弯矩与挠曲线曲率间的关系，抗弯刚度，抗弯截面模量， 纯弯曲理论的推广，熟练掌握梁按正应力的强度计算。 掌握矩形截面梁的剪应力，工字形截面梁的剪应力，梁按剪应 力的强度校核，提高弯曲强度的措施。 掌握梁的变形和位移，挠度和转角，梁的挠曲线及其近似微分 方程，用积分法求梁的挠度转角，根据叠加法求梁的挠度转角， 梁的刚度校核，提高梁的刚度措施。 重点： 梁按正应力的强度计算，梁按剪应力的强度校核。 难点： 梁的刚度校核。
dy tan dx
y (x)
表明：挠曲线上某点切线的斜率等于该点横截面的转角。
2.挠曲线的近似微分方程：

推导弯曲正应力时，得到：
1 M ρ EI z
忽略剪力对变形的影响
1 M ( x) ( x) EI z
由数学知识可知：
d2y 1 dx 2 dy 2 3 [1 ( ) ] dx
例1 求梁的转角方程和挠度方程，并求最大 转角和最大挠度，梁的EI已知。
解: 1）由梁的整体平衡分析可得：
2）写出x截面的弯矩方程
A
)
F B
X A 0, YA F (), m A Fl (
x
l
yB
B
x
M ( x ) F (l x ) F ( x l )
y
3）列挠曲线近似微分方程并积分 d2y EI 2 M ( x) F (l x) dx dy 1 积分一次 EI EI F (l x) 2 C dx 2 1 再积分一次 EIy F (l x) 3 Cx D 6
为了利用梁全长承受均 布载荷的已知结果，先将均 布载荷延长至梁的全长，为 了不改变原来载荷作用的效 果，在AB 段还需再加上集 度相同、方向相反的均布载 荷。
yC
2）再将处理后的梁分解为简单 载荷作用的情形，计算各自C截 面的挠度和转角。
ql 4 ql 3 y C1 , C1 8EI 6 EI l yC 2 y B 2 B 2 2 ql 4 ql 3 l , 128EI 48 EI 2 ql 3 C2 48EI
2
9.6 积分法求弯曲变形
挠曲线的近似微分方程为：
d y M ( x) EI z dx 2
2
d2y EI z 2 M ( x) dx
积分一次得转角方程为：
dy EI z EI z M ( x)dx C dx
再积分一次得挠度方程为：
EI z y M ( x)dxdx C x D
4）确定积分常数：
x 0, y0 yA 0
x L, yL yB 0
得：
D0
M0 2 M0L 所以 EIz θ x 2L 6 M0 3 M0L EIz y x x 6L 6
M0L C 6
5）求θ A，θ B。
M0L （ A 0 6 EI Z M0L B L （ 3EI Z
9.5 梁的位移与挠曲线近似微分方程
1.基本概念:
转角
挠度 挠曲线 1、弯曲变形的表示方法：
y
（1）挠度y：截面形心在y 方向的位移;
x
y
x
挠曲线方程：
y y( x )
（2）转角θ:某横截面绕 自己的中性轴转动的角度。 转角方程：
由于小变形，截面形心在x方向的 位移忽略不计挠度转角关系为：
）
）
中点的挠度： M0 1 3 M0L 1 L EIz y ( ) ( L) ( L) 2 6 2 6 2
M 0 L2 L y( ) () 2 16 EIz
6）刚度校核：
y' 0(即θ 0处) L x 3
M0 2 M0L x 0 2L 6
y max
M0L
2
9 3EI Z
讨
论
积分法求变形有什么优缺点？
9.7 叠加法求梁的变形
梁在若干个载荷共同作用时的挠度或转角，等 于在各个载荷单独作用时的挠度或转角的代数和。 这就是计算弯曲变形的叠加法。 即叠加法是： 分别求出各载荷单独作用时的变形，然后把各载荷在 同一处引起的变形进行叠加(代数叠加)。
直接查表： pl 3 Pl 2 y BP BP 3EI 2 EI ql 4 ql 3 y Bq Bq 8 EI 6 EI 由叠加法得：
略去高阶小量，得
d2y 2 dx 1
所以
d 2 y M ( x) 2 dx EI z
由弯矩的正负号规定可得，当y坐标向下时，弯 矩的符号与挠曲线的二阶导数异号，所以挠曲线的 近似微分方程为：d y M ( x) 2 EI Nhomakorabeaz dx
EIZ——抗弯刚度 由上式进行积分，就可以求出梁横截面的转角 和挠度。
积分常数利用梁的边界条件及连续光滑条件来求得。
边界条件：梁横截面的已知位移条件或约束条件。
连续光滑条件：在相邻梁段的交接处即分段处， 相连两截面应具有相同的转角与挠度。
确定积分常数举例：

边界条件：
连续条件：
x0: A 0 x0: y A 0
x1 0, y A 0 x2 0, yB 0
y B y BP Pl 3 ql 4 y Bq 3EI 8EI
B BP Bq
pl 2 ql 3 2 EI 6 EI
yC
例 已知：悬臂梁受力如 图示，q、l、EI均为已知。 求C截面的挠度yC和转角C
解: 1）首先，将梁上的载荷变成 有表可查的情形