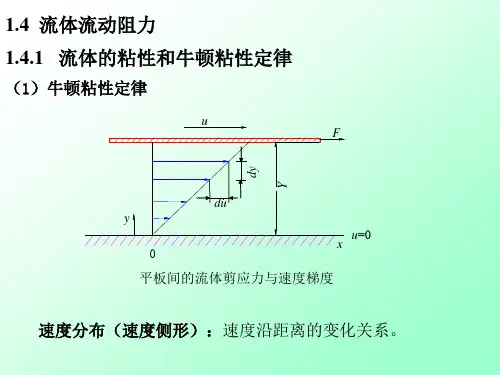
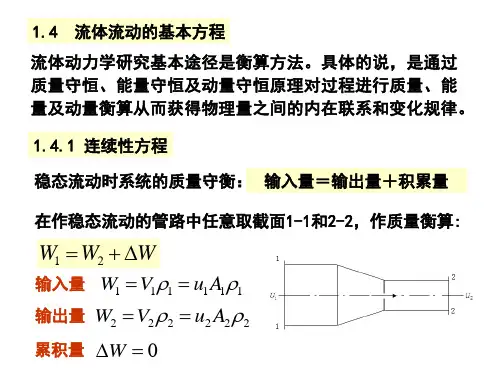
u2 2
ζ ----局部阻力系数(local resistance factor) 由实验测得。
若用压强降来表示 ,则:
= △ P = ρ hf ′
ρ u2 ζ2
1.5 流体在管内的流动阻力∑hf
局部阻力系数---- ζ • 管路突然放大或突然缩小, ζ值由小管与大管的截
面积之比A1/A2查得,且流速取小管的流速。
阻力通式:
∑ h f = hf+hf ′ =λ
l + le u2 d2
∑hf
=
hf+
hf ′ =
(λ
l d
+ζ )
u2 2
1.5 流体在管内的流动阻力∑hf
例 : 用泵把20℃苯从地下贮罐送到高位槽, 流量300L/min, 高位槽液面比贮罐液面高10m, 上方均为大气压. 泵的吸入 管为φ89mm×4mm 的无缝钢管, 长15m, 管路上装有一全 开的底阀, 一个标准弯头, 泵排出管为φ57mm×3.5mm无缝 钢管, 长50m, 一个全开的闸阀, 一个全开的截止阀和3个标 准弯头, 假设贮罐送和高位槽的液面维持恒定, 求泵的轴功 率, 设泵的效率为70%.
层流边界层厚度:
δ x=
4.64 Rex0.5
湍流边界层厚度: δ 0.376
x = Rex0.2
Rex = us x ρ μ
当Rex 2105时,边界层内的流动为滞流 ;
当Rex 3106时, 边界层内的流动为湍流;
在平板前缘处,x=0,则δ=0。随着流动路程的增长,边界层 逐渐增厚;随着流体的粘度减小,边界层逐渐减薄。
1.4 流体流动现象
速度和压力围绕“平均值”——时均速度波动,该值 不随时间改变