当前位置：文档之家 › 偶函数课件.ppt

偶函数课件.ppt

  • 格式：ppt
  • 大小：1.39 MB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

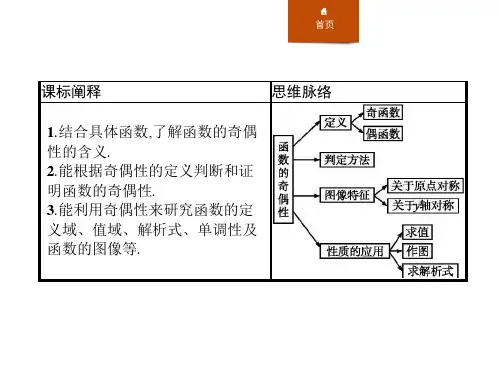
函数的奇偶性函数教学课件

函数的奇偶性函数教学课件

探究一探究二探究三思维辨析当堂检测反思感悟由函数奇偶性求函数
探究一
探究二
探究三
思维辨析
当堂检测
若本例题中题干不变,如何求当x≤0时,f(x)的表达式?解:只需将f(0)单独求出.因为f(x)是奇函数,且在x=0处有定义,所以f(0)=0.又因为f(x)=x|x+2|,x<0,所以f(x)=x|x+2|,x≤0.
探究一探究二探究三思维辨析当堂检测利用函数的单调性与奇偶性解
探究一
探究二
探究三
思维辨析
当堂检测
1.(多选)下列函数是偶函数的为( )A.f(x)=x2 B.f(x)=xC.f(x)= D.f(x)=x2+x4答案:AD
探究一探究二探究三思维辨析当堂检测1.(多选)下列函数是偶函
探究一
探究二
探究三
思维辨析
当堂检测
2.有下列说法:①偶函数的图像一定与y轴相交;②若y=f(x)是奇函数,则由f(-x)=-f(x)可知f(0)=0;③既是奇函数也是偶函数的函数一定是f(x)=0,x∈R;④若一个图形关于y轴成轴对称,则该图形一定是偶函数的图像.其中不正确的是( )A.①② B.①④ C.①②④ D.①②③④解析:①中可举反例f(x)=x2+2,x∈(-∞,-2)∪(2,+∞);②中f(x)在x=0处可能无定义;③中也可以是f(x)=0,x∈A(A为关于原点对称的数集);④中该图形可能不是函数的图像.故①②③④均错误.答案:D
一二解析:①中函数的定义域不关于原点对称,所以①表示的不是偶
探究一
探究二
探究三
思维辨析
当堂检测
判断函数的奇偶性例1判断下列函数的奇偶性:
分析:先求定义域,验证定义域是否关于原点对称,再看f(-x)与f(x)的关系,进而做出判断.
函数的奇偶性PPT精品课件

函数的奇偶性PPT精品课件

∴f(x)为非奇非偶函数
思考3：
在前面的几个函数中有的是奇函数，有的是偶函数，也有非奇非偶函数。那么有没有这样的函数，它既是奇函数又是偶函数呢？
有。例如：函数 f(x)=0
是不是只有这一个呢？若不是，请举例说明。
x
y
0
1
f(x)=0
-1
奇函数 偶函数 既奇又偶函数 非奇非偶函数
01
根据奇偶性, 函数可划分为四类:
例1. 判断下列函数的奇偶性
(1) f(x)=x3+x (2) f(x)=3x4+6x2 +a
解: 定义域为R ∵f(-x)=(-x)3+(-x) = -x3-x = -(x3+x) 即 f(-x)= - f(x) ∴f(x)为奇函数
函数的奇偶性
点此播放讲课视频
在日常生活中，有非常多的轴对称现象，如人与镜中的影关于镜面对称，请同学们举几个例子。
03
而我们所学习的函数图像也有类似的 对称现象，请看下面的函数图像。
除了轴对称外，有些是关于某点对称，如风扇的叶子，如图： 它关于什么对称？
04
点此播放讲课视频
观察下面两组图像，它们是否也有对称性呢？
x
y
O
1
-1
f(x)=x2（1）Fra bibliotek（2）y
x
O
x0
-x0
例如：对于函数f(x)=x3
有 f(-1)=(-1)3=-1 f(1)=1
f(-2)=(-2)3=-8 f (2)=8
f(-x)=(-x)3=-x3
f(-1)= - f(1) f(-2)= - f(2) f(-x)= - f(x)
-x
结论:当自变量x任取定义域 中的一对相反数时,对应的 函数值相等，即f(-x)=f(x)
偶函数的定义与性质PPT课件

偶函数的定义与性质PPT课件


x
P' (2,4) 2
P'( x , x2)
4
P2 (2,4)
x2
P(x , x2)
f (x) x
f x x2
特征 1.定义域关于原点对称；
： 2. f x f x
一、偶函数
1、偶函数的定义：
一般地，如果对于函数f(x)的定
任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶
函数（even function）。
注意：定义域关于原点对称
2、偶函数的性质 A、偶函数图象关于y轴对称，反之亦然； B、偶函数在关于原点对称的两个区间上，单调性相反。
二、例题剖析
例1. 判断函数下列函数是否为偶函数？
(1) f x 2x2 1; x [2,2); (2) f x x3 x2.
解：(1)由于f x 2x2 1的定义域为 2,2
§1.3.2 偶函数的定义与性质
• 观察下列函数的图象，从图象对称的角度把这些函数图象分 类：
y f (x) x2
y f (x) | x |
y f (x) 1
| x|
x O
(1) y f (x) x x
(4)
x O
(2)
y f (x) x3 x
O (5)
x O
(3)
y f x x 1
x O
P1 (1,1)
1
x
P' (2,4) 2
P'( x , x2)
4
P2 (2,4)
x2
P(x , x2)
y
P'(x, x )
P' 2
2,2
P' 1
1,1
x
函数的奇偶性对称性周期性课件共19张PPT

函数的奇偶性对称性周期性课件共19张PPT


(2)已知 f (x) 是奇函数，且当 x 0 时，f (x) eax .若 f (ln 2) 8 ，则a ___-_3______.
(3)(2020·海南 8)若定义在 R 的奇函数 f(x)在(, 0) 单调递减，且 f(2)=0，则满足
xf (x 1) 0 的 x 的取值范围是（ D ）
A．13
B． 2
C．
13 2
D．123
专题三：函数的周期性
变式 5：(1)设定义在 R 上的函数 f x 满足 f x 2 f x ，若 f 1 2 ，则 f 99 _-_2__.
(2)(2022·湖北模拟)定义在 R 上的函数 f x 满足 f x 1 f x 2 ，则下列是周期函数的是 （ D ）A． y f x x B． y f x x C． y f x 2x D． y f x 2x
叫做偶函数 一般地，设函数f(x)的定义域为I，如果∀x∈I， 奇函数 都有－x∈I，且_f_(－__x_)_＝__－__f_(x_)_，那么函数f(x) 关于_原__点__对称 就叫做奇函数
复习回顾 2.周期性 (1)周期函数：一般地，设函数f(x)的定义域为D，如果存在一个非零常数 T，使得对每一个x∈D都有x＋T∈D，且_f_(_x＋__T__)＝__f_(x_)_，那么函数y＝f(x) 就叫做周期函数，非零常数T叫做这个函数的周期. (2)最小正周期：如果在周期函数f(x)的所有周期中存在一个最_小___的正数， 那么这个_最__小__正__数__就叫做f(x)的最小正周期.
课堂小结
函数的性质
奇偶性
判断 求解析 求参数
对称性
轴对称： 中心对称：
周期性
求值 求解析 比较大小
祝同学们前程似锦！
函数的奇偶性ppt课件

函数的奇偶性ppt课件


例4.1若函数f x ax21 bx 3x b是偶函数，定义域
a 1，2a，则实数a _3__，b _-_3_.
2已知函数f x x 1x a为奇函数，则实数a _-_1_.
x
例5.已知函数y=f(x) 在R上是奇函数,而且在 (0,+∞)上是增函数,判断y=f(x)在(-∞,0)的单调 性，并证明你的判断.
观察函数f(x)=x和f(x)=1/x的图像回答问题
（1）这两个函数图象有什么共同特征？ （2）填函数值对应表
x f(x)=x
-3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3
x
-3 -2 -1 1 2 3
f(x)=
1 x
13
1 2
-1
1
11 23
2.奇函数的概念
如果对于函数f(x)的定义域内任意一个x, 都有f(-x)=-f(x),那么函数f(x)就叫做奇函数.
练习：已知函数y=f(x)是偶函数，它在y 轴右边的图象如图，画出y=f(x)在 y轴左 边的图象.
解:
y
O
x
变式：若f(x)是奇函数呢？
例2. 判断下列函数的奇偶性
(1) y x2(2 x 3);
2 f x x3 2x
3 f x 2x4 3x2
4 f x x 2
(5)
f
x
x x
1, 1,
x x
0 0
注：奇、偶函数的定义域一定关于原点对称，
若函数的定义域不关于原点对称，则不具有奇偶性。
判断函数奇偶性的两种方法： (1)定义法:
(2)图象法:
利用函数的奇偶性求解析式
课堂篇 究学习
例3. 已知f(x)为R上的奇函数,当x>0时,f(x)=-2x2+3x+1,
人教版函数的奇偶性-高中数学(共41张PPT)教育课件

人教版函数的奇偶性-高中数学(共41张PPT)教育课件


f(－x)＝ f(x) 函数f(x)叫作偶函数
图象关于 y轴 对称
f(－x)＝ －f(x) 函数f(x)叫作奇函数 图象关于 原点 对 称
3
知识点聚焦：
• 二、奇偶性
定义
如果函数f(x)是奇函数或是偶函数，那么就说函数 f(x)具有 奇偶性
图象特征 奇(偶)函数 图象关于原点或y轴对称
4
探究一 函数奇偶性的判断
∵f(x)是奇函数，
•
∴f(x)＝－f(－x)＝－[(－x)(1＋x)]＝x(1＋x)．
• 【答案】B
37
随堂训练
• 5．已知函数f(x)是定义域为R的奇函数且f(1)＝－2，那么f(－1)＋f(0)＝( )
•
A．－2
B．0
C．1
D．2
38
解析：
• 【解析】函数f(x)是定义域为R的奇函数且f(1)＝－2，
•
: 其实兴趣真的那么重要吗？很多事情我 们提不 起兴趣 可能就 是运维 我们没 有做好 。想想 看，如 果一件 事情你 能做好 ，至少 做到比 大多数 人好， 你可能 没有办 法岁那 件事情 没有兴 趣。再 想想看 ，一个 刚来到 人世的 小孩， 白纸一 张，开 始什么 都不会 ，当然 对事情 开始的 时候也 没有 兴趣这 一说了 ，随着 年龄的 增长， 慢慢的 开始做 一些事 情，也 逐渐开 始对一 些事情 有兴趣 。通过 观察小 孩的兴 趣，我 们可以 发现一 个规律 ，往往 不是有 了兴趣 才能做 好，而 是做好 了才有 了兴趣 。人们 总是搞 错顺序 ，并对 错误豪 布知晓 。尽管 并不绝 对是这 样，但 大多数 事情都 需要熟 能生巧 。做得 多了， 自然就 擅长了 ；擅长 了，就 自然比 别人做 得好； 做得比 别人好 ，兴趣 就大起 来，而 后就更 喜欢做 ，更擅 长，更 。。更 良性循 环。教 育小孩 也是如 此，并 不是说 买来一 架钢琴 ，或者 买本书 给孩子 就可以 。事实 上，要 花更多 的时间 根据孩 子的情 况，选 出孩子 最可能 比别人 做得好 的事情 ，然后 挤破脑 袋想出 来怎样 能让孩 子学会 并做到 很好， 比一般 人更好 ，做到 比谁都 好，然 后兴趣 就自然 出现了 。
3.2.1 函数的奇偶性 课件(共26张PPT)(2024年)

3.2.1 函数的奇偶性 课件(共26张PPT)(2024年)


f(x)
g(x) f(x)+g(x) f(x)-g(x)
偶函数 偶函数 偶函数
f(x)g(x
)
f[g(x)]
注
意:f[g(x)]
偶函数 偶函数 偶函数 中,g(x)的
偶函数 奇函数 不能确定 不能确定 奇函数 偶函数 值域是f(x)
奇函数 偶函数 不能确定 不能确定 奇函数 偶函数 的定义域
奇函数 奇函数 奇函数
活动二：新知探究
偶函数的定义：
一般地，设函数 f（x）的定义域为 I ，如果∀x∈I,都
有-x∈I,且f(-x)=f(x), 那么函数 f（x）就叫做偶函数.
活动二：新知探究
偶函数的几点说明：
（1）偶函数的定义域必关于原点对称，即若 x 是定义域内的
一个值，则 –x 也一定在定义域内.
（2）“函数 f（x）为偶函数”是“函数 f（x）图象关于y轴对
奇函数 偶函数 奇函数 的子集.
活动二：新知探究
类比函数单调性，你能用符号语言精确地描述“函数图象
关于y轴对称”这一特征吗？
不妨取自变量的一些特殊值，观察相应函数值的情况
x
···
-3
-2
-1
0
1
2
3
···
f(x)=x²
···
9
4
1
0
1
4
9
···
g(x)=2-|x|
···
-1
0
1
2
1
0
-1
···
可以发现，当自变量取一对相反数时，相应的两个函数值相等.
称”的充要条件.
活动二：新知探究
1

探究：观察函数 f(x)=x和g(x)= 的图象，你能发现这两个函数
函数的奇偶性和单调性1-课件

函数的奇偶性和单调性1-课件

$f(x) = x^3$，满足$f(-x) = f(x)$，在全域上单调递增。
偶函数实例
$f(x) = x^2$，满足$f(-x) = f(x)$，在$x geq 0$时单调递增 。
单调性实例分析
单调递增函数实例
$f(x) = x$，在全域上单调递增。
单调递减函数实例
$f(x) = frac{1}{x}$，在$( - infty ,0)$和$(0, + infty)$上单调递减。
非奇非偶函数
定义
既不是奇函数也不是偶函数的函 数称为非奇非偶函数。
特性
非奇非偶函数的图像既不关于原点 对称也不关于y轴对称。
举例
$f(x)=x+1$是非奇非偶函数，因为 $f(-x)=-x+1neq -f(x)$且$f(-x)neq f(x)$。
02
CHAPTER
函数的单调性
单调增函数
定义
对于函数$f(x)$的定义域内的任意 $x_1$和$x_2$（$x_1 < x_2$），如 果$f(x_1) < f(x_2)$，则称函数$f(x)$ 在其定义域内单调递增。
奇偶性与单调性的综合应用
利用奇偶性和单调性判断函数的值域
根据函数的奇偶性和单调性，可以判断函数在不同区间的值域，进而确定整个函 数的值域。
利用奇偶性和单调性判断函数的极值
根据函数的奇偶性和单调性，可以判断函数在不同区间的增减性，进而确定函数 的极值点。
04
CHAPTER
实例分析
奇偶性实例分析
奇函数实例
递减。
性质
单调减函数的图像是沿x轴方向 下降的。
举例
正比例函数$y = -kx$（$k > 0$ ）和指数函数$y =
函数的奇偶性ppt课件

函数的奇偶性ppt课件

2.4.1函数的奇偶性
北师大版（2019）必修第一册
学习目录
PARENT CONFERENCE DIRECTORY
壹
学习目标
叁
题型突破
Learning Objectives
Breakthrough in question types
贰
探索新知
肆
当堂检测
Explore new knowledge
Classroom test
PART 01
学 习 目 标
01
学习目标
01
结合具体函数，了解奇偶性的概念和几何意义
02
掌握函数奇偶性的判断和证明方法
03
会用奇、偶函数图象的对称性解决简单问题
PART 02
探 索 新 知
02
探索新知
情境导学
（1）这些图形是什么对称图形？
（2）对称轴分别在哪里？
02
探索新知
情境导学
（1）这些图形是什么对称图形？
关于原点对称，那么它是奇函数，如果一个函数的图象关于y轴对称，那么它是偶函数.
2.若奇函数在x＝0处有定义，则其图象一定过原点.
3.对于偶函数f(x)，我们有f(x)＝f(|x|)
02
探索新知
例2 根据定义，判断下列函数的奇偶性：
（1）f（x）＝ －2x5 ；
1
（3）h（x）＝ 2 ；

（2）g（x）＝x4＋2；
证明：根据函数关于点A(a，b)中心对称的定义，p(x，y)的对称点p′(x′，y′)有如
下等式
+′
2
= ，
+′
2
= .我们得到：x′＝2a－x，y′＝2b－y
函数的奇偶性课件(共14张PPT)

函数的奇偶性课件(共14张PPT)


y
则f (x) f (x) 2x
即2 f (x) 2x
2
即f (x) x
-2 o
2
x
故解集为：- 2，-1 0,1
-2
高中数学必修1同步辅导课程——函数的奇偶性
变式2：定义在R 上的函数 f (x), 对任意x, y R都有 f (x y) f (x) f ( y) 1, 且x 0时，f (x) 1, f (1) 2
f (x)单调递减，则f (1 m) f (m) 成立的 m 取值范围 是 ________。
高中数学必修1同步辅导课程——函数的奇偶性
例2：定义在 3,3 上的函数 f (x), g(x)分别为偶函数、
奇函数，图像如下，则不等式 f (x) 0的解集是：
g(x)
(_2_,_1_)__(_0_,1_) __(_2,_3_) 。
(1)求证：f (x)是R上的增函数； (2)解不等式： f (3x 1) 7; (3)求证：g(x) f (x) 1是奇函数。
高中数学必修1同步辅导课程——函数的奇偶性
课堂总结：
1：函数奇偶性的定义： “数”与“形”的特征
2：利用函数的奇偶性求值、求解析式
3：函数奇偶性与单调性的联系： “模拟图像”
题型三：奇偶性与单调性的联系：
例：已知函数 y f (x)(x 0)为奇函数，在 x 0,
上为单调增函数，且 f (1) 0 ，则不等式 f (2x 1) 0 解集为__________.
高中数学必修1同步辅导课程——函数的奇偶性
变式：定义在 2,2上的偶函数 f (x)，当x 0 时，
高中数学必修1同步辅导课程——函数的奇偶性
《奇函数偶函数》课件

《奇函数偶函数》课件

偶函数在其定义域内可导 或不可导，但偶函数在y轴 两侧的导数符号相反。
奇函数和偶函数的性质
01
奇偶性是函数的固有属 性，不随函数图像的平 移、伸缩或翻转而改变 。
02
奇函数和偶函数的定义 域必须关于原点对称。
03
奇函数和偶函数的定义 域可以是全体实数、正 实数、非负实数等。
04
奇函数APTER 02
奇函数和偶函数的图像
奇函数的图像
奇函数的图像关于原点对称，即对于 任意点$P(x, y)$在奇函数上，关于原 点对称的点$P'(-x, -y)$也在该奇函数 上。
奇函数的图像在坐标轴上的交点数量 是偶数。
奇函数的图像可能出现在第一、三、 五或七象限，但不可能出现在第二、 四象限。
奇函数的图像
奇函数的图像关于原点对 称。
奇函数的性质
奇函数在其定义域内可导 或不可导，但奇函数在原 点的导数一定为0。
偶函数的定义
偶函数的定义
如果对于函数$f(x)$的定 义域内任意一个$x$，都 有$f(-x)=f(x)$，则称 $f(x)$为偶函数。
偶函数的图像
偶函数的图像关于y轴对称 。
偶函数的性质
数的性质和应用
06
思考题
总结词：拓展思维
总结词：培养创新能力
总结词：思考奇偶函数在 实际生活中的应用
总结词：激发探索精神
总结词：探究奇偶函数与 其他数学知识的联系
总结词：尝试设计一些有 趣的奇偶函数问题
THANKS FOR WATCHING
感谢您的观看
偶函数的图像
偶函数的图像关于y轴对称，即 对于任意点$P(x, y)$在偶函数上 ，关于y轴对称的点$P'( - x, y)$

北师大版高中数学必修1第二章4.1函数的奇偶性课件PPT

3
∵函数 = − 定义域为 = ≠ 0 ，

且对任意 ∈ ，
3
3
3
3
有 − = −
= ， − = − − = .
−

∴ − = − ，所以函数为奇函数.


2
+ 1.
导入课题 新知探究 典例剖析 课堂小结
练习1：画出下列函数的图象，并判断其奇偶性：
3
1
(1) = − ;
则有 = .
导入课题 新知探究 典例剖析 课堂小结
二、偶函数的概念
偶函数的概念：
设函数 = 的定义域，如果对任意的 ∈ ，有− ∈ ，
且 − = ()，那么就称函数 = 为偶函数.偶函数的图象
关于轴对称，反之亦然.
例如：证明函数 = 2 为奇函数.
−, > 等.
例如：函数 = 3 −1 < < 2 不是奇函数.
函数 = 2 −1 < ≤ 1 不是偶函数.
函数 = 0既是奇函数又是是奇函数.
函数 = 1是偶函数.
函数 = 3 0 ≤ ≤ 0 既是奇函数又是是奇函数.
注意：在研究函数时，如果知道它是奇函数或偶函数，就可以先研
∴ − ≠ − ， − ≠ ，
所以函数既不是奇函数也不是偶函数.
2
+ 1.
导入课题 新知探究 典例剖析 课堂小结
思考交流：利用定义判断函数的奇偶性
思考1：根据定义，判断下列函数的奇偶性：
2 +1+−1
2 + , ≤ 0
(1) = ቊ 2
(2) = 2
有 − = −2 −

函数的奇偶性的性质PPT教学课件


CH2—OH＋ 3HO C R 催化剂 CH —O—C—R ＋ 3H2O
加热
O
CH2—OH
CH2—O—C—R
2020/10/4
动物脂肪与植物油
2020/10/4
不同的油脂性质不同（R不同）
多数动物脂肪因饱和脂肪酸 甘油酯含量高在常温下呈固态
植物油因不饱和脂肪酸甘油 酯含量高而在常温下呈液态
油脂的生理功能
2020/10/4
水解 胃蛋白酶
氨基酸
酶
多肽
肽键 人体蛋白质
3、氨基酸
（1）结构：
羧酸分子中烃基上的氢原子被氨基 （ NH2）取代的产物。
（2）通式：
2020/10/4
O R CH—C—OH
NH2
（3）常见氨基酸及其酸碱性
甘氨酸 （H2N—CH2—COOH） (中性)
谷氨酸（HOOC—CH2—CH—COOH）
吃哪类油脂更利于健康
富含不饱和高级脂肪酸的植物油 特别是：必需脂肪酸的植物油
必需脂肪酸（P27）： 亚油酸 亚麻酸
花生四烯酸
2020/10/4
三、人必须吃含蛋白质的食物吗
1、蛋白质是构成人体的基础物质
人体内，肌肉、血液、内脏、神经、 毛发以及各种酶、抗体等都含有蛋白质。
2、蛋白质在人体内的转化
含有蛋白 质的食物
当x 0 时，f (x) x2 3x ,求 当x 0 时 f (x) 的解析式.
f (x) x2 3x(x 0)
例3、 设函数 f (x) 2x2 mx 3 ，
已知 f ( x 1) 是偶函数，求实数m的值.
例4、 已知f(x)是定义在R上的奇函数， 且对任意实数x都有 f (x 3) f ( x) 0 ，

函数的奇偶性(数学教学课件)课件

例如
$f(x)=x^3$，满足$f(-x)=-x^3=f(x)$，是奇函数。
偶函数实例
偶函数
如果对于函数$f(x)$的定义域内任意 一个$x$，都有$f(-x)=f(x)$，则称 $f(x)$为偶函数。
例如
$f(x)=x^2$，满足$f(-x)=(x)^2=x^2=f(x)$，是偶函数。
THANKS
函数的奇偶性
目录
• 奇偶性定义 • 奇偶性判断 • 奇偶性性质 • 奇偶性应用 • 奇偶性实例
01
奇偶性定义
Chapter
奇函数
定义
如果对于函数$f(x)$的定义域内任意一个$x$，都有 $f(-x)=-f(x)$，则称$f(x)$为奇函数。
性质
奇函数的图像关于原点对称。
实例
$f(x)=x^3$，$f(-x)=-(-x)^3=-x^3=-f(x)$，满足奇 函数的定义。
偶函数
定义
如果对于函数$f(x)$的定义 域内任意一个$x$，都有$f(x)=f(x)$，则称$f(x)$为偶函 数。
性质
偶函数的图像关于y轴对称。
实例
$f(x)=x^2$，$f(-x)=(x)^2=x^2=f(x)$，满足偶函 数的定义。
02
奇偶性判断
Chapter
奇函数判断
1 2 3
奇函数定义
如果对于函数$f(x)$的定义域内任意一个$x$， 都有$f(-x)=-f(x)$，则称$f(x)$为奇函数。
奇函数性质
奇函数的图像关于原点对称，即如果$f(x)$是奇 函数，那么其图像在$x$轴上方的部分与下方的 部分关于原点对称。
奇函数举例
例如，函数$f(x)=x^3$和$f(x)=sin(x)$都是奇函 数。

函数的的奇偶性PPT教学课件


又∵f(x)在(-1,1)上为减函数， ∴
1-a>a2-1 -1<1-a<1 -1<a2-1<1,解得0<a<1.
（2）因为函数g(x)在［-2,2］上是偶函数，则由g(1-m)<g(m)，可得g(|1m|)<g(|m|),
又当x≥0时，g(x)为减函数，得到
|1-m|≤2 |m|≤2
1 解之得-1≤m< 2
（4）f(x)= 1 x2 x2 1
.
x
11
(1)x x 定1 1
(x)2 1 x2 x2
义 域 为
x1 x
得x2 1
（
3 ）
函
数
的
定
义
域
为
A
=
{
学点二 由奇偶性求函数解析式 设f(x)是定义在R上的奇函数，当x>0时，f(x)= x2 +x+1,求 函数解析式. 【分析】由奇函数的图象关于原点对称，找x≥0和x<0时解析 式间的联系.
（2）如果一个函数的定义域关于原点不对称，那么这个 函数既不是奇函数，也不是偶函数.
（3）定义域关于原点对称，满足f(-x)=-f(x)=f(x)的函数， 既是奇函数，又是偶函数，如f(x)=0,x∈R.
判断下列函数的奇偶性：
1
1
（1）f(x)=x+ （3）f(x)=x+
xx
;
1
;
（2）f(x)=x2+ x2 ;
|1-m|>|m|,.
1.在函数的奇偶性中应注意什么问题？
（1）对于函数奇偶性的理解
①函数的奇偶性与单调性的差异:函数的奇偶性是相对于函数 的整个定义域来说的，这一点与函数的单调性不同.从这个意 义上来讲，函数的单调性是函数的“局部”性质，而奇偶性是 函数的“整体”性质，只有对函数定义域内的每一个值x，都 有f(-x)=-f(x)（或f(-x)=f(x)）,才能说f(x)是奇（或偶）函数.

高一数学人教版必修一函数的奇偶性 PPT课件 图文


猜想： f(x)f(x)
x ..3.2 1 0 1 2 3..
... f (x) x2
941
0
14
9..
偶函数的定义
一般地，如果对函数 f (x) 的定义域内任意一个 x, 都有f (x) f (x)， 那么函数 f (x)就叫偶函数 .
类比&探究
f(1)f(1) f(2)f(2) f(3)f(3)
1.3.2函数的奇偶性
必修1（人教版）
故宫
女子跳水10米跳台决赛，正反跳映衬对称美
数学&生活
生活中的对称美引入我们的数学领 域中，它又是怎样的情况呢？
请同学们观察下列函数图形，说出 他们各有怎样的对称性？
问题与思考
以上函数图像有什么共同特征呢？ 哈哈，我来回答
以上函数图像都关于y轴对称
把图像关于y轴对称函数称为偶函数
问题与思考
以上函数图像有什么共同特征 呢？
以上函数图像都关于原点对称
把图像关于原点对称函数称为奇函数
根据下列函数图象,判断其奇偶性.
y
y
o
奇函数
x
o
x 偶函数
y
b
oLeabharlann x 偶函数yo
x 奇函数
观察 & 发现
f(1)1f(1)
f(2)4f(2)
f( 3)9f(3) ……
2.两个性质:
一个函数为奇函数 它的图象关于原点对称。 一个函数为偶函数 它的图象关于y 轴对称。
3. 判断函数奇偶性的方法和步骤
我来总结
判断函数的奇偶性，注意定 义域优先
1.
课堂小结
f ( x )是 函数f (x)的图像 对函数 f (x)的定义
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、图像法： 对于用图像法表示的函数，观察图像 是否关于y轴对称。
数形结合很重要哦！
解决问题 深化定义
练习：判断下列函数是否为偶函数？
1、f（x）=
1 x2
2、书本56面练习2（3） 2,2
定义域关于原点 对称是判断偶函
数的必要条件
f (x) f (x) 要记好哦！
拓 展 问 题 注重应用
P2 (-3,2)
y3 2
P(3,2)
1
-3 -2 -1
o1 2 -1
3x
P3 (-3,-2)
-2
P1 (3,-2)
-3
； ；
．
分析问题 探索新知
对称点的坐标特征：
设点P(a,b)为平面上的任意一点
（1）点P(a,b)关于x轴的对称点的坐标为 (a,-b)
（2）点P(a,b)关于y轴的对称点的坐标为 (-a,b) （3）点P(a,b)关于原点O 的对称点的坐标为 (-a,-b)
关于原点O对称点的坐标________
分析问题 探索新知
f (x) x2
y
p′
p
o
x
如果沿着y轴对 折，那么对折后y轴
两侧的图像完全重 合，即函数图像上 任意一点P关于y轴 的对称点P′仍然在 函数图像上，这时 称函数图像关于y轴 对称．
y轴叫做这个函 数图像的对称轴．
f (x) x2
（X∈R）
3、点P(3，2)关于原点0的对称点是线段OP绕 着原点0旋转180°，得到与点P相重合的点P3， 点P3的坐标是多少？点P与点P3的坐标有什么 特征?
分析问题 探索新知
(1)点P(3,2)关于x 轴的对称点是点P1，其坐标为
(2)点P(3,2)关于y 轴的对称点是点P2，ቤተ መጻሕፍቲ ባይዱ坐标为
(3)点P(3,2)关于原点O 的对称点是点P3，其坐标为
1
已知函数g(x)= 2 x2-3的右半 部分图像，请你画出左半部分图 像。
y
1
D’ 2
D
C’ 1 2
B’
A’
1C
2
o
1
2B
A M
x
数形结合真的很 重要哦！
拓 展 问 题 注重应用
根据下列函数图像判断函数是否为偶函数
（1）
（2）
（3）
（4）
回归问题 归纳小结
1、对称点的坐标特征
2、函数关于y轴对称的定义
函数的奇偶性
(第1课时)
郧西职业技术学校 殷先梅
创设情景 引入新知
创设情境 引入新知
自学教材P49页，回答下列问题：
1、点P(2，3)关于x轴对称点是沿着x轴对折， 得到与点P相重合的点P1，点P1的坐标是多少？ 点P与点P1的坐标有什么特征？
2、点P(3，2)关于y轴对称点是沿着y轴对折， 得到与点P相重合的点P2，点P2的坐标是多少？ 点P与点P2的坐标有什么特征？
解决问题 深化定义
偶函数的图像性质：关于y轴对称
函数是偶函数
函数图像关于y轴对称
解决问题 深化定义
例2：判断下列函数是否为偶函数？
① f(x)=2x2+1
② f(x)= x
解决问题 深化定义
归纳：
判断一个函数是否是偶函数的基本方法及步骤是： 1、定义法： 第一步：求出函数的定义域 第二步: 判断函数的定义域是否关于原点对称 第三步：若函数定义域关于原点对称，则通过计算看f(-x) 是否等于f(x)。若函数定义域不关于原点对称则不是偶函数
y
(-a,b)
b
P(a ，b)
-a
0
a
x
(-a,-b)
-b
(a,-b)
分析问题 探索新知
例1
（1）点P（-2,3)关于x轴的对称点的坐标________
（2）点P（x，y)关于y轴的对称点的坐标________ 关于原点O的对称点的坐标________
（3）在函数y=f（x)的图象上任取一点P（a，f（a）） 点 P（a，f（a））关于y轴的对称点的坐标 ________
延伸问题 课后探究
2、思考：已知函数f（x）是偶函数，而且 在（0，+∞）上是减函数，判断f（x）在（∞，0）的单调性。
设函数f(x)的定义域为数集D， 如果对于任意的x∈D，都有-x∈D 且f(-x)=f(x),则函数f(x)叫做偶函数。
-x
x
满足两个条件：
-x∈D o x∈D x
1、对于任意的x∈D，都有-x∈ D
即函数的定义域关于原点对称
2、 f(-x)=f(x)
函数的定义域关于原点
对称，是判断偶函数的
必要条件。
研究问题
y
4
3
2
形成定义
当x1=1, x2=-1时， f(-1)=f(1).
当x1=2, x2=-2时, f(-2)=f(2).
1
对定义域内任意x，
f(-x)=f(x).
-3
-2 x -1 0
1 x2
3x
x
…… -3 -2 -1 0 1 2 3 ……
f(x)
……
9 4 1 0 1 4 9 ……
偶函数的定义：
3、偶函数的定义：设函数f(x)的定义域为数集D， 如果对于任意的x∈D，都有-x∈D，并且f(-x)= -f(x), 那么称f(x)是偶函数。偶函数的图像关于y轴对称。
4、判断偶函数的两种方法：定义法（代数法） 图像法（几何法）
5、数形结合的思想
延伸问题 课后探究
1、设计：某幼师班的学生，在美术课堂上，老师为培养学生 的审美情趣，设计了一个活动会标的一部分图案，若你是该班 的学生，请你从美学的角度合理设计图案把它补充完整。