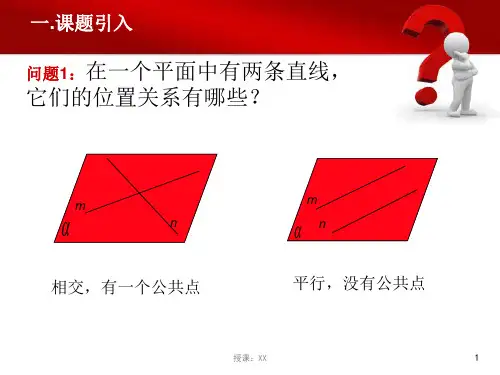
异面直线有关概念异面直线是几何学中的重要概念，是指在三维空间中不在同一个平面上且永不相交的两条直线。
本文将对异面直线的定义、性质和应用进行探讨。
1. 异面直线的定义异面直线是指两条直线位于三维空间中不在同一个平面上的情况，且永不相交。
具体而言，如果两条直线在三维空间中不平行，并且它们的法向量也不共线，则可以判断它们是异面直线。
2. 异面直线的性质2.1 异面直线不平行由于异面直线不在同一个平面上，所以它们不可能平行。
这是异面直线与平面直线的一个重要区别。
2.2 异面直线没有交点由于异面直线不相交，所以它们不存在交点。
这一性质与平面直线不同，平面直线在同一个平面内一定会相交或平行。
2.3 异面直线的距离在几何学中，两条直线之间的距离通常定义为它们之间最短的长度。
对于异面直线，可以通过求解两条直线之间的最短距离来衡量它们的远近。
3. 异面直线的应用3.1 空间几何问题在许多空间几何问题中，涉及到不同平面上的直线之间的关系。
而异面直线正是这种问题的典型例子。
通过研究异面直线的性质和特点，可以帮助解决一些空间几何问题，如直线的相交情况、距离计算等。
3.2 三维图形的建模在计算机图形学中，三维模型的建模是一个重要的研究方向。
异面直线常常用于描述和构建复杂的三维模型。
例如，通过定义不同平面上的直线，可以打造出各种形状的物体，如建筑、汽车、人物等，使它们更加真实和立体。
3.3 直线的投影问题异面直线还可以应用于直线的投影问题中。
在三维空间中，当一条直线被投影到不同的平面上时，可能会出现相交或平行的情况。
通过研究异面直线的性质和投影关系，可以更好地分析和解决直线的投影问题。
总结：异面直线是指在三维空间中不在同一个平面上且永不相交的两条直线。
它们具有不平行、没有交点和可以计算距离的性质。
异面直线在空间几何问题、三维图形的建模以及直线的投影问题中具有广泛的应用。
通过深入研究异面直线的性质和特点，可以更好地理解和解决与三维空间相关的几何问题。
