苏教版六上第六单元百分数的整理与复习 原创,思维导图,超链接
- 格式:ppt
- 大小:689.50 KB
- 文档页数:18


第六单元百分数(一)思维导图重难点梳理典例解析典例1(易错题)①判断:39m=39%m()100m是一个具体数量,不能改写成百分数。
百分数不能表示具解析39100体数量,后面不能带单位名称。
解答×②判断:甲数比乙数多25%,乙数比甲数少25%。
()解析两个数的差量相同,但单位“1”的量不同,多(少)的百分比也就不能相同,甲数比乙数多25%,乙数应比甲数少20%。
相同的差量和不同的标准量相比较,结果不同;两个不同的数和同一个标准量比较,结果也不同。
解答×③判断:一种商品,先提价10%,再降价10%,此商品的现价与原价相同。
()解析把此商品的原价看作单位“1”,假设原价是1,提价后的价格为:1×(1+10%)=1.1;降价后的价格为1.1×(1-10%)=0.99 0.99<1,所以此商品的现价小于原价。
解答×典例2(运用百分数的特点解决分数相关问题)指出下面各分数哪些可以用百分数表示。
(1)预计到2050年,我国60岁及60岁以上的老年人口约占总人口的31100。
(2)1袋食盐的质量是50100kg。
(3)李伯伯家的果园今年大丰收,今年的产量是去年的120100。
解析(1)31100表示60岁以60岁以上的老年人口与总人口之间的倍比关系。
→可以用百分数表示。
(2)50100kg表示1袋食盐的质量。
→不可以用百分数表示。
(3)120100表示今年的产量与去年的产量之间的倍比关系。
→可以用百分数表示。
表示两个量的倍比关系的分数可以用百分数表示;带有单位名称分数表示的是一个数量,不能用百分数表示。
解答(1)中的31100和(3)中的120100可以用百分数表示。
典例3 (百分率问题)教材P85第10题(1)油菜籽的出油率是42%。
2100kg油菜籽可榨油多少千克?(2)油菜籽的出油率是42%。
一个榨油厂榨出2100kg菜籽油,用了多少千克油菜籽?解析(1)油菜籽的质量×出油率=可榨油的质量(2)菜籽油的质量÷出油率=油菜籽的质量求一个数的百分之几是多少,用乘法解答,列式为:一个数×百分率=百分率的对应量;已知一个数的百分之几是多少,求这个数,用除法或列方程解答,用除法列式为:百分率对应的量÷百分率=单位“1”的量。


第7讲百分数的应用(思维导图+学问梳理+例题精讲+易错专练)一、思维导图二、学问点梳理学问点一:百分数的应用(一)1.确定单位“1”的方法:与哪个量相比,那个量就是单位“1”。
2.求一个数比另一个数多(或少)百分之几的方法:(1)先求一个数比另一个数多(或少)的具体量,再除以单位“1”的量,即两数差量÷单位“1”的量;(2)把另一个数看作单位“1”,即100%。
学问点二:百分数的应用(二)1.求“比一个数增加(削减)百分之几的数是多少”的方法:方法一:先求出增加(削减)部分的具体数量,然后用单位“1”所对应的具体数量加上(减去)增加(削减)部分的具体数量。
方法二:先求出增加(削减)后的数量是单位“1”的百分之几,然后用单位“1”所对应的具体数量乘这个百分数。
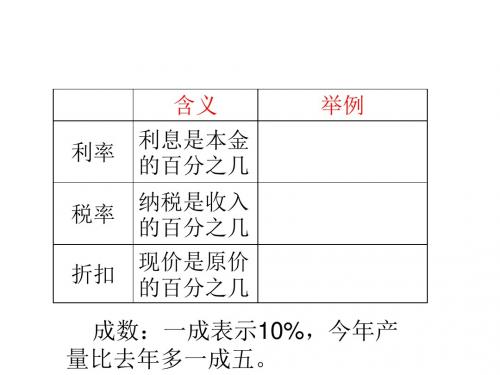
2.成数的意义。
在工农业生产和日常生活中经常用到成数,成数可以表示各行各业的进展变化状况。
“几成”就是格外之几,也就是百分之几十。
3.解决成数问题的方法。
解决成数的问题,关键是先将成数转化为百分数,然后依据百分数问题的解法进行解答。
学问点三:百分数的应用(三)1.已知两个部重量的差(和)及两个部重量对应的百分数,求总量,这类问题用方程解有两种方法:(1)A%x±B%x=两个部重量的差(和);(2)(A%±B%)x=两个部重量的差(和)。
(x代表总量;A%代表较大的部重量所占的百分数;B%代表较小的部重量所占的百分数)2.用方程解“已知比一个数增加百分之几的数是多少,求这个数”的问题有两种解答方法:(1)单位“1”的量×(1+比单位“1”多的百分率)=已知量;(2)单位“1”的量+单位“1”的量×比单位“1”多的百分率=已知量。
3.用方程解“已知一个部重量占总量的百分之几及另一个部重量,求总量”的问题有两种解答方法:(1)总量×(1-已知部重量占总量的百分率)=另一部重量;(2)总量-总量×已知部重量占总量的百分率=另一部重量。

苏教版六年级上册数学第六单元知识点整理苏教版六年级上册数学第六单元学问点整理百分数应用题是小升初必考题目之一,我们先学习好苏教版六年级上册数学第六单元百分数的学问点吧。
下面是我为大家整理的关于苏教版六年级上册数学第六单元学问点,欢迎大家来阅读。
苏教版六年级上册数学第六单元学问点百分数百分数的意义及读写:1.百分数的意义:表示一个数是另一个数的百分之几的数叫做百分数,也叫百分比或百分率。
2.百分数的读写:百分数不写成分数形式,先写分子,再写百分号。
注:百分数后面不带单位名称。
(常消失在推断题中)百分数与小数的互化:百分数与分数的互化:求一个数是另一个数的百分之几的实际问题:公式:(一个数÷另一个数)×100%生活中常见的一些百分率:合格率=合格产品数÷产品总数×100%出勤率=实际出勤人数÷应出勤人数×100%发芽率=发芽种子数÷试验种子总数×100%成活率=成活棵数÷种植总棵数×100%出油率=油的重量÷油料重量×100%命中率=命中次数÷总次数×100%及格率=及格人数÷参与考试人数×100%纳税问题:求应纳税额实际上就是求一个数的百分之几是多少,也就是把应当纳税部分的总收入乘以税率百分之几,就求出了应纳税额。
利息问题:利息=本金×利率×存期折扣问题:折扣=实际售价÷原售价×100%列方程解决稍简单的百分数实际问题:1.解答稍简单的百分数应用题和稍简单的分数应用题的解题思路、解题方法完全相同。
2.用字母或含有字母的式子表示题中两个未知的数量,找出数量间的相等关系。
依据求一个数的百分之几是多少用乘法列方程求解,或者依据除法的意义,直接解答。
3.“已知比一个数多(少)百分之几的数是多少,求这个数”的实际问题,可以依据数量间的相等关系列方程求解;或者依据除法的意义,直接解答。
六年级上册数学第六单元知识点(苏教版)百分数的意义及读写:1.百分数的意义:表示一个数是另一个数的百分之几的数叫做百分数,也叫百分比或百分率。
2.百分数的读写:百分数不写成分数形式,先写分子,再写百分号。
注:百分数后面不带单位名称。
(常出现在判断题中)百分数与小数的互化:百分数与分数的互化:求一个数是另一个数的百分之几的实际问题:公式:(一个数÷另一个数)×100%生活中常见的一些百分率:合格率=合格产品数÷产品总数×100%出勤率=实际出勤人数÷应出勤人数×100%发芽率=发芽种子数÷试验种子总数×100%成活率=成活棵数÷种植总棵数×100%出油率=油的重量÷油料重量×100%命中率=命中次数÷总次数×100%及格率=及格人数÷参加考试人数×100%纳税问题:求应纳税额实际上就是求一个数的百分之几是多少,也就是把应该纳税部分的总收入乘以税率百分之几,就求出了应纳税额。
利息问题:利息=本金×利率×存期折扣问题:折扣=实际售价÷原售价×100%列方程解决稍复杂的百分数实际问题:1.解答稍复杂的百分数应用题和稍复杂的分数应用题的解题思路、解题方法完全相同。
2.用字母或含有字母的式子表示题中两个未知的数量,找出数量间的相等关系。
根据求一个数的百分之几是多少用乘法列方程求解,或者根据除法的意义,直接解答。
3.“已知比一个数多(少)百分之几的数是多少,求这个数”的实际问题,可以根据数量间的相等关系列方程求解;或者根据除法的意义,直接解答。
4.灵活运用本单元所学知识,解决稍复杂的百分数实际问题,沟通分数、百分数应用题之间的联系。
【】。
六年级数学上册《百分数》知识点整理(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(六年级数学上册《百分数》知识点整理(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为六年级数学上册《百分数》知识点整理(word版可编辑修改)的全部内容。
六年级数学上册《百分数》知识点整理第六单元、百分数(一)一、百分数的意义:表示一个数是另一个数的百分之几的数叫做百分数。
百分数又叫百分比或百分率,百分数不能带单位。
注意:百分数是专门用来表示一种特殊的倍比关系的,表示两个数的比。
1、百分数和分数的区别和联系:(1)联系:都可以用来表示两个量的倍比关系。
(2)区别:意义不同:百分数只表示倍比关系,不表示具体数量,所以不能带单位。
分数不仅表示倍比关系,还能带单位表示具体数量.百分数的分子可以是小数,分数的分子只可以是整数。
注意:百分数在生活中应用广泛,所涉及问题基本和分数问题相同,分母是100的分数并不是百分数,必须把分母写成“%"才是百分数,所以“分母是100的分数就是百分数”这句话是错误的。
“%”的两个0要小写,不要与百分数前面的数混淆。
一般来讲,出勤率、成活率、合格率、正确率能达到100%,出米率、出油率达不到100%,完成率、增长了百分之几等可以超过100%。
一般出粉率在70%、80%,出油率在30%、40%。
2、小数、分数、百分数之间的互化(1)百分数化小数:小数点向左移动两位,去掉“%”.62222(2)小数化百分数:小数点向右移动两位,添上“%”。
(3)百分数化分数:先把百分数写成分母是100的分数,然后再化简成最简分数。