25.2求锐角的三角比的值

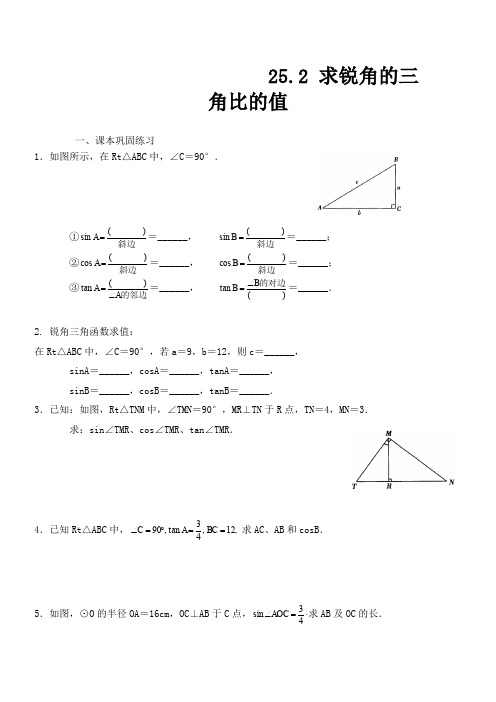
25.2 求锐角的三角比的值一、课本巩固练习1．如图所示，在Rt △ABC 中，∠C ＝90°．①斜边)(sin =A ＝______， 斜边)(sin =B ＝______； ②斜边)(cos =A ＝______，斜边)(cos =B ＝______；③的邻边A A ∠=)(tan ＝______，)(tan 的对边B B ∠=＝______．2. 锐角三角函数求值：在Rt △ABC 中，∠C ＝90°，若a ＝9，b ＝12，则c ＝______，sinA ＝______，cosA ＝______，tanA ＝______， sinB ＝______，cosB ＝______，tanB ＝______．3．已知：如图，Rt △TNM 中，∠TMN ＝90°，MR ⊥TN 于R 点，TN ＝4，MN ＝3．求：sin ∠TMR 、cos ∠TMR 、tan ∠TMR ．4．已知Rt △ABC 中，,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cosB ．5．如图，⊙O 的半径OA ＝16cm ，OC ⊥AB 于C 点，⋅=∠43sin AOC 求AB 及OC 的长．二、基础过关1．在Rt△ABC 中，∠ C＝90°，若BC ＝1，tanA 的值为A． C ．12D ．2 2．在△ABC 中，∠C=90°，sinA=53，那么tanA 的值等于（ ）.A ．35 B. 45 C. 34 D. 433、.如图，O ⊙是ABC △的外接圆，AD 是O ⊙的直径，若O ⊙的半径为32，2AC =，则sin B 的值是（ ） A ．23 B ．32 C ．34 D ．434、 如图6，沿AE 折叠矩形纸片ABCD ，使点D 落在BC 边的点F 处．已知8AB =，10BC =，AB=8,则tan EFC ∠的值为 ( )A ．34 B ．43C ．35D ．455、如图7，在等腰直角三角形ABC ∆中，90C ∠=︒，6AC =，D 为AC 上一点，若1tan 5DBA ∠= ，则AD 的长为( )A．2 C ．1 D．6、如图，直径为10的⊙A 经过点(05)C ，和点(00)O ，，与x 轴的正半轴交于点D ，二、填空题1、如图，角α的顶点为O ，它的一边在x 轴的正半轴上，另一边OA 上有一点P （3，4），则sin α= ．2、如图，菱形ABCD 的边长为10cm ，DE⊥AB，3sin 5A =，则这个菱形的面积= cm 2．三、解答题1．已知：如图，Rt △ABC 中，∠C ＝90°．D 是AC 边上一点，DE ⊥AB 于E 点．DE ∶AE ＝1∶2．求：sinB 、cosB 、tanB ．2、在Rt △ABC 中，∠C=90°，AC=8，∠A 的平分线AD=3316求 ∠B 的度数及边BC 、AB 的长.DABC4、已知：如图，在△ABC 中，∠BAC ＝120°，AB ＝10，AC ＝5．求：sin ∠ABC 的值．5、如图，在Rt△ABC 中，∠BAC=90°，点D 在BC 边上，且△ABD 是等边三角形．若AB=2，求△ABC 的周长．（结果保留根号）6．已知：如图，△ABC 中，AB ＝9，BC ＝6，△ABC 的面积等于9，求sinB ．7、写出下列特殊角的三角函数值。

第二十五章 锐角三角比（P59-P82）1． 内容目录第一节：锐角的三角比（Ⅱ）25.1 锐角的三角比的意义； 25.2 求锐角的三角比的值。

第二节：解直角三角形（Ⅲ）25.3 解直角三角形； 25.4 解直角三角形的应用。

2．中考考纲要求（1）理解锐角三角比的概念。

（2）会求特殊锐角（30°、45°、60°）的三角比的值。

（3）会用计算器求锐角的三角比的值；能根据锐角三角比的值，利用计算器求锐角的大小。

（4）会解直角三角形。

（5）理解仰角、俯角、坡度、坡角等概念，并能解决有关的实际问题。

3．重点和难点 重点是应用锐角三角比的意义及运用解直角三角形的方法进行有关几何计算。

难点是解直角三角形的应用。

4．知识结构框架图表5. 知识点1、 锐角的三角比（1） 定义：在直角三角形ABC 中，A 为一锐角，则∠A 的正弦=A a sin A=c∠的对边，即斜边∠A 的余弦=A b cos A=c∠的邻边，即斜边,∠A 的正切=A a tanA=A b∠的对边，即∠的邻边∠A 的余切=A a =A b∠的邻边，即cotA ∠的对边注：三角函数值是一个比值．定义的前提是有一个角为直角，故如果题目中无直角条件时，应设法构造一个直角。

若A ∠为一锐角，则sinA,cosA,tanA,cotA 的取值范分别是：0sinA<1,0<cosA<1,tanA>0,cotA>0<。

同一个锐角的正切和余切值互为倒数，即：1tanA cotA=1tanA=cot A或2、 特殊锐角的三角比的值（1） 特殊锐角（30°，45°，60°）的三角比的值（2） 同角，互余的两角多的三角比之间的关系：倒数关系：1tanA=cot A平方关系：22sin A+cos A=1 积商关系：sin cos tanA=,cot cos sin A A A AA=余角和余函数的关系：如果090A B ∠+∠=，那么sinA=cosB, tanA=cotB （正弦和余弦，正切和余切被称为余函数关系）。

《求锐角的三角比的值》讲义一、锐角三角比的定义在直角三角形中，锐角的三角比包括正弦（sin）、余弦（cos）、正切（tan）。

正弦（sin）等于锐角的对边与斜边的比值；余弦（cos）等于锐角的邻边与斜边的比值；正切（tan）等于锐角的对边与邻边的比值。

例如，在一个直角三角形 ABC 中，∠C 为直角，∠A 为锐角，其对边为 a，邻边为 b，斜边为 c。

那么，sin A ＝ a ／ c，cos A ＝ b ／ c，tan A ＝ a ／ b。

二、特殊锐角的三角比值我们先来了解一些特殊锐角（30°、45°、60°）的三角比值，这些是需要大家牢记的。

1、 30°角对于 30°角的直角三角形，假设斜边为 2，对边为 1，根据勾股定理可得邻边为√3。

所以，sin 30°＝ 1 ／ 2，cos 30°＝√3 ／ 2，tan 30°＝√3 ／ 3。

2、 45°角在等腰直角三角形中，两个直角边相等，假设直角边为 1，斜边为√2。

则 sin 45°＝ cos 45°＝√2 ／ 2，tan 45°＝ 1。

3、 60°角与30°角相对应，60°角的直角三角形中，假设斜边为2，邻边为1，对边为√3。

所以，sin 60°＝√3 ／ 2，cos 60°＝ 1 ／ 2，tan 60°＝√3。

三、利用三角函数定义求三角比值当已知直角三角形的边长时，我们可以直接根据三角比的定义来求出相应锐角的三角比值。

例如，在直角三角形中，∠C 为直角，∠A 为锐角，已知∠A 的对边为 4，邻边为 3，斜边为 5。

则 sin A ＝ 4 ／ 5，cos A ＝ 3 ／ 5，tanA ＝ 4 ／ 3。

再比如，一个直角三角形的斜边为 10，一个锐角的对边为 6，那么这个锐角的正弦值就是 6 ／ 10 ＝ 3 ／ 5。

第一节锐角的三角比§25.2求锐角的三角比的值教学目标(1)经历用几何方法探求特殊锐角的三角比的值的过程，掌握特殊锐角的三角比的值。

(2)会利用计算器求锐角的三角比的值，也能根据锐角的三角比的值求锐角的大小。

教学重点让学生经历用几何方法探求特殊锐角的三角比值的过程，掌握特殊锐角的三角比的值。

让学生学会利用计算器求锐角的三角比的值以及根据锐角的三角比的值求锐角的大小。

知识概要1.求特殊锐角的三角比的值，一般步骤是：(1)将直角三角形的某边长设为a，用a的代数式表示其他两边的长；(2)根据三角比的定义求值。

2.3.①如果两角互余，那么其中一个角的正切值(正弦值)与另一个角的余切值(余弦值)相等；②以030角、045角、060角为序，正切值和正弦值从小到大，余切值和余弦值则从大到小；③1=；④2为分母构成的数。

4.利用计算器求三角比的值时，先要选定“角度模式”(DEG)。

如果按MODE键一次屏幕未显示出“Deg Rad Gra”画面，那么反复按MODE键，直到显示为止。

然后按1键，计算器即进入了DEG 模式。

计算器的型号较多，应该参阅其使用说明书进行具体操作。

5.在DEG模式下，根据三角比函数名计算。

如：计算0sin25，按sin 2 5 =屏幕会显示结果。

如要计算余切，利用1cottanαα=求cotα。

如：计算0cot75，依次按1 ÷ tan 7 5 =即可；也可以依次按tan 7 5 =1x-=。

6.当角的大小涉及到“分”和(或)“秒”时，输入“度”“分”和“秒”后，必须按0’”键。

在求0sin2718''时，7.如果一个锐角的三角比的值，这个锐角就是确定的。

如果这个三角比的值不是特殊角的三角比的值，可以利用计算器计算锐角度数的近似值。

如：已知cot 1.3025α=，求锐角α。

可以依次按键： SHIFT tan -1 ( 1 ÷ 1.3025 ) = SHIFT 0’”经典题型解析(一)特殊锐角三角比例1.(1)计算：200020sin 45cos60tan 60cos 30-+⋅。

《25.2（1）求特殊锐角三角比的值》教学反思教学目标的确定：（1）经历用几何方法探求特殊锐角的三角比的值的过程,掌握特殊锐角的三角比的值.（2）能熟练计算含有30°、45°、60°角的三角比的运算式.（3）体验数形结合的数学方法和自主探究获得知识的学习过程。

教学过程的实施：1.通过练习复习锐角三角比的概念，了解学生掌握概念的情况，同时为今天的学习做铺垫。

2.由两个特殊的直角三角形中边和角的数量特征引出今天的课题，体现数形结合思想的应用。

3.先有教师推导推导45o角的三角比，意在起示范作用，在有学生自主、合作探索30°和60°角的三角比，进一步体会数形结合的数学方法和自主探索获得知识的学习过程，4.举例应用，并让学生自主探寻三角比的12个数值的规律，总结交流。

在学习特殊锐角三角比这节课时，意在让学生理解特殊锐角三角比的产生过程，并记住这些角的三角比值，并会实行简单运算。

课堂上我先和学生一起推导了30︒角的三角比，意在起示范作用；再由学生自主探索45︒和60︒角的三角比，进一步体会数形结合的数学方法和自主探索获得知识的学习过程。

因为学生基础薄弱，所以在探索45︒和60︒角的三角比时困难较多。

怎样调动起学生学习的积极性，让学生主动参与到学习中来，使教学目标得到落实，考虑到找12个数值的规律比较简单，适合我班学生探索学习，所以我引导学生探索12个数值记忆的规律，并组织学生合作交流,，慢慢地课堂也表现出了愉悦和谐的教学情境。

使学生对学习数学知识的兴趣逐渐提升。

学生通过独立思考，相互讨论、释疑解难。

从学习的被动者转变为学习的主动者，从被动接受知识变成主动探索、合作探索，并在合作交流活动中每个学生都积极参与讨论，将自己的观点、想法告诉其他同学，同时倾听其他同学的意见。

最后在师生小结中，学生在更深层次上理解了所学的内容，真正理解和掌握了基本的知识和技能（12个数值）、数学思想和方法。

数学九年级上 第二十五章 锐角三角比25.2 求锐角的三角比的值（1）一、选择题1.在Rt △ABC 中，AD 是斜边BC 上的高,如果BC=a, B β∠=,那么AD 等于 ( )A. 2sin a β⋅B. 2cos a β⋅ C. sin cos a ββ D. sin tan a ββ 2. 已知Rt △ABC 中，∠C ＝90°，AC ＝2，BC ＝3，那么下列各式中，正确的是（ ）A ．2tan 3B = B ．2cot 3B =C ．2sin 3B =D ．2cos 3B = 3. 已知点P （tan45°,-cos30°）,则P 点关于原点的对称点P ’的坐标是 （ ）A. )21,1(-- B. )21,1(- C. )23,1(-- D. )23,1(- 4、已知：是锐角，23sin =α，则等于 （ ）A. 30°B. 45°C. 60°D. 90°5、在Rt △ABC 中，∠C ＝90°，∠A ＝30°，那么B A sin sin +等于 （ ）A. 1B. 231+C. 221+D. 43 6、已知：c b a ,,是△ABC 的三边，并且关于的方程02)(222=++++c ab x b a x 有两个相等实根，则△ABC 形状是 （ ）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定。

二、填空题7、已知：α为锐角，1tan =α，则α=____________度。

8、已知：α为锐角，3sin 2=α，则____________。

9、若3)20tan(3=︒-α，则锐角α=____________。

10、α为锐角，且关于x 的方程0sin 222=+-αx x 有两个相等的实数根，则α为____________度。

11. 在△ABC 中,若tan 12A B +=,则C ∠= . 12. 计算: 2sin 604cos303tan 60-+= .13.在△ABC 中,如果AB=那么C ∠的度数为 .14.设α为锐角,则cos 1α-= .15.在△ABC 中, A ∠,B ∠均为锐角,且2tan (2sin 0B A +=,则△ABC 的形状是 .16. 在正方形ABCD 中，∠ABD 的余弦值等于________．17. 已知 α是锐角，，且sin cos αα=，则α＝ 度。

沪教版数学九年级上学期一课一练、单元测试卷和参考答案目录第二十四章相似三角形24.1放缩与相似形（1） 3 24.2 比例线段（1） 6 24.3三角形一边的平行线第一课时（1） 10 24.3三角形一边的平行线第二课时（1） 14 24.3三角形一边的平行线第三课时（1） 19 24.3三角形一边的平行线第四课时（1） 22 24.4相似三角形的判定第一课时（1） 25 24.4相似三角形的判定第二课时（1） 29 24.4相似三角形的判定第三课时（1） 33 24.4相似三角形的判定第四课时（1） 37 24.5相似三角形的性质第一课时（1） 43 24.5相似三角形的性质第二课时（1） 47 24.5相似三角形的性质第三课时（1） 52 24.6实数与向量相乘第一课时（1） 57 24.7向量的线性运算第一课时（1） 62 九年级(上)数学第二十四章相似三角形单元测试卷一 67 第二十五章锐角三角比25.1锐角三角比的意义（1） 72 25.2求锐角的三角比的值（1） 75 25.3 解直角三角形（1） 7925.4 解直角三角形的应用（1） 84 九年级(上)数学第二十五章锐角的三角比单元测试卷一 90 第二十六章二次函数26.1 二次函数的概念（1） 9426.2 特殊二次函数的图像第一课时（1） 98 26.2 特殊二次函数的图像第二课时（1） 102 26.2 特殊二次函数的图像第三课时（1） 106 26.3二次函数y=ax2+bx+c的图像第一课时（1） 111 26.3二次函数y=ax2+bx+c的图像第二课时（1） 116 26.3二次函数y=ax2+bx+c的图像第三课时（1） 121 九年级(上)数学第二十六章二次函数单元测试卷一 126 参考答案 132数学九年级上第二十四章相似三角形24.1放缩与相似形（1）一、选择题1下列各组图形中一定是相似三角形的是（）A. 两个等腰三角形B. 两个直角三角形C. 一个角为30 的等腰三角形D. 两个等边三角形2下列各组图形中一定是相似多边形的是（）A. 两个平行四边形B. 两个正方形C. 两个矩形D. 两个菱形3某两地的实际距离为3000米，画在地图上的距离是15厘米，则在地图上的距离与实际的距离之比是（）A 1:200B 1:2000C 1:20 000D 1:200 0004. 下列不一定是相似形的是（）A. 边数相同的正多边形B. 两个等腰直角三角形C. 两个圆D. 两个等腰三角形5. 下列给出的图形中，是相似形的是（）A. 三角板的、外三角形B. 两孪生兄弟的照片C. 行书中的“中”楷书中的“中”D. 同一棵树上摘下的两片树叶6. 下列各组图形中，一定是相似多边形的是（）A. 两个直角三角形B. 两个平行四边形C. 两个矩形D. 两个等边三角形7下列图形中，相似的有（）①放大镜下的图片与原来图片；②幻灯的底片与投影在屏幕上的图像③天空中两朵白云的照片④用同一底片洗出的两大小不同的照片A. 4组B. 3组C. 2组D. 1组8. 对一个图形进行放缩时，下列说确的是（）A. 图形中线段的长度与角的大小都保持不变B. 图形中线段的长度与角的大小都会改变C. 图形中线段的长度保持不变，角的大小可以改变D. 图形中线段的长度可以改变，角的大小都保持不变二、填空题9. ABC ∆与'''A B C ∆相似，则它们的对应角，对应边。

锐角三角比公式锐角三角比1. 什么是锐角三角比锐角三角比是三角函数中的一个概念，用于描述一个锐角的正弦、余弦和正切值。

在数学中，锐角是指小于90度的角。

锐角三角比可以帮助我们计算和描述锐角的各种属性。

2. 锐角三角比的相关公式下面是锐角三角比的几个常用公式：正弦（Sine）正弦值表示一个角度的对边与斜边的比值：sin(A) = 对边 / 斜边余弦（Cosine）余弦值表示一个角度的邻边与斜边的比值：cos(A) = 邻边 / 斜边正切（Tangent）正切值表示一个角度的对边与邻边的比值：tan(A) = 对边 / 邻边3. 示例解释为了更好地理解锐角三角比的概念和应用，我们来看几个示例。

示例 1假设有一个锐角三角形，其中角A的对边长度为5，邻边长度为12，斜边长度为13。

我们可以利用正弦、余弦和正切公式来计算角A 的锐角三角比值：sin(A) = 5 / 13 ≈cos(A) = 12 / 13 ≈tan(A) = 5 / 12 ≈示例 2现在假设有一个锐角三角形，其中角B的对边长度为7，邻边长度为24，斜边长度为25。

我们可以同样利用锐角三角比公式计算角B 的值：sin(B) = 7 / 25 =cos(B) = 24 / 25 =tan(B) = 7 / 24 ≈通过以上示例，我们可以看到锐角三角比可以帮助我们计算角度的各种属性，如角度的正弦、余弦和正切值。

这些值在许多数学和科学领域中都有广泛的应用，如物理、工程、地理等。

总结本文介绍了锐角三角比的概念和相关公式，并通过示例解释了如何计算锐角的正弦、余弦和正切值。

锐角三角比在数学中具有重要的应用价值，它可以帮助我们计算和描述锐角的各种属性。

在实际问题中，了解锐角三角比可以帮助我们更好地理解和解决各种角度相关的计算和测量问题。