整式的乘法、平方差公式、完全平方公式、整式的除法(B卷)

整式乘除知识点在数学的学习中，整式乘除是一个重要的部分，它不仅是后续学习代数运算的基础，也在解决实际问题中有着广泛的应用。

下面就让我们一起来深入了解整式乘除的相关知识点。

一、整式的乘法（一）单项式乘以单项式法则：把它们的系数、相同字母的幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

例如：3x²y × 5xy³＝ 15x³y⁴（二）单项式乘以多项式法则：用单项式去乘多项式的每一项，再把所得的积相加。

例如：2x(3x² 5x ＋ 1) ＝ 6x³ 10x²＋ 2x（三）多项式乘以多项式法则：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

例如：（x ＋ 2)（x 3) ＝ x² 3x ＋ 2x 6 ＝ x² x 6二、整式的除法（一）单项式除以单项式法则：把系数、同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。

例如：18x⁴y³z² ÷ 3x²y²z ＝ 6x²yz（二）多项式除以单项式法则：先把这个多项式的每一项分别除以这个单项式，然后把所得的商相加。

例如：（9x³y 18x²y²＋ 3xy³) ÷ 3xy ＝ 3x² 6xy ＋ y²三、乘法公式（一）平方差公式（a ＋ b)（a b) ＝ a² b²例如：（3x ＋ 2)（3x 2) ＝ 9x² 4（二）完全平方公式（a ＋ b)²＝ a²＋ 2ab ＋ b²（a b)²＝ a² 2ab ＋ b²例如：（x ＋ 5)²＝ x²＋ 10x ＋ 25四、整式乘除的应用（一）几何图形中的应用在求解长方形、正方形等图形的面积和周长时，经常会用到整式的乘除。

整式的运算法则整式的加减法：（1）去括号；（2）合并同类项。

整式的乘法：),(都是正整数n m a a a n m n m +=•),(都是正整数）（n m a a m n n m =)()(都是正整数n b a ab n n n = 22))((b a b a b a -=-+ 2222)(b ab a b a ++=+ 2222)(b ab a b a +-=-整式的除法：)0,,(≠=÷-a n m a a a n m n m 都是正整数【注意】（1）单项式乘单项式的结果仍然是单项式。

（2）单项式与多项式相乘，结果是一个多项式，其项数与因式中多项式的项数 相同。

（3）计算时要注意符号问题，多项式的每一项都包括它前面的符号，同时还要 注意单项式的符号。

（4）多项式与多项式相乘的展开式中，有同类项的要合并同类项。

（5）公式中的字母可以表示数，也可以表示单项式或多项式。

（6）),0(1);0(10为正整数p a a a a a p p ≠=≠=-（7）多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加，单项式除以多项式是不能这么计算的。

一、选择（每题2分，共24分） 1．下列计算正确的是（ ）．A ．2x 2·3x 3=6x 3B ．2x 2+3x 3=5x 5C ．（－3x 2）·（－3x 2）=9x 5D ．54x n ·25x m =12x m+n2．一个多项式加上3y 2－2y －5得到多项式5y 3－4y －6，则原来的多项式为（ ）． A ．5y 3+3y 2+2y －1 B ．5y 3－3y 2－2y －6 C ．5y 3+3y 2－2y －1 D ．5y 3－3y 2－2y －1 3．下列运算正确的是（ ）．A ．a 2·a 3=a 5B ．（a 2）3=a 5C ．a 6÷a 2=a 3D ．a 6－a 2=a 4 4．下列运算中正确的是（ ）．A．12a+13a=15a B．3a2+2a3=5a5C．3x2y+4yx2=7 D．－mn+mn=0二、填空（每题2分，共28分）6．－xy2的系数是______，次数是_______．8．x_______=x n+1；（m+n）（______）=n2－m2；（a2）3·（a3）2=______．9．月球距离地球约为3.84×105千米，一架飞机速度为8×102千米/时， 若坐飞机飞行这么远的距离需_________．10．a2+b2+________=（a+b）2a2+b2+_______=（a－b）2（a－b）2+______=（a+b）211．若x2－3x+a是完全平方式，则a=_______．12．多项式5x2－7x－3是____次_______项式．三、计算（每题3分，共24分）13．（2x2y－3xy2）－（6x2y－3xy2）14．（－32ax4y3）÷（－65ax2y2）·8a2y17．（x－2）（x+2）－（x+1）（x－3）18．（1－3y）（1+3y）（1+9y2）19．（ab+1）2－（ab－1）2四、运用乘法公式简便计算（每题2分，共4分）20．（998）221．197×203五、先化简，再求值（每题4分，共8分）22．（x+4）（x－2）（x－4），其中x=－1．23．[（xy+2）（xy－2）－2x2y2+4]，其中x=10，y=－1 25．六、解答题（每题4分，共12分）24．已知2x+5y=3，求4x·32y的值．25．已知a2+2a+b2－4b+5=0，求a，b的值．幂的运算一、同底数幂的乘法（重点）1.运算法则：同底数幂相乘,底数不变，指数相加。

七年级数学下---平方差、完全平方公式专项练习题平方差：一、选择题1 平方差公式(a+b) (a—b) =a2—b2中字母a, b表示()A •只能是数B •只能是单项式C •只能是多项式D•以上都可以2•下列多项式的乘法中，可以用平方差公式计算的是( )1 12 2A . (a+b) (b+a)B . ( —a+b) (a—bC . (一a+b) (b—- a)D . (a —b) (b +a)3 33. 下列计算中，错误的有( )A. 1个B . 2个C .3个D .4个©( 3a+4) (3a —4) =9a2—4；购(2a2—b) (2a2+b) =4a2—b2;@(3 —x) (x+3) =x2—9; ④(—x+y) • (x+y) =—(x—y) (x+y) =—x2—y2.4 .若x2—y2=30，且x —y= —5,则x+y 的值是()A.5 B .6 C . —6 D . —5二、填空题：5、(a+b—1) (a—b+1) = ( ____ ) 2—( _____ )2.6 . ( —2x+y) ( —2x —y) = _. 7. ( —3x2+2y2) ( ____ )=9x4—4y4.8.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积，差是_________ .三、计算题9.利用平方差公式计算：20- x 211. 10 .计算：(a+2) (a2+4) (a4+16) (a —2).3 3B卷：提高题1 .计算：(1) (2+1) (22+1) (24+1)-( 22n+1) +1 (n 是正整数)；4016(2) (3+1) (32+1) ( 34+1)-( 32008+1)3 .解方程：x (x+2) + (2x+1) (2x - 1) =5 (x 2+3).4. 广场内有一块边长为2a 米的正方形草坪，经统一规划后，南北方向要缩短长3米，则改造后的长方形草坪的面积是多少?5. 下列运算正确的是()A . a 3+a 3=3a 6 B . (-a ) 3 •( — a ) 5=-a 8C . (-2a 2b ) • 4a=-24a 6b 3D . (- ^a -4b ) (1 a -4b ) =16b 2--a 2 3396. 计算：(a+1) (a -1) = ______ . C 卷：课标新型题2231.(规律探究题)已知 x 工 1，计算(1+x ) (1-x ) =1 — x ， (1 — x ) (1+x+x ) =1 — x ，234(1-x ) (?1+x+x+x ) =1 — x .(1)观察以上各式并猜想：(1—x ) (1+x+x 2+…+x n ) =_ . (n 为正整数)(2) 根据你的猜想计算：①(1 — 2) (1+2+Z+23+24+25) = ______ . ②2+22+23+…+2n = _____ (n 为正整数).99989722 .式计算：2009X 2007- 20082.(1)计算:2007220072008 2006(2)计算:20072 2008 2006 13米，东西方向要加③(x—1) (x +x +x + …+x +x+1) = ________ .(3) 通过以上规律请你进行下面的探索：2 2®(a — b ) (a+b ) = ____________ . ®(a — b ) (a+ab+b ) = ______________ . @( a — b ) (a 3+a 2b+ab 2+b 3) =_ .2.(结论开放题)请写出一个平方差公式，使其中含有字母m n 和数字4. __________________完全平方公式变形的应用完全平方式常见的变形有：a 2 b 2 (a b)2 2ab ； a 2 b 2 (ab)2 2ab2 2 2 2 2 2(a b ) (a b) 4ab ; a b c (a b c) 2ab 2ac 2bc1 已知 m+n 2-6m+10n+34=0 求 m+n 的值y 2 4x 6y 13 0, X 、y 都是有理数，求x y 的值练一练A 组:1 .已知(a b) 5,ab 3 求(a b)2 与 3(a 2 b 2)的值。

七年级数学下-—-平方差、完全平方公式专项练习题平方差：一、选择题1．平方差公式(a+b）(a－b）=a2－b2中字母a，b表示（）A．只能是数 B．只能是单项式 C．只能是多项式 D．以上都可以2．下列多项式的乘法中，可以用平方差公式计算的是（）A．（a+b）(b+a） B．（－a+b)(a－b C．(13a+b）（b－13a） D．（a2－b)(b2+a）3．下列计算中，错误的有（） A．1个 B．2个 C．3个 D．4个①（3a+4）（3a－4）=9a2－4；②(2a2－b）（2a2+b）=4a2－b2；③(3－x）(x+3)=x2－9；④（－x+y）·（x+y）=－（x－y）（x+y)=－x2－y2．4．若x2－y2=30,且x－y=－5，则x+y的值是（ )A．5 B．6 C．－6 D．－5二、填空题: 5、(a+b－1）（a－b+1）=（_____）2－（_____）2．6．（－2x+y）（－2x－y)=______．7．（－3x2+2y2）（______)=9x4－4y4．8．两个正方形的边长之和为5,边长之差为2，那么用较大的正方形的面积减去较小的正方形的面积,差是_____．三、计算题9．利用平方差公式计算：2023×2113． 10．计算：（a+2)（a2+4）(a4+16）（a－2）．B卷：提高题1．计算：（1）（2+1）（22+1)(24+1)…（22n+1）+1（n是正整数）；（2)（3+1）（32+1）（34+1）…（32008+1）－401632．2．式计算：2009×2007－20082． 3．解方程：x（x+2）+（2x+1）（2x－1）=5（x2+3)．（1）计算：22007200720082006-⨯．（2）计算：22007200820061⨯+．4．广场内有一块边长为2a米的正方形草坪，经统一规划后，南北方向要缩短3米，东西方向要加长3米，则改造后的长方形草坪的面积是多少？5．下列运算正确的是( ） A．a3+a3=3a6 B．（－a）3·（－a）5=－a8C．(－2a2b）·4a=－24a6b3 D．（－13a－4b)（13a－4b）=16b2－19a26．计算：（a+1)（a－1）=______．C卷:课标新型题1．（规律探究题）已知x≠1,计算（1+x）（1－x）=1－x2，（1－x）(1+x+x2)=1－x3，（1－x)（•1+x+x2+x3）=1－x4．（1）观察以上各式并猜想：（1－x）（1+x+x2+…+x n)=_____ _．（n为正整数）（2）根据你的猜想计算:①（1－2）（1+2+22+23+24+25)=______．②2+22+23+…+2n=______（n为正整数）．③（x－1）（x99+x98+x97+…+x2+x+1)=_______．①（a －b ）（a+b ）=_______ ． ②(a －b ）（a 2+ab+b 2）=_____ _． ③（a －b)（a 3+a 2b+ab 2+b 3）=____ __．2．（结论开放题)请写出一个平方差公式,使其中含有字母m,n 和数字4．完全平方公式变形的应用完全平方式常见的变形有:ab b a b a 2)(222-+=+；ab b a b a 2)(222+-=+ab b a b a 4)(22=--+）（； bc ac ab c b a c b a 222)(2222---++=++1、已知m 2+n 2—6m+10n+34=0，求m+n 的值2、已知0136422=+-++y x y x ，y x 、都是有理数,求y x 的值。

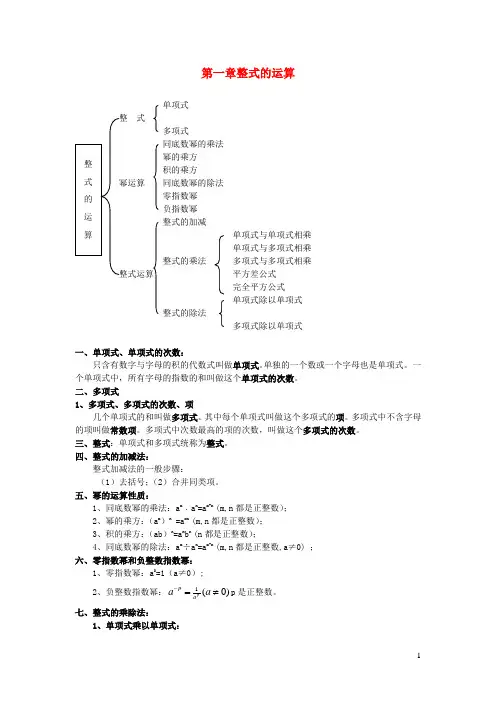
第一章整式的运算单项式 整 式多项式同底数幂的乘法幂的乘方 积的乘方幂运算 同底数幂的除法零指数幂负指数幂 整式的加减单项式与单项式相乘单项式与多项式相乘整式的乘法 多项式与多项式相乘整式运算 平方差公式完全平方公式单项式除以单项式整式的除法多项式除以单项式一、单项式、单项式的次数：只含有数字与字母的积的代数式叫做单项式。

单独的一个数或一个字母也是单项式。

一个单项式中，所有字母的指数的和叫做这个单项式的次数。

二、多项式1、多项式、多项式的次数、项几个单项式的和叫做多项式。

其中每个单项式叫做这个多项式的项。

多项式中不含字母的项叫做常数项。

多项式中次数最高的项的次数，叫做这个多项式的次数。

三、整式：单项式和多项式统称为整式。

四、整式的加减法：整式加减法的一般步骤：（1）去括号；（2）合并同类项。

五、幂的运算性质：1、同底数幂的乘法：a m ﹒a n =a m+n (m,n 都是正整数）；2、幂的乘方：（a m ）n =a mn (m,n 都是正整数）；3、积的乘方：（ab ）n =a n b n (n 都是正整数）；4、同底数幂的除法：a m ÷a n =a m-n (m,n 都是正整数,a ≠0) ；六、零指数幂和负整数指数幂：1、零指数幂：a 0=1（a ≠0）;2、负整数指数幂：1(0)p p a a a -=≠p 是正整数。

七、整式的乘除法：1、单项式乘以单项式：整 式 的 运 算法则：单项式与单项式相乘，把它们的系数、p 是正整数相同字母的幂分别相乘，其余的字母连同它的指数不变，作为积的因式。

2、单项式乘以多项式：法则：单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加。

3、多项式乘以多项式：多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

4、单项式除以单项式：单项式相除，把系数、同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。

完全平方式平方差公式整式乘除综合计算30题一.解答题（共30小题）1.多项式x2+l加上一个整式后是含X的二项式的完全平方式.例题：X2+l+= （x+l）2.（1）按上例再写出两个加上一个单项式后是含X的二项式的完全平方式的式子（不能用已知的例题）:①x?+l+ _____________ =（X - 1）2;（2）X2+1+=（尹+1）2.（2）按上例写出一个加上一个多项式后是一个含X的二项式的完全平方式x2+l+= （x2+l）2.2.己知a2 - 4a+4+9b2+6b+l=0,求a、b 的值.3.己知x口-3二0，求值: X(2)IX4.如果a2-2 （k- 1） ab+9b2是一个完全平方式，那么k=5.关于x的二次三项式：x2+2mx+4 - m2是一个完全平方式，求m的值.6.（2002・岳阳）用简便方法计算：W2X98+4 .2522 - 24827.计算；(1) (x - 3y) (x-^y)；(2)4x2 - ( - 2x+3) ( - 2x - 3).8.(a - 2b+c) (a+2b - c).9.利用乘法公式计算：(1)(2x - 3y) 2 - (y+3x) (3x - y)；(2)(x+y) (x2+y2) (x - y) (x4+y4):(3)(a - 2b+3) (a+2b-3)；(4)[ (x - y) 24- (x+y) 2] (x2 - y2)；(5)(m - n - 3) 2.10.计算（1）（-2X2(2)(x m-y n) (x,n+y n)；(3)(3)2 Sb) 2；(4)(x+y+z) 2.11.计算：(1) (5m - 6n) ( - 6n - 5m)； (2) (—x2y2+3m) ( - 3m+—x2y2).2 212.计算：(x - y) 2 - (x+y) (x - y)13 .计算：(1)(2x - 1) (4X2+1)(2X+1)；(2)(2a - b+3) (2a - 3+b)；(3) 4 (a+2) 2-7 (a+3) (a- 3) +3 (a- 1) 2.14.计算(1)(^a2b3) • ( - 15a2b2)3(2)(lx2y - 2xy+y2) ・2xy(3)(2x+3) (3x+4)(4)(3x+7y) (3x - 7y)(5)(x-3y) 2(6)(x+5y) 215.利用乘法公式计算⑴(-x2+2y2)2⑵ (4+2y ) 2+ (4-2y) 2 乙乙(3)(a+3b) (a - 3b)(4)( - 4a - 1) (4a- 1)(5)9982(6)62x5816.( - 6xy2z+8x2y3) + ( - 6xy)17.[ ( - 4a2b3) 2 - 6a4b4x ( - 0.5ab3)]《(-2ab2) 318.计算下列各题：(1)( -4a5b3)之+ (8a2b3)(2)(x+2) 2- (x+3) (x-3)(3)[ (2x+l) (4x+2) - 2]。

初中数学整式的乘除与因式分解知识点归纳一、整式的乘法：1.普通整式相乘：将每一项的系数相乘，同时将每一项的指数相加。

2.平方整式相乘：先将每一项平方，再将每一项相乘得到结果。

3.完全平方的平方差公式：(a-b)(a+b)=a²-b²。

4. 公式展开：通过公式展开可求两个或多个整式的乘积，例如(a+b)²=a²+2ab+b²。

二、整式的除法：1.整式相除的概念：整式A除以整式B，若存在整式C，使得B×C=A，那么C称为A除以B的商式。

2.用辗转相除法进行整式的除法计算。

三、因式分解：1.抽象公因式法：将多项式中的每一项提取出公因式，然后将剩下的部分合并。

2.公式法：运用一些常用的公式，如平方差公式、完全平方公式等进行因式分解。

3.分组法：将多项式中的项进行分组，使每一组都有一个公因式，然后进行合并。

4. 二次三项式的因式分解：对于二次三项式a²+2ab+b²或a²-2ab+b²，可以因式分解为(a±b)²。

5.因式定理和余式定理：若(x-a)是多项式P(x)的因式，则P(a)=0。

根据这一定理可以找到多项式的因式。

四、常见整式的因式分解：1.平方差公式：a²-b²=(a+b)(a-b)。

2. 完全平方公式：a²+2ab+b²=(a+b)²，a²-2ab+b²=(a-b)²。

3. 符号"相反"公式：a²-2ab+b²=(b-a)²。

4. 三项平方公式：a³+b³=(a+b)(a²-ab+b²)，a³-b³=(a-b)(a²+ab+b²)。

5. 公因式公式：a²+ab=a(a+b)。

七年级整式知识点总结一、整式的基本概念1、单项式定义：由数与字母的积组成的代数式叫做单项式，单独的一个数或一个字母也叫做单项式。

系数：单项式中的数字因数叫做这个单项式的系数。

次数：单项式中所有字母的指数的和叫做这个单项式的次数。

2、多项式定义：几个单项式的和叫做多项式。

项：在多项式中，每个单项式叫做多项式的项。

次数：多项式中次数最高的项的次数，叫做这个多项式的次数。

二、整式的运算1、整式的加减同类项：所含字母相同，并且相同字母的指数也相同的项叫做同类项。

合并同类项：把同类项合并成一项叫做合并同类项。

合并同类项时，把同类项的系数相加，字母和字母的指数不变。

去括号法则：括号前是“＋”，把括号和它前面的“＋”去掉后，原括号里各项的符号都不改变；括号前是“”，把括号和它前面的“”去掉后，原括号里各项的符号都要改变。

2、整式的乘法单项式乘以单项式：把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

单项式乘以多项式：用单项式去乘多项式的每一项，再把所得的积相加。

多项式乘以多项式：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

3、整式的除法单项式除以单项式：把系数、同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。

多项式除以单项式：先把这个多项式的每一项分别除以单项式，再把所得的商相加。

三、幂的运算1、同底数幂的乘法：底数不变，指数相加，即＼（a^m ＼timesa^n ＝ a^｛m+n}＼）。

2、幂的乘方：底数不变，指数相乘，即＼（（a^m)＾n ＝ a^｛mn}＼）。

3、积的乘方：先把积中的每一个因数分别乘方，再把所得的幂相乘，即＼（（ab)＾n ＝ a^n b^n\）。

4、同底数幂的除法：底数不变，指数相减，即＼（a^m ＼div a^n＝ a^｛mn}＼）（＼（a ＼neq 0\））。

四、整式乘法公式1、平方差公式：＼（（a ＋ b)（a b) ＝ a^2 b^2\）2、完全平方公式：＼（（a ＼pm b)＾2 ＝ a^2 ＼pm 2ab ＋ b^2\）五、整式的应用1、利用整式表示实际问题中的数量关系。

整式知识点归纳整式是代数式的重要组成部分，也是数学学习中的基础内容之一。

下面就来对整式的相关知识点进行一个全面的归纳。

一、整式的定义整式为单项式和多项式的统称，是有理式的一部分，在有理式中可以包含加、减、乘、除、乘方五种运算，但在整式中除数不能含有字母。

单项式是由数与字母的积组成的代数式，单独的一个数或一个字母也叫做单项式。

例如，5、a、2xy 等都是单项式。

多项式是由有限个单项式的代数和组成的代数式。

例如，2x ＋3y、a² 2ab ＋ b²等都是多项式。

二、整式的分类1、单项式系数：单项式中的数字因数叫做单项式的系数。

例如，单项式 5x的系数是 5。

次数：单项式中所有字母的指数和叫做单项式的次数。

例如，单项式 3x²y 的次数是 3（2 ＋ 1 ＝ 3）。

2、多项式项：在多项式中，每个单项式叫做多项式的项。

其中不含字母的项叫做常数项。

例如，多项式 2x²＋ 3x 1 中，2x²、3x、－1 是项，－1 是常数项。

次数：多项式里，次数最高项的次数，就是这个多项式的次数。

例如，多项式 x³ 2x²＋ 5 中，次数最高项是 x³，次数为 3，所以这个多项式的次数是 3。

三、整式的运算1、整式的加减去括号法则：括号前是“＋”号，把括号和它前面的“＋”号去掉后，原括号里各项的符号都不改变；括号前是“”号，把括号和它前面的“”号去掉后，原括号里各项的符号都要改变。

合并同类项：同类项的系数相加，所得的结果作为系数，字母和字母的指数不变。

2、整式的乘法单项式乘以单项式：系数相乘作为积的系数，相同字母的幂分别相乘，对于只在一个单项式中出现的字母，则连同它的指数一起作为积的一个因式。

单项式乘以多项式：用单项式乘以多项式的每一项，再把所得的积相加。

多项式乘以多项式：先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加。

3、整式的除法单项式除以单项式：把系数、同底数幂分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。

完全平方公式和平方差公式的应用公式：语言叙述：两数的。

公式结构特点：左边：右边：熟悉公式：公式中的a和b既可以表示数字也可以表示字母，还可以表示一个单项式或者一个多项式。

(5+6x)(5-6x)中是公式中的a，是公式中的b(5+6x)(-5+6x)中是公式中的a，是公式中的b(x-2y)(x+2y)填空：1、(2x-1)( )=4x2-12、(-4x+ )( -4x)=16x2-49y2第一种情况：直接运用公式1.（a+3）(a-3)2..( 2a+3b)(2a-3b)3. (1+2c)(1-2c)4. (-x+2)(-x-2)第二种情况：运用公式使计算简便1、1998×20022、498×5023、999×10014、1.01×0.995、30.8×29.26、（100-13）×（99-23）7、（20-19）×（19-89）第三种情况：两次运用平方差公式1、（a+b）(a-b)(a2+b2)2、(a+2)(a-2)(a2+4)3、(x-12)(x2+14)(x+12)第四种情况：需要先变形再用平方差公式1、（-2x-y）(2x-y)2、(y-x)(-x-y) 3.(-2x+y)(2x+y) 4.(4a-1)(-4a-1) 5.(b+2a)(2a-b) 6.(a+b)(-b+a) 7.(ab+1)(-ab+1)第五种情况：每个多项式含三项1.（a+2b+c ）(a+2b-c)2.(a+b-3)(a-b+3)3.x-y+z)(x+y-z)4.(m-n+p)(m-n-p)完全平方公式公式：语言叙述：两数的 . 。

公式结构特点：左边： 右边：熟悉公式：公式中的a 和b 既可以表示数字也可以表示字母，还可以表示一个单项式或者一个多项式。

公式变形1、a 2+b 2=(a+b)2 =(a-b)22、（a-b ）2=(a+b)2 ; (a+b)2=(a-b)23、(a+b)2 +（a-b ）2=4、(a+b)2 --（a-b ）2= 一、计算下列各题： 1、2)(y x + 2、2)23(y x - 3、2)21(b a + 4、2)12(--t5、2)313(c ab +-6、2)2332(y x +7、2)121(-x 8、(0.02x+0.1y)2二、利用完全平方公式计算： （1）1022 （2）1972三、计算： （1）22)3(x x -+ （2）22)(y x y +-（3）()()2()x y x y x y --+-四、计算：（1）)4)(1()3)(3(+---+a a a a （2）22)1()1(--+xy xy（3）)4)(12(3)32(2+--+a a a五、计算：（1）)3)(3(-+++b a b a （2）)2)(2(-++-y x y x（3）)3)(3(+---b a b a （4）()()2323x y z x y z +-++六、拓展延伸 巩固提高 1、若22)2(4+=++x k x x，求k 值。