专题复习-“隐形圆”问题

专题13隐圆问题3种模型通用的解题思路：隐圆一般有如下呈现方式：（1）定点定长：当遇到同一个端点出发的等长线段时，通常以这个端点为圆心，等线段长为半径构造辅助圆；（2）定弦定角：当遇到动点对定点对定线段所张的角为定值时，通常把张角转化为圆周角构造辅助圆。

当遇到直角时，通常以斜边为直径构造辅助圆。

（3）四点共圆：对角互补的四边形的四个顶点共圆。

隐圆常与线段最值结合考查。

类型1：定点定长1．（2023•新城区校级三模）圆的定义：在同一平面内，到定点的距离等于定长的所有点所组成的图形．（1）已知：如图1，OA OB OC∠=︒，则ACB∠=AOB==，请利用圆规画出过A、B．C三点的圆．若7035︒．如图，Rt ABCAB=．∠=︒，2BCA∆中，90∠=︒，30ABC（2）已知，如图2．点P为AC边的中点，将AC沿BA方向平移2个单位长度，点A、P、C的对应点分别为点D、E、F，求四边形BDFC的面积和BEA∠的大小．（3）如图3，将AC边沿BC方向平移a个单位至DF，是否存在这样的a，使得直线DF上有一点Q，满足45∠=︒且此时四边形BADF的面积最大？若存在，求出四边形BADF面积的最大值及平移距离a，BQA若不存在，说明理由．【分析】（1）利用圆的定义知A，B，C三点共圆，再利用圆周角定理求解．（2）根据图形的平移性质，判定平移后图形形状，继而确定面积的计算方式和方法，角度问题也迎刃而解．（3）因角度不变，借助圆周角定点在圆周上运动时角度不变的思想，判断出D点能够向右移动的最大距离，求出四边形的最大面积．【解答】（1）以O 为圆心，OA 为半径作辅助圆，如图，，70AOB ∠=︒ ，35ACB ∴∠=︒，故答案为35︒．（2）连接PB ，PE ，如图，，Rt ABC ∆中，90ABC ∠=︒，30BCA ∠=︒，2AB =．4AC ∴=，60BAC ∠=︒，BC =．P 为Rt ABC ∆斜边AC 中点，122BP AC ∴==，线段AC 平移到DF 之后，2AB AD PE ===，2BP AE ==，∴四边形ABPE 为菱形，60BAC ∠=︒ ，30BEA ∴∠=︒，//CF BD ，且90ABC ∠=︒，∴四边形BDFC 为直角梯形，11()622S BD CF BC ∴=+⨯=⨯⨯=（3）如图所示，以AB 为斜边在AB 的右侧作等腰直角三角形OAB ，以O 为圆心，OA 为半径作O ，当AC 边沿BC 方向平移a 个单位至DF 时，满足45BQA ∠=︒且此时四边形BADF 的面积最大，∴直线DF 与O 相切于点Q ，连接OQ 交AD 于G ，过点O 作OH AD ⊥于H ，则90AHO OHG DQG ∠=∠=∠=︒，45OAH ∠=︒，30GDQ ∠=︒，90ABC ∠=︒ ，30BCA ∠=︒，2AB =，BC ∴=OA OB OQ ===1AH OH ∴==，33HG =，233OG =，3GQ ∴=，23DG GQ ==-，11AD AH HG GD ∴=++=++，1a ∴=+，此时直角梯形ABFD 的最大面积为：11()112222S BF AD AB =⨯+⨯=⨯++-++⨯=+．【点评】本题主要考查图形的平移，圆心角，圆周角之间的关系，解题的关键是数形结合，找到极值点求解．2．（2024•兰州模拟）综合与实践【问题情境】在数学综合实践课上，“希望小组”的同学们以三角形为背景，探究图形变化过程中的几何问题，如图，在ABC ∆中，AB AC =，90BAC ∠=︒，点D 为平面内一点（点A ，B ，D 三点不共线），AE 为ABD ∆的中线．【初步尝试】（1）如图1，小林同学发现：延长AE 至点M ，使得ME AE =，连接DM ．始终存在以下两个结论，请你在①，②中挑选一个进行证明：①DM AC =；②180MDA DAB ∠+∠=︒；【类比探究】（2）如图2，将AD 绕点A 顺时针旋转90︒得到AF ，连接CF ．小斌同学沿着小林同学的思考进一步探究后发现：12AE CF =，请你帮他证明；【拓展延伸】（3）如图3，在（2）的条件下，王老师提出新的探究方向：点D 在以点A 为圆心，AD 为半径的圆上运动()AD AB >，直线AE 与直线CF 相交于点G ，连接BG ，在点D 的运动过程中BG 存在最大值．若4AB =，请直接写出BG的最大值．【分析】（1）利用SAS 证明ABE MDE ∆≅∆，可得AB DM =，再结合AB AC =，即可证得DM AC =；由全等三角形性质可得BAE DME ∠=∠，再运用平行线的判定和性质即可证得180MDA DAB ∠+∠=︒；（2）延长AE 至点M ，使得ME AE =，连接DM ．利用SAS 证得ACF DMA ∆≅∆，可得CF AM =，再由12AE AM =，可证得12AE CF =；（3）延长DA 至M ，使AM AD =，设AM 交CF 于N ，连接BM 交CF 于K ，取AC 中点P ，连接GP ，可证得()ACF ABM SAS ∆≅∆，利用三角形中位线定理可得//AE BM ，即//AG BM ，利用直角三角形性质可得11222GP AC AB ===，得出点G 在以P 为圆心，2为半径的P 上运动，连接BP 并延长交P 于G '，可得BG '的长为BG 的最大值，再运用勾股定理即可求得答案．【解答】（1）证明：①AE 为ABD ∆的中线，BE DE ∴=，在ABE ∆和MDE ∆中，BE DE AEB MED AE ME =⎧⎪∠=∠⎨⎪=⎩，()ABE MDE SAS ∴∆≅∆，AB DM ∴=，AB AC = ，DM AC ∴=；②由①知ABE MDE ∆≅∆，BAE DME ∴∠=∠，//AB DM ∴，180MDA DAB ∴∠+∠=︒；（2）证明：延长AE 至点M ，使得ME AE =，连接DM．由旋转得：AF AD =，90DAF ∠=︒，90BAC ∠=︒ ，360DAF BAC BAD CAF ∠+∠+∠+∠=︒，180BAD CAF ∴∠+∠=︒，由（1）②得：180MDA DAB ∠+∠=︒，DM AB AC ==，CAF MDA ∴∠=∠，在ACF ∆和DMA ∆中，AF AD CAF MDA AC DM =⎧⎪∠=∠⎨⎪=⎩，()ACF DMA SAS ∴∆≅∆，CF AM ∴=，12AE AM = ，12AE CF ∴=；（3）如图3，延长DA 至M ，使AM AD =，设AM 交CF 于N ，连接BM 交CF 于K ，取AC 中点P ，连接GP ，由旋转得：AF AD =，90DAF ∠=︒，AF AM ∴=，1809090MAF ∠=︒-︒=︒，90BAC ∠=︒ ，MAF CAM BAC CAM ∴∠+∠=∠+∠，即CAF BAM ∠=∠，在ACF ∆和ABM ∆中，AC AB CAF BAM AF AM =⎧⎪∠=∠⎨⎪=⎩，()ACF ABM SAS ∴∆≅∆，AFC AMB ∴∠=∠，即AFN KMN ∠=∠，ANF KNM ∠=∠ ，90FAN MKN ∴∠=∠=︒，BM CF ∴⊥，E 、A 分别是DB 、DM 的中点，AE ∴是BDM ∆的中位线，//AE BM ∴，即//AG BM ，AG CF ∴⊥，90AGC ∴∠=︒，点P 是AC 的中点，11222GP AC AB ∴===，∴点G 在以P 为圆心，2为半径的P 上运动，连接BP 并延长交P 于G '，BG ∴'的长为BG 的最大值，在Rt ABP ∆中，BP ==2BG BP PG ∴'=+'=+，BG ∴的最大值为2+．【点评】本题是几何综合题，考查了三角形的全等的性质与判定，两直线垂直的判定，三角形中位线定理，勾股定理，圆的性质，熟练掌握全等三角形的判定定理是解决本题的关键．3．（2022•番禺区二模）已知抛物线23(0)2y ax bx a =+->与x 轴交于点A ，B 两点，OA OB <，4AB =．其顶点C 的横坐标为1-．（1）求该抛物线的解析式；（2）设点D 在抛物线第一象限的图象上，DE AC ⊥垂足为E ，//DF y 轴交直线AC 于点F ，当DEF ∆面积等于4时，求点D 的坐标；（3）在（2）的条件下，点M 是抛物线上的一点，M 点从点B 运动到达点C ，FM FN ⊥交直线BD 于点N ，延长MF 与线段DE 的延长线交于点H ，点P 为N ，F ，H 三点构成的三角形的外心，求点P 经过的路线长．【分析】（1）利用对称性，求得A 和B 的坐标，然后用待定系数法求得抛物线的解析式；（2）证明CGA ∆和DEF ∆都为等腰直角三角形，利用等面积法求得4DF =，再求得直线AC 的解析式为1y x =-，设点D 的坐标，得到点F 的坐标，然后求解即可；（3）先求得45BDF ∠=︒，推出点P 的运动路径时11H N 的中点绕点F 逆时针旋转90︒得到2N H 的中点之间的弧长，证明四边形2DN FE 为正方形，即可求解．【解答】解：（1） 点A ，点B 两点关于直线1x =-对称，4AB =，(1,0)A ∴，(3,0)B -，代入232y ax bx =+-得，30239302a b a b ⎧+-=⎪⎪⎨⎪--=⎪⎩，解得：121a b ⎧=⎪⎨⎪=⎩，∴抛物线的解析式为21322y x x =+-．（2）如图1所示：//DF y 轴//GC ，GCA DFE ∴∠=∠，抛物线的解析式为22131(1)2222y x x x =+-=+-，∴顶点(1,2)C --，(1,0)A ，2AG ∴=，2CG =，CGA ∴∆为等腰直角三角形，45GCA DFE ∴∠=∠=︒，DE AC ⊥ ，DEF ∴∆为等腰直角三角形，DE EF ∴=，DF =，142DEF S DE EF ∆=⋅= ，DE ∴=，4DF ∴==，设直线AC 的解析式为y kx b =+，则02k b k b +=⎧⎨-+=-⎩，解得：11k b =⎧⎨=-⎩，∴直线AC 的解析式为1y x =-，设点213(,22D x x x +-，则(,1)F x x -，221311(1)42222DF x x x x ∴=+---=-=，解得：3x =或3x =-（舍)，(3,6)D ∴，(3,2)F ．（3）如图2所示，NFH ∆ 是直角三角形，NFH ∴∆的外心是斜边NH 的中点，当点M 位于点B 时，△11N FH ，其外心是斜边11H N 的中点，当点M 位于点C 时，得△2N FE ，其外心是斜边22N H 的中点，即2N E 的中点，(3,6)D ，(3,0)B -，33tan 16BDF +∴∠==，45BDF ∴∠=︒，由（2）得，45FDE ∠=︒，45DBA BAC ∴∠=∠=︒，//BD AC ∴，FN BD ∴⊥，DF ∴平分BDE ∠，90BDE ∠=︒，∴点D ，N ，F ，H 四点共圆，∴点P 在线段DF 的垂直平分线上，即点P 在2N E 上运动，即点P 的运动轨迹是一条线段．2290DN F N DH DHF ∠=∠=∠=︒ ，2FN FE =，∴四边形2DN FE 为正方形，此时点P 在DF 上，且2EP =；当点M 与点C 重合时，此时点P 在DF 上，即为2P ，且222FP EP ==，由题意，224BN BD DN =-=，BF =2N F =，21//FN DH ，2BFN ∴∆∽△1BH D ，∴21BN BF BD BH =，解得1FH =，1FP ∴=，由勾股定理可得：121P P =，即点P 的运动轨迹长为1．【点评】本题主要考查二次函数的综合问题，包括待定系数法确定函数解析式，三角形外接圆的性质，弧长公式，勾股定理，三角函数解直角三角形等，理解题意，作出相应辅助线是解题的关键．4．（2021•红谷滩区校级模拟）（1）学习心得：小刚同学在学习完“圆”这一章内容后，感觉到有一些几何问题，如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．例如：如图1，在ABC=，求BDC∆外一点，且AD AC∠的度数．若∆中，AB AC=，80BAC∠=︒，D是ABC以点A 为圆心，AB 为半径作辅助圆A ，则点C 、D 必在A 上，BAC ∠是A 的圆心角，而BDC ∠是圆周角，从而可容易得到BDC ∠=40︒．（2）问题解决：如图，在四边形ABCD 中，90BAD BCD ∠=∠=︒，25BDC ∠=︒，求BAC ∠的度数．（3）问题拓展：抛物线21(1)34y x =--+与y 轴交于点A ，顶点为B ，对称轴BC 与x 轴交于点C ，点P 在抛物线上，直线//PQ BC 交x 轴于点Q ，连接BQ ．①若含45︒角的直线三角板如图所示放置，其中，一个顶点与C 重合，直角顶点D 在BQ 上，另一顶点E 在PQ 上，求Q 的坐标；②若含30︒角的直角三角板一个顶点与点C 重合，直角顶点D 在BQ 上，另一个顶点E 在PQ 上，点D 与点B ，点Q 不重合，求点P 的坐标．【分析】（1）利用同弦所对的圆周角是所对圆心角的一半求解．（2）由A 、B 、C 、D 共圆，得出BDC BAC ∠=∠，（3）①先求出抛物线顶点的坐标，再由点D 、C 、Q 、E 共圆，得出45CQB OED ∠=∠=︒，求出CQ ，再求点Q 的坐标．②分两种情况，Ⅰ、当30︒的角的顶点与点C 重合时，Ⅱ、当60︒的角的顶点与点C 重合时，运用点D 、C 、Q 、E 共圆，求出CQ 即点P 的横坐标，再代入抛物线求出点P 的纵坐标，即可求出点P 的坐标．【解答】解：（1）AB AC = ，AD AC =，∴以点A 为圆心，点B 、C 、D 必在A 上，BAC ∠ 是A 的圆心角，而BDC ∠是圆周角，1402BDC BAC ∴∠=∠=︒，（2）如图2，90BAD BCD ∠=∠=︒ ，∴点A 、B 、C 、D 共圆，BDC BAC ∴∠=∠，25BDC ∠=︒ ，25BAC ∴∠=︒，（3）①如图3点B 为抛物线21(1)34y x =--+的顶点，∴点B 的坐标为(1,3)，45︒ 角的直角三角板如图所示放置，其中，一个顶点与C 重合，直角顶点D 在BQ 上，另一顶点E 在PQ 上，∴点D 、C 、Q 、E 共圆，45CQB CED ∴∠=∠=︒，3CQ BC ∴==，4OQ ∴=，∴点Q 的坐标为(4,0)，②如图4，Ⅰ、当30︒的角的顶点与点C 重合时，直角三角板30︒角的顶点与点C 重合，直角顶点D 在BQ 上，另一个顶点E 在PQ 上∴点D 、C 、Q 、E 共圆，60CQB CED ∴∠=∠=︒，3CQ BC ∴==1OQ ∴=+，∴把1+代入21(1)34y x =--+得94y =，∴点P 的坐标是(1+94Ⅱ、如图5，当60︒的角的顶点与点C 重合时，直角三角板60︒角的顶点与点C 重合，直角顶点D 在BQ 上，另一个顶点E 在PQ 上∴点D 、C 、Q 、E 共圆，30CQB CED ∴∠=∠=︒，CQ ∴==，1OQ ∴=+∴把1+21(1)34y x =--+得154y =-，∴点P 的坐标是(1+，154-综上所述，点P 的坐标是(1+94或(1+15)4-．【点评】本题主要考查了圆的综合题，解题的关键就是运用同弦对的圆周角相等．类型2：定弦定角1．（2022•雁塔区校级三模）问题提出（1）如图①，已知ABC ∆为边长为2的等边三角形，则ABC ∆的面积为问题探究（2）如图②，在ABC ∆中，已知120BAC ∠=︒，BC =，求ABC ∆的最大面积；问题解决（3）如图③，某校学生礼堂的平面示意为矩形ABCD ，其宽20AB =米，长24BC =米，为了能够监控到礼堂内部情况，现需要在礼堂最尾端墙面CD 上安装一台摄像头M 进行观测，并且要求能观测到礼堂前端墙面AB 区域，同时为了观测效果达到最佳，还需要从点M 出发的观测角45AMB ∠=︒，请你通过所学知识进行分析，在墙面CD 区域上是否存在点M 满足要求？若存在，求出MC 的长度；若不存在，请说明理由．【分析】（1）作AD BC ⊥于D ，由勾股定理求出AD 的长，即可求出面积；（2）作ABC ∆的外接圆O ，可知点A 在 BC上运动，当A O BC '⊥时，ABC ∆的面积最大，求出A H '的长，从而得出答案；（3）以AB 为边，在矩形ABCD 的内部作一个等腰直角三角形AOB ，且90AOB ∠=︒，过O 作HG AB ⊥于H ，交CD 于G ，利用等腰直角三角形的性质求出OA ，OG 的长，则以O 为圆心，OA 为半径的圆与CD 相交，从而O 上存在点M ，满足45AMB ∠=︒，此时满足条件的有两个点M ，过1M 作1M F AB ⊥于F ，作1EO M F ⊥于E ，连接OF ，利用勾股定理求出OE 的长，从而解决问题．【解答】解：（1）作AD BC ⊥于D ，ABC ∆ 是边长为2的等边三角形，1BD ∴=，AD ∴==ABC ∴∆的面积为122⨯=；（2）作ABC ∆的外接圆O ，120BAC ∠=︒ ，BC =，∴点A 在 BC上运动，当A O BC '⊥时，ABC ∆的面积最大，60BOA '∴∠=︒，33BH CH ==，3OH ∴=，6OB =，633A H OA OH ''∴=-=-=，ABC ∴∆的最大面积为133932⨯=（3）存在，以AB 为边，在矩形ABCD 的内部作一个等腰直角三角形AOB ，且90AOB ∠=︒，过O 作HG AB ⊥于H ，交CD 于G ，20AB = 米，10AH OH ∴==米，2OA =米，24BC = 米，14OG ∴=米，10214> ，∴以O 为圆心，OA 为半径的圆与CD 相交，O ∴ 上存在点M ，满足45AMB ∠=︒，此时满足条件的有两个点M ，过1M 作1M F AB ⊥于F ，作1EO M F ⊥于E ，连接OF ，10EF OH ∴==米，1102OM =114EM ∴=米，22112OE OM M E ∴-=米，18CM BF ∴==米，同理210212CM BH OE =+=+=（米)，MC ∴的长度为8米或12米．【点评】本题是四边形综合题，主要考查了等边三角形的性质，矩形的性质，等腰直角三角形的性质，勾股定理，垂径定理等知识，熟练掌握定角定边的基本模型是解题的关键．2．（2023•灞桥区校级模拟）问题提出：（1）如图①，ABC ∆为等腰三角形，120C ∠=︒，8AC BC ==，D 是AB 上一点，且CD 平分ABC ∆的面积，则线段CD 的长度为4．问题探究：（2）如图②，ABC ∆中，120C ∠=︒，10AB =，试分析和判断ABC ∆的面积是否存在最大值，若存在，求出这个最大值；若不存在，请说明理由．问题解决：（3）如图③，2023年第九届丝绸之路国际电影开幕式在西安曲江竞技中心举行，主办方要在会场旁规划一个四边形花圃ABCD ，满足600BC =米，300CD =米，60C ∠=︒，60A ∠=︒，主办方打算过BC 的中点M 点（入口）修建一条径直的通道ME （宽度忽略不计）其中点E （出口）为四边形ABCD 边上一点，通道ME 把四边形ABCD 分成面积相等并且尽可能大的两部分，分别规划成不同品种的花圃以供影迷休闲观赏．问是否存在满足上述条件的通道ME ？若存在，请求出点A 距出口的距离AE 的长；若不存在，请说明理由．【分析】（1）由题意可知，CD 是ABC ∆的中线，利用等腰三角形的性质推出CD AB ⊥，利用三角函数求解即可解决问题；（2）当ABC ∆的AB 边上的高CD 最大时，三角形ABC 的面积最大，即CD 过圆心O ，连接AO ．求出CD 的最大值即可得出答案；（3）连接DM ，BD ．首先证明90BDC ∠=︒，求出BD ，推出BDC ∆的面积是定值，要使得四边形ABCD 的面积最大，只要ABD ∆的面积最大即可，因为BD 为定值，A ∠为定角60=︒，推出当ABD ∆是等边三角形时，求出四边形ABCD 的面积最大值，然后再求出90MDE ∠=︒，构建方程解决问题即可．【解答】解：（1）如图①，CD 平分ABC ∆的面积，AD DB ∴=，8AC BC == ，CD AB ∴⊥，1602ACD BCD ACB ∠=∠=∠=︒，cos 8cos 604CD AC ACD ∴=∠=︒=，CD ∴的长度为4，故答案为：4；（2）存在．如图②，10AB = ，120ACB ∠=︒都是定值，∴点C 在AB 上，并且当点C 在 AB 的中点时，ABC ∆的面积最大；连接OC 交AB 于点D ，则CD AB ⊥，152AD BD AB ===，1602ACD ACB ∠=∠=︒，∴tan AD ACD CD ∠=，53tan 603AD CD ==︒，∴125323ABC S AB CD ∆=⋅=，答：ABC ∆（3）存在．如图③，连接DM ，BD ，M 是BC 的中点，13002CM BC ∴==，CM CD ∴=，又60C ∠=︒ ，CMD ∴∆是等边三角形，60MDC CMD ∴∠=∠=︒，CM DM BM ==，30CBD MDB ∴∠=∠=︒，90BDC ∴∠=︒，tan 60BD CD ∴=⋅︒=米，在ABD ∆中，BD =60A ∠=︒为定值，由（2）可知当AB AD =时，即ABD ∆为等边三角形时ABD ∆的面积最大，此时也为四边形ABCD 的最大值(BDC ∆的面积不变），21330024max BDC BDA S S S ∆∆=+=⨯⨯=；ABD ∆ 是等边三角形，60ADB ∴∠=︒，90ADM ADB BDM ∴∠=∠+∠=︒，由12EMD CDM max S S S ∆∆+=，得：21130030022DE ⨯+=⨯解得：DE =，AE AD DE ∴=-==)，答：点A 距出口的距离AE 的长为米．【点评】本题是圆的综合题，考查了勾股定理，垂径定理，解直角三角形，等边三角形的判定和性质等知识，解题的关键是理解题意构造辅助圆，灵活运用所学知识解决问题，难度较大，属于中考压轴题．3．（2023•柯城区校级一模）如图，点A 与点B 的坐标分别是(1,0)，(5,0)，点P 是该直角坐标系内的一个动点．（1）使30APB ∠=︒的点P 有无数个；（2）若点P 在y 轴上，且30APB ∠=︒，求满足条件的点P 的坐标；（3）当点P 在y 轴上移动时，APB ∠是否有最大值？若有，求点P 的坐标，并说明此时APB ∠最大的理由；若没有，也请说明理由．【分析】（1）已知点A 、点B 是定点，要使30APB ∠=︒，只需点P 在过点A 、点B 的圆上，且弧AB 所对的圆心角为60︒即可，显然符合条件的点P 有无数个．（2）结合（1）中的分析可知：当点P 在y 轴的正半轴上时，点P 是（1）中的圆与y 轴的交点，借助于垂径定理、等边三角形的性质、勾股定理等知识即可求出符合条件的点P 的坐标；当点P 在y 轴的负半轴上时，同理可求出符合条件的点P 的坐标．（3）由三角形外角的性质可证得：在同圆或等圆中，同弧所对的圆周角大于同弧所对的圆外角．要APB ∠最大，只需构造过点A 、点B 且与y 轴相切的圆，切点就是使得APB ∠最大的点P ，然后结合切线的性质、三角形外角的性质、矩形的判定与性质、勾股定理等知识即可解决问题．【解答】解：（1）以AB 为边，在第一象限内作等边三角形ABC ，以点C 为圆心，AC 为半径作C ，交y 轴于点1P 、2P ．在优弧1APB 上任取一点P ，如图1，则11603022APB ACB ∠=∠=⨯︒=︒．∴使30APB ∠=︒的点P 有无数个．故答案为：无数．（2）①当点P 在y 轴的正半轴上时，过点C 作CG AB ⊥，垂足为G ，如图1．点(1,0)A ，点(5,0)B ，1OA ∴=，5OB =．4AB ∴=．点C 为圆心，CG AB ⊥，122AG BG AB ∴===．3OG OA AG ∴=+=．ABC ∆ 是等边三角形，4AC BC AB ∴===．CG ∴===∴点C 的坐标为(3，．过点C 作CD y ⊥轴，垂足为D ，连接2CP ，如图1，点C 的坐标为(3，，3CD ∴=，OD =1P 、2P 是C 与y 轴的交点，1230APB AP B ∴∠=∠=︒．24CP CA == ，3CD =，2DP ∴== 点C 为圆心，12CD PP ⊥，12PD P D ∴==2(0P ∴，-．1(0P ，+．②当点P 在y 轴的负半轴上时，同理可得：3(0,P -．4(0,P -．综上所述：满足条件的点P 的坐标有：(0，-、(0，、(0,--、(0,-+．（3）当过点A 、B 的E 与y 轴相切于点P 时，APB ∠最大．理由：可证：APB AEH ∠=∠，当APB ∠最大时，AEH ∠最大．由2sin AEH AE∠=得：当AE 最小即PE 最小时，AEH ∠最大．所以当圆与y 轴相切时，APB ∠最大．①当点P 在y 轴的正半轴上时，连接EA ，作EH x ⊥轴，垂足为H ，如图2．E 与y 轴相切于点P ，PE OP ∴⊥．EH AB ⊥ ，OP OH ⊥，90EPO POH EHO ∴∠=∠=∠=︒．∴四边形OPEH 是矩形．OP EH ∴=，3PE OH ==．3EA ∴=．90EHA ∠=︒ ，2AH =，3EA =，EH ∴===OP ∴P ∴．②当点P 在y 轴的负半轴上时，同理可得：(0,P ．理由：①若点P 在y 轴的正半轴上，在y 轴的正半轴上任取一点M （不与点P 重合），连接MA ，MB ，交E 于点N ，连接NA ，如图2所示．ANB ∠ 是AMN ∆的外角，ANB AMB ∴∠>∠．APB ANB ∠=∠ ，APB AMB ∴∠>∠．②若点P 在y 轴的负半轴上，同理可证得：APB AMB ∠>∠．综上所述：当点P 在y 轴上移动时，APB ∠有最大值，此时点P 的坐标为和(0,．【点评】本题考查了垂径定理、圆周角定理、勾股定理、等边三角形的性质、矩形的判定与性质，切线的性质、三角形外角性质等知识，综合性强．同时也考查了创造性思维，有一定的难度．构造辅助圆是解决本题关键．类型3：四点共圆1．（2022•中原区校级模拟）阅读下列材料，并完成相应的任务．西姆松定理是一个平面几何定理，其表述为：过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线，则三垂足共线（此线常称为西姆松线）．某数学兴趣小组的同学们尝试证明该定理．如图（1），已知ABC∆内接于O，点P在O上（不与点A，B，C重合），过点P分别作AB，BC，AC的垂线，垂足分别为点D，E，F．求证：点D，E，F在同一条直线上．如下是他们的证明过程（不完整）:如图（1），连接PB，PC，DE，EF，取PC的中点Q，连接QE．QF，则12EQ FQ PC PQ CQ====，（依据1)点E，F，P，C四点共圆，180FCP FEP∴∠+∠=︒．（依据2)又180ACP ABP∠+∠=︒，FEP ABP∴∠=∠．同上可得点B，D，P，E四点共圆，⋯⋯任务：（1）填空：①依据1指的是中点的定义及直角三角形斜边上的中线等于斜边的一半；②依据2指的是．（2）请将证明过程补充完整．（3）善于思考的小虎发现当点P是 BC的中点时，BD CF=，请你利用图（2）证明该结论的正确性．【分析】（1）利用直角直角三角形斜边上的中线的性质和圆内接四边形对角互补即可；（2）利用直角三角形斜边上中线的性质证明点E，F，P，C和点B，D，P，E四点分别共圆，再说明180FEP DEP∠+∠=︒，可证明结论；（3）连接PA，PB，PC，利用HL证明Rt PBD Rt PCF∆≅∆，从而得出结论．【解答】（1）解：①依据1指的是中点的定义及直角三角形斜边上的中线等于斜边的一半，②依据2指的是圆内接四边形对角互补，故答案为：①直角三角形斜边上的中线等于斜边的一半；②圆内接四边形对角互补；（2）解：如图（1），连接PB，PC，DE，EF，取PC的中点Q，连接QE．QF，则12EQ FQ PC PQ CQ ====，∴点E，F，P，C四点共圆，180FCP FEP∴∠+∠=︒，又180ACP ABP∠+∠=︒，FEP ABP∴∠=∠，同上可得点B，D，P，E四点共圆，DBP DEP∴∠=∠，180ABP DBP∠+∠=︒，180FEP DEP∴∠+∠=︒，∴点D，E，F在同一直线上；（3）证明：如图，连接PA，PB，PC，点P 是 BC的中点，∴ BPPC =，BP PC ∴=，PAD PAC ∠=∠，又PD AD ⊥ ，PF AC ⊥，PD PF ∴=，Rt PBD Rt PCF(HL)∴∆≅∆，BD CF ∴=．【点评】本题主要考查了四点共圆，以及圆内接四边形的性质，角平分线的性质，全等三角形的判定与性质等知识，证明Rt PBD Rt PCF ∆≅∆是解题的关键．2．（2021•哈尔滨模拟）（1）【学习心得】于彤同学在学习完“圆”这一章内容后，感觉到一些几何问题如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．例如：如图1，在ABC ∆中，AB AC =，90BAC ∠=︒，D 是ABC ∆外一点，且AD AC =，求BDC ∠的度数．若以点A 为圆心，AB 为半径作辅助A ，则点C 、D 必在A 上，BAC ∠是A 的圆心角，而BDC ∠是圆周角，从而可容易得到BDC ∠=45︒．（2）【问题解决】如图2，在四边形ABCD 中，90BAD BCD ∠=∠=︒，25BDC ∠=︒，求BAC ∠的度数．（3）【问题拓展】如图3，如图，E ，F 是正方形ABCD 的边AD 上两个动点，满足AE DF =．连接CF 交BD 于点G ，连接BE 交AG 于点H ．若正方形的边长为2，则线段DH 长度的最小值是．【分析】（1）利用同弦所对的圆周角是所对圆心角的一半求解．（2）由A 、B 、C 、D 共圆，得出BDC BAC ∠=∠，（3）根据正方形的性质可得AB AD CD ==，BAD CDA ∠=∠，ADG CDG ∠=∠，然后利用“边角边”证明ABE ∆和DCF ∆全等，根据全等三角形对应角相等可得12∠=∠，利用“SAS ”证明ADG ∆和CDG ∆全等，根据全等三角形对应角相等可得23∠=∠，从而得到13∠=∠，然后求出90AHB ∠=︒，取AB 的中点O ，连接OH 、OD ，根据直角三角形斜边上的中线等于斜边的一半可得112OH AB ==，利用勾股定理列式求出OD ，然后根据三角形的三边关系可知当O 、D 、H 三点共线时，DH 的长度最小．【解答】解：（1）如图1，AB AC = ，AD AC =，∴以点A 为圆心，AB 为半径作圆A ，点B 、C 、D 必在A 上，BAC ∠ 是A 的圆心角，而BDC ∠是圆周角，1452BDC BAC ∴∠=∠=︒，故答案为：45；（2）如图2，取BD 的中点O ，连接AO 、CO ．90BAD BCD ∠=∠=︒ ，∴点A 、B 、C 、D 共圆，BDC BAC ∴∠=∠，25BDC ∠=︒ ，25BAC ∴∠=︒，（3）如图3，在正方形ABCD 中，AB AD CD ==，BAD CDA ∠=∠，ADG CDG ∠=∠，在ABE ∆和DCF ∆中，AB CD BAD CDA AE DF =⎧⎪∠=∠⎨⎪=⎩，()ABE DCF SAS ∴∆≅∆，12∴∠=∠，在ADG ∆和CDG ∆中，AD CD ADG CDG DG DG =⎧⎪∠=∠⎨⎪=⎩，()ADG CDG SAS ∴∆≅∆，23∴∠=∠，13∴∠=∠，390BAH BAD ∠+∠=∠=︒ ，190BAH ∴∠+∠=︒，1809090AHB ∴∠=︒-︒=︒，取AB 的中点O ，连接OH 、OD ，则112OH AO AB ===，在Rt AOD ∆中，OD ===，根据三角形的三边关系，OH DH OD +>，∴当O 、D 、H 三点共线时，DH 的长度最小，最小值1OD OH =-=．（解法二：可以理解为点H 是在Rt AHB ∆，AB 直径的半圆 AB 上运动当O 、H 、D 三点共线时，DH 长度最小）1-．【点评】本题主要考查了圆的综合题，需要掌握垂径定理、圆周角定理、等腰直角三角形的性质以及勾股定理等知识，难度偏大，解题时，注意辅助线的作法．3．（2022•潢川县校级一模）如图1，点B 在直线l 上，过点B 构建等腰直角三角形ABC ，使90BAC ∠=︒，且AB AC =，过点C 作CD ⊥直线l 于点D ，连接AD ．（1）小亮在研究这个图形时发现，90BAC BDC ∠=∠=︒，点A ，D 应该在以BC 为直径的圆上，则ADB ∠的度数为45︒，将射线AD 顺时针旋转90︒交直线l 于点E ，可求出线段AD ，BD ，CD 的数量关系为；（2）小亮将等腰直角三角形ABC 绕点B 在平面内旋转，当旋转到图2位置时，线段AD ，BD ，CD 的数量关系是否变化，请说明理由；（3）在旋转过程中，若CD 长为1，当ABD ∆面积取得最大值时，请直接写AD 的长．【分析】（1）由90BAC ∠=︒，且AB AC =，可得45ACB ABC ∠=∠=︒，由90BAC BDC ∠=∠=︒，推出A 、B 、C 、D 四点共圆，所以45ADB ACB ∠=∠=︒；由题意知EAB DAC ∆≅∆，所以BE CD =，由AE AD =，90EAD ∠=︒，可知ADE ∆是等腰直角三角形，推出2CD DB EB BD DE +=+==；（2）如图2，将AD 绕点A 顺时针旋转90︒交直线l 于点E ．易证()EAB DAC SAS ∆≅∆，则BE CD =，由AE AD =，90EAD ∠=︒，所以ADE ∆是等腰直角三角形，则2DE =，由BD CD BD BE DE -=-=，推出BD CD-=；（3）当点D在线段AB的垂直平分线上且在AB的左侧时，ABD∆的面积最大．【解答】解：（1）①如图，在图1中．=，，且AB AC∠=︒90BACACB ABC∴∠=∠=︒，45，∠=∠=︒90BAC BDC∴、B、C、D四点共圆，A∴∠=∠=︒；45ADB ACB②由题意可知，90∠=∠=︒，EAD BAC∴∠=∠，EAB DAC又AE AD=，AB AC=，EAB DAC SAS∴∆≅∆，()∴=，BE CD，90AE AD=∠=︒，EAD∴∆是等腰直角三角形，ADE∴=，DE，+=+=CD DB EB BD DE∴+=；CD DB故答案为45︒，CD DB+=；（2）线段AD，BD，CD的数量关系会变化，数量关系为BD CD-=．理由如下：如图2，将AD绕点A顺时针旋转90︒交直线l于点E．则90∠=∠=︒，DAE CAB∴∠=∠，DAC EAB又AD AE=，AC AB=，EAB DAC SAS∴∆≅∆，()∴=，BE CD，90AE AD=∠=︒，EAD∴∆是等腰直角三角形，ADE∴=，2DE，-=-=BD CD BD BE DE∴-=；2BD CD（3）由（2）知，CDA BEA∆≅∆，∴∠=∠，CDA AEB，∠=︒DEA45∴∠=︒-︒=︒，AEB18045135∴∠=∠=︒，135CDA AEB∴∠+∠=︒+︒=︒，13545180CDA ABC∴、B、C、D四点共圆，A于是作A、B、C、D外接圆O，如图，当点D在线段AB的垂直平分线上且在AB的左侧时，DG经过圆心，此时DG最长，因此ABD∆的面积最大．作DG AB ⊥，则DG 平分ADB ∠，DB DA =，在DA 上截取一点H ，使得1CD DH ==，45ADB ACB ∠=∠=︒ ，22.5GDB ∴∠=︒，67.5DBG ∠=︒，67.54522.5DBC ∴∠=︒-︒=︒，4522.522.5HCB DHC HBC ∠=∠-∠=︒-︒=︒，HCB HBC ∴∠=∠，HB CH ∴==，1AD BD DH BH ∴==+=．【点评】本题考查三角形综合题、等腰直角三角形的性质和判定、全等三角形的判定和性质、圆等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用辅助圆解决问题，属于中考压轴题．。

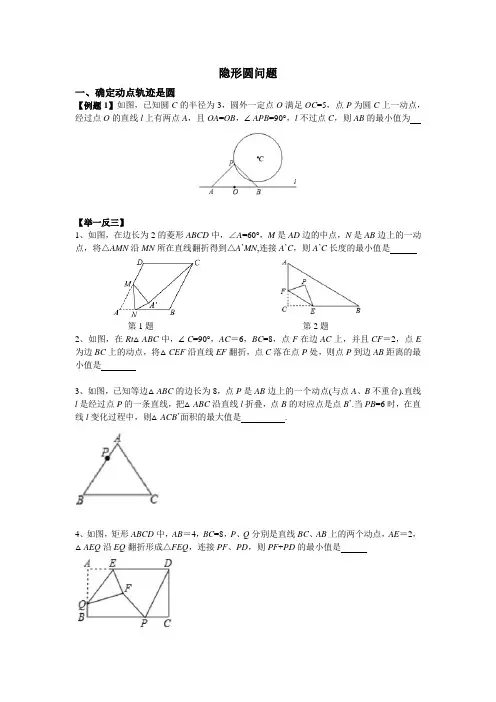
隐形圆问题一、确定动点轨迹是圆【例题1】如图，已知圆C的半径为3，圆外一定点O满足OC=5，点P为圆C上一动点，经过点O的直线l上有两点A，且OA=OB，∠APB=90°，l不过点C，则AB的最小值为【举一反三】1、如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A’MN,连接A’C，则A’C长度的最小值是第1题第2题2、如图，在Rt△ABC中，∠C=90°，AC＝6，BC=8，点F在边AC上，并且CF＝2，点E 为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是3、如图，已知等边△ABC的边长为8，点P是AB边上的一个动点(与点A、B不重合).直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.当PB=6时，在直线l变化过程中，则△ACB’面积的最大值是.4、如图，矩形ABCD中，AB＝4，BC=8，P、Q分別是直线BC、AB上的两个动点，AE＝2，△AEQ沿EQ翻折形成△FEQ，连接PF、PD，则PF+PD的最小值是二、定边对直角知识回顾:直径所对的圆周角是直角构造思路:一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧.图形释义:若AB是一条定线段，且∠APB-90°，则P点轨迹是以AB为直径的圆【例题1】已知正方形ABCD边长为2，E、F分别是BC、CD上的动点，且满足BE＝CF，连接AE、BF，交点为P点，则PC的最小值为【举一反三】1、如图，E、F是正方形ABCD的边AD上的两个动点，满足AE＝DF，连接CF交BD于点G，连接BE交AG于点H，若正方形边长为2，则线段DH长度的最小值是2、如图，Rt△ABC中，AB⊥BC，AB=6，BC＝4，P是△ABC内部的一个动点，且满足∠P AB ＝∠PBC，则线段CP长的最小值是3、如图，AB是半圆O的直径，点C在半圆O上，AB＝5，AC＝4.D是弧BC上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE.在点D移动的过程中，BE的最小值为4、如图，在Rt△ABC中，∠BAC=90°，AC＝12，AB＝10，点D是AC上的一个动点，以AD为直径作圆O，连接BD交圆O于点E，则AE的最小值为5、如图，正方形ABCD的边长为4，动点E、F分別从点A、C同时出发，以相同的速度分别沿AB、CD向终点B、D移动，当点E到达点B时，运动停止，过点B作直线EF的垂线BG，垂足为点G，连接AG，则AG长的最小值为【辅助圆+将军饮马】如图，正方形ABCD的边长是4，点E是AD边上一动点，连接BE，过点A作AF⊥BE于点F，点P是AD边上另一动点，则PC+PF的最小值为【辅助圆+相切】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AB＝4，D是BC上一动点，CE⊥AD于E，EF⊥AB交BC于点F，则CF的最大值是三、定边对定角在“定边对直角”问题中，依据“直径所对的圆周角是直角”，关键性在于寻找定边、直角，而根据圆周角定理:同圆或等圆中，同弧或等弧所対的圆周角都相.定边必不可少，而直角则可一般为定角.例如，AB为定值，∠P为定角，则P点轨迹是一个圆.当然，∠P度数也是特殊角，比如30°、45°、60°、120°，下面分别作对应的轨迹圆若∠P＝30°，以AB为边，同侧构造等边三角形AOB，O即为圆心若∠P＝45°，以AB为斜边，同侧构造等腰直角三角形AOB，O即为圆心.若∠P＝60°，以AB为底，同侧构造顶角为120°的等腰三角形AOB，O即为圆心.若∠P＝120°，以AB为底，异侧为边构造顶角为120°的等腰三角形AOB，O即为圆心.【例题1】如图，等边△ABC边长为2，E、F分別是BC、CA上两个动点，且BE=CF，连接AE、BF，交点为P点，则CP的最小值为【举一反三】1、如图，△ABC为等边三角形，AB=3，若P为△ABC内一动点，且满足∠P AB＝∠ACP，则线段PB长度的最小值为2、在△ABC中，AB＝4，∠C＝60°，∠A>∠B，则BC的长的取值范围是3、如图，AB是圆O的直径，M、N是弧AB(异于A、B)上两点，C是弧MN上一动点，∠ACB 的角平分线交圆O于点D，∠BAC的平分线交CD于点E，当点C从点M运动到点N时，则C、E两点的运动路径长的比是。

专题：隐形的圆——“道是无圆却有圆”方法技巧常见的隐圆有两类：(1)到定点的距离等于定长的点在同一个圆上(圆的定义)；(2)若定长线段的张角是定角(定弦定角)，则定角的顶点在定弦所对的一条弧上运动．利用“辅助圆”的丰富性质转换角，求线段的长或最值是隐圆类问题的基本模式．题型一利用“定点定长”构隐圆【例1】如图，在 ABCD中，AB＝4，BC＝3，∠ABC＝60°，点E为平面内的一动点，点P为CE的中点，若AE＝1，求BP的最大值．【例2】如图，O是长度为4的线段AB上的一点，且OA＝1，以OA为半径作⊙O，点M是⊙O上的一动点，连接MB，以MB为腰作等腰Rt△MBC，使∠MBC＝90°(M，B，C三点为逆时针顺序)，连接AC．求AC长度的取值范围．题型二 利用“定弦定角”构隐圆【例3】如图，在正方形ABCD 中，AC ，BD 是对角线，点P 为对角线BD 上的一点，作PE ⊥AP 交BC 于点E ．若∠CAE ＝15°，求PBPE的值．【例4】如图，⊙O 的半径为1，AB 为⊙O 的弦，将弦AB 绕点A 逆时针旋转120°，得到AC ，连接OC ，求OC 长度的最大值．针对练习61．如图，已知AB 是⊙O 的直径，CD 是⊙O 的弦(CD 与AB 不平行)，点M 是CD 的中点，CE ⊥AB 于点E ，DF ⊥AB 于点F ．①当∠EMF ＝60°时，求CDAB的值；②当∠EMF ＝90°时，CD AB 的值为 ；当∠EMF ＝120°时，CDAB的值为 ．AC上的一动点，PEAB上的一点，且∠AOC＝120°，点P是⌒2．如图，AB是半圆⊙O的直径，点C是⌒⊥OA于点E，PF⊥OC于点F，CD⊥OB于点D，求证：EF＝CD．3．如图，在四边形ABCD中，∠DAB＝∠ABC＝90°，AD＝AB＝1，BC＝2，点P为射线DA上的一动点，过B，D，P三点的圆交PC于点Q．求DQ的最小值．4．如图，△ABC的两个顶点A，B在半径为6的⊙O上，∠A＝30°，∠B＝90°，点C在⊙O内．当点A在圆上运动，且OC的长最小时，求弦AB的长．。

隐形圆(4大模型与6类题型)第一部分【模型梳理与题型目录】隐形圆模型是初中数学中的重要知识点，常用于解决一些看似没有直接使用圆的知识但实际上需要运用圆的性质来解决的问题，隐形圆常常用于解决最值问题.本专题梳理了隐形圆四大模型，供大家参考使用.【模型1】 定点定长模型【模型分析】(1)出现共端点、等线段时，可以利用圆的定义构造辅助圆；(2)如图1，若OA=OB =OC，则A、B、C在以O为圆心，OA为半径的圆上.由圆周角定理可得：∠ABC= 1∠AOC,∠ACB=12∠AOB,∠BAC=12∠BOC.2图1【模型2】 90°圆周角模型【模型分析】如图2，在△ABC中，∠C=90°，点C为动点，则点C的轨迹是以AB为直径的⊙O (不包含A、B两点)．注：作出辅助圆是关键，计算时结合求点圆、线圆、最值等方法进行相关计算．图2应用：常用于解决直角三角形中动点的轨迹问题。

【模型3】 定弦定角模型【模型分析】固定的线段只要对应固定的角度，那么这个角的顶点轨迹为圆的一部分．如图①，在⊙O中，若弦AB长度固定，则弦AB所对的圆周角都相等；(注意：弦AB所对的劣弧(AB)上也有圆周角，需要根据题目灵活运用)如图②，若有一固定线段AB及线段AB所对的∠C大小固定，根据圆的知识可知点C不唯一．当∠C<90°时，点C在优弧上运动；当∠C=90°时，点C在半圆上运动，且线段AB是⊙O的直径；当∠C >90°时，点C在劣弧上运动．【模型4】‌四点共圆模型【模型分析】在四边形ABCD中，若∠A+∠C=1800，则A、B、C、D在圆O上，称之为A、B、C、D四点共圆.图3应用：常用于解决四点共圆的问题，如角度相等、线段最值等问题.【题型1】‌定点定长模型......................................................3;【模型2】 90°圆周角模型...................................................6;【题型3】‌定弦定角模型.....................................................11；【题型4】‌四点共圆模型.....................................................15；【题型5】直通中考.........................................................20；【题型6】拓展延伸.........................................................23.第二部分【题型展示与方法点拨】【题型1】 定点定长模型1.(23-24九年级上·福建福州·期末)如图，在等边△ABC中，AB=4，D，E分别是边AB,BC上的动点(不与△ABC的顶点重合)，连接AE,CD相交于点F，连接BF，若∠BDF+∠BEF=180°，则BF的最小值为．【433/433【∠BDF +∠BEF =180°，∠DFE =120°，∠AFC =120°，F 在以O 为圆心OA 的长为半径∠AOC =120°的圆弧上运动OA ,OC ,OB ,OF ，OA =OC =OF ,BF ≥OB -OF ，△AOB ≌△COB ，△AOB 为含30度角的直角三角形进行求解即可．解∵等边△ABC ，∴∠ABC =60°，AB =BC ，∵∠BDF +∠BEF =180°，∴∠DFE +∠ABC =360°-∠BDF +∠BEF =180°，∴∠DFE =120°，∴∠AFC =120°，∴点F 在以O 为圆心OA 的长为半径∠AOC =120°的圆弧上运动OA ,OC ,OB ,OF ，OA =OC =OF ,BF ≥OB -OF ，∵AB =BC ，OB =OB ,OA =OC ，∴△AOB ≌△COB ，∴∠ABO =∠CBO =12∠ABC =30°，∠AOB =∠BOC =12∠AOC =60°，∴∠BAO =90°，∴BO =2AO ，AB =3AO =4，∴AO =433，∴BO =2OA =833，OF =AO =433，∴BF ≤433，BF 的最小值为433；故答案为433．【30度角的直角三角形一点到圆上一点的最值F 的运动轨迹．2.(24-25九年级上·全国·课后作业)如图，P 是边长为1的正方形ABCD 内的一个动点，且满足∠PBC +∠PDC =45°，则CP 的最小值是()A.2-2B.12C.22D.2-1【答案】D【分析】本题考查了正方形的性质、等腰直角三角形的性质、勾股定理、圆周角定理，在凹四边形BCDP中，求出∠BPD=135°，得点P在运动过程中，使得∠BPD=135°，即点P在正方形ABCD内，以A为圆心，AB长为半径的圆弧上，如解图，连接AP，AC，当A、P、C三点共线时，CP取得最小值，最小值为AC-AP，求出AC和AP的长度，即可得到结果，解本题的关键是证明∠BPD是定值，从而得到点P的轨迹．解：∵四边形ABCD是正方形，∴∠BCD=90°，在凹四边形BCDP中，∵∠BCD=90°，∠PBC+∠PDC=45°，∴∠BPC+∠CPD=360°-∠BCD-(∠PBC+∠PDC)=225°，∴∠BPD=360°-(∠BPC+∠CPD)始终为135°，得点P在运动过程中，使得∠BPD=135°，即点P在正方形ABCD内，以A为圆心，AB长为半径的圆弧上，如解图，连接AP，AC，，由解图可得AP+CP≥AC，当A、P、C三点共线时，CP取得最小值，最小值为AC-AP，在Rt△ABC中，∵AB=BC=1，∴AC=AB2+BC2=2，∵AP=AB=1，∴CP最小=AC-AP=2-1，故选：D．3.(24-25九年级上·江苏宿迁)如图，在矩形ABCD中，AB=6，BC=8，点E、F分别是边AB、BC上的动点，且EF=4，点G是EF的中点，AG、CG，则四边形AGCD面积的最小值为()A.30B.32C.35D.38【答案】D【分析】首先连接AC，BG，证明G在以B为圆心，2为半径的圆弧上，过B作BH⊥AC于H，当G在BH 上时，△ACG面积取最小值，此时四边形AGCD面积取最小值，再进一步解答即可．解：连接AC，BG，∵矩形ABCD，∴∠ABC=90°，S矩形=48，∵EF=4，G为EF的中点，∴BG=12EF=2，∴G在以B为圆心，2为半径的圆弧上，过B作BH⊥AC于H，当G在BH上时，△ACG面积取最小值，此时四边形AGCD面积取最小值，四边形AGCD面积=三角形ACG面积+三角形ACD面积，即四边形AGCD面积=三角形ACG面积+24．设圆弧交BH于G ，此时四边形AGCD面积取最小值，由勾股定理得：AC=62+82=10，∵1 2AC⋅BH=12AB⋅BC，∴BH=4.8，∴G H=2.8，即四边形AGCD面积的最小值=12×10×2.8+24=38．故选：D．【点拨】本题考查了勾股定理及矩形中的与动点相关的最值问题，圆的确定，解题的关键是利用直角三角形斜边的直线等于斜边的一半确定出G点的运动轨迹．【题型2】 90°圆周角模型4.(2024·湖南娄底·一模)如图，正方形ABCD的边长为a，点E、F分别在BC、CD上，且BE=CF，AE与BF相交于点G，连接CG，则CG的最小值为．【答案】5-1 a2【分析】本题考查了正方形的性质，圆周角定理，勾股定理，以及全等三角形的判定与性质，熟练掌握90°的圆周角所对的弦是直径是解答本题的关键．通过证明△ABE ≌△BCF SAS ，可证∠AGB =90°，则点G 在以AB 为直径的一段弧上运动，当点G 在OC 与弧的交点处时，CG 最短，然后根据勾股定理求出OC 的长即可求解．解：∵四边形ABCD 是正方形，∴∠ABC =∠BCF =90°，AB =BC =a ，∴在△ABE 和△BCF 中，AB =BC∠ABC =∠BCFBE =CF∴△ABE ≌△BCF SAS ，∴∠BAE =∠CBF ，∵∠ABF +∠CBF =90°，∴∠ABF +∠BAE =90°，∴∠AGB =90°，∴点G 在以AB 为直径的一段弧上运动，设AB 的中点为O ，则当点G 在OC 与弧的交点处时，CG 最短，∵AB =a ，∴OB =OG =a 2，∴OC =a 2 2+a 2=52a ，∴CG=OC -OG =5-1 a 2，故答案为：5-1 a 2．5.(23-24九年级下·山东日照)如图，已知正方形ABCD 的边长为2，点F 是正方形内一点，连接CF ,DF ，且∠ADF =∠DCF ，点E 是AD 边上一动点，连接EB ,EF ，则EB +EF 长度的最小值为()A.13-1B.10-1C.10D.5+1【答案】A【分析】根据正方形的性质得到∠ADC=90°，推出∠DFC=90°，得到点F在以CD为直径的半圆上移动，如图，设CD的中点为O，正方形ABCD关于直线AD对称的正方形ADC B ，则点B 的对应点是B，连接B O交AD于E，交半圆O于F，线段B F的长即为EB+EF的长度最小值，根据勾股定理即可得到结论．解：∵四边形ABCD是正方形，∴∠ADC=90°，∴∠ADF+∠CDF=90°，∵∠ADF=∠DCF，∴∠DCF+∠CDF=90°，∴∠DFC=90°，∴点F在以CD为直径的半圆上移动，如图，设CD的中点为O，正方形ABCD关于直线AD对称的正方形ADC B ，则点B 的对应点是B，连接B O交AD于E，交半圆O于F，线段B F的长即为EB+EF的长度最小值，OF=1，∵∠C =90°,B C =C D =CD=2，∴OC =3，∴OB =B C 2+OC 2=13，∴B F=13-1，∴FD+FE的长度最小值为13-1，故选：A．【点拨】此题考查了正方形的性质，圆周角定理，轴对称的性质，点的运动轨迹，勾股定理，最小值问题，正确理解点的运动轨迹是解题的关键．6.(24-25九年级上·广东深圳·开学考试)如图，E，F是正方形ABCD的边AD上两个动点，满足AE= DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为1，则线段DH长度的最小值是()A.52-1 B.5-12C.52D.5-1【答案】B【分析】由SAS可判定△ABE≌△DCF，由全等三角形的性质得∠ABE=∠DCF，同理可证∠DCG=∠DAG，由角的和差得∠AHB=90°，取AB的中点O，连接OH，H的运动轨迹为以O为圆心，OH=1 2AB=12为半径的半圆，当O、H、D三点共线时，DH最小，即可求解．解：∵四边形ABCD是正方形，∴AB=AD=CD=1，∠BAE=∠CDF=90°，∠ADG=∠CDG，∵∠BAH+∠DAG=90°，在△ABE和△DCF中，AB=CD∠BAE=∠CDFAE=DF，∴△ABE≌△DCF(SAS)，∴∠ABE=∠DCF，在△ADG和△CDG中，AD=CD∠ADG=∠CDGDG=DG，∴△ADG≌△CDG(SAS)，∴∠DCG=∠DAG，∴∠ABE=∠DAG，∴∠ABE+∠BAH=90°，∴∠AHB=90°，如下图，取AB的中点O，连接OH，∴OA=12，∴H的运动轨迹为以O为圆心，OH=12AB=12为半径的半圆，如图，当O、H、D三点共线时，DH最小，∴OD=OA2+AD2=122+12=52，∴DH=OD-OH=52-1 2=5-12；故选：B．【点拨】本题考查了正方形的性质，全等三角形的判定及性质，勾股定理，直角三角形的特征，圆外一点到圆上任一点距离的最值等；能找出动点的运动轨迹及取得最小值的条件，熟练利用勾股定咯求解是解题的关键．【题型3】 定弦定角模型7.(22-23九年级上·江苏南京·阶段练习)如图，CD是△ABC的高，若AB=2，∠ACB=45°，则CD长的最大值为()A.1+2B.4-2C.2D.4【答案】A【分析】在AB上方作以AB为斜边的等腰直角三角形△AOB，根据“定线段对定角度”确定点C在以O为圆心，OA长为半径的圆上运动，当CD经过圆心时CD最长，再计算即可．解：在AB上方作以AB为斜边的等腰直角三角形△AOB，∵∠ACB=45°∴点C在以O为圆心，OA长为半径的圆上运动，∵AB=2，∴OA=OC=2，当CD经过圆心时CD最长∵CD是△ABC的高，∴AD=BD=OD=1AB=12此时CD=OC+OD=2+1，故选：A．【点拨】本题考查几何最值问题，解题的关键是确定点C在以O为圆心，OA长为半径的圆上运动．8.(20-21九年级上·江苏无锡·期末)如图，在平面直角坐标系中，动点A、B分别在x轴上和函数y=x的图象上，AB=4，CB⊥AB，BC=2，则OC的最大值为()A.22+2B.22+4C.25D.25+2【答案】A【分析】根据y=x与x轴的夹角为45°，以AB为斜边作等腰直角三角形，连接AD,CD,OD，则∠DBC= 45°，根据勾股定理求得DB的长，进而证明△DCB是直角三角形，求得DC的长，根据OD+DC≥OC，即可求得OC的最大值解：如图，以AB为斜边作等腰直角三角形，连接AD,CD,OD，∵y=x与x轴的夹角为45°，∴∠AOB=45°=1∠ADB2∴A,O,B在⊙D上，∵AB=4，∠ADB=90°，∴BD=AD=22，∴∠ABD=45°∵BC⊥AB∴∠CBA=90°∴∠CBD=45°∴△BCD中BC=2,BD=22,∠CBD=45°过点C作CE⊥BD于点E，如图则BE=CE=2=DE∴CD=CB=2∵OD+DC≥OC∴当O,D,C三点共线时，OC取得最大值，最大值为OD+DC=DB+DC=22+2故选A【点拨】本题主要考查了勾股定理，同弧所对的圆周角等于圆心角的一半，找到⊙D是解决本题的关键．9.(19-20九年级上·浙江宁波·期末)如图，在等腰Rt△ABC中，∠BAC=90°，BC=2，点P是△ABC内部的一个动点，且满足∠PBC=∠PCA，则线段AP长的最小值为()A.0.5B.2-1C.2-2D.13【答案】C 【分析】先计算出∠PBC +∠PCB =45°，则∠BPC =135°，利用圆周角定理可判断点P 在以BC 为弦的⊙O 上，如图，连接OA 交BC 于P ′，作BC 所对的圆周角∠BQC ，利用圆周角定理计算出∠BOC =90°，从而得到△OBC 为等腰直角三角形，四边形ABOC 为正方形，所以OA =BC =2，OB =2，根据三角形三边关系得到AP ≥OA -OP (当且仅当A 、P 、O 共线时取等号，即P 点在P ′位置)，于是得到AP 的最小值.解：解：∵△ABC 为等腰直角三角形，∴∠ACB =45°，即∠PCB +∠PCA =45°，∵∠PBC =∠PCA ，∴∠PBC +∠PCB =45°，∴∠BPC =135°，∴点P 在以BC 为弦的⊙O 上，如图，连接OA 交BC于P ′，作BC 所对的圆周角∠BQC ，则∠BCQ =180°-∠BPC =45°，∴∠BOC =2∠BQC =90°，∴△OBC 为等腰直角三角形，∴四边形ABOC 为正方形，∴OA =BC =2，∴OB =22BC =2，∵AP ≥OA -OP (当且仅当A 、P 、O 共线时取等号，即P 点在P ′位置)，∴AP 的最小值为2-2．故选：C ．【点拨】本题考查了圆周角定理及等腰直角三角形的性质.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半.推论：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径.【题型4】四点共圆模型10.(22-23九年级上·黑龙江哈尔滨·阶段练习)如图，在四边形ABCD 中，∠ABC =∠D =90°，连接AC ，点F 为边CD 上一点，连接BF 交AC 于点E ，AB =AE ，∠FGC +∠FBG =90°，∠BFG +2∠GFC =180°，若AD =722，BG =4，则CG 的长为．【答案】8【分析】延长BA 与CD 的延长线相交于点H ，证明∠FGC =∠ABF ，∠GFC =∠BFD ，由三角形内角和定理得到∠H=∠ACB，BH=BC，进一步得到∠H=∠DAH=45°，则AD=DH=722，由勾股定理得到AH=AD2+DH2=7，证明点C、G、E、F四点共圆，如图，连接EG，证明CE=CG，设CE=CG=x，则BH=BC=4+x，AE=AB=x-3，AC=2x-3，由勾股定理得AB2+BC2=AC2，即x-32+x+42 =2x-32，解方程即可得到答案．解：延长BA与CD的延长线相交于点H，∵∠FGC+∠FBG=90°，∠FBG+∠ABF=∠ABC=90°∴∠FGC=∠ABF，∵∠BFG+2∠GFC=180°，∠BFG+∠BFD+∠CFG=180°，∴2∠GFC=∠BFD+∠CFG，∴∠GFC=∠BFD，∵∠H+∠ABF+∠BFD=180°=∠ACB+∠FGC+∠GFC，∴∠H=∠ACB，∵∠ABC=90°，∴∠H=∠ACB=45°，BH=BC，∵∠ADH=90°，∴∠H=∠DAH=45°，∴AD=DH=722，∴AH=AD2+DH2=7，∵AB=AE，∴∠ABE=∠AEB，∵∠FGC=∠ABE，∠CEF=∠AEB，∴∠FGC=∠CEF，∴点C、G、E、F四点共圆，如图，连接EG，∴∠GFC=∠CEG，∠BFD=∠CGE，∵∠GFC=∠BFD，∴∠CGE=∠CEG，∴CE=CG，设CE=CG=x，则BH=BC=BG+CG=4+x，∴AE=AB=BH-AH=x+4-7=x-3，∴AC=AE+CE=x-3+x=2x-3，由勾股定理得，AB2+BC2=AC2，∴x-32+x+42=2x-32，解得x=-1(不合题意，舍去)或x=8，∴CG=8，故答案为：8【点拨】此题考查了等腰直角三角形的判定和性质、勾股定理、等腰三角形的判定和性质、四点共圆、圆周角定理、圆内接四边形的性质、解一元二次方程等知识，关键在于等腰直角三角形的判定和性质与证明四点共圆．11.(24-25九年级上·江苏宿迁·阶段练习)如图，等边三角形ABC中，AB=5,P为AB边上一动点，PD⊥BC ,PE ⊥AC ，垂足分别为D ,E 则DE 的最小值为．【答案】154【分析】如图，连接PC ，取CP 的中点O ，连接OE ，OD ，过点O 作OH ⊥DE 于H ，首先证明△ODE 是顶角为120°的等腰三角形，当OE 的值最小时，DE 的值最小，即可求出PC 的最小值．解：如图，连接PC ，取CP 的中点O ，连接OE ，OD ，过点O 作OH ⊥DE 于H ，∵△ABC 是等边三角形，∴∠ACB =60°，AB =BC =AC =5，∵PD ⊥BC ，PE ⊥AC ，∴∠PEC =∠PDC =90°，∵OP =OC ，∴OE =OP =OC =OD ，∴C 、D 、P 、E 四点共圆，∴∠EOD =2∠ECD =120°，∴当OE 的值最小时，DE 的值最小，根据垂线段最短可得，当CP ⊥AB 时，PC =532，此时OE 最小，OE =534，∵OE =OD ，OH ⊥DE ，∴DH =EH ，∠DOH =∠EOH =60°，∴∠OEH =30°，∴OH =12OE =538，∴DH =EH =OE 2-OH 2=158，∴DE =2DH =154，∴DE 的值最小为154，故答案为：154．【点拨】本题考查了四点共圆、垂线段最短、圆周角定理、含30°角的直角三角形的性质、等腰直角三角形的判定与性质等知识；正确判断当CP ⊥AB 时OE 最小是解题的关键．12.(23-24九年级下·江苏南京·阶段练习)如图，在△ABC 中，∠ACB =90°,AC =BC =2，点P 是射线AB 上一动点，∠CPD =90°，且PC =PD ，连接AD 、CD ，则AD +CD 的最小值是．【答案】25【分析】取AC中点H，连接DH交AB于点G，连接BD,PH，当DH⊥AC时，DH有最小值，此时易得△ACD是等腰三角形，推出AD=CD，即AD,CD有最小值，则AD+CD有最小值，此时根据∠AHD=∠CHD=∠ACB=90°，推出DH∥BC，设CD中点为O，根据∠CHD=∠CPD=90°，易得点C,H,P,D在以点O为圆心CD为直径的圆上，易得∠CHP+∠PDC=180°，由∠ABC=45°，易得此时点B在圆O上，进而推出∠CBD+∠CPD=180°，则∠CBD=90°，得到四边形BCHD是矩形，即HD=BC=2，利用勾股定理即可计算出CD的最小值，进而得出结果．解：取AC中点H，连接DH交AB于点G，连接BD,PH，当DH⊥AC时，DH有最小值，∵点H是AC中点，DH⊥AC，∴△ACD是等腰三角形，∴AD=CD，∵AH,CH是定值，DH有最小值时，即AD,CD有最小值，则AD+CD有最小值，∵∠AHD=∠CHD=∠ACB=90°，∴DH∥BC，设CD中点为O，∵∠CHD=∠CPD=90°，∴点C,H,P,D在以点O为圆心CD为直径的圆上，∴∠CHP+∠PDC=180°，∵∠ABC=45°，∴此时点B在圆O上，∴∠CBD+∠CPD=180°，∴∠CBD=90°，∵DH∥BC，∴四边形BCHD是矩形，∴HD=BC=2，∵HC=1AC=1，2在Rt△CHD中，∴CD=CH2+HD2=5，∴AD+CD的最小值为2CD=25，故答案为：25．【点拨】本题考查勾股定理求最短距离，圆周角定理，四点共圆，等腰三角形的判定与性质，矩形的判定与性质，正确作出辅助线，证明四点共圆是解题的关键．第三部分【中考链接与拓展延伸】1、直通中考1.(2023·山东泰安·中考真题)如图，在平面直角坐标系中，Rt △AOB 的一条直角边OB 在x 轴上，点A 的坐标为(-6，4)；Rt △COD 中，∠COD =90°，OD =43，∠D =30°，连接BC ，点M 是BC 中点，连接AM ．将Rt △COD 以点O 为旋转中心按顺时针方向旋转，在旋转过程中，线段AM 的最小值是()A.3B.62-4C.213-2D.2【答案】A【分析】如图所示，延长BA 到E ，使得AE =AB ，连接OE ，CE ，根据点A 的坐标为(-6，4)得到BE =8，再证明AM 是△BCE 的中位线，得到AM =12CE ；解Rt △COD 得到OC =4，进一步求出点C 在以O 为圆心，半径为4的圆上运动，则当点M 在线段OE 上时，CE 有最小值，即此时AM 有最小值，据此求出CE 的最小值，即可得到答案．解：如图所示，延长BA 到E ，使得AE =AB ，连接OE ，CE ，∵Rt △AOB 的一条直角边OB 在x 轴上，点A 的坐标为(-6，4)，∴AB =4，OB =6，∴AE =AB =4，∴BE =8，∵点M 为BC 中点，点A 为BE 中点，∴AM 是△BCE 的中位线，∴AM =12CE ；在Rt △COD 中，∠COD =90°，OD =43，∠D =30°，∴OC =33OD =4，∵将Rt △COD 以点O 为旋转中心按顺时针方向旋转，∴点C 在以O 为圆心，半径为4的圆上运动，∴当点M 在线段OE 上时，CE 有最小值，即此时AM 有最小值，∵OE =BE 2+OB 2=10，∴CE 的最小值为10-4=6，∴AM 的最小值为3，故选A ．【点拨】本题主要考查了一点到圆上一点的最值问题，勾股定理，三角形中位线定理，坐标与图形，含30度角的直角三角形的性质等等，正确作出辅助线是解题的关键．2.(2022·广西柳州·中考真题)如图，在正方形ABCD中，AB=4，G是BC的中点，点E是正方形内一个动点，且EG=2，连接DE，将线段DE绕点D逆时针旋转90°得到线段DF，连接CF，则线段CF长的最小值为．【答案】25-2【分析】如图，由EG=2，确定E在以G为圆心，半径为2的圆上运动，连接AE，再证明△ADE≌△CDF (SAS)，可得AE=CF，可得当A，E，G三点共线时，AE最短，则CF最短，再利用勾股定理可得答案．解：如图，由EG=2，可得E在以G为圆心，半径为2的圆上运动，连接AE，∵正方形ABCD，∴AD=CD,∠ADC=90°，∴∠ADC=∠EDF=90°，∴∠ADE=∠CDF，∵DE=DF，∴△ADE≌△CDF(SAS)，∴AE=CF，∴当A，E，G三点共线时，AE最短，则CF最短，∵G位BC中点，BC=AB=4，∴BG=2，此时AG=BG2+AB2=22+42=25，此时AE=25-2，所以CF的最小值为：25-2.故答案为：25-2【点拨】本题考查的是正方形的性质，圆的基本性质，勾股定理的应用，二次根式的化简，熟练的利用圆的基本性质求解线段的最小值是解本题的关键．2、拓展延伸3.(2022·辽宁抚顺·中考真题)如图，正方形ABCD的边长为10，点G是边CD的中点，点E是边AD上一动点，连接BE，将△ABE沿BE翻折得到△FBE，连接GF．当GF最小时，AE的长是．【答案】55-5【分析】根据动点最值问题的求解步骤：①分析所求线段端点(谁动谁定)；②动点轨迹；③最值模型(比如将军饮马模型)；④定线段；⑤求线段长(勾股定理、相似或三角函数)，结合题意求解即可得到结论．解：①分析所求线段GF端点：G是定点、F是动点；②动点F的轨迹：正方形ABCD的边长为10，点E是边AD上一动点，连接BE，将△ABE沿BE翻折得到△FBE，连接GF，则BF=BA=10，因此动点轨迹是以B为圆心，BA=10为半径的圆周上，如图所示：③最值模型为点圆模型；④GF最小值对应的线段为GB-10；⑤求线段长，连接GB，如图所示：在RtΔBCG中，∠C=90°，正方形ABCD的边长为10，点G是边CD的中点，则CG=5,BC=10，根据勾股定理可得BG=CG2+BC2=52+102=55，当G、F、B三点共线时，GF最小为55-10，接下来，求AE的长：连接EG，如图所示=SΔEDG+SΔBCG+根据翻折可知EF=EA,∠EFB=∠EAB=90°，设AE=x，则根据等面积法可知S正方形SΔBAE+SΔBEG，即100=12DE⋅DG+12BC⋅CG+12AB⋅AE+12BG⋅EF=1 2510-x+5×10+10x+55x整理得5+1x=20，解得x=AE=205+1=205-15+15-1=55-5，故答案为：55-5．【点拨】本题考查动点最值下求线段长，涉及到动点最值问题的求解方法步骤，熟练掌握动点最值问题的相关模型是解决问题的关键．4.(2024·内蒙古兴安盟·二模)如图，在正方形ABCD中，点M，N分别为AB，BC上的动点，且AM= BN，DM，AN交于点E，点F为AB的中点，点P为BC上一个动点，连接PE，PF，若AB=4，则PE +PF的最小值为．【答案】210-2【分析】证明△DAM≌△ABN SAS，则∠ADM=∠BAN，∠AED=90°，如图，取AD的中点O，则E在以O为圆心，AD为直径的圆上运动，作F关于BC对称的点F ，连接PF ，连接OF 交⊙O于E ，则PF = PF，由PE+PF=PE+PF ，可知当O、E 、P、F 四点共线时，PE+PF最小为E F ，由勾股定理得，OF =AF 2+OA2=210，根据E F =OF -OE ，求解作答即可．解：∵正方形ABCD，∴AD=AB，∠DAM=∠ABN=90°，又∵AM=BN，∴△DAM≌△ABN SAS，∴∠ADM=∠BAN，∴∠ADM+∠DAE=∠BAN+∠DAE=90°，∴∠AED=90°，如图，取AD的中点O，则E在以O为圆心，AD为直径的圆上运动，作F关于BC对称的点F ，连接PF ，连接OF 交⊙O于E ，∴PF =PF，∴PE+PF=PE+PF ，∴当O、E 、P、F 四点共线时，PE+PF最小为E F ，由勾股定理得，OF =AF 2+OA2=62+22=210，∴E F =OF -OE =210-2，故答案为：210-2．【点拨】本题考查了正方形的性质，全等三角形的判定与性质，90°圆周角所对的弦为直径，轴对称的性质，勾股定理等知识．熟练掌握正方形的性质，全等三角形的判定与性质，90°圆周角所对的弦为直径，轴对称的性质，勾股定理是解题的关键．。

高考数学二轮复习考点知识与题型专题讲解第48讲 隐圆(阿波罗尼斯圆)问题隐圆问题近几年在高考题和各地模拟题中都出现过，难度为中高档，在题设中没有明确给出圆的相关信息，而是隐含在题目中，要通过分析、转化、发现圆(或圆的方程)，从而最终利用圆的知识来求解，我们称这类问题为“隐圆问题”．考点一 利用圆的定义、方程确定隐形圆例1 (1)(2022·滁州模拟)已知A ，B 为圆C ：x 2＋y 2－2x －4y ＋3＝0上的两个动点，P 为弦AB 的中点，若∠ACB ＝90°，则点P 的轨迹方程为( ) A ．(x －1)2＋(y －2)2＝14B ．(x －1)2＋(y －2)2＝1C ．(x ＋1)2＋(y ＋2)2＝14D ．(x ＋1)2＋(y ＋2)2＝1 答案 B解析 圆C 即(x －1)2＋(y －2)2＝2，半径r ＝2，因为CA ⊥CB ， 所以|AB |＝2r ＝2， 又P 是AB 的中点，所以|CP |＝12|AB |＝1，所以点P 的轨迹方程为(x －1)2＋(y －2)2＝1.(2)(2022·茂名模拟)已知向量a ，b 满足|a |＝1，|b |＝2，a ·b ＝0，若向量c 满足|a ＋b －2c |＝1，则|c |的取值范围是( ) A ．[1，5－1] B.⎣⎢⎡⎦⎥⎤3－12，3＋12C.⎣⎢⎡⎦⎥⎤5－12，5＋12 D.⎣⎢⎡⎦⎥⎤5＋12，52答案 C解析 |a |＝1，|b |＝2，a ·b ＝0，以a 为y 轴，b 为x 轴，建立平面直角坐标系， 设OA →＝a ＝(0,1)，OB →＝b ＝(2,0)， OC →＝c ＝(x ，y )，所以a ＋b －2c ＝(2－2x ，1－2y )， 由|a ＋b －2c |＝1，可得(2－2x )2＋(1－2y )2＝1， 化简可得(x －1)2＋⎝⎛⎭⎫y －122＝⎝⎛⎭⎫122， 所以点C 的轨迹是以⎝⎛⎭⎫1，12为圆心，以r ＝12为半径的圆，原点(0,0)到⎝⎛⎭⎫1，12的距离为d ＝12＋⎝⎛⎭⎫122＝52， 所以|c |＝x 2＋y 2的取值范围是[d －r ，d ＋r ]，即⎣⎢⎡⎦⎥⎤5－12，5＋12.规律方法 对于动点的轨迹问题，一是利用曲线(圆、椭圆、双曲线、抛物线等)的定义识别动点的轨迹，二是利用直接法求出方程，通过方程识别轨迹．跟踪演练1 (2022·平顶山模拟)已知M ，N 为圆C ：x 2＋y 2－2x －4y ＝0上两点，且|MN |＝4，点P 在直线l ：x －y ＋3＝0上，则|PM →＋PN →|的最小值为( )A ．22－2B ．2 2C ．22＋2D ．22－ 5 答案 A解析 设线段MN 的中点为D ，圆C ：x 2＋y 2－2x －4y ＝0的圆心为C (1,2)，半径为 5.则圆心C 到直线MN 的距离为(5)2－⎝⎛⎭⎫422＝1，所以|CD |＝1，故点D 的轨迹是以C 为圆心，半径为1的圆，设点D 的轨迹为圆D ，圆D 上的点到直线l 的最短距离为t ＝|1－2＋3|2－1＝2－1.所以|PM →＋PN →|＝|2PD →|＝2|PD →|≥2t ＝22－2.考点二 由圆周角的性质确定隐形圆例2 (1)已知点P (2，t )，Q (2，－t )(t >0)，若圆C ：(x ＋2)2＋(y －3)2＝1上存在点M ，使得∠PMQ ＝90°，则实数t 的取值范围是( ) A ．[4,6] B ．(4,6)C ．(0,4]∪[6，＋∞)D ．(0,4)∪(6，＋∞) 答案 A解析 由题意知，点P (2，t )，Q (2，－t )(t >0)， 可得以PQ 为直径的圆的方程为(x －2)2＋y 2＝t 2， 则圆心C 1(2,0)，半径R ＝t ， 又由圆C ：(x ＋2)2＋(y －3)2＝1， 可得圆心C (－2,3)，半径r ＝1，两圆的圆心距为|CC 1|＝(2＋2)2＋(0－3)2＝5，要使得圆C ：(x ＋2)2＋(y －3)2＝1上存在点M ，使得∠PMQ ＝90°，即两圆存在公共点，则满足⎩⎪⎨⎪⎧R ＋r ≥5，R －r ≤5，即⎩⎪⎨⎪⎧t ＋1≥5，t －1≤5，解得4≤t ≤6，所以实数t 的取值范围是[4,6]．(2)(2022·长沙雅礼中学质检)已知直线l ：x －y ＋4＝0上动点P ，过P 点作圆x 2＋y 2＝4的两条切线，切点分别为C ，D ，记M 是CD 的中点，则直线CD 过定点________，点M 的轨迹方程为______________________________． 答案 (－1,1) ⎝⎛⎭⎫x ＋122＋⎝⎛⎭⎫y －122＝12 解析 如图，连接PO ，CO ，DO ，因为PD ⊥DO ，PC ⊥CO ，所以P ，D ，O ，C 在以PO 为直径的圆上， 设P (x 0，x 0＋4)，则以OP 为直径的圆的方程为⎝⎛⎭⎫x －x 022＋⎝⎛⎭⎫y －x 0＋422＝x 20＋(x 0＋4)24， 化简得x 2－x 0x －(x 0＋4)y ＋y 2＝0， 与x 2＋y 2＝4联立，可得CD 所在直线的方程为x 0x ＋(x 0＋4)y ＝4⇒x 0(x ＋y )＝4(1－y )⇒⎩⎪⎨⎪⎧ 1－y ＝0，x ＋y ＝0⇒⎩⎪⎨⎪⎧y ＝1，x ＝－1，直线CD 过定点Q (－1,1)，又OM ⊥CD ，所以OM ⊥MQ ，所以点M 在以OQ 为直径的圆上， 所以点M 的轨迹为⎝⎛⎭⎫x ＋122＋⎝⎛⎭⎫y －122＝12. 规律方法 利用圆的性质，圆周角为直角，即可得到：若P A ⊥PB 或∠APB ＝90°，则点P 的轨迹是以AB 为直径的圆．注意轨迹中要删除不满足条件的点．跟踪演练2 (2022·北京海淀区模拟)在平面直角坐标系中，直线y ＝kx ＋m (k ≠0)与x 轴和y 轴分别交于A ，B 两点，|AB |＝22，若CA ⊥CB ，则当k ，m 变化时，点C 到点(1,1)的距离的最大值为( ) A ．4 2 B ．3 2 C ．2 2 D. 2 答案 B解析 由y ＝kx ＋m (k ≠0)得A ⎝⎛⎭⎫－mk ，0，B (0，m )， 因为CA ⊥CB ，所以点C 的轨迹是以AB 为直径的圆，其方程为⎝⎛⎭⎫x ＋m 2k 2＋⎝⎛⎭⎫y －m 22＝m 24k 2＋m24， 设该动圆的圆心为(x ′，y ′)，则x ′＝－m 2k ，y ′＝m2，整理得k ＝－y ′x ′，m ＝2y ′，代入到⎝⎛⎭⎫－mk 2＋m 2＝8中，得x ′2＋y ′2＝2， 即点C 轨迹的圆心在圆x ′2＋y ′2＝2上，故点(1,1)与该圆上的点(－1，－1)的连线的距离加上圆的半径即为点C 到点(1,1)的距离的最大值，最大值为[1－(－1)]2＋[1－(－1)]2＋2＝3 2.考点三 阿波罗尼斯圆例3(多选)古希腊著名数学家阿波罗尼斯发现“若A ，B 为平面上相异的两点，则所有满足：|P A ||PB |＝λ(λ>0，且λ≠1)的点P 的轨迹是圆，后来人们称这个圆为阿波罗尼斯圆．在平面直角坐标系中，A (－2,0)，B (4,0)，若λ＝12，则下列关于动点P 的结论正确的是( )A ．点P 的轨迹方程为x 2＋y 2＋8x ＝0B ．△APB 面积的最大值为6C ．在x 轴上必存在异于A ，B 的两定点M ，N ，使得|PM ||PN |＝12D ．若点Q (－3,1)，则2|P A |＋|PQ |的最小值为5 2 答案 ACD解析 对于选项A ，设P (x ，y )，因为P 满足|P A ||PB |＝12，所以(x ＋2)2＋y 2(x －4)2＋y 2＝12，化简得x 2＋y 2＋8x ＝0，故A 正确； 对于选项B ，由选项A 可知， 点P 的轨迹方程为x 2＋y 2＋8x ＝0，即(x ＋4)2＋y 2＝16，所以点P 的轨迹是以(－4,0)为圆心，4为半径的圆， 又|AB |＝6，且点A ，B 在直径所在直线上，故当点P 到圆的直径所在直线的距离最大时，△P AB 的面积取得最大值， 因为圆上的点到直径的最大距离为半径，即△P AB 的高的最大值为4， 所以△P AB 面积的最大值为12×6×4＝12，故B 错误；对于选项C ，假设在x 轴上存在异于A ，B 的两定点M ，N ，使得|PM ||PN |＝12，设M (m ，0)，N (n ，0)，故(x －m )2＋y 2(x －n )2＋y 2＝12，即(x －n )2＋y 2＝2(x －m )2＋y 2， 化简可得x 2＋y 2－8m －2n 3x ＋4m 2－n 23＝0,又点P 的轨迹方程为x 2＋y 2＋8x ＝0， 可得⎩⎨⎧－8m －2n3＝8，4m 2－n23＝0，解得⎩⎪⎨⎪⎧ m ＝－6，n ＝－12或⎩⎪⎨⎪⎧m ＝－2，n ＝4(舍去)， 故存在异于A ，B 的两定点M (－6,0)，N (－12,0)， 使得|PM ||PN |＝12，故C 正确；对于选项D ，因为|P A ||PB |＝12，所以2|P A |＝|PB |，所以2|P A |＋|PQ |＝|PB |＋|PQ |，又点P 在圆x 2＋8x ＋y 2＝0上，如图所示，所以当P ，Q ，B 三点共线时2|P A |＋|PQ |取得最小值，此时(2|P A |＋|PQ |)min ＝|BQ | ＝[4－(－3)]2＋(0－1)2＝52，故D 正确．规律方法 “阿波罗尼斯圆”的定义：平面内到两个定点A (－a ，0)，B (a ，0)(a >0)的距离之比为正数λ(λ≠1)的点的轨迹是以C ⎝ ⎛⎭⎪⎫λ2＋1λ2－1a ，0为圆心，⎪⎪⎪⎪2aλλ2－1为半径的圆，即为阿波罗尼斯圆．跟踪演练3 若平面内两定点A ，B 间的距离为2，动点P 满足|P A ||PB |＝3，则|P A |2＋|PB |2的最大值为( )A ．16＋83B ．8＋4 3C ．7＋43D ．3＋ 3 答案 A解析 由题意，设A (－1,0)，B (1,0)，P (x ，y )， 因为|P A ||PB |＝3，所以(x ＋1)2＋y 2(x －1)2＋y 2＝3，即(x －2)2＋y 2＝3，所以点P 的轨迹是以(2,0)为圆心，半径为3的圆，因为|P A |2＋|PB |2＝(x ＋1)2＋y 2＋(x －1)2＋y 2＝2(x 2＋y 2＋1)，其中x 2＋y 2可看作圆(x －2)2＋y 2＝3上的点(x ，y )到原点(0,0)的距离的平方， 所以(x 2＋y 2)max ＝(2＋3)2＝7＋43，所以[2(x 2＋y 2＋1)]max ＝16＋83， 即|P A |2＋|PB |2的最大值为16＋8 3.专题强化练1．已知圆O ：x 2＋y 2＝1，圆M ：(x －a )2＋(y －2)2＝2.若圆M 上存在点P ，过点P 作圆O 的两条切线，切点为A ，B ，使得P A ⊥PB ，则实数a 的取值范围为( ) A ．[0，2] B ．[－52，1] C ．[－2，2] D ．[－2,2] 答案 D解析 由题意可知四边形P AOB 为正方形， |OP |＝2，∴点P 在以O 为圆心，以2为半径的圆上，其方程为x 2＋y 2＝2， 若圆M 上存在这样的点P ，则圆M 与x 2＋y 2＝2有公共点， 则有2－2≤a 2＋4≤2＋2， 解得－2≤a ≤2.2．已知点A (－5，－5)在动直线mx ＋ny －m －3n ＝0上的射影为点B ，若点C (5，－1)，那么|BC |的最大值为( )A ．16B ．14C ．12D ．10 答案 C解析 由动直线方程化为m (x －1)＋n (y －3)＝0，可知其恒过定点Q (1,3)． 又∵点A (－5，－5)在动直线mx ＋ny －m －3n ＝0上的射影为点B ， ∴∠ABQ ＝90°，则点B 的轨迹是以AQ 为直径的圆， ∴圆心为AQ 的中点M (－2，－1)， 圆的半径r ＝12|AQ |＝5.又|MC |＝(5＋2)2＋(－1＋1)2＝7>r ＝5，∴点C (5，－1)在圆M 外，故|BC |的最大值为r ＋|MC |＝7＋5＝12.3．(2022·武汉模拟)已知O 为坐标原点，点A (cos α，sin α)，B ⎝⎛⎭⎫cos ⎝⎛⎭⎫α＋π3，sin ⎝⎛⎭⎫α＋π3，以OA ，OB 为邻边作平行四边形AOBP ，Q (－2,0)，则∠PQO 的最大值为( ) A.π6 B.π4 C.π3 D.π2 答案 C解析 已知圆O ：x 2＋y 2＝1，A ，B 是圆O 上两动点，且∠AOB ＝π3，所以△AOB 为等边三角形， 又|AB |＝|OA |＝1， 取AB 的中点M ，则|OM |＝32， 所以|OP |＝3，所以点P 的轨迹方程为x 2＋y 2＝3， 当PQ 与x 2＋y 2＝3相切时，∠PQO 最大， 此时sin ∠PQO ＝32， 则∠PQO ＝π3.4．已知△ABC 是等边三角形，E ，F 分别是AB 和AC 的中点，P 是△ABC 边上一动点，则满足PE →·PF →＝BE →·CF →的点P 的个数为( ) A ．1 B ．2 C ．3 D ．4 答案 D解析 以BC 的中点O 为坐标原点，BC ，OA 所在直线为x 轴、y 轴，建立如图所示的平面直角坐标系．设△ABC 的边长为4，则B (－2,0)，C (2,0)，A (0,23)，E (－1，3)， F (1，3)，BE →＝(1，3)，CF →＝(－1，3)， 设P (x ，y )，则PE →＝(－1－x ，3－y )， PF →＝(1－x ，3－y )， 由PE →·PF →＝BE →·CF →得，(－1－x ，3－y )·(1－x ，3－y ) ＝(1，3)·(－1，3)， 所以x 2＋(y －3)2＝3，即点P 的轨迹是以(0，3)为圆心，3为半径的圆，也就是以AO 为直径的圆，易知该圆与△ABC 的三边有4个公共点．5．(多选)已知AB 为圆O ：x 2＋y 2＝49的弦，且点M (4,3)为AB 的中点，点C 为平面内一动点，若AC 2＋BC 2＝66，则( ) A ．点C 构成的图象是一条直线 B ．点C 构成的图象是一个圆 C ．OC 的最小值为2 D ．OC 的最小值为3 答案 BC解析 ∵点M (4,3)为AB 的中点，∴OM ⊥AB ，|OM |＝42＋32＝5，∴|AM |＝|BM |＝49－52＝26，∵AC 2＋BC 2＝66，∴AC →2＋BC →2＝66，则(AM →＋MC →)2＋(BM →＋MC →)2＝66，即AM →2＋2AM →·MC →＋MC →2＋BM →2＋2BM →·MC →＋MC →2＝66，∵AM →＝－BM →，则可得2AM →2＋2MC →2＝66，可解得|MC |＝3，∴点C 构成的图象是以M 为圆心，3为半径的圆，故A 错误，B 正确；∴可得OC 的最小值为|OM |－3＝5－3＝2，故C 正确，D 错误．6．(多选)(2022·福州模拟)已知A (－3,0)，B (3,0)，动点C 满足|CA |＝2|CB |，记C 的轨迹为Γ.过A 的直线与Γ交于P ，Q 两点，直线BP 与Γ的另一个交点为M ，则( )A ．Q ，M 关于x 轴对称B ．△P AB 的面积的最大值为6 3C ．当∠PMQ ＝45°时，|PQ |＝4 2D ．直线AC 的斜率的范围为[－3，3]答案 AC解析 设C (x ，y )，由|CA |＝2|CB |得，(x ＋3)2＋y 2＝2(x －3)2＋y 2，整理得Γ的方程为(x －5)2＋y 2＝16，其轨迹是以D (5,0)为圆心，半径r ＝4的圆．由图可知，由于AB ＝6，所以当DP 垂直于x 轴时，△P AB 的面积有最大值，所以(S △P AB )max ＝12|AB |·r ＝12×6×4＝12， 选项B 错误；因为|P A |＝2|PB |，|MA |＝2|MB |，所以|P A ||MA |＝|PB ||MB |，所以∠P AB ＝∠MAB ， 又C 的轨迹Γ关于x 轴对称，所以Q ，M 关于x 轴对称，选项A 正确；当∠PMQ ＝45°时，∠PDQ ＝45°×2＝90°，则△DPQ 为等腰直角三角形，|PQ |＝2r ＝42，选项C 正确；当直线AC 与圆D 相切时，CD ⊥AC ，此时|AD |＝8＝2r＝2|CD |，所以sin ∠DAC ＝12， 所以切线AC 的倾斜角为30°和150°，由图可知，直线AC 的斜率的取值范围为⎣⎡⎦⎤－33，33，选项D 错误．7．已知等边△ABC 的边长为2，点P 在线段AC 上，若满足P A →·PB →－2λ＋1＝0的点P 恰有两个，则实数λ的取值范围是______________．答案⎝⎛⎦⎤38，12解析 如图，以AB 的中点O 为坐标原点，AB ，OC 所在直线为x 轴、y 轴，建立平面直角坐标系，则A (－1,0)，B (1,0)，设P (x ，y )．则P A →·PB →－2λ＋1＝0，即为(－1－x )(1－x )＋y 2－2λ＋1＝0，化简得x 2＋y 2＝2λ(λ>0)，故所有满足P A →·PB →－2λ＋1＝0的点P 在以O 为圆心，2λ为半径的圆上．过点O 作OM ⊥AC ，垂足为点M ，由题意知，线段AC 与圆x 2＋y 2＝2λ有两个交点，所以|OM |<2λ≤|OA |， 即32<2λ≤1，解得38<λ≤12. 8．已知⊙M ：x 2＋y 2－2x －2y －2＝0，直线l ：2x ＋y ＋2＝0，P 为l 上的动点，过点P 作⊙M 的切线P A ，PB ，切点为A ，B ，当|PM |·|AB |取得最小值时，直线AB 的方程为________________． 答案 2x ＋y ＋1＝0解析 ⊙M ：(x －1)2＋(y －1)2＝4，①则圆心M (1,1)，⊙M 的半径为2.如图，由题意可知PM ⊥AB ，∴S 四边形P AMB ＝12|PM |·|AB | ＝|P A |·|AM |＝2|P A |，∴|PM |·|AB |＝4|P A |＝4|PM |2－4.当|PM |·|AB |最小时，|PM |最小，此时PM ⊥l .故直线PM 的方程为y －1＝12(x －1)， 即x －2y ＋1＝0.由⎩⎪⎨⎪⎧ x －2y ＋1＝0，2x ＋y ＋2＝0，得⎩⎪⎨⎪⎧x ＝－1，y ＝0， ∴P (－1,0)．依题意知P ，A ，M ，B 四点共圆，且PM 为圆的直径，∴该圆方程为x 2＋⎝⎛⎭⎫y －122＝54，② 由①－②整理得2x ＋y ＋1＝0，即直线AB 的方程为2x ＋y ＋1＝0.。

中考数学复习隐形圆问题大全一定点+定长1.依据：到定点的距离等于定长的点的集合是以定点为圆心定长为半径的圆。

2.应用：（1）如图，四边形ABCD中，AB=AC=AD=2，BC=1，AB∥CD，求BD的长。

简析：因AB=AC=AD=2，知B、C、D在以A为圆2为半径的圆上，由AB∥CD 得DE=BC=1，易求BD=15。

（2）如图，在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC 边上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是.简析：E为定点，EB′为定长，B′点路径为以E为圆心EB′为半径的圆，作穿心线DE得最小值为210。

（3）ΔABC中，AB=4，AC=2，以BC为边在ΔABC外作正方形BCDE，BD、CE 交于点O，则线段AO的最大值为.简析：先确定A、B点的位置，因AC=2，所以C点在以A为圆心，2为半径的圆上；因点O是点C以点B为中心顺时针旋转45度并1：√2缩小而得，所以把圆A旋转45度再1：2缩小即得O点路径。

如下图，转化为求定点A到定圆F的最长路径，即AF+FO=32。

二定线+定角1.依据：与一条定线的两端夹角一定的动点路径是以定线为弦，定角为圆周角的弧。

2.应用：（1）矩形ABCD中，AB=10，AD=4，点P是CD上的动点，当∠APB=90°时求DP的长.简析：AB为定线，∠APB为定角（90°），P点路径为以AB为弦（直径）的弧，如下图，易得DP为2或8。

（2）如图，∠XOY = 45°，等边三角形ABC的两个顶点A、B分别在OX、OY上移动，AB = 2，那么OC的最大值为.简析：AB为定线，∠XOY为定角，O点路径为以AB为弦所含圆周角为45°的弧，如下图，转化为求定点C到定圆M的最长路径，即CM+MO=3+1+2。

（3）已知A（2，0），B（4，0）是x轴上的两点，点C是y轴上的动点，当∠ACB最大时，则点C的坐标为_____．简析：作ΔABC的处接圆M，当∠ACB最大时，圆心角∠AMB最大，当圆M 半径最小时∠AMB最大，即当圆M与y轴相切时∠ACB最大。

2.应用：（1）如图，四边形ABCD二定线+定角1.依据：与一条定线的两端夹角一定的动点路径是以定线为弦，定角为圆周角的弧。

2.应用：（1）矩形ABCD中，AB=10，AD=4，点P是CD上的动点，当∠APB=90°时求DP的长.简析：AB为定线，∠APB为定角（90°），P点路径为以AB为弦（直径）的弧，如下图，易得DP为2或8。

（2）如图，∠XOY = 45°，等边三角形ABC的两个顶点A、B分别在OX、OY上移动，AB = 2，那么OC的最大值为.简析：作ΔABC的处接圆（4）如图,在平面直角坐标系中三三点定圆1.依据：不在同一直线上的三点确定一个圆。

2.应用：ΔABC中，∠A＝45°，AD⊥BC于D，BD=4，CD=6，求AD的长。

简析：作ΔABC的外接圆，如下图，易得AD=7+5=12。

四四点共圆1.依据：对角互补的四边形四个顶点共圆（或一边所对两个角相等）。

2.应用：如图，在矩形ABCD中， AB=6，AD=8，P、E分别是线段AC、BC上的点，四边形PEFD为矩形，若AP=2，求CF的长。

简析：因∠PEF=∠PDF=∠DCE=90°，知D、F、C、E、P共圆，如下图，由∠1=∠2、∠4=∠5，易得ΔAPD∼ΔDCF，CF：AP＝CD：AD，得CF＝1.5。

五旋转生圆1.如图，圆O的半径为5，A、B是圆上任意两点，且AB=6，以为AB边作正方形ABCD（点D、P在直线两侧），若AB边绕点P旋转一周，则CD边扫过的面积为_____ 。

简析：CD旋转一周扫过的图形可以用两点确定，一是最远点距离为PC，二是最近点距离为P到直线CD的垂线段，从而确定两个圆，CD即为两圆之间的圆环，如下图。

2.如图，在ΔABC中，∠BAC=90°，AB=5cm，AC=2cm，将ΔABC绕顶点C按顺时针方向旋转至ΔA'B'C的位置，则线段AB扫过区域的面积为_____。

隐形圆（引圆）最值问题：我们首先要知道圆上一动点到平面内一定点距离的何时取得最小值和最大值；1》当定点在圆外时，如图所示动点P是在圆o上运动，定点C在圆o外，连接CO并延长，连接OP；我们令OC=d，OP=r；（1）当P，O，C三点不共线时P，O，C三点围成三角形，OC-OP<PC<OC+OP；即d-r<PC<d+r;（2）当P，O，C三点共线时，①P在P’处时，OC-OP=PC,即d-r=PC；②P在P1处时，OC+OP=PC,即d+r=PC；综上可得d-r≤PC≤d+r，PC min=d-r，PC max=d+r.2》当定点在圆内时（不与圆心重合）如图所示：动点P是在圆o上运动，定点C在圆o内，连接CO并双向延长，连接OP；我们令OC=d，OP=r；（1）当P，O，C三点不共线时P，O，C三点围成三角形，OP-OC<PC<OC+OP；即r-d<PC<d+r;（2）当P，O，C三点共线时，①P在P’处时，OP-OC=PC,即r-d=PC；②P在P1处时，OC+OP=PC,即d+r=PC；综上可得r-d≤PC≤d+r，PC min=r-d，PC max=d+r.1.折叠引圆：如图所示在矩形ABCD中，AB=4，AD=6.点E为AB边中点，F为边BC上一动点，以EF为折痕将三角形BEF折叠点B落在B’处，求线段DB’最小值.解析：由题中条件可知折痕EF 满足一定一动的特点，所以满足折叠引圆，根据折叠的性质我们可得到EB=EB ’=21AB=2,根据圆的定义可知，动点B ’是以E 为圆心，2为半径的圆上运动，而B ’的运动又与动点F 有关，我们如果我们将F 看成是从点B →C 的运动可得到B ’的轨迹，如下图所示，B ’的运动并不是完整的圆，而是一部分圆弧。

根据圆上一动点到圆外一定点的最小值分析可知，B ’D 取得最小值时，B ’，D ，E 三点共线，B ’在G 处；所以B ’D min =DE-EG,在直角三角形ADE 中，DE=，因为EG=EB=2，所以B ’D min =-2例1. 如图所示，四边形ABCD 是菱形，∠A=60o，AB=6，点E 是边AD 中点，动点F 是在线段AB 上由A →B 运动,到达B 点停止运动，102AE AD 22=+102连接EF，以EF为折痕将△AEF折叠，点A落在A’处.(1)求A’C长度最小值.(2)求A’的路径长.例2.如图所示矩形ABCD中，AB=8，AD=6，点E是AD边上的中点，点F是AB边上的动点，连接EF，以EF为折痕将△AEF折叠，点A落在A’处，求△A’BC的面积最小值.定角定弦引圆（隐圆）：如图所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=a.像这类动点处存在一个角度恒为定角，且该角能放在一个三角形内，所对边为定边，那么该动点就是在圆上运动；这个定角就可以理解为圆周角，它所对的定边就是该圆周角所对的弦.（1）直角类型：如图1所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=90o，根据上面定角定弦可知，∠P是圆周角，AB是它所对弦，因为∠P=90o，图1 图2（2）锐角类型:如图1所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=a,且a<90o，根据上面定角定弦可知，∠P是圆周角，AB是它所对弦，此时的AB并不是直径，我们知道想要画出这个P所在的圆我们需要圆心和半径，或者找到直径；因为A，P，B三点都是圆上的点，∠A，∠B也是圆周角，点P在运动的时候∠A，∠B的大小是会发生改变的，，如图2所示.图1 图2（3）钝角类型：如图1所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=a,且a>90o，根据上面定角定弦可知，∠P是圆周角，AB是它所对弦,此时我们发现钝角是无法构造到直角三角形中去的，那么我们就要想办法去转化，我们可以通过四点共圆的特点去转化，我们可以图1 图2图3例1. 如图所示，在矩形ABCD 中AB=8，AD=6，点Q 是边AD 边上一动点，连接CQ ，过点D 作DP ⊥CQ ，交CQ 于点P .(1) 求线段BP 最小值.(2) 如图2所示，点M 也是边AD 上的动点，求BM+PM 最小值.(3) 如图2所示，点M 是边AD 上的动点，求AM+PM 最小值21图1 图2例2.在三角形ABP中，AB=6，∠P=60o，求AP+BP最大值.例3.在等边三角形ABC中，D、E分别为边AC，AB上的动点，且AD=BE；BC=6，连接CE、BD交于点F.（1）.求∠CFD.（2）.求AF最小值.2.瓜豆原理引圆：瓜豆原理：从动点的运动状态与主动点吻合（主动点在直线上运动，从动点就会在直线上运动；主动点在圆上运动，从动点就会在圆上运动）(1)如图所示点A 、B 都是定点，点D 是圆B 上一动点，连接AD ，取AD 上一点E ，使=k ，此时点D 在圆B 上运动的时候就会带着点E 一起运动，那么点D 就是主动点，点E 就是从动点；（圆B 大小不变，k 为定值）∵=k （主动点与从动点之间的关联所在）∵点A 是定点∴我们可以将点E 所在图形是点D 所在图形关于点A 位似得到的如下图：圆的位似可以对其半径进行位似，即取AB 上一点C ，使=k ∵∠A=∠A ，==k ，∴△ABD ∽△ACE ，∴==k∴CE=kBD 为定值；所以点E 就是以点C 为圆心CE 为半径的圆上运动AD AEAD AEAB ACAD AE AB AC BD CE ABAC(2).如图所示，点A 、B 是平面内定点，点D 是圆B 上一动点，∠DAE=a ，=k ，此时点D 在圆B 上运动的时候就会带着点E 一起运动，那么点D 就是主动点，点E 就是从动点；（圆B 大小不变，k 为定值，a 角度为定值）这个可以看成（1）中图形旋转得到的；取AB 上一点C ，使=k ，将AC 以点A 为旋转中心逆时针旋转a得到C ’,易证△ACE ’∽△ABD ，所以==k ，即C ’E=kBD 所以点E 为C ’为圆心C ’E 为半径的圆上运动例1．如图，点A ，B 的坐标分别为(60)(06)A B C ，，，，为坐标平面内一点，BC M 为线段AC 的中点，连接OM ，当OM 取最大值时，点M 的坐标为__________________． AD AEAB ACBD E C'ABAC2．如图，△ACB中，CA＝CB＝4，∠ACB＝90°，点P为CA上的动点，连BP，过点A作AM⊥BP于M．当点P从点C运动到点A 时，线段BM的中点N运动的路径长为。

微专题22 “隐形圆”问题考题导航题组一 利用圆的定义(到定点的距离等于定长的点的轨迹)确定隐形圆1. ⎝⎛⎭⎫－65，0 解析：由题意得圆(x －2a)2＋(y －a －3)2＝4与圆x 2＋y 2＝1相交，所以2－1<（2a ）2＋（a ＋3）2<1＋2，1<5a 2＋6a ＋9<9，⎩⎪⎨⎪⎧5a 2＋6a ＋8>0，5a 2＋6a<0，解得a ∈⎝⎛⎭⎫－65，0. 2. 2－22≤a ≤2＋22解析：因为PA 、PB 与O 相切，且∠APB ＝60°，则∠APO ＝30°，所以OP ＝OA sin 30°＝2，则存在使∠APB ＝60°的点P 等价于在圆M 上存在与点O 距离为2的点．圆M ：(x －a)2＋(y －a ＋4)2＝1的圆心M(a ，a －4)在直线y ＝x －4上，所以OM ＝a 2＋（a －4）2，所以圆M 上到点O 的最小距离为OM －1＝a 2＋（a －4）2－1，最大距离为OM ＋1＝a 2＋（a －4）2＋1，存在满足题意有点P 即OM －1≤2≤OM ＋1，解不等式得2－22≤a ≤2＋22.1. 8 解析：设A(x 1，y 1)，B(x 2，y 2)，AB 中点M(x′，y′)．因为x′＝x 1＋x 22，y′＝y 1＋y 22，所以OA →＋OB →＝(x 1＋x 2，y 1＋y 2)＝2OM →，因为C ：x 2＋y 2－6x ＋5＝0，所以(x －3)2＋y 2＝4.圆心C(3，0)，半径CA ＝2，因为点A ，B 在圆C 上，AB ＝23，所以CA 2－CM 2＝⎝⎛⎭⎫12AB 2，即CM ＝1.点M 在以C 为圆心，半径r ＝1的圆上，所以OM ≤OC ＋r ＝3＋1＝4，所以|OA →＋OB →|≤8.题组二 已知定点A ，B ，动点P 满足PA →·PB →＝λ确定隐形圆1. []4，6 解析：圆C ：(x －3)2＋(y －4)2＝1的圆心C(3，4)，半径r ＝1，设P(a ，b)在圆C 上，则AP →＝(a ＋m ，b)，BP →＝(a －m ，b)，因为∠APB ＝90°，所以AP →⊥BP →，所以AP →·BP→＝(a ＋m)(a －m)＋b 2＝0，所以m 2＝a 2＋b 2＝OP 2，所以m 的最大值即为OP 的最大值，等于OC ＋r ＝5＋1＝6，最小值为OC －r ＝5－1＝4，所以m 的取值范围是[4，6]．2. (－∞，2) 解析：由点P 在直线3x －4y ＋3＝0上，设P ⎝⎛⎭⎫x ，3x ＋34，AP →＝⎝⎛⎭⎫x －2，3x ＋34－3，BP →＝⎝⎛⎭⎫x －6，3x ＋34＋3，所以AP →·BP →＝(x －2)(x －6)＋⎝⎛⎭⎫3x ＋342－9＝116(25x 2－110x ＋57)．又AP →·BP →＋2λ＝0，所以116(25x 2－110x ＋57)＋2λ＝0，所以Δ＝(－110)2－4×25×(57＋32λ)>0，解得λ<2，所以实数λ的取值范围是(－∞，2)．1. [2，32] 解析：由题意得ax ＋a ＋c 2y ＋c ＝0，所以a(2x ＋y)＋c(y ＋2)＝0，令⎩⎪⎨⎪⎧2x ＋y ＝0，y ＋2＝0，解得x ＝1，y ＝－2，所以直线l ：ax ＋by ＋c ＝0，恒经过定点M(1，－2)．因为PH ⊥l ，点H 在以PM 为直径的圆上，其圆心C(0，－1)，圆的方程为x 2＋(y ＋1)2＝2.QC ＝22，所以QC －r ≤QH ≤QC ＋r ，线段QH 的取值范围是[2，32]．题组三 两定点A ，B ，动点P 满足PA 2＋PB 2是定值确定隐形圆1. [0，3] 解析：设M(x ，y)，因为MA 2＋MO 2＝10，所以x 2＋(y －2)2＋x 2＋y 2＝10，所以x 2＋(y －1)2＝4，因为圆C 上存在点M ，满足MA 2＋MO 2＝10，所以两圆相交或相切，所以1≤a 2＋（a －3）2≤3，所以0≤a ≤3.1. 解析：(1) 圆C 的标准方程为(x －2)2＋y 2＝4，所以圆心C(2，0)，半径为2.因为l ∥AB ，A(－1，0)，B(1，2)，所以直线l 的斜率为2－01－（－1）＝1， 设直线l 的方程为x －y ＋m ＝0，则圆心C 到直线l 的距离为d ＝|2－0＋m|2＝|2＋m|2. 因为MN ＝AB ＝22＋22＝22，CM 2＝d 2＋⎝⎛⎭⎫MN 22，所以4＝（2＋m ）22＋2， 解得m ＝0或m ＝－4，故直线l 的方程为x －y ＝0或x －y －4＝0.(2) 假设圆C 上存在点P ，设点P(x ，y)，则(x －2)2＋y 2＝4，PA 2＋PB 2＝(x ＋1)2＋(y －0)2＋(x －1)2＋(y －2)2＝12，即x 2＋y 2－2y －3＝0，即x 2＋(y －1)2＝4，因为|2－2|<（2－0）2＋（0－1）2<2＋2，所以圆(x －2)2＋y 2＝4与圆x 2＋(y －1)2＝4相交，所以点P 的个数为2.题组四 两定点A ，B ，动点P 满足PA PB＝λ(λ>0，λ≠1)确定隐形圆(阿波罗尼斯圆) 1. (x ＋1)2＋y 2＝4 解析：点M(x ，y)到O 点距离为x 2＋y 2，到A 点距离为（x －3）2＋y 2，因为到两点的距离比为12所以有x 2＋y 2（x －3）2＋y 2＝12，化简得(x ＋1)2＋y 2。

发现发现““隐形隐形””圆 巧求最小值在近几年的中考数学试题中，常有一些涉及到求线段最小值的问题.这些题目入手较难，得分率很低，分析其原因不难发现，学生对题目中运动变化的本质没有搞清楚.在这些蕴含运动变化的问题中，并没有显性的圆，但是仔细分析题目的条件，如果能发现某个点的运动路径是一个圆(或是一段弧)，可谓是“山重水复疑无路，柳暗花明又一村”，将会对问题的解决起着重要的作用.下面举例说明.一、翻折中的“隐形”圆例1 如图1，在Rt ABC ∆中，90,6,8C AC BC ∠=°==，点F在边AC 上，并且2CF =，点E 为边BC 上的动点，将CEF ∆沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是 .解 如图2，当点E 在BC 上运动时, PF 的长固定不变，即2PF CF ==.所以点P 在 以点F 为圆心，以2为半径的圆上运动.过点F 作FH AB ⊥交⊙F 于点P ，垂足为H ，此时PH 最短.由AFH ABC ∆∆:，得FH FA BC AB=.又由已知易得4,10AF AB ==.所以4810FH =，即165FH =.所以P 到AB 距离的最小值166255PH FH FP =−=−=.点评 本题关键的地方在于抓住无论点E 的位置在哪，翻折,FCE PF ∆的长度始终等 于FC 的长度，即2PF =.也就是说动点P 到定点F 的距离是定值2，所以点F 的运动路径是以点F 为圆心，2为半径的圆(或部分).如此，这个问题就最终转化为在圆上找一个到定直线距离最短的点.我们可以利用图3的模型1来作出直观解释.模型1 如图3，直线m 与⊙O 相离，过D 点O 作直线m 的垂线，垂足为点H ，交⊙O 与点P 、点Q ，则⊙O 上点P 到直线m 的距离最短，点Q 到直线m 的距离最长理由简述 在⊙O 上任意找一点P ′，过P ′作P H ′′⊥直线m ，垂足为点H ′.由三角形三边关系及直角三角形斜边大于直角边可得:OP P H OH OH ′′′′+>>，而OH OP PH =+,OP OP ′=，所以P H PH ′′>，所以点P 到直线m 的距离最短.类似的方法可以说明点P 到直线m 的距离最长.例2如图4，在边长为2的菱形ABCD 中，60,A M ∠=°对是AD 边的中点，N 是AB 边上一动点.将AMN ∆沿MN 所在的直线翻折得到A MN ′∆，连结A C ′，则A C ′长度的最小值是 .解 当点N 在AB 边上运动时，MA ′的长度固定不变，即1MA MA ′==，所以点A ′在以点M 为圆心，1为半径的圆上运动，如图5，连接CM ，与⊙M 交于点A ′，此时CA ′最短.过点C 作CG AD ⊥交AD 的延长线于点G .因为2,60CD CDG A =∠=∠=°，所以1,DG CG ==，在Rt CMG ∆中，由勾股定理，得CM == 点评 同例1，无论N 点在何处，沿MN 翻折后，线段MA ′的长度(1MA MA ′==)保持不变，而且点M 是定点，所以点A ′的运动轨迹是以M 为圆心，1为半径的圆(部分).要求A C ′的最小值，回归到模型1中，连结圆外定点C 与圆心M 与圆M 交于点A ′，此时A C ′的长度即为最小值.我们可以借助图6利用模型2来作出直观解释.模型2 如图6，点P 为⊙O 外一定点，连结PO 交⊙O 于点A ，延长线与⊙O 交于另一点B ，则PA 的长度为⊙O 外一点P 到⊙O 的最短距离，PB 的长度为⊙O 外一点P 到⊙O 的最长距离.理由简述 在⊙O 上再任意找一点A ′ ,连接PA ′，由三角形三边关系，可得OA PA OP ′′+>.又,OP OA AP OA OA ′=+=，所以PA PA ′>.类似的方法可以说明PB 的长度为⊙O 外一点P 到⊙O 的最长距离.例3 如图7，菱形ABCD 的边8,60AB B =∠=°,P 是AB 上一点，3,BP Q =是CD 边上一动点，将梯形APQD 沿直线PQ 折叠, A 的对应点为A ′.当 CA ′的长度最小时，CQ 的长为 .解 如图8，过C 作CE AB ⊥，连结AC .因为ABCD 是菱形，60B ∠=°，所以ABC ∆为等边三角形，所以84,3,12AE EB BP EP =====.要使CA ′的长度最小，则梯形APQD 沿直线PQ 折叠后A 的对应点A ′应落在CP 上，且对称轴PQ 应满足//PQ DE .由作图知，DEPQ 为平行四边形，所以1,817DQ EP CQ CD DQ ===−=−=.点评 点Q 在线段CD 上无论运动到何处，梯形APQD 沿直线PQ 折叠后PA ′的长度始终保持不变，因此A ′点的运动路径就是以点P 为圆心，PA 长为半径的圆.借助模型2，可知，当点A ′落在线段CP 与⊙P 的交点时，CA ′的长度最小.由PQ 平分,//APC CD AB ∠，可得CQ CP =.作CE AB ⊥，构造Rt CEP ∆，从而可以求出CP 的长.二、直角中的“隐形”圆例4 如图9，在正方形ABCD 中，动点,E F 分别从,D C 两点同时出发，以相同的速度在直线,DC CB 上移动.连结AE 和DF 交于点P ,由于点,E F 的移动，使得点P 也随之运动，请你画出点P 运动路径的草图.若2AD =,试求出线段CP 的最小值.解 由题意，可得DE CF =.又因为,90AD CD ADC DCB =∠=∠=°,所以ADE DCF ∆≅∆,所以DAE CDF ∠=∠.因为90ADP CDF ∠+∠=°，所以90DAE ADP ∠+∠=°.由于点P 在运动中保持90APD ∠=°.听以点P 的路径是一段以AD 为直径的弧.设AD 的中点为O ，连结OC 交弧于点P ，此时CP 的长度最小.在Rt ODC ∆中，OC ===，所以1CP OC OP =−=−. 点评 此题的本质是抓住动点,E F 在运动过程中，始终保持AE DF ⊥，即90APD ∠=°,这样点P 的运动路径就确定了，即点P 在以AD 为直径的圆弧上，再根据模型2求解即可.例5如图10, Rt ABC ∆中，,6,4,AB BC AB BC P ⊥==是ABC ∆内部的一个动点，且满足PAB PBC ∠=∠，则线段CP 长的最小值为 .解 因为90ABC ∠=°,所以90ABP PBC ∠+∠=°.又因为PAB PBC ∠=∠,所以90BAP ABP ∠+∠=°，即90APB ∠=°，所以点P 在以AB 为直径的⊙O 上.连结OC 交⊙O 于点P ，此时PC 最小，在Rt BCO ∆中，90,4,3OBC BC OB ∠=°==，可得5OC =,所以532PC OC OP =−=−=，即PC 最小值为2.点评 首先，根据题目的条件不难得出90APB ∠=°，从而可以证明点P 在以AB 直径的⊙O 上.利用模型2，连结OC ，与⊙O 交于点P ，此时PC 最小，利用勾股定理求出OC即可解决问题.以上例题说明，在求一类线段最值问题中，如果遇到动点的运动路径是圆时，只需利用上面提到的模型1或模型2就可以解决.然而难点在于如何知道动点的运动路径是圆，如何将这个隐身“圆”找出来?从以上例子中可以得出以下两种方法:①观察到定点的距离，即圆是到定点距离等于定长的点的集合;②“定弦对定张角”，如例5中线段AB是定值，当动点P在运动过程中，APB∠的大小不变等于90°(当然不一定为直角)，点P的运动路径也是圆(或弧).因此，教师在教学时，要让学生理解概念的本质，还要培养学生对常见模型的敏感性，从而在有限的考试时间内，能快速获得破解难题的策略.。

专题11 隐圆问题直线与圆是高中数学的C 级知识点，是高中数学中数形结合思想的典型体现．但有些时候，在条件中没有直接给出圆方面的信息，而是隐藏在题目中的，要通过分析和转化，发现圆（或圆的方程），从而最终可以利用圆的知识来求解，我们称这类问题为“隐形圆”问题类型一 利用圆的定义（到定点的距离等于定长的点的轨迹）确定隐形圆典例1 如果圆22(2)(3)4x a y a -+--=上总存在两个点到原点的距离为1，则实数a 的取值范围是________【答案】605a -<<【解析】到原点的距离为1的点的轨迹是以原点为圆心的单位圆，转化到此单位圆与已知圆相交求解2121-<<+∴605a -<<类型二 由圆周角的性质确定隐形圆典例 2 已知圆22:5,,O x y A B +=为圆O 上的两个动点，且2,AB M =为弦AB 的中点，()(),2C a D a +.当,A B 在圆O 上运动时，始终有CMD ∠为锐角，则实数a 的取值范围为__________．【答案】()(),20,-∞-⋃+∞【解析】由题意得2OM ==， ∴点M 在以O 为圆心，半径为2的圆上．设CD 的中点为N ，则()1N a +，且2CD =． ∵当,A B 在圆O 上运动时，始终有CMD ∠为锐角，∴以O 为圆心，半径为2的圆与以()1N a +为圆心，半径为1的圆外离．3>，整理得()211a +>， 解得2a <-或0a >．∴实数a 的取值范围为()(),20,-∞-⋃+∞．类型三 两定点A 、B ，动点P 满足(0,1)PAPBλλλ=>≠确定隐形圆（阿波罗尼斯圆） 典例3 一缉私艇巡航至距领海边界线l （一条南北方向的直线）3.8 海里的A 处，发现在其北偏东30°方向相距4 海里的B 处有一走私船正欲逃跑，缉私艇立即追击．已知缉私艇的最大航速是走私船最大航速的3 倍．假设缉私艇和走私船均按直线方向以最大航速航行．（1）若走私船沿正东方向逃离，试确定缉私艇的追击方向，使得用最短时间在领海内拦截成功；（参考数据： sin17 5.7446︒≈≈ ）（2）问：无论走私船沿何方向逃跑，缉私艇是否总能在领海内成功拦截？并说明理由．【答案】（1）略（2）能 【解析】：（1）略 （2）如图乙，以A 为原点，正北方向所在的直线为y 轴建立平面直角坐标系xOy ．则(2,B ，设缉私艇在P (x ，y )处（缉私艇恰好截住走私船的位置）与走私船相遇，则3PAPB=3=,229944x y ⎛⎫⎛-+= ⎪ ⎝⎭⎝因为圆心94⎛⎝到领海边界线l ：x = 3.8的距离为1.55，大于圆半径32所以缉私艇能在领海内截住走私船．1．已知ABC ∆中，AB AC == ABC ∆所在平面内存在点P 使得22233PB PC PA +==，则ABC∆面积的最大值为__________．【解析】设2BC a =，以BC 所在直线为x 轴、其中垂线OA 所在直线为y 轴建立直角坐标系（如图所示），则()()(,0,,0,B a C a A -，设(),P x y ，由22233PB PC PA +==，得222((3{ (1x x yy y x +++=+=，即22222232{31x y a x y a +=-+-+-=，则2722{ 11a y -=≤≤，则()()222323aa --≤≤-+即()()2222272323223232a a a a a ---≤-≤-+-， 解得234a ≤，即2241523233216ABC S a a a a ∆=⨯⨯-=-≤，即ABC ∆面积的最大值为52316.2．在平面直角坐标系xOy 中，已知B ，C 为圆224x y +=上两点， 点A(1,1)，且AB ⊥AC ，则线段BC 的长的取值范围为_______ 【答案】[62,62]-+ 【解析】设BC 的中点为M (x,y)，,因为22222OB OM BM OM AM =+=+，所以22224(1)(1)x y x y =++-+-，化简得22113222x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，所以点M 的轨迹是以11,22⎛⎫⎪⎝⎭32为半径的圆，所以AM 的取值范围是6262-+⎣⎦，所以BC 的取值范围是[62,62]．3．在平面直角坐标系xOy 中，已知圆()(22:161C x y -+-=和两点()(),2,,2A a a B a a ---，且1a >，若圆C 上存在两个不同的点,P Q ，使得90APB AQB ∠=∠=︒，则实数a 的取值范围为__________． 【答案】17117a ≤+【解析】原问题等价于以,A B 为圆心的圆与圆C 有两个交点，AB 中点坐标为()0,0，以,A B 为圆心的圆的半径1R = 且圆C 的圆心为(，半径为21R =，两圆的圆心距为： 5d ==， 结合1a >可得关于实数a 的不等式组：15 15≤≥，求解关于实数a的不等式组可得实数a的取值范围为11a ≤≤4．在平面直角坐标系xOy 中，已知点A （1-，0），B （1，0）均在圆C ： ()()22234x y r -+-=外，且圆C 上存在唯一一点P 满足AP BP ⊥，则半径r 的值为____． 【答案】4【解析】根据题意,点A(−1,0),B(1,0)，若点P 满足AP BP ⊥， 则点P 在以AB 为直径的圆上，设AB 的中点为M,则M 的坐标为 (0,0)， |AB|=2， 则圆M 的方程为221x y +=，若圆C 上存在唯一一点P 满足AP BP ⊥，则圆C 与圆M 只有一个交点，即两圆外切，则有5=，解可得r=4.5．已知等边ABC ∆的边长为2，点P 在线段AC 上，若满足等式•PA PB λ=的点P 有两个，则实数λ的取值范围是_____． 【答案】104λ-<≤ 【解析】以AB 中点为坐标原点，AB 所在直线为x 轴建立直角坐标系，则()()(()10,10,,,A B C P x y -，，，AC：()10y x =-≤≤由•PA PB λ=得221x y λ-+= ，()22111,1010044λλλ∴>-=-≤-+-=∴-<≤⎝⎭6.已知圆O ：x 2＋y 2＝1，圆M ：(x －a)2＋(y －a ＋4)2＝1.若圆M 上存在点P ，过点P 作圆O 的两条切线，切点为A ，B ，使得∠APB＝60°，则实数a 的取值范围为____________． 【答案】⎣⎢⎡⎦⎥⎤2－22，2＋22【解析】设P(x ，y)，sin ∠OPA ＝sin30°＝1x 2＋y2，则x 2＋y 2＝4 ①.又P 在圆M 上，则(x －a)2＋(y －a＋4)2＝1 ②.由①②得1≤a 2＋（a －4）2≤3，所以4－22≤a ≤4＋22.7.在平面直角坐标系xOy 中，已知过原点O 的动直线l 与圆C ：x 2＋y 2－6x ＋5＝0相交于不同的两点A ，B ，若点A 恰为线段OB 的中点，则圆心C 到直线l 的距离为____________．【答案】364【解析】∵ 圆C 1：x 2＋y 2－6x ＋5＝0，整理，得其标准方程为(x －3)2＋y 2＝4，∴ 圆C 1的圆心坐标为(3，0)；设直线l 的方程为y ＝kx ，A(x 1，y 1)，B(x 2，y 2)，联立(x －3)2＋y 2＝4，y ＝kx ，消去y 可得(1＋k 2)x2－6x ＋5＝0，由题知x 1＝12x 2, y 1＝12y 2，由韦达定理化简可得k 2＝35，即k ＝±155，直线l 的方程为y ＝±155x ，由点到直线的距离公式知，所求的距离为364.8.在平面直角坐标系xOy 中，过点P(－2，0)的直线与圆x 2＋y 2＝1相切于点T ，与圆(x －a)2＋(y －3)2＝3相交于点R ，S ，且PT ＝RS ，则正数a 的值为____________． 【答案】4【解析】圆x 2＋y 2＝1半径为1，PO ＝2，则直线PT 的倾斜角为30°，则直线方程为x －3y ＋2＝0，PT ＝3，RS ＝3，圆(x －a)2＋(y －3)2＝3的半径为3，则圆(x －a)2＋(y －3)2＝3的圆心(a ，3)到直线PT 的距离为32，由点到直线距离公式得|a －1|＝3，则正数a ＝4.9.在平面直角坐标系xOy 中，圆M ：(x －a)2＋(y ＋a －3)2＝1(a ＞0)，点N 为圆M 上任意一点．若以N 为圆心，ON 为半径的圆与圆M 至多有一个公共点，则a 的最小值为__________． 【答案】3【解析】根据题意，圆M 与以N 为圆心的圆的位置关系是内切或内含．则d MN ≤d ON －1，即1≤d ON －1.所以d ON ≥2恒成立．因为N 在圆M 上运动，所以d ON 的最小值为d OM －1，即d OM －1≥2，所以a 2＋（3－a ）2≥3，解得a≥3，所以a 的最小值为3.10.已知线段AB 的长为2，动点C 满足CA →·CB →＝λ(λ为常数)，且点C 总不在以点B 为圆心，12为半径的圆内，则实数λ的最大值是__________． 【答案】－34【解析】建立平面直角坐标系，B(0，0)，A(2，0)，设C(x ，y)，则CA →·CB →＝x(x －2)＋y 2＝λ，则(x －1)2＋y 2＝λ＋1，得（x －1）2＋y 2＝λ＋1，点C 的轨迹是以(1，0)为圆心λ＋1为半径的圆且与x 2＋y 2＝14外离或相切．所以λ＋1≤12，λ的最大值为－34. 11.在平面直角坐标系xOy 中，设直线y ＝－x ＋2与圆x 2＋y 2＝r 2(r ＞0)交于A ，B 两点．若圆上存在一点C ，满足OC →＝54OA →＋34OB →，则r 的值为________．【答案】10【解析】OC →2＝⎝ ⎛⎭⎪⎫54OA →＋34OB →2＝2516OA →2＋2·54OA →·34OB →＋916OB →2，即r 2＝2516r 2＋158r 2cos ∠AOB ＋916r 2，整理化简得cos ∠AOB ＝－35，过点O 作AB 的垂线交AB 于D ，则cos ∠AOB ＝2cos 2∠AOD －1＝－35，得cos 2∠AOD ＝15.又圆心到直线的距离为OD ＝22＝2，所以cos 2∠AOD ＝15＝OD 2r 2＝2r 2，所以r 2＝10，r ＝10.12.已知圆M ：(x －1)2＋(y －1)2＝4，直线l ：x ＋y －6＝0，A 为直线l 上一点．若圆M 上存在两点B ，C ，使得∠BAC＝60°，则点A 横坐标的取值范围是__________． 【答案】[1，5]【解析】圆M ：(x －1)2＋(y －1)2＝4上存在两点B ，C ，使得∠BAC＝60°，说明点A(x ，y)到M (1，1)的距离小于等于4，即(x －1)2＋(y －1)2≤16，而y ＝6－x ，得x 2－6x ＋5≤0，即1≤x≤5.点A 横坐标的取值范围为[1，5]．13.已知点A(0，2)为圆M ：x 2＋y 2－2ax －2ay ＝0(a ＞0)外一点，圆M 上存在点T 使得∠MAT＝45°，则实数a 的取值范围是________________． 【答案】3－1≤a＜1【解析】点A(0，2)在圆M ：x 2＋y 2－2ax －2ay ＝0(a ＞0)外，得4－4a ＞0，则a ＜1.圆M 上存在点T 使得∠MAT ＝45°，则AM2≤r ＝2a ，即AM≤2a，(a －2)2＋a 2≤4a 2(a ＞0)，解得3－1≤a.综上，实数a 的取值范围是3－1≤a＜1.14.在平面直角坐标系xOy 中，已知圆O 1，圆O 2均与x 轴相切且圆心O 1，O 2与原点O 共线，O 1，O 2两点的横坐标之积为6，设圆O 1与圆O 2相交于P ，Q 两点，直线l ：2x －y －8＝0，则点P 与直线l 上任意一点M 之间的距离的最小值为____________． 【答案】855－ 6【解析】设圆O 1的方程为(x －a)2＋(y －ka)2＝k 2a 2①，圆O 2的方程为⎝ ⎛⎭⎪⎫x －6a 2＋⎝⎛⎭⎪⎫y －6k a 2＝36k2a 2 ②，②－①，得2ax －12a x ＋2aky －12a ky ＋36a 2－a 2＝0，即2x ＋2y －a －6a ＝0.设P(x 0，y 0)，则(x 0－a)2＋(y 0－ka)2＝k 2a 2，即x 20＋y 20＝2ax 0＋2ay 0－a 2，又2x 0＋2y 0－a －6a＝0，可得2ax 0＋2ay 0－a 2＝6，故x 20＋y 20＝6，即点P 的轨迹是以原点为圆心，半径为6的圆，则点P 与直线l 上任意一点M 之间的距离的最小值为855－ 6.15.已知直线l 过点P(1，2)且与圆C ：x 2＋y 2＝2相交于A ，B 两点，△ABC 的面积为1，则直线l 的方程为________________．【答案】x －1＝0，3x －4y ＋5＝0【解析】由S △ABC ＝12×2×sin ∠ACB ＝1，sin ∠ACB ＝1，∠ACB ＝90°，则点C(0，0)到直线l 的距离为1，设直线l 的方程为y －2＝k(x －1)，利用距离公式可得k ＝34，此时直线l 的方程为3x －4y ＋5＝0，当k 不存在时，x －1＝0满足题意．16.在平面直角坐标系xOy 中，已知圆C ：x 2＋(y －1)2＝5，A 为圆C 与x 轴负半轴的交点，过A 作圆C 的弦AB ，记线段AB 的中点为M.若OA ＝OM ，则直线AB 的斜率为________． 【答案】2【解析】设点B(x 0，y 0)，则M ⎝⎛⎭⎪⎫x 0－22，y 02，圆x 2＋(y －1)2＝5与x 轴负半轴的交点A(－2，0)，OA ＝OM ＝2＝⎝ ⎛⎭⎪⎫x 0－222＋⎝ ⎛⎭⎪⎫y 022，即⎝ ⎛⎭⎪⎫x 0－222＋⎝ ⎛⎭⎪⎫y 022＝4.又 x 20＋(y 0－1)2＝5，两式相减得y 0＝2x 0＋4.而A(－2，0)也满足y 0＝2x 0＋4，即直线AB 的方程为y 0＝2x 0＋4，则直线AB 的斜率为2.17.在平面直角坐标系xOy 中，圆C 1：(x ＋1)2＋(y －6)2＝25，圆C 2：(x －17)2＋(y －30)2＝r 2.若圆C 2上存在一点P ，使得过点P 可作一条射线与圆C 1依次交于点A 、B ，满足PA ＝2AB ，则半径r 的取值范围是______________． 【答案】[5，55]【解析】在圆C 2上任取一点P ，过点P 可作一条射线与圆C 1依次交于点A 、B ，当AB 过圆心时，此时PA 在该点处最小，AB 在该点情况下最大，此时在P 点情况下PAPB 最小，当P ，A ，B 三点共线时，如图1，2，PA 为所有位置最小，且PA AB 是所有位置中最小，所以只要满足PAAB ≤2，即满足题意，错误! 5≤r ≤55.18.直角坐标系xOy 中，圆C 的方程为(x －1)2＋(y －1)2＝9，直线l ：y ＝kx ＋3与圆C 相交于A 、B 两点，M 为弦AB 上一动点，以M 为圆心，2为半径的圆与圆C 总有公共点，则实数k 的取值范围为________．【答案】⎣⎢⎡⎭⎪⎫－34，＋∞ 【解析】以M 为圆心，2为半径的圆与圆C 总有公共点，则C 点到直线l 的距离小于1，即d ＝|k ＋2|k 2＋1≤1，解得k ≤－34.19平面直角坐标系xOy 中，已知圆C ：(x －a)2＋(y －a ＋2)2＝1，点A(0，2)，若圆C 上存在点M ，满足MA 2＋MO 2＝10，则实数a 的取值范围是________． 【答案】[0，3]【解析】设M(x ，y)，由MA 2＋MO 2＝10，A(0，2)，得x 2＋(y －1)2＝4，而(x －a)2＋(y －a ＋2)2＝1，它们有公共点，则1≤a 2＋(a －3)2≤9，解得实数a 的取值范围是[0，3]．20.平面直角坐标系xOy 中，圆C 的方程为(x －1)2＋y 2＝4，P 为圆C 上一点．若存在一个定圆M ，过P 作圆M 的两条切线PA 、PB ，切点分别为A 、B ，当P 在圆C 上运动时，使得∠APB 恒为60°，则圆M 的方程为______________． 【答案】(x －1)2＋y 2＝1【解析】∵ 当P 在圆C 上运动时∠APB 恒为60°，∴ 圆M 与圆C 一定是同心圆，∴ 可设圆M 的方程为(x －1)2＋y 2＝r 2.当点P 坐标是(3，0)时，设直线AB 与x 轴的交点为H ，则MH ＋HP ＝2，MH ＝12r ，AB ＝2×32r ，所以12r ＋2×32r ×32＝2，解得r ＝1，所以所求圆M 的方程为(x －1)2＋y 2＝1.。

“隐形圆”问题江苏省通州高级中学一、问题概括江苏省高考考试说明中圆的方程是 C 级知识点，每年都考，但有些时候，在条件中没有直接给出圆方面的信息，而是隐蔽在题目中的，要经过剖析和转变，发现圆（或圆的方程），进而最后能够利用圆的知识来求解，我们称这种问题为“隐形圆”问题．二、求解策略怎样发现隐形圆（或圆的方程）是重点，常有的有以下策略．策略一利用圆的定义（到定点的距离等于定长的点的轨迹）确立隐形圆例 1（ 1）假如圆 (x－ 2a)2＋ (y－ a－ 3)2＝ 4 上总存在两个点到原点的距离为1，则实数 a 的取值范围是． 6 0a5略解：到原点的距离为 1 的点的轨迹是以原点为圆心的单位圆，转变到此单位圆与已知圆订交求解．（2）（2016 年南京二模）已知圆O：x2＋y2＝ 1，圆 M：(x－ a)2＋(y－ a＋4)2＝ 1．若圆 M 上存在点 P，过点 P 作圆 O 的两条切线，切点为A，B，使得∠ APB＝ 60°则， a 的取值范围为．解：由题意得 OP 2，所以P在以O为圆心2 为半径的圆上，即此圆与圆M 有公共点，所以有 2 1 OM 2 1 1≤ a2 (a 4)2≤ 9 2 2≤ a ≤ 2 2 ．2 2（3）（ 2017 年苏北四市一模）已知A、 B 是圆 C : x2 y 2 1 上的动点，AB= 3，P是圆12( y 4) 21 上的动点，则PA PB 的取值范围是． [7,13]C2 : (x 3）略解：取 AB 的中点 M，则 C1M= 1，所以 M 在以 C1圆心，半径为1 的圆上，且2 2PA PB 2 PM ，转变为两圆上动点的距离的最值．（4）若对随意R，直线 l： xcos ＋ ysin ＝ 2sin( ＋)＋ 4 与圆 C： (x－m)2＋ (y－ 3 m) 26＝ 1 均无公共点，则实数m 的取值范围是． ( 1, 5)2 2略解：直线 l 的方程为： (x- 1)cos ＋ (y- 3 )sin ＝ 4，M(1, 3 )到 l 距离为4，所以 l 是以 M 为圆心半径为 4 的定圆的切线系，转变为圆M 与圆 C内含．注：直线 l ： (x- x0 0 ＝R 2 2 2 的切线系．)cos ＋ (y- y )sin 为圆 M： (x x ) (x y ) R0 0例 2（ 2017 年南通市一模）在平面直角坐标系xOy 中，已知 B，C 为圆 x2 y 2 4 上两点，点 A(1，1) ，且 AB⊥ AC，则线段 BC 的长的取值范围为．解：法一（标解）：设 BC 的中点为M x, y ，由于 OB2 OM 2 BM 2 OM 2 AM 2 ，y所以 4 x2 y22 2B M x 1 y 1 ，2 2CA化简得 x 1 y 1 3 ，2 2 2所以点 M 的轨迹是以1 1为圆心，3 2为半径的O 2，2 2圆，所以 AM 的取值范围是 62 ， 62 ，所2 2 例 2以 BC 的取值范围是 6 2 ， 6 2 ．法二：以 AB、 AC 为邻边作矩形 BACN，则 BC＝ AN ，由矩形的几何性质（矩形所在平面上的随意一点到其对角线上的两个极点的距离的平方和相等），有 OB2 OC2 OA2 ON 2，所以 ON＝ 6 ，故 N 在以 O 为圆心，半径为 6 的圆上，所以BC的取值范围是 6 2 ， 6 2 ．变式 1 （ 2014 年常州高三期末卷）在平面直角坐标系xOy 中，已知圆 O : x2 y2 16 ，点P (1, 2) ，M、N 为圆 O 上两个不一样的点，且PM PN 0，若PQ PM PN，则PQ的最小值为． 3 3 5y变式 2 已知圆 C1：x2 y2 9 ，圆C2： x2 y2 4 ，定点 A P(1, 0) ，动点A, B分别在圆 C1 和圆 C2上，知足APB 90 ，则线段 AB 的取值范围． [2 3 1, 2 3 1] BO Px x变式 3已知向量a、b、c知足a3, b 2, c 1,(a c) (b c) 0 ，则 a b 范围为．[2 3 1,2 3 1]策略二动点 P 对两定点 A、B 张角是 900（ k PA k PB 1，或 PA PB 0）确立隐形圆例 3 （1）（2014 年北京卷）已知圆C： (x 3)2 ( y 4)2 1 和两点 A( m, 0) ， B(m, 0) ，若圆上存在点P，使得APB 90 ，则 m 的取值范围是． 4,6略解：由已知以 AB 为直径的圆与圆C有公共点．（2）（海安2016 届高三上期末）在平面直角坐标系xOy 中，已知点P(- 1，0) ，Q(2 ，1) ，直线 l ：ax by c 0 此中实数a，b，c 成等差数列，若点 P 在直线 l 上的射影为H，则线段QH 的取值范围是．[ 2,3 2]解：由题意，圆心 C(1，－2)在直线 ax＋ by＋ c＝ 0 上，可得 a－ 2b＋ c＝ 0，即 c＝ 2b－a．直线 l： (2a－ b)x＋ (2b－ c)y＋ (2c－ a)＝0，即 a(2x＋ y－ 3)＋ b(4－ x)＝ 0，2x y 3 0,，可得 x＝ 4，y＝－ 5，即直线过定点M(4，－ 5)，由4 x由题意，H 在以 PM 为直径的圆上，圆心为A(5， 2)，方程为 (x－ 5)2＋ (y－ 2)2＝ 50，∵ |CA|＝4 2 ，∴ CH 最小为 5 2 － 4 2 ＝ 2 ，CH 最大为 4 2 ＋ 5 2 ＝ 9 2 ，∴线段 CH 长度的取值范围是 [ 2 ， 9 2 ] ．（3）（通州区2017 届高三下开学初检测）设m R ，直线l1：x my 0 与直线l 2： mx y 2m 4 0 交于点 P( x0 , y0 ) ，则 x0 2 y0 2 2x0的取值范围是． [12 4 10,12 4 10 ]略解： l1过定点 O(0，0)，l2过定点 A(2，- 4)，则 P 在以 OA 为直径的圆上（除掉一点），变式（ 2017 年南京二模）在平面直角坐标系xOy 中，直线 l 1： kx－ y＋ 2＝ 0 与直线 l2： x＋ky－ 2＝0 订交于点 P，则当实数k 变化时，点 P 到直线 x－ y－ 4＝ 0 的距离的最大值为． 3 2策略三两定点 A、 B，动点 P 知足 PA PB 确立隐形圆例 4 （ 1）（ 2017 年南通密卷3）已知点 A(2, 3) ，点 B(6, 3) ，点 P 在直线 3x 4 y 3 0上，若知足等式 AP BP 2 0 的点 P 有两个，则实数的取值范围是．解：设 P（x， y），则 AP (x 2, y 3) ， BP ( x 6, y 3) ，依据 AP BP 2 0 ，有 x 4y 2 13 2 13 . 由题意22圆： x 4y 2 13213 圆与直线 3x 4y3 0订交，22圆心到直线的距离 d3 4 4 0 33 132 ，所以2 .223 4（2）（ 2016 年盐城三模）已知线段 AB 的长为 2，动点 C 知足 CA CB（ 为常数），且点 C 总不在以点 B 为圆 心， 1 为半径的圆内， 则负数的最大值是.324略解：动点 C 知足方程 x 2 y 21 .策略四两定点 A 、B ，动点 P 知足 PA 2PB 2 是定值确立隐形圆例 5 （ 1）在平面直角坐标系xOy 中，已知圆 C ： (x －a)2＋ (y － a ＋2)2＝ 1，点 A(0， 2)，若圆 C 上存在点 M ，知足 MA 2＋ MO 2＝ 10，则实数 a 的取值范围是．[0，3]略解： M 知足的方程为 x2( y 2 4 ，转变为两圆有公共点1)（2）（ 2017 年南京、盐城一模）在ABC 中， A ，B ， C 所对的边分别为a,b,c ，若a2b22c28 ，则 ABC 面积的最大值为．255解：以 AB 的中点为原点， AB 所在直线为 x 轴，建系 .设 A(c, 0) ， B( c, 0) ， C( x, y) ，则由 a 2 b 2 2c 28 ，2 2得 ( x c )2 y2(x c ) y 22c28 ，即 x2y245c 2 ，224所以点 C 在此圆上， S ≤ crc 4 5 c1(45c ) 5 c≤252222 24 5 4 4 5策略五两定点 A 、 B ，动点 P 知足PA(0,1) 确立隐形圆（阿波罗尼斯圆）PB例 6（1）略解：点 P 知足圆的方程为 x 2y 24 ，转变到直线与圆订交 .（2）（ 2016 届常州一模）在平面直角坐标系xOy 中，已知圆 O ： x 2＋ y 2＝ 1，O 1：(x － 4)2＋y 2＝ 4，动点 P 在直线 x3 y b 0 上，过点 P 作圆 O ，O 1 的两条切线，切点分别为 A ， B ，若知足 PB 2PA 的点 P 有且仅有两个，则b 的取值范围． －20,43例 7（ 2017 年南通二模） 一缉私艇巡航至距领海界限限l （一条南北方向的直线） 3.8 海里的A 处，发此刻其北偏东30°方向相距 4 海里的 B 处有一走私船正欲逃跑，缉私艇立刻追击．已知缉私艇的最大航速是走私船最大航速的 3 倍．假定缉私艇和走私船均按直线方向以最大航速航行．（1）若走私船沿正东方向逃离，试确立缉私艇的追击方向，使得用最短时间在领国内拦截成功；（ 参照数据： sin17 °3 ， 33 5.7446 ）6（2）问：不论走私船沿何方向逃跑，缉私艇能否总能在领国内成功拦截？并说明原因．北 l 领海 公海B30°A解：（ 1）略(例 7)（2）如图乙，以 A 为原点，正北方向所在的直线为y 轴成立平面直角坐标系 xOy ．则B2，23 ，设缉私艇在 P(x ，y) 处（缉私艇恰巧截住走私船的地点）与走私22y船相遇，则PA3 ，即xyl( x2 3 3 ．PB2)2y2领海 公海x9 29 3 2整理得，y9 ， B444所以点 P(x ，y) 的轨迹是以点9 ，93 为圆心，4 4 603 为半径的圆．Ax2图乙由于圆心9 ，9 3 到领海界限限 l ： x的距离为，大于圆半径 3 ，4 42所以缉私艇能在领国内截住走私 船． 策略六 由圆周角的性质确立隐形圆例 8 （ 1）已知 a,b, c 分别为ABC 的三个内角 A, B, C 的对边， a 2 ，(a+b)(sinA- sinB)=(c- b)sinC 则 ABC 面积的最大值为 ． 3略解： cos∠ A＝1，∠ A＝ 60°，设ABC 的外接圆的圆心为O，外接圆的半径为 2 3，则2 3O 到 BC 的距离为3，则边 BC 上的高 h 的最大值为3+2 3= 3 ，则面积的最大值3 3 3为 3 ．（2）（ 2017 年常州一模）在△ ABC 中，∠ C＝ 45o，O 是△ ABC 的外心，若 OC mOA nOB (m，n∈ R)，则 m＋ n 的取值范围是． [ 2,1)略解：∠AOB ＝2∠ C＝ 90°，点 C 在以 O 为圆心，半径 OA 的圆上（在优弧 AB 上）．三、同步练习1．已知直线 l : x 2y m 0 上存在点 M 知足与两点 A( 2, 0) , B(2, 0) 连线的斜率之积为 1 ，则实数 m 的取值范围是． [ 2 5 ,2 5 ]2 2 2， c 0 ，则 b 的取值范围2． (2016 年泰州一模 )已知实数 a， b， c 知足 a b ca 2c为． [ 3 , 3 ]3 33．已知 ,t R ，则 (cos t 2) 2 (sin t 2) 2 的取值范围是．[2 2 1,2 2 1] 4．已知圆 C : ( x 3)2 ( y 4)2 1 和两点 A( m, 0), B(m, 0) (m 0) ．若圆 C 上存在点 P，使得PA PB 1 ，则 m 的取值范围是．[ 15, 35]7．（ 2016 年无锡一模）已知圆C : ( x 2)2 y2 4 ，线段 EF 在直线 l : y x 1 上运动，点 P 为线段 EF 上随意一点，若圆 C 上存在两点 A、 B，使得 PA PB ≤ 0 ，则线段 EF 长度的最大值是．148．如图，已知点A(－ 1,0)与点 B(1,0) ， C 是圆 x2＋ y2＝ 1 上的动点 (与点 A,B 不重合 )，连结 BC 并延伸至 D，使得 |CD |＝ |BC|，则线段 PD 的取值范围． ( 2, 2)39．在平面直角坐标系 xOy 中，已知点 A(t ，0)(t 0) ， B(t ，0) ，点 C 知足 AC BC 8 ，且点 C 到直线 l ： 3x4y 24 0 的最小距离为9，则实数 t 的值是．1510．（ 2013 年江苏卷第 17 题改编）在平面直角坐标系 xOy 中，已知点 O(0, 0) ， A(0, 3) 假如圆 C : ( x a)2 ( y 2a 4) 2 1 上总存在点 M 使得 MA 2MO ，则圆心 C 的横坐标 a 的取值范围是． [0,12]511．已知向量 a 、b 、c 知足 a2 ， b a b =3 ，若 (c 2a)(2 b 3c) 0 ，则 b c 的最大值是． 1212．设点 A, B 是圆 x 2y 2 4 上的两点，点 C(1, 0) ，假如 ACB 90 ，则线段 AB 长度的取值范围为． [7 1, 7 1]13．在 ABC 中， BC ＝ 2，AC ＝ 1，以 AB 为边作等腰直角三角形ABD (B 为直角极点， C 、D 两点在直线 AB 的双侧 )．当∠ C 变化时，线段CD 长的最大值为． 314．（ 2016 年南通三模）在平面直角坐标系xOy 中，圆 C 1 : x 122 ，y 2圆 C 1 : xm 22m2，若圆 C 2 上存在点 P 知足：过点 P 向圆 C 1 作两条切线y mPA 、 PB ，切点为 A 、 B ， ABP 的面积为 1，则正数 m 的取值范围是 ．解：设 P(x ，y) ，设 PA ， PB 的夹角为 2．△ ABP 的面积 S=1PA 2 sin 2PA 22 PA 1 ．2PC 1 PC 13PC 222 ，解得 PA2， 由 2PA 1 PA所以 PC 1 2 ，所以点 P 在圆 ( x 1)2 y 2 4 上．所以 m2 ≤ (m 1)2 ( m)2 ≤ m2 ，解得 1≤ m ≤3 2 3 ．。