2019中考-“隐形圆”问题(共22张PPT)全面.ppt
- 格式:ppt
- 大小:1.49 MB
- 文档页数:24


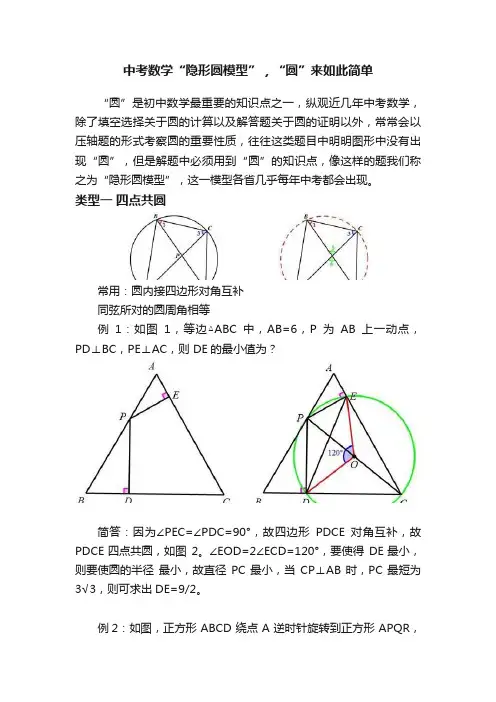
中考数学“隐形圆模型”,“圆”来如此简单“圆”是初中数学最重要的知识点之一,纵观近几年中考数学,除了填空选择关于圆的计算以及解答题关于圆的证明以外,常常会以压轴题的形式考察圆的重要性质,往往这类题目中明明图形中没有出现“圆”,但是解题中必须用到“圆”的知识点,像这样的题我们称之为“隐形圆模型”,这一模型各省几乎每年中考都会出现。
类型一四点共圆常用:圆内接四边形对角互补同弦所对的圆周角相等例1:如图1,等边△ABC中,AB=6,P为AB上一动点,PD⊥BC,PE⊥AC,则 DE的最小值为?简答:因为∠PEC=∠PDC=90°,故四边形PDCE对角互补,故PDCE四点共圆,如图2。
∠EOD=2∠ECD=120°,要使得DE最小,则要使圆的半径最小,故直径PC最小,当CP⊥AB时,PC最短为3√3,则可求出DE=9/2。
例2:如图,正方形 ABCD 绕点 A 逆时针旋转到正方形 APQR,连接 CQ,延长 BP 交于 CQ 于点 E,求证:E 是线段 CQ 的中点简答:因为 AC=AQ,AB=AP 且∠BAP=∠CAQ(旋转角相等)故△APB∽△AQC,故∠ABP=∠ACQ ,又因为∠1=∠2,故A、B、C、E 四点共圆(如图 2),因为∠ABC=90°,故 AC 是直径,故∠AEC=90°,又因为 AQ=AC,所以 AE 垂直且平分 QC(三线合一)类型二定义—动点到定点等于定长同一个端点处有多条相等线段时,要想到构造圆。
例:1:如图 1,四边形 ABCD 中,AB=AC=AD,若∠CAD=76°,则∠CBD= 度。
简答:如图 2,因为 AB=AC=AD,故 B、C、D 三点在以 A 为圆心的圆上,故∠CBD= 1/2∠CAD=38°例2:如图 1,长 2 米的梯子 AB 竖直放在墙角,在沿着墙角缓慢下滑直至水平地面过程中,梯子 AB 的中点 P 的移动轨迹长度为?.简答:由斜边上的中点等于斜边的一半可知,OP=1,动点P到定点O的距离始终等于1,满足圆的定义(到定点的距离等于定长的点的集合叫做圆),故P的运动轨迹是圆弧,圆心角为90°,轨迹长度为四分之一圆的长度。


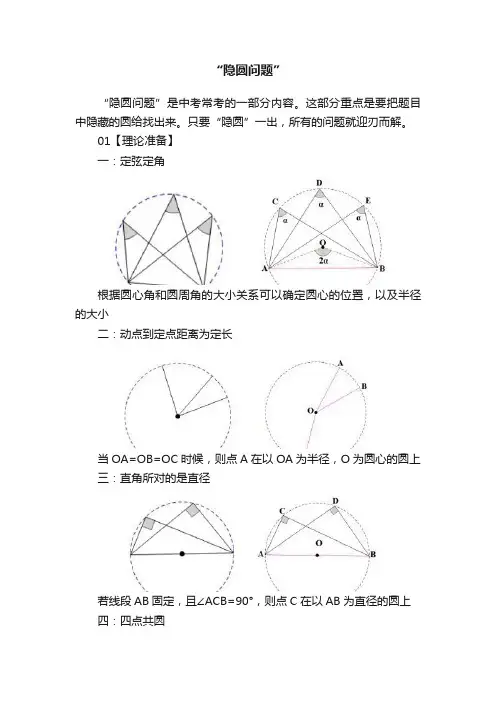
“隐圆问题”“隐圆问题”是中考常考的一部分内容。
这部分重点是要把题目中隐藏的圆给找出来。
只要“隐圆”一出,所有的问题就迎刃而解。
01【理论准备】一:定弦定角根据圆心角和圆周角的大小关系可以确定圆心的位置,以及半径的大小二:动点到定点距离为定长当OA=OB=OC时候,则点A在以OA为半径,O为圆心的圆上三:直角所对的是直径若线段AB固定,且∠ACB=90°,则点C在以AB为直径的圆上四:四点共圆可知:∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8。
△ABE∽△DCE,△ADE∽△BCE02【例题精讲】类型一:定弦定角1.如图,∠MON= 45°,线段AB=10,且A,B 分别在OM、ON 上移动,那么点O到AB的距离的最大值为__________.3.如图,△ABC为等边三角形,AB=2,若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为__________类型二:动点到定点距离为定长1.如图,长2米的梯子AB竖直放在墙角,在沿着墙角缓慢下滑直至水平地面过程中,梯子AB的中点P的移动轨迹长度为?2.如图,在矩形ABCD中,AB=2,AD=3,点E,F分别为AD、DC边上的点,且EF=2,G为EF的中点,P为BC边上一动点,则PA+PG的最小值为?类型三:直角所对的是直径1.如图,E、F是正方形ABCD的边AD上两个动点,满足AE = DF,连接CF交BD于点G,连接BE交AG于点H,若正方形的边长为2,则线段DH长度的最小值是__________.2.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且始终有AP⊥BP,则线段CP长的最小值为_________类型四:四点共圆1.如图,正方形ABCD中,∠EAF=45°,AF与BD交于N,AE与BD交于M,连接MF、NE,求证△ANE、△AMF是等腰直角三角形.2.如图,等边△ABC中,AB=6,P为AB上一动点,P D⊥BC,PE⊥AC,则DE的最小值为?03【总结】隐圆问题经常涉及和最值问题联系在一起。



2019中考数学复习隐形圆问题大全(后有专题练习无答案)2019中考数学复:隐形圆问题大全一定点+定长根据到定点的距离等于定长的点的集合是以定点为圆心定长为半径的圆的原理,可以应用到以下问题中:1.在四边形ABCD中,AB=AC=AD=2,BC=1,且AB∥CD,求BD的长度。
解析:因为AB=AC=AD=2,所以B、C、D在以A为圆心、2为半径的圆上。
又因为AB∥CD,所以DE=BC=1.根据勾股定理,易得BD=√15.2.在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是多少?解析:因为E是定点,EB′是定长,所以B′点路径为以E为圆心、EB′为半径的圆。
作穿心线DE可得B′D的最小值为2√10.3.在ΔABC中,AB=4,AC=2,以BC为边在ΔABC外作正方形BCDE,BD、CE交于点O,则线段AO的最大值为多少?解析:首先确定A、B点的位置,因为AC=2,所以C点在以A为圆心、2为半径的圆上。
因为点O是点C以点B为中心顺时针旋转45度并1:√2缩小而得,所以将圆A旋转45度再1:2缩小即可得到O点路径。
转化为求定点A到定圆F的最长路径,即AF+FO=3+2√2.二定线+定角根据与一条定线的两端夹角一定的动点路径是以定线为弦,定角为圆周角的弧的原理,可以应用到以下问题中:1.在矩形ABCD中,AB=10,AD=4,点P是CD上的动点,当∠APB=90°时求DP的长度。
解析:因为AB为定线,∠APB为定角(90°),所以P点路径为以AB为弦(直径)的弧。
根据勾股定理,可得DP为2或8.2.在等边三角形ABC中,∠XOY = 45°,点A、B分别在OX、OY上移动,且AB = 2,那么OC的最大值为多少?解析:因为AB为定线,∠XOY为定角,所以O点路径为以AB为弦所含圆周角为45°的弧。


隐形圆问题
模型一定点定长作圆
一.模型分析
1.平面内,点A为定点,点B为动点,且AB长度固定,则点B的轨迹在以点A 为圆心,AB长为半径的圆上(如图). 依据的是圆的定义:圆是所有到定点的距离等于定长的点的集合.
2.推广:如图,点E为定点,点F为线段BD上的动点(不含点B),将△BEF沿EF折叠得到△B′EF,则点B′的运动轨迹为以点E为圆心,以线段BE为半径的一段圆弧.
练习反馈
1. 如图,已知OC=3,点A、B分别是平面内的动点,且OA=2,BC=4,请在平面内画出点A、B的运动轨迹.
解:如解图,点A的运动轨迹为圆O,点B的运动轨迹为圆C.。