两点之间线段最短的应用

两之间线段最短求最值四大类型【专题说明】“两点之间，线段最短”是初中数学中的基本定理之一，也是人们在生活中认识到的基本事实，而对于数学中的最值问题，学生往往无从下手，其实往往就是这个基本定理的应用。

【方法技巧】模型一“一线两点”型(一动＋两定)类型一异侧线段和最小值问题问题：两定点A，B位于直线l异侧，在直线l上找一点P，使PA＋PB值最小．【解题思路】根据两点之间线段最短，PA＋PB的最小值即为线段AB的长．连接AB交直线l 于点P，点P即为所求．类型二同侧线段和最小值问题(将军饮马模型)问题：两定点A，B位于直线l同侧，在直线l上找一点P，使得PA＋PB值最小．【解题思路】将两定点同侧转化为异侧问题，同类型一即可解决．作点B关于l 的对称点B′，连接AB′，与直线l的交点即为点P.类型三同侧差最大值问题问题：两定点A，B位于直线l同侧，在直线l上找一点P，使得|PA－PB|的值最大．【解题思路】根据三角形任意两边之差小于第三边，|PA－PB|≤AB，当A，B，P 三点共线时，等号成立，即|PA－PB|的最大值为线段AB的长．连接AB并延长，与直线l的交点即为点P.类型四异侧差最大值问题问题：两定点A，B位于直线l异侧，在直线l上找一点P，使得|PA－PB|的值最大．【解题思路】将异侧点转化为同侧，同类型三即可解决．模型二“一点两线”型(两动＋一定)问题：点P是∠AOB的内部一定点，在OA上找一点M，在OB上找一点N，使得△PMN周长最小．【解题思路】要使△PMN周长最小，即PM＋PN＋MN值最小．根据两点之间线段最短，将三条线段转化到同一直线上即可．模型三“两点两线”型(两动＋两定)问题：点P，Q是∠AOB的内部两定点，在OA上找点M，在OB上找点N，使得四边形PQNM周长最小．【解题思路】要使四边形PQNM周长最小，PQ为定值，即求得PM＋MN＋NQ的最小值即可，需将线段PM，MN，NQ三条线段尽可能转化在一条直线上，因此想到作点P关于OA的对称点，点Q关于OB的对称点．【典例分析】【典例1-1】基本模型问题：如图，定点A，B位于动点P所在直线l同侧试确定点P的位置，使AP+BP的值最小．解题思路：一找：作点B关于直线l的对称点B'，连接AB′，与直线l交于点P；二证：验证当A，P，B'三点共线时，AP+BP取得最小值．三计算．请写出【基本模型】中解题思路“二证”的过程．【典例1-2】模型演变问题：如图，定点A，B位于动点P所在直线l同侧，在直线l上确定点P的位置，使|P A ﹣PB|的值最大．解题思路：一找：连接AB并延长，交直线l于点P；二证：验证当A，B，P三点共线时，|P A﹣PB|取得最大值．三计算．请写出【模型演变】中解题思路“二证”的过程．【典例1-3】模型演变问题：如图，定点A，B位于动点P所在直线l的两侧，试确定点P的位置，使AP+BP 的值最小．解题思路：一找：连接AB交直线l于点P；二证：验证当A，P，B三点共线时，AP+BP取得最小值．三计算．请写出【模型演变】中解题思路“二证”的过程．【典例1-4】模型演变问题：如图，定点A，B位于动点P所在直线l的两侧，试确定点P的位置，使|P A﹣PB|的值最大．解题思路：一找：作点B关于直线l的对称点B'，连接AB'并延长，交直线于点P；二证：验证当A，B'，P三点共线时，|P A﹣PB|取得最大值．三计算．请写出【模型演变】中解题思路“二证”的过程．【变式1-1】如图，已知菱形ABCD的边长为4，∠ABC＝60°，点N为BC的中点，点M是对角线AC上一点，则MB+MN的最小值为．【变式1-2】如图，在矩形ABCD中，AB＝4，BC＝6，点O是对角线BD的中点，E是AB 边上一点，且AE＝1，P是CD边上一点，则|PE﹣PO|的最大值为．【变式1-3】如图，在菱形ABCD中，AB＝12，∠DAB＝60°，对角线AC，BD交于点O，点E，F分别在BD，AB上，且BF＝DE＝4．点P为AC上一点，则|PF﹣PE|的最大值为．【变式1-4】结论：如图，抛物线y＝ax2﹣bx﹣4与x轴交于，A（﹣1，0），B（4，0）两点，与y轴交于点C，直线l为该抛物线的对称轴，点M为直线l上的一点，则MA+MC 的最小值为．【典例2】模型分析问题：点P是∠AOB内的一定点，点M，N分别为OA，OB上的动点，试确定点M，N 的位置，使△PMN的周长最小．解题思路：一找：分别作点P关于OA，OB的对称点P′，P“，连接P'P“，分别交OA，OB于点M，N；二证：验证当P′，M，N，P″四点共线时，△PMN的周长最小．三计算．注：当三个点均为动点时，先假定一个点为定点，再将其特化为“一定两动“问题请写出【模型分析】中解题思路“二证”的过程．【变式2-1】如图，在四边形ABCD中，∠BAD＝121°，∠B＝∠D＝90°，点M、N分别在BC、CD上，（1）当∠MAN＝∠C时，∠AMN+∠ANM＝°；（2）当△AMN周长最小时，∠AMN+∠ANM＝°．【变式2-2】如图，在边长为2的等边△ABC中，点P，M，N分别是BC，AB，AC上的动点，则△PMN周长的最小值为．【典例3】模型分析问题：点P，Q是∠AOB内部的两定点，点M，N分别是OA，OB上的动点，试确定点M，N的位置，使四边形PMNQ的周长最小．解题思路：一找：作点P关于OA的对称点P'，点Q关于OB的对称点Q′，连接P′Q′，分别交OA，OB于点M，N；二证：验证当P′，M，N，Q′四点共线时，四边形PQNM的周长最小．三计算．请写出【模型分析】中解题思路“二证”的过程．【变式3-1】如图，已知正方形ABCD的边长为5，AE＝2DF＝2，点G，H分别在CD，BC 边上，则四边形EFGH周长的最小值为．【变式3-2】如图，在矩形ABCD中，AB＝6，BC＝3，点E是AB的中点，若点P，Q分别是边BC，CD上的动点，则四边形AEPQ周长的最小值为．【典例4-1】基本模型问题：如图，点A，B为直线l同侧两定点，M，N为直线l上的动点，且MN的长度为定值，试确定点M，N的位置，使AM+MN+BN的值最小．解题思路：一找：以AM，MN为邻边．构造▱AMNA′，作点A′关于直线l的对称点A“，连接A “B，交直线l于点N，再确定点M；二证：验证当A“，N，B三点共线时，AM+MN+BN的值最小．三计算．请写出【基本模型】中解题思路“二证”的过程．【典例4-2】模型演变问题：如图，直线a∥b，定点A，B分别位于直线a的上方和直线b的下方，M，N分别为直线a，b上的动点，且MN⊥a，试确定点M，N的位置，使AM+MN+BN的值最小．解题思路：一找：以AM，MN为邻边构造▱AMNA′，连接A'B；二证：验证当A'，N，B三点共线时，AM+MN+BN的值最小．三计算．请写出【模型演变】中解题思路“二证”的过程．【变式4-1】如图，正方形ABCD内接于⊙O，线段MN在对角线BD上运动，若⊙O的面积为2π，MN＝1，则AM+CN的最小值为．【变式4-2】如图，在矩形ABCD中，AB＝，BC＝1，将△ABD沿射线DB方向平移得到△A'B'D'，连接B'C，D'C，求B'C+D'C的最小值．专题12 两之间线段最短求最值（四大类型含将军饮马）（知识解读）【专题说明】“两点之间，线段最短”是初中数学中的基本定理之一，也是人们在生活中认识到的基本事实，而对于数学中的最值问题，学生往往无从下手，其实往往就是这个基本定理的应用。

回归数学的本质----《“两点之间线段最短”公理的应用》教学新探一、问题的提出3月12日，植树节，一个播种希望的季节。

我校“新课程下有效课堂教学策略的研究”课题也播下了希望的种子。

作为其中的一名“植树人”，经历着课程改革的点滴风雨，感受着一线教师在课堂教学中不同教学方式的尝试与变化，从对传统教学的批判到合作学习、探究学习形式的流行，倘若把握不住学习的本质便会使我们的教学从一个极端走向另一个极端：在热闹的课堂表象下是对数学本质的流失。

中国古人对学习有着深刻的认识：在象形文字中，学上半部分是两个手把着的算筹，下半部分为一个专门的场所，引申为从书本上、教师里获取间接知识；习的上半部分是“羽”，代表雏鹰，雏鹰离开巢臼试着飞行称之为习，引申为从经验中、个体实践中获取知识。

可见学生的学习是教师与学生两者之间的有机结合，任何一方的忽视都是不可行的。

二、理论依据数学是研究客观世界的数量关系和空间形式的科学，它具有很强的概括性、抽象性和逻辑性。

数学教学是数学思维过程的教学，学生学习数学的过程是在头脑中建构认知结构的过程，是主体的一种自主行为。

它遵循着人类认识的一般规律，也有其特殊规律。

2007年4月教育部数学教育高级研修班在宁波举行会议。

华师大数学系汪晓勤副教授在这次会议中作了《历史的相似性及其教学启示》报告，报告中提到要像数学家发现问题、思考问题那样进行教学，而这一重要思想就如伟大科学家爱因斯坦给M.索洛文的信中所提及的那样，爱因斯坦把经验、直觉与理论描述为如右图的图景：从直接经验到建立公理（ε→A），这是一种直觉联系，从公理到导出命题（A →ε），那是一种逻辑必然联系，从导出命题到实际（S→ε）则是一种实践、S2S1S公理体系A导出命题直接经验ε实验验证，从中得到的经验还可修正已有的公理，如此循环往复。

三、实践研究下面从“两点之间线段最短”这一公理出发，对教学过程中的若干问题、环节进行如下的实践与探究：（一）从直接经验中得到公理浙教版《数学》（七上）的教材中是通过生活常识引入这一公理：（1） 小狗看到远处的骨头，总是径直奔向食物；（2） 从A 地到B 地有3条路可走（如图1），为了尽快到达，人们通常选择其中的直路。

2点之间线段最短的例子
1. 你看啊，从家到学校，走直线肯定是最快的呀，如果你非要绕几个弯，那不是浪费时间嘛！就像你明明可以直接走过去跟朋友说话，却非要绕一大圈，这不就跟两点之间线段最短背道而驰了嘛！
2. 想想去超市买东西，你肯定会选择最近的路直达货架呀，难道还会七拐八拐地走远路吗？这就跟两点之间线段最短一个道理呀！
3. 哎呀，运动员在赛场上跑步，肯定也是找最短的路线去冲向终点呀，要是乱拐弯，那还怎么拿好成绩，这不是明摆着两点之间线段最短嘛！
4. 你和小伙伴约好见面，肯定是想着直接过去找他，而不是绕来绕去的吧，这多简单的道理，两点之间线段最短啊！
5. 比如说送快递的小哥，他们都是选择最直接的路去送包裹呀，这样才能最快送到客户手里呀，不就是因为两点之间线段最短嘛！
6. 工作中完成一个任务，也会找最快捷的方法吧，就像从起点到终点，肯定是直着走最快呀，这就是两点之间线段最短在生活中的体现呀！
我的观点结论就是：两点之间线段最短这个道理在我们生活中无处不在呀，我们做很多事其实都在遵循这个道理呢！。

奶站问题的讨论以及解决策略奶站问题中中,关键在于，我们善于作定点关于动点所在直线的对称点，或利用平移和展开图来处理。

这对于我们解决此类问题有事半功倍的作用。

理论依据：“两点之间线段最短”，“垂线段最短”，“点关于线对称”，“线段的平移”“立体图形展开图”。

教材中的例题“饮马问题”，“造桥选址问题”“立体展开图”。

考的较多的还是“饮马问题”。

解题总思路：找点关于线的对称点实现“折”转“直”，利用平移把“折”转“直”，利用平面展开图把“折”转“直”。

一、运用轴对称解决距离最短问题利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离。

基本思路是运用轴对称及两点之间线段最短的性质，将所求线段之和转化为一条线段的长，是解决距离之和最小问题，不论题目如何变化，运用时要抓住直线同旁有两点，这两点到直线上某点的距离和最小这个核心，所有作法都相同．注意：利用轴对称解决最值问题应注意题目要求，根据轴对称的性质、利用三角形的三边关系，通过比较来说明最值问题是常用的一种方法．解决这类最值问题时，要认真审题，不要只注意图形而忽略题意要求，审题不清导致答非所问．1、两点在一条直线异侧例：已知：如图，A，B在直线L的两侧，在L上求一点P，使得PA+PB最小。

解：连接AB,线段AB与直线L的交点P ，就是所求。

（根据：两点之间线段最短.）2、两点在一条直线同侧例：图所示，要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A、B到它的距离之和最短．解：只有A、C、B在一直线上时，才能使AC+BC最小．作点A关于直线“街道”的对称点A′，然后连接A′B，交“街道”于点C，则点C 就是所求的点．应用1、（2009年达州）在边长为2㎝的正方形ABCD 中，点Q 为BC 边的中点，点P 为对角线AC 上一动点，连接PB 、PQ ，则△PBQ 周长的最小值为____________㎝（结果不取近似值）.2、(2009年抚顺市)如图所示，正方形ABCD 的面积为12，ABE △是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，使PD PE 的和最小，则这个最小值为（ ） A ．23 B ．26 C ．3 D ．63、(2009年鄂州)已知直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD =2，BC =DC =5，点P 在BC 上移动，则当P A +PD 取最小值时，△APD 中边AP 上的高为（ ） A 、17172B 、17174C 、17178D 、33、一点在两相交直线内部例：已知：如图A 是锐角∠MON 内部任意一点，在∠MON 的两边OM ，ON 上各取一点B ，C ，组成三角形，使三角形周长最小.解：分别作点A 关于OM ，ON 的对称点A ′，A ″；连接A ′，A ″，分别交OM ，ON 于点B 、点C ，则点B 、点C 即为所求分析：当AB 、BC 和AC 三条边的长度恰好能够体现在一条直线上时，三角形的周长最小4、两个点在矩形内部例：已知矩形ABCD 内有两个点M 、N ，过M 击球到CD 边P ，然后击到BC 边Q ，然后到N,则小球所走的最短路线？二、利用平移确定最短路径选址通过平移，除去固定部分的长，使其余几段的和正好为两定点之间的距离。

利用 两点之间线段最短 解决最值问题陈礼弦(贵州省贵安新区普贡中学ꎬ贵州贵安新区５６１１１３)摘㊀要:文章立足于初中数学教学实践ꎬ结合典型实例详细论述了利用 两点之间线段最短 结论解决最值问题的主要思路ꎬ旨在于为初中数学教学提供崭新思路.与此同时ꎬ通过解题活动ꎬ提高学生分析问题和解决问题的能力ꎬ提升其数学核心素养.关键词:初中数学ꎻ核心素养ꎻ线段最短ꎻ最值问题中图分类号:Ｇ６３２㊀㊀㊀文献标识码:Ａ㊀㊀㊀文章编号:１００８－０３３３(２０２４)０８－００１３－０３收稿日期:２０２３－１２－１５作者简介:陈礼弦(１９７１.１２ )ꎬ男ꎬ贵州省清镇人ꎬ本科ꎬ高级教师ꎬ从事初中数学解题研究.㊀㊀与线段之和或差有关的几何最值问题是中考热点ꎬ通常以中考压轴题的形式出现ꎬ具有一定的选拔性功能ꎬ对学生而言具有一定的难度.这类问题是教学的难点ꎬ是核心素养的重点考查对象[１].在初中数学教学中ꎬ教师该如何引导学生利用 两点之间线段最短 解决最值问题呢?根据笔者多年的教学经验ꎬ只要弄清三个数学模型ꎬ学生在解决这类问题时便会收到事半功倍之效.１模型１ 一线两点 型１.１利用 两点之间线段最短 求线段和的最小值１.１.１点在直线两侧时ꎬ线段和的最小值问题例１㊀如图１ꎬ两定点Ｃ㊁Ｄ位于直线ａ两侧ꎬ在直线ａ上找一点Ｍꎬ使得ＭＣ＋ＭＤ的值最小.图１㊀点在线段两侧示意图㊀㊀㊀图２㊀ＭＣ＋ＭＤ取最小值示意图解析㊀如图２ꎬ连接ＣＤ交直线ａ于点Ｍꎬ点Ｍ就是所找的点.理由是 两点之间线段最短 .１.１.２点在直线同侧时ꎬ线段和的最小值问题例２㊀如图３ꎬ两定点Ｃ㊁Ｄ位于直线ａ的同侧ꎬ在直线ａ上找一点Ｍꎬ使得ＭＣ＋ＭＤ的值最小.图３㊀点在直线同侧示意图㊀㊀图４㊀ＭＣ＋ＭＤ取最小值示意图解析㊀如图４ꎬ作点Ｄ关于直线ａ的对称点Ｄᶄꎬ连接ＣＤᶄ与直线ａ交于点Ｍꎬ点Ｍ就是所找的点.显然ꎬ将直线ａ同侧两个定点转化为两侧两个定点ꎬ便可以利用点在直线两侧时线段和的最小值问题的处理方法解决最值问题.１.１.３模型应用例３㊀如图５ꎬ已知әＤＥＦ中ꎬＤＥ＝ＤＥꎬＧＨ是ＤＥ的垂直平分线ꎬＭ是ＧＨ上一动点ꎬ点Ｎ是ＥＦ的中点ꎬ如果ＤＥ＝１３ꎬәＤＥＦ的周长是３６ꎬ求ＥＭ＋ＭＮ的最小值.解析㊀如图６ꎬ连接ＤＭꎬＭＮ.因为ＤＥ＝ＤＦ＝１３ꎬәＤＥＦ的周长是３６ꎬ所以ＥＦ＝３６－２ˑ１３３１图５㊀例３题图㊀㊀㊀㊀㊀㊀㊀图６㊀例３解析图＝１０.又因为Ｎ是ＥＦ的中点ꎬ所以ＥＮ＝１２ＥＦ＝５.又因为әＤＥＦ是等腰三角形ꎬ点Ｎ是ＥＦ的中点ꎬＤＮʅＥＦꎬ所以ＤＮ＝ＤＥ２－ＥＮ２＝１３２－５２＝１２.又因为ＧＨ是ＤＥ的垂直平分线ꎬ所以ＭＤ＝ＭＥꎬ所以ＥＭ＋ＭＮ＝ＤＭ＋ＭＮȡＤＮꎬ所以ＤＮ的长为ＥＭ＋ＭＮ的最小值ꎬ所以ＥＭ＋ＭＮ的最小值为１２.１.２利用 两点之间线段最短 求线段差最大值１.２.１点在直线同侧时ꎬ线段差的最大值问题例４㊀如图７ꎬ两定点ＭꎬＮ位于直线ｂ的同侧ꎬ在直线ｂ上找一点Ｈꎬ使得｜ＨＭ－ＨＮ｜的值最大.㊀图７㊀点在直线同侧示意图㊀图８㊀｜ＨＭ－ＨＮ｜的最大值示意图解析㊀如图８ꎬ连接ＭＮ并延长与直线ｂ交于点Ｈꎬ点Ｈ就是所找的点.１.２.２点在直线两侧时ꎬ线段差的最大值问题例５㊀如图９ꎬ两定点ＢꎬＣ位于直线ｌ的两侧ꎬ在直线ｎ上找一点Ｍꎬ使得︱ＭＢ－ＭＣ｜的值最大.图９㊀点在直线两侧示意图㊀㊀图１０︱ＭＢ－ＭＣ｜的最大值示意图解析㊀如图１０ꎬ作点Ｃ关于直线ｎ的对称点Ｃᶄꎬ连接ＢＣᶄ并延长与直线ｎ交于点Ｍꎬ点Ｍ就是所找的点.显然ꎬ将已知直线两侧的两个定点转化为同侧的两个定点ꎬ便可以用同侧线段差最大值的方法解决问题.１.２.３模型应用例６㊀如图１１ꎬ在正方形ＤＥＦＧ中ꎬＤＥ＝６ꎬ点Ｉ是对角线ＥＧ上靠近点Ｅ的三等分点ꎬ点Ｈ是ＤＧ边上的一点ꎬ且ＧＨ＝２.Ｊ为ＥＦ上一点ꎬ连接ＪＨ㊁ＪＩ.①在图中画ＪＨ－ＪＩ的最大值时点Ｊ的位置(为区分点Ｊꎬ请用字母Ｊ 标记)ꎻ②求ＪＨ－ＪＩ的最大值.图１１㊀例６题图㊀㊀㊀㊀㊀图１２㊀例６解析图解析㊀如图１２ꎬ连接ＨＩ并延长交ＢＣ于点Ｊᶄꎬ则点Ｊᶄ即为所求作的点.如图１２ꎬ过点Ｉ作ＩＫʅＤＧ于点Ｋꎬ延长ＫＩ交ＥＦ于点Ｌꎬ所以ＪＨ－ＪＩ的最大值即为ＨＩ的长.因为四边形ＤＥＦＧ为正方形ꎬ所以ＤＧ//ＥＦꎬＤＥ＝ＥＦ＝ＦＧ＝ＧＤ＝６ꎬ所以四边形ＤＥＬＫ是矩形ꎬәＧＨＩ为等腰直角三角形ꎬＥＧ＝６２.因为点Ｉ是对角线ＥＧ上的三等分点ꎬ所以ＧＩ＝２３ＥＧ＝４２ꎬ所以ＫＩ＝ＧＫ＝４ꎬ所以ＨＫ＝ＧＫ－ＧＨ＝２ꎬ所以ＨＩ＝ＫＩ２＋ＨＫ２＝４２＋２２＝２５.２模型２ 一定两线 型２.１利用 两点之间线段最短 求周长最小值例７㊀如图１３ꎬ点Ｄ是øＢＯＣ的内部一定点ꎬ在ＯＢ上找一点Ｎꎬ在ＯＣ上找一点Ｍꎬ使得әＤＭＮ的周长最小.解析㊀如图１４ꎬ分别作点Ｄ关于ＯＢ㊁ＯＣ的对称点Ｄᶄ㊁Ｄᵡꎬ连接ＤᶄＤᵡꎬ交ＯＢ㊁ＯＣ于点Ｎ㊁Ｍꎬ点Ｎ㊁Ｍ便是所找的点.２.２利用 两点之间线段最短 求线段和的最小值例８㊀如图１５ꎬ点Ｍ是øＤＥＦ的内部一定点Ｍꎬ在ＥＤ上找一点Ａꎬ在ＥＦ上找一点Ｂꎬ使得ＭＢ＋ＡＢ的值最小.４１图１３㊀例７题图㊀㊀㊀㊀㊀㊀图１４㊀例７解析图图１５㊀例８题图㊀㊀㊀㊀㊀㊀图１６㊀例８解析图解析㊀如图１６ꎬ作点Ｍ关于ＥＦ的对称点Ｍᶄꎬ过点Ｍᶄ作ＥＤ的垂线ꎬ分别与ＥＤ㊁ＥＦ交于点Ａ㊁Ｂꎬ点Ａ㊁Ｂ是所找的点.２.３模型应用例９㊀如图１７ꎬ在ＲｔәＢＣＤ中ꎬøＢＣＤ＝９０ʎꎬＤＣ＝６ꎬＢＣ＝８ꎬＤＥ是øＢＤＣ的平分线.若Ｍ㊁Ｎ分别是ＤＣ㊁ＤＥ上的动点ꎬ求ＮＣ＋ＮＭ的最小值.图１７㊀例９题图㊀㊀㊀㊀㊀图１８㊀例９解析图解析㊀如图１８ꎬ作点Ｍ关于ＤＥ的对称点Ｍᶄꎬ因为ＤＥ是øＢＤＣ的平分线ꎬ所以Ｍᶄ在ＤＢ上ꎬ连接ＣＭᶄꎬＮＭᶄꎬ所以ＮＭᶄ＝ＮＭꎬ所以ＮＣ＋ＮＭ＝ＮＣ＋ＮＭᶄȡＣＭᶄꎬ所以当ＣＭᶄ垂直ＡＢ时ꎬＣＭᶄ为最小值ꎬ所以ＮＣ＋ＮＭ为最小值ꎬ在ＲｔәＤＣＢꎬøＤＣＢ＝９０ʎꎬＤＣ＝６ꎬＢＣ＝８ꎬ所以ＤＢ＝ＤＣ２＋ＢＣ２＝１０ꎬ因为１２ＤＣ ＢＣ＝１２ＤＢ ＣＭᶄꎬ所以ＣＭᶄ＝２４５ꎬ所以ＮＣ＋ＮＭ的最小值为２４５.３模型３ 一定长ꎬ两定点 型３.１异侧线段和最小值问题例１０㊀如图１９ꎬ已知直线ａʊｂꎬ直线ａ和直线ｂ之间距离为ｃꎬ在直线ａ和直线ｂ上分别找点Ａ㊁Ｂ两点ꎬ使ＡＢʅａꎬ且ＭＡ＋ＡＢ＋ＢＮ的值最小.解析㊀如图２０ꎬ将点Ｍ向下平移ｃ个单位到Ｍᶄꎬ连接ＭᶄＮ交直线ｂ于点Ｂꎬ过点Ｂ作ＢＡʅｌ１于点Ａꎬ点Ａ㊁Ｂ两点是所找的点.图１９㊀例１０题图㊀㊀㊀㊀㊀图２０㊀例１０解析图３.２同侧线段和的最小值问题例１１㊀如图２１ꎬ在直线ａ上找Ａ㊁Ｂ两点(Ａ在Ｂ左侧)ꎬ使得ＡＢ＝ｋꎬ且ＭＡ＋ＡＢ＋ＢＮ的值最小.解析㊀如图２２ꎬ将点Ｍ向右平移ｋ个单位到点Ｍᶄꎬ作点Ｍᶄ关于直线ａ的对称点Ｍᵡꎬ连接ＭᵡＮ交直线ａ于点Ｂꎬ将点Ｂ向左平移ｋ个单位到点ＡꎬＡ㊁Ｂ两点是所找的点.图２１㊀例１１题图㊀㊀㊀㊀㊀㊀图２２㊀例１１解析图４结束语在初中数学教学中ꎬ教师引导学生经历并弄清 一线两点 型㊁ 一定两线 型㊁ 一定长ꎬ两定点 型最值问题的求解方法ꎬ不仅能够提高学生分析问题和解决问题的能力ꎬ而且能够使教师的教学效果达到 教是为了不教 之目的[２].参考文献:[１]孔令志ꎬ马学斌.２０２０年中考数学压轴题高频热点问题赏析(４)线段和的最小值问题:两点之间线段最短[Ｊ].中小学数学(初中版)ꎬ２０２０(１２):３７－４０.[２]叶婷婷.初中几何 线段最值 问题的求解策略[Ｊ].启迪与智慧(上)ꎬ２０２０(４):９６.[责任编辑:李㊀璟]５１。

两点之间线段最短教学目标：理解“两点之间，线段最短”的结论，并能用这一结论解释一些简单的问题。

重点：结论的应用过程和拓展问题的探究过程难点：拓展问题的探究过程教学过程设计热身准备：我想试试罗赛蒂那个说“我想试试”的小孩他将登上山巅，那个说“我不成”的小孩，在山下停步不前。

“我想试试”每天办成很多事，“我不成”就真一事无成。

因此你务必说“我想试试”，将“我不成”弃于埃尘。

二、新课教学绿地里本没有路，走的人多了……你能解释一下原因？2、数学活动：在纸上任意点两点，用线联接它们，量一下它们的长短，比较一下谁最短？得出结论2、解释、应用与交流问题1、怎样走最近？如图1，从A地到B地有四条道路，除它们外能否再修一条从A地到B地的最短道路？问题2、河道长度如图2，把原来弯曲的河道改直，A、B两地间的河道长度有什么变化？图2问题3、九曲桥（2）如图3，公园里设计了曲折迂回的桥，这样做对游人观赏湖面风光有什么影响？与修一座笔直的桥相比，这样做是否增加了游人在桥上行走的路程？说出其中的道理。

图3你还能举出一些类似的例子吗？小猫看见鱼，小狗看见骨头后会怎样运动？有人过马路到对面的商店去，但没有走人行道，为什么呢？3、拓广探索与交流蚂蚁爬行路线最短问题。

如图4，一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B，怎样爬行路线最短？如果要爬行到顶点C呢？图4利用手中的正方体具体实验一下，告诉大家你的结论。

三、回顾、思考与交流设想自己是一名园林设计师或者是一名管理者，在进行公共绿地设计时对情境一的一些思考与探讨能给你一些什么启发。

四、作业对蚂蚁爬行最短问题的再思考：如果蚂蚁在长方体的一个顶点上，如果蚂蚁在圆柱上，这时问题发生怎样的变化？问题如何解？请把你对此问题的研究写成数学小作文，注意写出自己的情感体验《关于最短路径思考》已经学过“两点之间，线段最短”这个数学公理了。

这看似简单的八个字蕴涵着许多奥妙，将它扩展、延伸可得到一个最短路径问题、即求连接A、B两点的线段中哪一条最短。

A B C第5题图生活中的线段应用两点之间，线段最短是线段的基本的性质，它在生活中有着广泛的应用．例1、如图，A 、B 是两个车站，若要在公路l 上修建一个加油站，如何使它到车站A 、B 的距离和最小，请在公路l 上标出点P 的位置，并说明理由．分析：根据连接两点的线中，线段最短，只需在A 、B 间作一条线段与直线l 的相交，交点就是到A 、B 两点距离和最小的点．解：连接A 、B ，与l 交于点P ，即为所建加油站的位置，因为两点之间线段最短．例2、在同一个学校上学的小明、小伟、小红三位同学住在A 、B 、C 三个住宅区，如图2所示，A 、B 、C 三点共线，且AB ＝60米，BC ＝100米，他们打算合租一辆接送车去上学，由于车位紧张，准备在此之间只设一个停靠点，为使三位同学步行到停靠点的路程之和最小，你认为停靠点应该设在______．分析：本题是在线段AC 上找一点P ，使总路程S=AP+BP+CP 最小．可分点P 在AB 间、BC 间和P 与B 重合三种情况分类计算S ，再进行比较，找出符合要求的点。

解：设停靠点应该建在P 点处，设PB=x 米，则当P 点在AB 间时，S=AP+BP+CP=（60-x ）+x+（100+x ）=（160+x ）；当P 点在BC 间时，S=AP+BP+CP=（60+x ）+x+（100-x ）=（160+x ）；当P 点与B 点重合时，S=AP+BP+CP=60+0+100=160。

综合上述，停靠点设在B 点时，S 最小，并且是固定值160米． 说明：本题把实际问题转化为几何问题，然后根据所学的几何知识进行解决．例3、先阅读下面的材料，然后解答问题： 在一条直线上有依次排列的n （n ＞1）台机床在工作，我们要设置零件供应站P ，使这n 台机床到供应站P 的距离总和最小，要解决这个问题，先退到比较简单的情形：如果直线上有2台机床A1、A2时，很明显供应站P 设在A1和A2之间的任何地方都行，因为甲和乙走的距离之和等于A1到A2的距离．如果直线上有3台机床A1、A2、A3时，不难判断，供应站P 设在中间一台机床A2处最合适，因为如果设在A2处，甲、乙和丙所走的距离之和恰好为A1到A3的距离，若把设到别处，那么甲和丙所走的距离之和仍是A1到A3的距离，可是乙还得走从A2到P 这多出来的一段，故供应站P 设在A2处是最佳选择．不难知道，如果直线上有4台机床，P 应设在第2台与第3台之间的任何地方；有5台机床，P 应设在第3台的位置．提出问题：如果有n 台机床时，供应站P 应设在何处？分析：本题要求我们通过阅读理解，提炼出题目中隐含的规律，再用规律来解题．阅读本题可得出，当机床台数为偶数时，点P 应在最中间两点之间的任何地方；当机床台数为奇数时，供应站P 应与最中间的那一台机床的位置重合．解：当n 为偶数时，供应站P 应设在第12n 台和（12n +1）台之间的任何地方；当n 为奇数时，供应站p 应设在第1(1)2n 台的位置．。

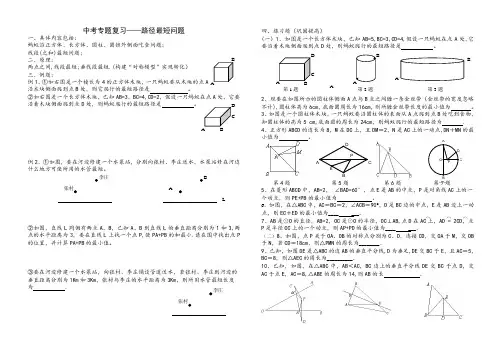
A B C DA B C DABABL图(2)EBDA CP图(3)DO CP中考专题复习——路径最短问题一、具体内容包括：蚂蚁沿正方体、长方体、圆柱、圆锥外侧面吃食问题；线段(之和)最短问题；二、原理：两点之间,线段最短;垂线段最短.(构建“对称模型”实现转化）三、例题：例1、①如右图是一个棱长为4的正方体木块，一只蚂蚁要从木块的点A沿木块侧面爬到点B处，则它爬行的最短路径是。

②如右图是一个长方体木块，已知AB=3，BC=4,CD=2，假设一只蚂蚁在点A处，它要沿着木块侧面爬到点D处，则蚂蚁爬行的最短路径是。

例2、①如图，要在河边修建一个水泵站，分别向张村、李庄送水，水泵站修在河边什么地方可使所用的水管最短。

②如图，直线L同侧有两点A、B，已知A、B到直线L的垂直距离分别为1和3,两点的水平距离为3，要在直线L上找一个点P,使PA+PB的和最小.请在图中找出点P 的位置，并计算PA+PB的最小值。

③要在河边修建一个水泵站，向张村、李庄铺设管道送水，若张村、李庄到河边的垂直距离分别为1Km和3Km，张村与李庄的水平距离为3Km，则所用水管最短长度为 . 四、练习题（巩固提高）(一）1、如图是一个长方体木块，已知AB=5,BC=3,CD=4,假设一只蚂蚁在点A处,它要沿着木块侧面爬到点D处，则蚂蚁爬行的最短路径是。

2、现要在如图所示的圆柱体侧面A点与B点之间缠一条金丝带（金丝带的宽度忽略不计),圆柱体高为6cm，底面圆周长为16cm，则所缠金丝带长度的最小值为。

3、如图是一个圆柱体木块，一只蚂蚁要沿圆柱体的表面从A点爬到点B处吃到食物，知圆柱体的高为5 cm,底面圆的周长为24cm，则蚂蚁爬行的最短路径为 .4、正方形ABCD的边长为8，M在DC上，且DM＝2，N是AC上的一动点,DN＋MN的最小值为。

第4题第5题第6题第7题5、在菱形ABCD中，AB=2，∠BAD=60°，点E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值为。

初中数学[最短路径问题]典型题型及解题技巧最短路径问题中,关键在于，我们善于作定点关于动点所在直线的对称点，或利用平移和展开图来处理。

这对于我们解决此类问题有事半功倍的作用。

理论依据：“两点之间线段最短”，“垂线段最短”，“点关于线对称”，“线段的平移”“立体图形展开图”。

教材中的例题“饮马问题”，“造桥选址问题”“立体展开图”。

考的较多的还是“饮马问题”。

知识点：“两点之间线段最短”，“垂线段最短”，“点关于线对称”，“线段的平移”。

“饮马问题”，“造桥选址问题”。

考的较多的还是“饮马问题”，出题背景变式有角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。

解题总思路：找点关于线的对称点实现“折”转“直”，近两年出现“三折线”转“直”等变式问题考查。

一、两点在一条直线异侧例：已知：如图，A，B在直线L的两侧，在L上求一点P，使得PA+PB最小。

解：连接AB,线段AB及直线L的交点P ，就是所求。

（根据：两点之间线段最短.）二、两点在一条直线同侧例：图所示，要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A、B到它的距离之和最短．解：只有A、C、B在一直线上时，才能使AC+BC最小．作点A关于直线“街道”的对称点A′，然后连接A′B，交“街道”于点C，则点C就是所求的点．三、一点在两相交直线内部例：已知：如图A是锐角∠MON内部任意一点，在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小.解：分别作点A关于OM，ON的对称点A′，A″；连接A′，A″，分别交OM，ON于点B、点C，则点B、点C即为所求分析：当AB 、BC 和AC 三条边的长度恰好能够体现在一条直线上时，三角形的周长最小例：如图，A.B 两地在一条河的两岸，现要在河上建一座桥MN ，桥造在何处才能使从A 到B 的路径AMNB 最短？（假设河的两岸是平行的直线，桥要及河垂直）解：1.将点B 沿垂直及河岸的方向平移一个河宽到E ，2.连接AE 交河对岸及点M,则点M 为建桥的位置，MN 为所建的桥。

最短路线一在学习几何知识时，同学们已经学过如下两个结论：（1）连结两点的所有线中，直线段是最短的；（2）直线外的一个定点与直线上的各点的连线以垂线为最短．利用这两个结论可以解决许多实际生活中求最短路线的问题．例1甲、乙两村之间隔一条河，如图13—1．现在要在小河上架一座桥，使得这两村之间的行程最短，桥应修在何处？分析：设甲、乙两村分别用点A、B表示．要在河上架桥，关键是要选取一个最佳建桥的位置，使得从甲村出发经过桥到乙村的路程最短．即从甲村到甲村河边的桥头的距离加上桥长（相当于河的宽度），再加上乙村到乙村河边的桥头的距离尽可能短，这是一个求最短折线的问题．直接找出这条折线很困难，能否可以把它转化为直线问题呢？由于河的宽度不变，不论桥修在哪里，桥都是必经之路，且桥长相当于河宽，是一个定值，所以可以预先把这段距离扣除，只要使两镇到河边桥头的距离最短就可以了．所谓预先将桥长扣除，就是假设先走完桥长，即先把桥平移到甲村，先过了桥，到C 点，如图13—2，找出C到B的最短路线，实际上求最短折线问题转化为直线问题．解：如图13—2．过A点作河岸的垂线，在垂线上截取AC的长等于河宽．连BC交与乙村的河岸于F点，作EF垂直于河的另一岸于E点，则EF为架桥的位置，也就是AE+EF+FB 是两村的最短路线．例2如图13—3，A、B两个学校都在公路的同侧．想在这两校的附近的公路上建一个汽车站，要求车站到两个学校的距离之和最小，应该把车站建在哪里？分析：车站建在哪里，使得A到车站与B到车站的距离之和最小，仍然是求最短折线问题，同例1一样关键在于转化成直线问题就好办了．采用轴对称（直线对称）作法．解：作点B关于公路（将公路看作是一条直线）的对称点B′，如图13—4，即过B点作公路（直线）的垂线交直线于O，并延长BO到B′，使BO=OB′．连结AB′交直线于点E，连BE，则车站应建在E处，并且折线AEB为最短．为什么这条折线是最短的呢？分两步说明：（1）因为B与B′关于直线对称，根据对称点的性质知，对称轴上的点到两个对称点的距离相等，有BE=B′E，所以AB′=AE+EB′=AE+EB（2）设E′是直线上不同于E的任意一点，如图13—5，连结AE′、E′B、E′B′，可得AE′+E′B=AE′+E′B′＞AB′（两点之间线段最短）上式说明，如果在E点以外的任意一点建车站，所行的路程都大于折线AEB．所以折线AEB最短．例3如图13—6，河流EF与公路FD所夹的角是一个锐角，某公司A在锐角EFD内．现在要在河边建一个码头，在公路边修建一个仓库，工人们从公司出发，先到河边的码头卸货，再把货物转运到公路边的仓库里去，然后返回到A处，问仓库、码头各应建在何处，使工人们所行的路程最短．分析：工人们从A出发先到河边码头，再到公路的仓库，然后回到A处，恰好走一个三角形，现在要求三角形的另外两个顶点分别建在河岸与公路的什么位置能使这个三角形的三边之和为最小，利用轴对称原理作图．解：过A分别作河岸、公路的对称点A′、A″，如图13—7，连结A′A″，交河岸于M，交公路于N，则三角形AMN各边之和等于直线A′A″的长度，所以仓库建在N处，码头建在M处，使工人们所行的路程最短．例4如图13—8是一个长、宽、高分别为4分米、2分米、1分米的长方体纸盒．一只蚂蚁要从A点出发在纸盒表面上爬到B点运送食物，求蚂蚁行走的最短路程．分析：因为是在长方体的表面爬行，求的是立体图形上的最短路线问题，往往可以转化为平面上的最短路线问题．将蚂蚁爬行经过的两个面展开在同一平面上，如图13—9，在展开图中，AB间的最短路线是连结这两点的直线段，但要注意，蚂蚁可沿几条路线到达B点，需对它们进行比较．解：蚂蚁从A点出发，到B点，有三条路线可以选择：（1）从A点出发，经过上底面然后进入前侧面到达B点，将这两个平面展开在同一平面上，这时A、B间的最短路线就是连线AB，如图13—9（1），AB是直角三角形ABC 的斜边，根据勾股定理，AB2=AC2+BC2=（1+2）2+42=25（2）从A点出发，经过左侧面，然后进入前侧面到达B点，将这两个面展开在同一平面上，如图13—9（2），同理AB2=22+（1+4）2=29（3）从A点出发，经过上底面，然后进入右侧面到达B点，将这两个面展开在同一平面上，如图13—9（3），得AB2=（2+4）2+12=37比较这三条路线，25最小，所以蚂蚁按图13—9（1）爬行的路线最短，最短路程为5分米．例5如图13—10，在圆柱形的木桶外，有一个小甲虫要从桶外的A点爬到桶内的B点．已知A点到桶口C点的距离为14厘米，B点到桶口D点的距离是10厘米，而C、D两点之间的弧长是7厘米．如果小甲虫爬行的是最短路线，应该怎么走？路程是多少？分析：先设想将木桶的圆柱展开成矩形平面，如图13—11，由于B点在桶内，不便于作图，利用轴对称原理，作点B关于直线CD的对称点B′，这就可以用B′代替B，从而找出最短路线．解：如图13—11，将圆柱体侧面展成平面图形．作点B关于直线CD的对称点B′，连结AB′，AB′是A、B′两点间的最短距离，与桶口边交于O点，则OB′=OB，AB′=AO+OB，那么A、B之间的最短距离就是AO+OB，所以小甲虫在桶外爬到O点后，再向桶内的B点爬去，这就是小甲虫爬行的最短路线．延长AC到E，使CE＝B′D，因为△AEB′是直角三角形，AB′是斜边，EB′=CD=7厘米，AE=14+10=24（厘米），根据勾股定理：AB′2=AE2+EB′2=242+72=625所以AB′=25（厘米）即小甲虫爬行的最短路程是25厘米．。

【基本问题 】【问题 1】 作法 图形 原理两点之间线段最短．连 AB ，与 l 交点即为P ．PA+PB 最小值为 AB ．在直线 l 上求一点 P ，使 PA+PB 值最小．【问题 2】“将军饮马” 作法 图形 原理作 B 对于 l 的对称点 B ＇两点之间线段最短． 连 A B ＇，与 l 交点即为 P ．PA+PB 最小值为 A B ＇．在直线 l 上求一点 P ，使 PA+PB 值最小．【问题 3】 作法 图形 原理分别作点 P 对于两直线的两点之间线段最短． 对称点 P ＇和 P ＇，连 P ＇P ＇， PM +MN +PN 的最小值为 与两直线交点即为 M ， N ．线段 P ＇P ＇＇的长．在直线 l 1 、 l 2 上分别求点 M 、 N ，使△ PMN 的周长 最小．【问题 4】 作法 图形 原理分别作点 Q 、P 对于直线 两点之间线段最短．l 1 、 l 2 的对称点 Q ＇和 P ＇四边形 PQMN 周长的最小连 Q ＇P ＇，与两直线交点即值为线段 P ＇P ＇＇的长．在直线 l 1 、 l 2 上分别求点 为 M ， N ．M 、 N ，使四边形 PQMN 的周长最小．【问题 5】“造桥选址” 作法 图形 原理将点 A 向下平移 MN 的长两点之间线段最短．度单位得 A ＇，连 A ＇B ，交 nAM +MN +BN 的最小值为于点 N ，过 N 作 NM ⊥ m 于直线 m ∥ n ，在 m 、 n ，A ＇B+MN ．上分别求点 M ．M 、N ，使 MN⊥ m ，且 AM+ MN+ BN 的值最小．【问题 6】 作法图形 原理将点 A 向右平移 a 个长度两点之间线段最短．- 1 -单位得 A＇，作 A ＇对于 l 的AM +MN +BN 的最小值为对称点 A＇，连 A＇B，交直线A＇B+ MN．l 于点 N，将 N 点向左平在直线 l 上求两点 M 、N（ M移 a 个单位得M．在左），使 MN a ，并使AM + MN+ NB 的值最小．【问题 7】作法图形原理作点 P 对于 l 1的对称点点到直线，垂线段最短．P ＇，作 P＇B⊥ l 2于 B，交 l 2PA+ AB 的最小值为线段P＇于 A．B的长．在 l 1上求点 A，在 l 2上求点 B，使 PA+ AB 值最小．【问题 8】作法图形原理作点 A 对于 l 2的对称点两点之间线段最短．A ＇，作点B 对于 l1的对称A 为 l 1上必定点， B 为 l 2上AM +MN +NB 的最小值为点 B＇，连 A＇B＇交l 2于 M，必定点，在 l 2上求点 M ，交 l 1于 N．线段 A＇B＇的长．在l 1上求点N ，使AM + MN+ NB 的值最小．【问题 9】作法图形原理垂直均分上的点到线段两连 AB ，作 AB 的中垂线与端点的距离相等．直线 l 的交点即为P．PA PB ＝0．在直线l 上求一点P，使PA PB 的值最小．【问题 10】作法图形原理三角形随意两边之差小于作 B 对于 l 的对称点B＇作直线 A B＇，与 l 交点即为 P．在直线l 上求一点P，使第三边．PA PB ≤AB＇．PA PB 最大值＝AB＇．PA PB 的值最大．【精选练习】1．如下图，正方形ABCD 的面积为12，△ ABE 是等边三角形，点 E 在正方形ABCD 内，在对角线AC- 2 -上有一点 P，使 PD+PE 的和最小，则这个最小值为（）A ．23B．26C．3 D ．62．如图，在边长为 2 的菱形 ABCD 中，∠ ABC＝ 60°，若将△ACD 绕点 A 旋转，当AC′、 AD ′分别与 BC、CD 交于点 E、 F ，则△ CEF 的周长的最小值为（）A ．2B ． 2 3C． 23 D ． 43．四边形ABCD 中，∠ B＝∠ D＝ 90°，∠ C＝ 70°，在 BC、 CD 上分别找一点M、 N，使△ AMN 的周长最小时，∠ AMN +∠ ANM 的度数为（）A ．120°B ．130°C． 110°D． 140°4．如图，在锐角△ABC 中， AB＝ 4 2 ，∠BAC＝45°，∠BAC的均分线交BC 于点 D ， M、N 分别是 AD 和 AB 上的动点，则BM +MN 的最小值是．5．如图， Rt△ ABC 中，∠ C＝ 90°，∠ B＝ 30°， AB＝ 6，点 E 在 AB 边上，点 D 在 BC 边上（不与点B、 C 重合），且 ED ＝ AE，则线段 AE 的取值范围是．6．如图，∠ AOB＝ 30°，点 M、 N 分别在边OA、OB 上，且 OM ＝ 1，ON＝ 3，点 P、Q 分别在边 OB、OA上，则 MP＋ PQ＋ QN 的最小值是 _________．7．如图，三角形△ABC中，∠ OAB＝∠ AOB＝15°，点B在x轴的正半轴，坐标为B( 6 3 ， 0)．OC 均分∠ AOB，点 M 在 OC 的延伸线上，点N 为边 OA 上的点，则MA＋ MN 的最小值是 ______．- 3 -8．已知 A（ 2，4）、B（ 4，2）．C 在 y 轴上， D 在 x 轴上，则四边形 ABCD 的周长最小值为，此时C、 D 两点的坐标分别为．9．已知 A（ 1， 1）、 B（ 4， 2）．（ 1） P 为 x 轴上一动点，求PA+PB 的最小值和此时P 点的坐标；（ 2） P 为 x 轴上一动点，求PA PB 的值最大时P 点的坐标；（ 3） CD 为 x 轴上一条动线段， D 在 C 点右侧且 CD ＝ 1，求当 AC+CD +DB 的最小值和此时 C 点的坐标；10．点 C 为∠ AOB 内一点．（ 1）在 OA 求作点 D， OB 上求作点E，使△ CDE 的周长最小，请画出图形；（ 2）在（ 1）的条件下，若∠AOB＝ 30°， OC＝10，求△ CDE 周长的最小值和此时∠DCE 的度数．- 4 -。