迈达斯之——静力弹塑性分析基本原理及方法

静力弹塑性分析(Pushover 分析)■ 简介Pushover 分析是考虑构件的材料非线性特点，分析构件进入弹塑性状态直至到达极限状态时结构响应的方法。

Pushover 分析是最近在地震研究及耐震设计中经常采用的基于性能的耐震设计(Performance-Based Seismic Design, PBSD)方法中最具代表性的分析方法。

所谓基于性能的耐震设计就是由用户及设计人员设定结构的目标性能(target performance)，并使结构设计能满足该目标性能的方法。

Pushover 分析前要经过一般设计方法先进行耐震设计使结构满足小震不坏、中震可修的规范要求，然后再通过pushover 分析评价结构在大震作用下是否能满足预先设定的目标性能。

计算等效地震静力荷载一般采用如图2.24所示的方法。

该方法是通过反应修正系数(R)将设计荷载降低并使结构能承受该荷载的方法。

在这里使用反应修正系数的原因是为了考虑结构进入弹塑性阶段时吸收地震能量的能力，即考虑结构具有的延性使结构超过弹性极限后还可以承受较大的塑性变形，所以设计时的地震作用就可以比对应的弹性结构折减很多，设计将会更经济。

目前我国的抗震规范中的反应谱分析方法中的小震影响系数曲线就是反应了这种设计思想。

这样的设计方法可以说是基于荷载的设计(force-based design)方法。

一般来说结构刚度越大采用的修正系数R 越大，一般在1~10之间。

但是这种基于荷载与抗力的比较进行的设计无法预测结构实际的地震响应，也无法从各构件的抗力推测出整体结构的耐震能力，设计人员在设计完成后对结构的耐震性能的把握也是模糊的。

基于性能的耐震设计中可由开发商或设计人员预先设定目标性能，即在预想的地震作用下事先设定结构的破坏程度或者耗能能力，并使结构设计满足该性能目标。

结构的耗能能力与结构的变形能力相关，所以要预测到结构的变形发展情况。

所以基于性能的耐震设计经常通过评价结构的变形来实现，所以也可称为基于位移的设计(displacement-based design)。

基于Midas的复杂空间结构静力弹塑性分析I. 前言-理论基础介绍-II. 分析方法-定义复杂空间结构静力弹塑性分析-Midas的基本原理和算法-III. 计算和分析-分析和计算的主要步骤-确保比较结果的准确性和稳定性-IV. 结果和讨论-分析和计算的结果-结果的解读和分析-讨论结果与预期的相似点和不同点-V.结论和未来工作-总结分析和计算的工作和结果-未来研究和应用的建议-结束语第一章：前言随着人们对建筑物安全性和可靠性的更高要求，复杂的空间结构的设计和分析变得越来越重要。

在这个背景下，静力弹塑性分析作为一种广泛应用的分析方法，在工程实践中被广泛采用。

本论文的目的是基于Midas软件平台对复杂空间结构进行静力弹塑性分析。

本文将介绍分析方法、Midas算法、计算和分析过程，结果和讨论。

最后，我们将提出一些对于未来工作的建议。

第二章：分析方法复杂空间结构静力弹塑性分析是一种能够模拟结构变形和各种应力作用的分析方法。

该方法通过确定结构的应力分布和形变，确定结构在预定载荷作用下的变形模式和承载能力。

在处理复杂的空间结构设计和分析时，静力弹塑性分析是一种理论和实践有效的工具。

Midas软件是一种用于计算结构应力分布和形变的数值方法。

它可以模拟各种静态和动态载荷下的结构变形和应力分布，同时还可以确定最大承载能力。

Midas算法采用了高级的非线性有限元分析模型，以优化可靠性和精确度。

它还采用了可视化分析工具，帮助用户进行更有效的分析和设计。

第三章：计算和分析在进行复杂空间结构静力弹塑性分析时，需要进行以下几个步骤：1. 建模和定义材料特性2. 定义结构荷载和支持条件3. 进行静力计算并确定初始应力和应变4. 进行弹性分析5. 进行塑性分析6. 进行后处理和结果分析在Midas软件中，用户可以方便地进行这些步骤，从而得到完整的静力弹塑性分析结果。

首先，用户需要通过建模和定义材料特性来创建一个准确的模型。

该模型需要包括材料物理性质、外部荷载和支持条件信息。

浅谈静力弹塑性分析（Pushover ）的理解与应用摘要：本文首先介绍采用静力弹塑性分析（Pushover ）的主要理论基础和分析方法，以Midas/Gen 程序为例，采用计算实例进行具体说明弹塑性分析的步骤和过程，表明Pushover 是罕遇地震作用下结构分析的有效方法。

关键词：静力弹塑性 Pushover Midas/Gen 能力谱 需求谱 性能点一、基本理论静力弹塑性分析方法，也称Pushover 分析法，是基于性能评估现有结构和设计新结构的一种静力分析方法，在一定精度范围内对结构在罕遇地震作用下进行弹塑性变形分析。

简要地说，在结构计算模型上施加按某种规则分布的水平侧向力或侧向位移，单调加荷载（或位移）并逐级加大；一旦有构件开裂（或屈服）即修改其刚度（或使其退出工作），进而修改结构总刚度矩阵，进行下一步计算，依次循环直到控制点达到目标位移或建筑物倾覆为止，得到结构能力曲线，之后对照确定条件下的需求谱，并判断是否出现性能点，从而评价结构是否能满足目标性能要求。

Pushover 分析的基本要素是能力谱曲线和需求谱曲线，将两条曲线放在同一张图上，得出交会点的位移值，同位移容许值比较，检验是否满足特定地震作用下的弹塑性变形要求。

能力谱曲线由能力曲线（基底剪力-顶点位移曲线）转化而来（图1）。

与地震作用相应的结构基底剪力与结构加速度为正相关关系，顶点位移与谱位移为正相关关系，两种曲线形状一致。

其对应关系为：1/αG V S a =roofroof d X S ,11γ∆=，图1 基底剪力-顶点位移曲线转换为能力谱曲线其中1α、1γ、roof X ,1分别为第一阵型的质量系数，参与系数、顶点位移。

该曲线与主要建筑材料的本构关系曲线具有相似性，其实其物理意义亦有对应，在初始阶段作用力与变形为线性关系，随着作用力的增大，逐渐进入弹塑性阶段，变形显著增长，不论对于构件，还是结构整体，都是这个规律。

需求谱曲线由标准的加速度响应谱曲线转化而来。

m i d a s C i v i lm i d a s C i v i lm i d a s C i v i l图2.8.38 基于位移设计法的结构抗震性能评价m i d a s C i v i l示。

m i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i l1n λ- : 前一步骤(n-1)的荷载因子1λ : 第1荷载步的荷载因子nstep : 总步骤数i : 等差增量步骤号当前步骤的外力向量如下。

0n n λ=⋅P P(10)(3) 第3阶段: 最终步骤的荷载增量(n nstep =) 最终荷载步骤(nstep )的外力向量如下、0nstep nstep λ=⋅P P ; 1.0nstep λ= (11)图2.8.43 自动调整荷载步长的例题(荷载因子结果)m i d a s C i v i l2. 点击步长控制选项 > 增量控制函数定义步长控制函数m i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lATC-40中对不同结构响应类型规定了谱折减系数的下限值(参见表2.8.7)。

■ 简介Pushover 分析是考虑构件的材料非线性特点，分析构件进入弹塑性状态直至到达极限状态时结构响应的方法。

Pushover 分析是最近在地震研究及耐震设计中经常采用的基于性能的耐震设计(Performance-Based Seismic Design, PBSD)方法中最具代表性的分析方法。

所谓基于性能的耐震设计就是由用户及设计人员设定结构的目标性能(target performance)，并使结构设计能满足该目标性能的方法。

Pushover 分析前要经过一般设计方法先进行耐震设计使结构满足小震不坏、中震可修的规范要求，然后再通过pushover 分析评价结构在大震作用下是否能满足预先设定的目标性能。

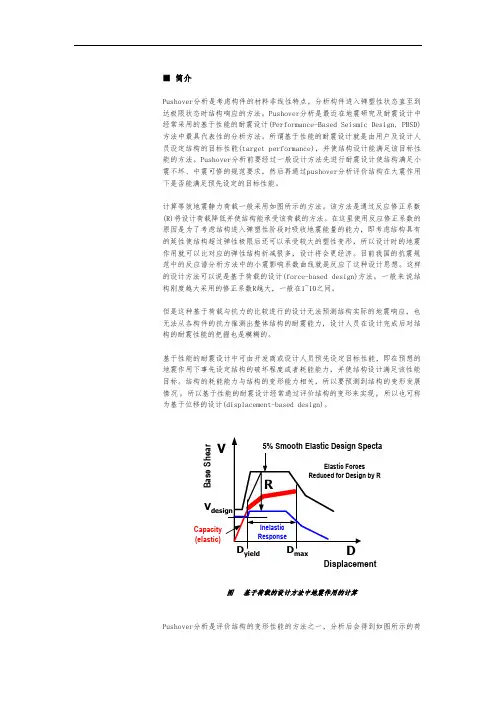
计算等效地震静力荷载一般采用如图所示的方法。

该方法是通过反应修正系数(R)将设计荷载降低并使结构能承受该荷载的方法。

在这里使用反应修正系数的原因是为了考虑结构进入弹塑性阶段时吸收地震能量的能力，即考虑结构具有的延性使结构超过弹性极限后还可以承受较大的塑性变形，所以设计时的地震作用就可以比对应的弹性结构折减很多，设计将会更经济。

目前我国的抗震规范中的反应谱分析方法中的小震影响系数曲线就是反应了这种设计思想。

这样的设计方法可以说是基于荷载的设计(force-based design)方法。

一般来说结构刚度越大采用的修正系数R 越大，一般在1~10之间。

但是这种基于荷载与抗力的比较进行的设计无法预测结构实际的地震响应，也无法从各构件的抗力推测出整体结构的耐震能力，设计人员在设计完成后对结构的耐震性能的把握也是模糊的。

基于性能的耐震设计中可由开发商或设计人员预先设定目标性能，即在预想的地震作用下事先设定结构的破坏程度或者耗能能力，并使结构设计满足该性能目标。

结构的耗能能力与结构的变形能力相关，所以要预测到结构的变形发展情况。

所以基于性能的耐震设计经常通过评价结构的变形来实现，所以也可称为基于位移的设计(displacement-based design)。

收稿日期:2003-02-16;　修订日期:2003-05-12 基金项目:华东建筑设计研究院有限公司第2001年度科研项目. 作者简介:汪大绥(1941-),男,江西乐平人,教授级高工,主要从事大型复杂结构设计与研究工作.文章编号:100726069(2004)0120045209静力弹塑性分析(Pushover Analysis )的基本原理和计算实例汪大绥　贺军利　张凤新(华东建筑设计研究院有限公司,上海200002)摘要:阐述了美国两本手册FE M A273/274和AT C -40中关于静力弹塑性分析的基本原理和方法,给出了利用ET ABS 程序进行适合我国地震烈度分析的计算步骤,并用一框剪结构示例予以说明,表明Pushover 方法是目前对结构进行在罕遇地震作用下弹塑性分析的有效方法。

关键词:静力弹塑性;能力谱;需求谱;性能点中图分类号:P315.6 文献标识码:AThe basic principle and a case study of the static elastoplastic analysis (pushover analysis)W ANG Da 2sui HE Jun 2li ZH ANG Feng 2xin(East China Architectural Design &Research Institute C o.,Ltd ,Shanghai 200002,China )Abstract :This paper reviews the basic principles and methods of the static elasto 2plastic analysis (pushover analysis )in FE M A273/274and in ATC 240.Its main calculation procedures are summarized and a case study is presented for the frame 2shearwall structure designed according to China C ode for Seismic Design by means of ET ABS.It has been proved that pushover analysis is a effective method of structural elastoplastic analysis under the maximum earthquake action.K ey w ords :static elastoplastic ;capacity spectrum ;demand spectrum ;performance point1　前言利用静力弹塑性分析(Pushover Analysis )进行结构分析的优点在于:既能对结构在多遇地震下的弹性设计进行校核,也能够确定结构在罕遇地震下潜在的破坏机制,找到最先破坏的薄弱环节,从而使设计者仅对局部薄弱环节进行修复和加强,不改变整体结构的性能,就能使整体结构达到预定的使用功能;而利用传统的弹性分析,对不能满足使用要求的结构,可能采取增加新的构件或增大原来构件的截面尺寸的办法,结果是增加了结构刚度,造成了一定程度的浪费,也可能存在新的薄弱环节和隐患。

结构静力弹塑性分析的原理和计算实例一、本文概述结构静力弹塑性分析是一种重要的工程分析方法，用于评估结构在静力作用下的弹塑性行为。

该方法结合了弹性力学、塑性力学和有限元分析技术，能够有效地预测结构在静力加载过程中的变形、应力分布以及破坏模式。

本文将对结构静力弹塑性分析的基本原理进行详细介绍，并通过计算实例来展示其在实际工程中的应用。

通过本文的阅读，读者可以深入了解结构静力弹塑性分析的基本概念、分析流程和方法，掌握其在工程实践中的应用技巧，为解决实际工程问题提供有力支持。

二、弹塑性理论基础弹塑性分析是结构力学的一个重要分支，它主要关注材料在受力过程中同时发生弹性变形和塑性变形的情况。

在弹塑性分析中，材料的应力-应变关系不再是线性的，而是呈现出非线性特性。

当材料受到的应力超过其弹性极限时，材料将发生塑性变形，这种变形在卸载后不能完全恢复，从而导致结构的永久变形。

弹塑性分析的理论基础主要包括塑性力学、塑性理论和弹塑性本构关系。

塑性力学主要研究塑性变形的产生、发展和终止的规律，它涉及到塑性流动、塑性硬化和塑性屈服等概念。

塑性理论则通过引入屈服函数、硬化法则和流动法则等，描述了材料在塑性变形过程中的应力-应变关系。

弹塑性本构关系则综合考虑了材料的弹性和塑性变形行为，建立了应力、应变和应变率之间的关系。

在结构静力弹塑性分析中，通常需要先确定材料的弹塑性本构模型，然后结合结构的边界条件和受力情况，建立结构的弹塑性平衡方程。

通过求解这个平衡方程，可以得到结构在静力作用下的弹塑性变形和应力分布。

弹塑性分析在结构工程中有着广泛的应用，特别是在评估结构的承载能力、变形性能和抗震性能等方面。

通过弹塑性分析，可以更加准确地预测结构在极端荷载作用下的响应，为结构设计和加固提供科学依据。

以上即为弹塑性理论基础的主要内容，它为我们提供了分析结构在弹塑性阶段行为的理论框架和工具。

在接下来的计算实例中，我们将具体展示如何应用这些理论和方法进行结构静力弹塑性分析。

例题钢筋混凝土静力弹塑性推覆分析2 例题. 钢筋混凝土静力弹塑性推覆分析概要此例题介绍使用midas Gen 的反应谱分析功能来进行钢筋混凝土结构分析的方法。

此例题的步骤如下:1.简介2.设定操作环境及设定材料截面3.用建模助手建立模型4.建立框架柱及剪力墙5.楼层复制及生成层数据文件6.定义边界条件7.输入楼面及梁单元荷载8.输入风荷载9.定义质量10.运行分析11.荷载组合12.一般设计参数13.钢筋混凝土构件设计参数14.钢筋混凝土构件设计15.静力弹塑性分析例题 钢筋混凝土静力弹塑性推覆分析31.简介本例题介绍使用midas Gen 的静力弹塑性分析功能来进行抗震设计的方法。

例题模型为九层钢筋混凝土框-剪结构。

(该例题数据仅供参考) 基本数据如下： 轴网尺寸：见平面图柱: 500mmx500mm 主梁： 250mmx600 mm 混凝土： C30 剪力墙： 250mm图2 分析模型例题钢筋混凝土静力弹塑性推覆分析4 2.设定操作环境及定义材料和截面1.主菜单选择文件>新项目文件>保存：输入文件名并保存2.主菜单选择工具>设置>单位系:长度 m, 力 kN图3 定义单位体系3.主菜单选择特性>材料>材料特性值：添加：定义C30混凝土材料号：1 数据库：C30 规范：GB10(RC)例题 钢筋混凝土静力弹塑性推覆分析5图4 定义材料4.主菜单选择 特性>截面>截面特性值：添加：定义梁、柱截面尺寸例题钢筋混凝土静力弹塑性推覆分析6图5 定义梁、柱截面5.主菜单选择特性>截面>厚度：添加：定义剪力墙厚度图6 定义剪力墙厚度例题 钢筋混凝土静力弹塑性推覆分析73．使用建模助手建立模型主菜单选择 结构>建模助手>基本结构>框架：输入：添加X 坐标，距离6，重复5；添加Z 坐标，距离6，重复3；编辑： Beta 角，90度；生成框架 材料：C30； 截面：250*600插入：插入点，0，0，0；Alpha ，-90。