最新第二章6知能优化训练

专题六标点符号的使用知能优化训练中考回顾1.(2022天津)依次填入下面一段文字方框内的标点符号,最恰当的一项是()5月18日是国际博物馆日,今年的主题是“博物馆的力量□博物馆的力量来自哪里呢□主要是来自博物馆丰富多彩的藏品□自然标本、考古遗物、艺术珍品、革命文物……不同类型的藏品记录着自然和人类文明的多元信息,蕴含着提升审美水平、厚植家国情怀、促进文明交流等多种力量。

A.”。

?:B.。

”。

:C.”。

、D.。

”?、2.(2022湖南怀化)下列句子中标点符号使用不规范的一项是()A.白杨树尤其象征了今天我们民族解放斗争中所不可缺的朴质、坚强、力求上进的精神!B.低碳生活要从身边的点滴小事做起,如随手关灯,出门选乘公交车等等……C.《沁园春·雪》开头几句“北国风光,千里冰封,万里雪飘”,充分体现了诗人崇高的思想境界。

D.“你看这段布美不美?”两个骗子问。

他们指着、描述着一些美丽的花纹——事实上它们并不存在。

3.(2022甘肃武威)阅读下面的文字,给画线句加上标点符号,最恰当的一项是()“雪如意”“雪游龙”“雪长城”,见证运动员汗水与激情的比赛场馆,则是将科技、运动与中华优秀传统文化融合的具象载体。

火种灯会徽体育图标颁奖礼服北京冬奥会视觉呈现的中国风几乎无处不在。

A.火种灯,会徽,体育图标,颁奖礼服——北京冬奥会视觉呈现的“中国风”几乎无处不在。

B.火种灯、会徽、体育图标、颁奖礼服——北京冬奥会视觉呈现的《中国风》几乎无处不在。

C.火种灯、会徽、体育图标、颁奖礼服……北京冬奥会视觉呈现的“中国风”几乎无处不在。

D.火种灯,会徽,体育图标,颁奖礼服……北京冬奥会视觉呈现的《中国风》几乎无处不在。

4.(2021天津)依次填入下面一段文字方框内的标点符号,最恰当的一项是()嫦娥五号成功返回,意味着我国已经掌握了无人月球探测技术;“天问一号”探测器着陆火星,标志着我国迈出了星际探测征程的重要一步;北斗导航星座正向地球每一个角落源源不断地送去服务信号□为什么中国航天事业既能稳步前行又能跨越发展□毫无疑问,是因为党的正确领导和国家的大力支持,是因为科技的自主创新,是因为航天人永不言败□追求卓越的精神。

人教A版高中数学选修2-3全册知能训练目录第1章1.1知能优化训练第1章1.2.1第一课时知能优化训练第1章1.2.1第二课时知能优化训练第1章1.2.2第一课时知能优化训练第1章1.2.2第二课时知能优化训练第1章1.3.1知能优化训练第1章1.3.2知能优化训练第2章2.1.1知能优化训练第2章2.1.2知能优化训练第2章2.2.1知能优化训练第2章2.2.2知能优化训练第2章2.2.3知能优化训练第2章2.3.1知能优化训练第2章2.3.2知能优化训练第2章2.4知能优化训练第3章3.1知能优化训练第3章3.2知能优化训练1．从A 地到B 地要经过C 地和D 地，从A 地到C 地有3条路，从C 地到D 地有2条路，从D 地到B 地有4条路，则从A 地到B 地不同走法的种数是( )A ．3＋2＋4＝9B ．1C ．3×2×4＝24D ．1＋1＋1＝3解析：选C.由题意从A 地到B 地需过C 、D 两地，实际就是分三步完成任务，用乘法原理．2．某学生去书店，发现3本好书，决定至少买其中一本，则购买方式共有( )A ．3种B ．6种C ．7种D ．9种解析：选C.分3类：买1本书，买2本书和买3本书，各类的购买方式依次有3种、3种和1种，故购买方式共有3＋3＋1＝7(种)．3．(2011年高考课标全国卷)有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为( )A.13B.12C.23D.34解析：选A.甲、乙两位同学参加3个小组的所有可能性有3×3＝9(种)，其中甲、乙两人参加同一个小组的情况有3(种)．故甲、乙两位同学参加同一个兴趣小组的概率P ＝39＝13. 4．将3封信投入6个信箱内，不同的投法有________种．解析：第1封信有6种投法，第2、第3封信也分别有6种投法，因此共有6×6×6＝216种投法．答案：216一、选择题1．现有4件不同款式的上衣和3条不同颜色的长裤，如果一条长裤与一件上衣配成一套，则不同的配法种数为( )A ．7B ．12C ．64D ．81解析：选B.要完成配套，分两步：第1步，选上衣，从4件上衣中任选一件，有4种不同选法；第2步，选长裤，从3条长裤中任选一条，有3种不同选法．故共有4×3＝12种不同的配法．2．从A 地到B 地，可乘汽车、火车、轮船三种交通工具，如果一天内汽车发3次，火车发4次，轮船发2次，那么一天内乘坐这三种交通工具的不同走法为( )A ．1＋1＋1＝3B ．3＋4＋2＝9C ．3×4×2＝24D ．以上都不对答案：B3．十字路口来往的车辆，如果不允许回头，共有不同的行车路线( )A ．24种B ．16种C ．12种D ．10种解析：选C.完成该任务可分为四类，从每一个方向入口都可作为一类，如图：从第1个入口进入时，有3种行车路线；同理，从第2个，第3个，第4个入口进入时，都分别有3种行车路线，由分类加法计数原理可得共有3＋3＋3＋3＝12种不同的行车路线，故选C.4．从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a，b组成复数a＋b i，其中虚数有() A．30个B．42个C．36个D．35个解析：选C.第一步取b的数，有6种方法，第二步取a的数，也有6种方法，根据乘法计数原理，共有6×6＝36种方法．5．从集合{1,2,3,4,5}中任取2个不同的数，作为直线Ax＋By＝0的系数，则形成不同的直线最多有()A．18条B．20条C．25条D．10条解析：选A.第一步取A的值，有5种取法，第二步取B的值有4种取法，其中当A＝1，B＝2时，与A＝2，B＝4时是相同的；当A＝2，B＝1时，与A＝4，B＝2时是相同的，故共有5×4－2＝18(条)．6．用1,2,3三个数字组成一个四位数，规定这三个数必须全部使用，且同一数字不能相邻出现，这样的四位数有()A．36个B．18个C．9个D．6个解析：选B.分3步完成，1,2,3这三个数中必有某一个数字被使用2次．第1步，确定哪一个数字被使用2次，有3种方法；第2步，把这2个相同的数字排在四位数不相邻的两个位置上有3种方法；第3步，将余下的2个数字排在四位数余下的两个位置上，有2种方法．故有3×3×2＝18个不同的四位数．二、填空题7．加工某个零件分三道工序，第一道工序有5人，第二道工序有6人，第三道工序有4人，从中选3人每人做一道工序，则选法有________种．解析：选第一、第二、第三道工序各一人的方法数依次为5、6、4，由分步乘法计数原理知，选法总数为N＝5×6×4＝120.答案：1208．如图是某校的校园设施平面图，现用不同的颜色作为各区域的底色，为了便于区分，要求相邻区域不能使用同一种颜色．若有6种不同的颜色可选，则有________种不同的着色方案．解析：操场可从6种颜色中任选1种着色；餐厅可从剩下的5种颜色中任选1种着色；宿舍区和操场、餐厅颜色都不能相同，故可从其余的4种颜色中任选1种着色；教学区和宿舍区、餐厅的颜色都不能相同，故可从其余的4种颜色中任选1种着色．根据分步乘法计数原理，共有6×5×4×4＝480种着色方案．答案：4809．从1,2,3,4,7,9六个数中，任取两个数作对数的底数和真数，则所有不同的对数的值的个数为________．解析：(1)当取1时，1只能为真数，此时对数的值为0.(2)不取1时，分两步：①取底数，5种；②取真数，4种．其中log23＝log49，log32＝log94，log24＝log39，log42＝log93，∴N＝1＋5×4－4＝17.答案：17三、解答题10．8张卡片上写着0,1,2，…，7共8个数字，取其中的三张卡片排放在一起，可组成多少个不同的三位数？解：先排放百位，从1,2，…，7共7个数中选一个有7种选法；再排十位，从除去百位的数外，剩余的7个数(包括0)中选一个，有7种选法；最后排个位，从除前两步选出的数外，剩余的6个数中选一个，有6种选法．由分步乘法计数原理，共可以组成7×7×6＝294个不同的三位数．11．从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种，分别种在不同土质的三块土地上，其中黄瓜必须种植，求有多少种不同的种植方法？解：若黄瓜种在第一块土地上，则有3×2×1＝6种不同种植方法．同理，黄瓜种在第二块、第三块土地上，均有3×2×1＝6(种)．故不同的种植方法共有6×3＝18(种)．12．某校学生会由高一年级5人，高二年级6人，高三年级4人组成．(1)选其中一人为学生会主席，有多少种不同的选法？(2)若每年级选1人为校学生会常委成员，有多少种不同的选法？(3)若要选出不同年级的两人分别参加市里组织的两项活动，有多少种不同的选法？解：(1)分三类：第一类，从高一年级选一人，有5种选择；第二类，从高二年级选一人，有6种选择；第三类，从高三年级选一人，有4种选择．由分类加法计数原理，共有5＋6＋4＝15种选法．(2)分三步完成：第一步，从高一年级选一人，有5种选择；第二步，从高二年级选一人，有6种选择；第三步，从高三年级选一人，有4种选择．由分步乘法计数原理，共有5×6×4＝120种选法．(3)分三类：高一、高二各一人，共有5×6＝30种选法；高一、高三各一人，共有5×4＝20种选法；高二、高三各一人，共有6×4＝24种选法；由分类加法计数原理，共有30＋20＋24＝74种选法．1．用1,2,3,4,5这5个数字，组成无重复数字的三位数，其中奇数共有()A．30个B．36个C．40个D．60个解析：选B.分2步完成：个位必为奇数，有A13种选法；从余下的4个数中任选2个排在三位数的百位、十位上，有A24种选法．由分步乘法计数原理，共有A13×A24＝36个无重复数字的三位奇数．2．6人站成一排，甲、乙、丙3个人不能都站在一起的排法种数为()A．720 B．144C．576 D．684解析：选C.(间接法)甲、乙、丙三人在一起的排法种数为A44×A33；不考虑任何限制，6人的全排列有A66.∴符合题意的排法种数为：A66－A44×A33＝576.3．某班新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目，如果将这两个节目插入原节目单中，那么不同插法种数为()A．42 B．30C．20 D．12解析：选A.分两类：①两个新节目相邻的插法有6A22种；②两个新节目不相邻的插法有A26种．故N＝6×2＋6×5＝42.4．将红、黄、蓝、白、黑5种颜色的小球，分别放入红、黄、蓝、白、黑5种颜色的小口袋中，若不允有空袋，且红口袋中不能装入红球，则有______种不同的放法．解析：先装红球，且每袋一球，所以有A14×A44＝96(种)．答案：96一、选择题1．高三(1)班需要安排毕业晚会的4个音乐节目，2个舞蹈节目和1个曲艺节目的演出顺序，要求两个舞蹈节目不连排，则不同排法的种数是()A．1800 B．3600C．4320 D．5040解析：选B.利用插空法，先将4个音乐节目和1个曲艺节目全排列有A55种，然后从6个空中选出2个空将舞蹈节目全排列有A26种，所以共有A55A26＝3600(种)．故选B.2．某省有关部门从6人中选4人分别到A、B、C、D四个地区调研十二五规划的开局形势，要求每个地区只有一人，每人只去一个地区，且这6人中甲、乙两人不去A地区，则不同的安排方案有()A．300种B．240种C．144种D．96种解析：选B.A地区有A14种方法，其余地区有A35种方法，共有A14A35＝240(种)．3．用数字1,2,3,4,5可以组成没有重复数字，并且比20000大的五位偶数共有() A．48个B．36个C．24个D．18个解析：选B.个位数字是2的有3A33＝18(个)，个位数字是4的有3A33＝18(个)，所以共有36个．4．8名学生和2位老师站成一排合影，2位老师不相邻的排法种数为()A．A88A29B．A88A210C．A88A27D．A88A26解析：选A.运用插空法，8名学生间共有9个空隙(加上边上空隙)，先把老师排在9个空隙中，有A29种排法，再把8名学生排列，有A88种排法，共有A88×A29种排法．5．五名男生与两名女生排成一排照相，如果男生甲必须站在中间，两名女生必须相邻，符合条件的排法共有()A．48种B．192种C．240种D．288种解析：选B.(用排除法)将两名女生看作1人，与四名男生一起排队，有A55种排法，而女生可互换位置，所以共有A55×A22种排法，男生甲插入中间位置，只有一种插法；而4男2女排列中2名女生恰在中间的排法共有A22×A44(种)，这时男生甲若插入中间位置不符合题意，故符合题意的排列总数为A55×A22－A44×A22＝192.6．由1、2、3、4、5组成没有重复数字且1、2都不与5相邻的五位数的个数是() A．36 B．32C．28 D．24解析：选A.分类：①若5在首位或末位，共有2A12×A33＝24(个)；②若5在中间三位，共有A13×A22×A22＝12(个)．故共有24＋12＝36(个)．二、填空题7．5人站成一排，甲必须站在排头或排尾的不同站法有________种．解析：2A44＝48.答案：488．3个人坐8个位置，要求每人的左右都有空位，则有________种坐法．解析：第一步：摆5个空位置，○○○○○；第二步：3个人带上凳子插入5个位置之间的四个空，有A34＝24(种)，故有24种不同坐法．答案：249．5名大人要带两个小孩排队上山，小孩不排在一起也不排在头、尾，则共有________种排法(用数字作答)．解析：先让5名大人全排列有A55种排法，两个小孩再依条件插空有A24种方法，故共有A55A24＝1440种排法．答案：1440三、解答题10．7名班委中有A、B、C三人，有7种不同的职务，现对7名班委进行职务具体分工．(1)若正、副班长两职只能从A、B、C三人中选两人担任，有多少种分工方案？(2)若正、副班长两职至少要选A、B、C三人中的一人担任，有多少种分工方案？解：(1)先排正、副班长有A23种方法，再安排其余职务有A55种方法，依分步计数原理，共有A23A55＝720种分工方案．(2)7人中任意分工方案有A77种，A、B、C三人中无一人任正、副班长的分工方案有A24 A55种，因此A、B、C三人中至少有一人任正、副班长的方案有A77－A24A55＝3600(种)．11．用0,1,2,3,4,5这六个数字：(1)能组成多少个无重复数字的四位偶数？(2)能组成多少个无重复数字且为5的倍数的五位数？(3)能组成多少个无重复数字的比1325大的四位数？解：(1)符合要求的四位偶数可分为三类：第一类：0在个位时，有A 35个；第二类：2在个位时，首位从1,3,4,5中选定1个有A 14种，十位和百位从余下的数字中选，有A 24种，于是有A 14×A 24(个)；第三类：4在个位时，与第二类同理，也有A 14×A 24(个)．由分类加法计数原理得：共有A 35＋2A 14×A 24＝156(个)．(2)为5的倍数的五位数可分为两类：第一类：个位上为0的五位数有A 45个；第二类：个位上为5的五位数有A 14×A 34(个)，故满足条件的五位数共有A 45＋A 14×A 34＝216(个)．(3)比1325大的四位数可分为三类：第一类：形如2，3 ，4 ，5 ，共有A 14×A 35(个)；第二类：形如14 ，15 ，共有A 12×A 24(个)； 第三类：形如134 ，135 ，共有A 12×A 13(个)．由分类加法计数原理可得，比1325大的四位数共有：A 14×A 35＋A 12×A 24＋A 12×A 13＝270(个)．12．7名师生站成一排照相留念，其中老师1人，男学生4人，女学生2人，在下列情况下，各有多少种不同站法？(1)两名女生必须相邻而站；(2)4名男生互不相邻；(3)若4名男生身高都不等，按从高到低的顺序站；(4)老师不站中间，女生不站两端．解：(1)2名女生站在一起有站法A 22种，视为一种元素与其余5人全排，有A 66种排法，所以有不同站法A 22×A 66＝1440(种)．(2)先站老师和女生，有站法A 33种，再在老师和女生站位的间隔(含两端)处插入男生，每空一人，则插入方法A 44种，所以共有不同站法A 33×A 44＝144(种)．(3)7人全排列中，4名男生不考虑身高顺序的站法有A 44种，而由高到低有从左到右和从右到左的不同，所以共有不同站法2×A 77A 44＝420(种)． (4)中间和两侧是特殊位置，可分类求解如下：①老师站在两侧之一，另一侧由男生站，有A 12×A 14×A 55种站法；②两侧全由男生站，老师站除两侧和正中的另外4个位置之一，有A 14×A 24×A 44种站法，所以共有不同站法A 12×A 14×A 55＋A 14×A 24×A 44＝960＋1152＝2112(种)．1．5A35＋4A24＝()A．107B．323C．320 D．348解析：选D.原式＝5×5×4×3＋4×4×3＝348.2．4×5×6×…·(n－1)·n等于()A．A4n B．A n－4nC．n！－4! D．A n－3n解析：选D.原式可写成n·(n－1)·…×6×5×4，故选D.3．6名学生排成两排，每排3人，则不同的排法种数为()A．36 B．120C．720 D．240解析：选C.排法种数为A66＝720.4．下列问题属于排列问题的是________．①从10个人中选2人分别去种树和扫地；②从10个人中选2人去扫地；③从班上30名男生中选出5人组成一个篮球队；④从数字5,6,7,8中任取两个不同的数作幂运算．解析：①选出的2人有不同的劳动内容，相当于有顺序．②选出的2人劳动内容相同，无顺序．③5人一组无顺序．④选出的两个数作为底数或指数其结果不同，有顺序．答案：①④一、选择题1．甲、乙、丙三地客运站，需要准备在甲、乙、丙三地之间运行的车票种数是() A．1 B．2C．3 D．6解析：选D.A23＝6.2．已知A2n＋1－A2n＝10，则n的值为()A．4 B．5C．6 D．7解析：选B.由A2n＋1－A2n＝10，得(n＋1)n－n(n－1)＝10，解得n＝5.3．从5本不同的书中选两本送给2名同学，每人一本，则不同的送法种数是() A．5 B．10C．20 D．60解析：选C.A25＝20.4．将3张不同的电影票分给10人中的3人，每人一张，则不同的分法种数是() A．2160 B．720C．240 D．120解析：选B.A310＝10×9×8＝720.5．某段铁路所有车站共发行132种普通车票，那么这段铁路共有车站数是()A．8 B．12C．16 D．24解析：选B.设车站数为n，则A2n＝132，n(n－1)＝132，∴n ＝12.6．S ＝1！＋2！＋3！＋…＋99！，则S 的个位数字为( )A ．0B ．3C ．5D ．7解析：选B.∵1！＝1,2！＝2,3！＝6,4！＝24,5！＝120,6！＝720，…∴S ＝1！＋2！＋3！＋…＋99！的个位数字是3.二、填空题7．若A m 10＝10×9×…×5，则m ＝________.解析：10－m ＋1＝5，得m ＝6.答案：68．A n ＋32n ＋A n ＋14＝________.解析：由⎩⎪⎨⎪⎧ n ＋3≤2n ，n ＋1≤4，n ∈N *，得n ＝3， ∴A n ＋32n ＋A n ＋14＝6！＋4！＝744. 答案：7449．甲、乙、丙、丁四人轮读同一本书，则甲首先读的安排方法有________种． 解析：甲在首位，相当于乙、丙、丁全排，即3！＝3×2×1＝6.答案：6三、解答题10．解不等式：A x 9>6A x －29.解：原不等式可化为9！(9－x )！>6·9！(9－x ＋2)！， 其中2≤x ≤9，x ∈N *，∴(11－x )(10－x )>6，即x 2－21x ＋104>0，∴(x －8)(x －13)>0，∴x <8或x >13.又∵2≤x ≤9，x ∈N *，∴2≤x <8，x ∈N *.故x ＝2,3,4,5,6,7.11．解方程3A x 8＝4A x －19.解：由3A x 8＝4A x －19得3×8！(8－x )！＝4×9！(10－x )！. ∴3×8！(8－x )！＝4×9×8！(10－x )(9－x )(8－x )！. 化简得：x 2－19x ＋78＝0，解得x 1＝6，x 2＝13.∵x ≤8，且x －1≤9，∴原方程的解是x ＝6.12．判断下列问题是否为排列问题．(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同)；(2)选2个小组分别去植树和种菜；(3)选2个小组去种菜；(4)选10人组成一个学习小组；(5)选3个人分别担任班长、学习委员、生活委员；(6)某班40名学生在假期相互通信．解：(1)中票价只有三种，虽然机票是不同的，但票价是一样的，不存在顺序问题，所以不是排列问题；(2)植树和种菜是不同的，存在顺序问题，属于排列问题；(3)、(4)不存在顺序问题，不属于排列问题；(5)中每个人的职务不同，例如甲当班长或当学习委员是不同的，存在顺序问题，属于排列问题；(6)A给B写信与B给A写信是不同的，所以存在着顺序问题，属于排列问题．所以在上述各题中(2)、(5)、(6)属于排列问题．1．编号为1、2、3、4、5、6、7的七盏路灯，晚上用时只亮三盏灯，且任意两盏亮灯不相邻，则不同的开灯方案有( )A ．60种B ．20种C ．10种D ．8种解析：选C.四盏熄灭的灯产生的5个空档中放入3盏亮灯，即C 35＝10.2．某中学要从4名男生和3名女生中选4人参加公益劳动，若男生甲和女生乙不能同时参加，则不同的选派方案共有( )A ．25种B ．35种C ．820种D ．840种解析：选A.分3类完成：男生甲参加，女生乙不参加，有C 35种选法；男生甲不参加，女生乙参加，有C 35种选法；两人都不参加，有C 45种选法．所以共有2C 35＋C 45＝25(种)不同的选派方案．3．(2010年高考大纲全国卷Ⅰ)某校开设A 类选修课3门，B 类选修课4门，一位同学从中共选3门．若要求两类课程中各至少选一门，则不同的选法共有( )A ．30种B ．35种C ．42种D ．48种解析：选A.法一：可分两种互斥情况：A 类选1门，B 类选2门或A 类选2门，B 类选1门，共有C 13C 24＋C 23C 14＝18＋12＝30种选法．法二：总共有C 37＝35种选法，减去只选A 类的C 33＝1(种)，再减去只选B 类的C 34＝4(种)，故有30种选法．4．(2011年高考江苏卷)从1,2,3,4这四个数中一次随机地取两个数，则其中一个数是另一个数的两倍的概率是________．解析：从1,2,3,4中任取两个数的组合个数为C 24＝6，满足一个数是另一个数两倍的组合为{1,2}，{2,4}，故P ＝26＝13.答案：13一、选择题1．9名会员分成三组讨论问题，每组3人，共有不同的分组方法种数为( )A ．C 39C 36B ．A 39A 36C.C 39C 36A 33 D ．A 39A 36A 33 解析：选C.此为平均分组问题，要在分组后除以三组的排列数A 33.2．5本不同的书全部分给4个学生，每个学生至少1本，不同的分法种数有( ) A ．480 B ．240 C ．120 D ．96 解析：选B.先把5本书中两本捆起来，再分成4份即可，∴分法数为C 25A 44＝240.3．某班级要从4名男生、2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案种数为( )A ．14B ．24C ．28D ．48解析：选A.6人中选4人的方案有C 46＝15(种)，没有女生的方案只有一种，所以满足要求的方案总数有14种．4．已知圆上9个点，每两点连一线段，所有线段在圆内的交点有( ) A ．36个 B ．72个 C ．63个 D ．126个解析：选D.此题可化归为：圆上9个点可组成多少个四边形，每个四边形的对角线的交点即为所求，所以，交点有C 49＝126(个)．5．(2010年高考大纲全国卷Ⅱ)将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中，若每个信封放2张，其中标号为1,2的卡片放入同一信封，则不同的放法共有( )A ．12种B ．18种C ．36种D ．54种解析：选B.先将1,2捆绑后放入信封中，有C 13种方法，再将剩余的4张卡片放入另外两个信封中，有C 24C 22种方法，所以共有C 13C 24C 22＝18种方法．6．如图所示的四棱锥中，顶点为P ，从其他的顶点和各棱中点中取3个，使它们和点P 在同一平面内，不同的取法种数为( )A ．40B ．48C ．56D ．62解析：选C.满足要求的点的取法可分为3类：第1类，在四棱锥的每个侧面上除点P 外任取3点，有4C 35种取法； 第2类，在两个对角面上除点P 外任取3点，有2C 34种取法；第3类，过点P 的四条棱中，每一条棱上的两点和与这条棱异面的两条棱的中点也共面，有4C 12种取法．所以，满足题意的不同取法共有4C 35＋2C 34＋4C 12＝56(种)． 二、填空题7．在50件产品中有4件是次品，从中任意抽出5件，至少有三件是次品的抽法共有________种．解析：分两类，有4件次品的抽法为C 44C 146(种)；有三件次品的抽法有C 34C 246(种)，所以共有C 44C 146＋C 34C 246＝4186种不同的抽法．答案：41868．某运动队有5对老搭档运动员，现抽派4个运动员参加比赛，则这4人都不是老搭档的抽派方法数为________．解析：先抽取4对老搭档运动员，再从每对老搭档运动员中各抽1人，故有C 45C 12C 12C 12C 12＝80(种)． 答案：809．2011年3月10日是第六届世界肾脏日，某社区服务站将5位志愿者分成3组，其中两组各2人，另一组1人，分别去三个不同的社区宣传这届肾脏日的主题：“保护肾脏，拯救心脏”，不同的分配方案有________种．(用数字作答)解析：分配方案有C 25C 23C 11A 22×A 33＝10×3×62＝90(种)． 答案：90三、解答题 10．四个不同的小球放入编号为1,2,3,4的四个盒子中，恰有一个空盒的放法有多少种？ 解：恰有一个空盒，则另外三个盒子中小球数分别为1,1,2，实际上可转化为先将四个不同的小球分为三组，两组各1个，另一组2个，分组方法有C 14C 13C 22A 22(种)，然后将这三组再加上一个空盒进行全排列，即共有C 14C 13C 22A 22·A 44＝144(种)． 11．要从7个班中选10人参加数学竞赛，每班至少1人，共有多少种不同的选法？解：法一：共分三类：第一类：一个班出4人，其余6个班各出1人，有C 17种；第二类：有2个班分别出2人，3人，其余5个班各出1人，有A 27种；第三类：有3个班各出2人，其余4个班各出1人，有C 37种，故共有C 17＋A 27＋C 37＝84(种)．法二：将10人看成10个元素，这样元素之间共有9个空(两端不计)，从这9个空中任选6个(即这6个位置放入隔板，将其分为七部分)，有C 69＝84种放法．故共有84种不同的选法．12．如图，在以AB 为直径的半圆周上，有异于A 、B 的六个点C 1、C 2、C 3、C 4、C 5、C 6，直径AB 上有异于A 、B 的四个点D 1、D 2、D 3、D 4.(1)以这10个点中的3个点为顶点作三角形可作出多少个？其中含C 1点的有多少个？ (2)以图中的12个点(包括A 、B )中的4个点为顶点，可作出多少个四边形？解：(1)可分三种情况处理：①C 1、C 2、…、C 6这六个点任取三点可构成一个三角形；②C 1、C 2、…、C 6中任取一点，D 1、D 2、D 3、D 4中任取两点可构成一个三角形； ③C 1、C 2、…、C 6中任取两点，D 1、D 2、D 3、D 4中任取一点可构成一个三角形．∴C 36＋C 16C 24＋C 26C 14＝116(个)．其中含C 1点的三角形有C 25＋C 15·C 14＋C 24＝36(个)． (2)构成一个四边形，需要四个点，且无三点共线，∴共有C 46＋C 36C 16＋C 26C 26＝360(个)．1．计算C 28＋C 38＋C 29等于() A ．120 B ．240C ．60D ．480解析：选A.原式＝C 39＋C 29＝C 310＝120.2．若C 7n ＋1－C 7n ＝C 8n ，则n 等于( ) A ．12 B ．13 C ．14 D ．15解析：选C.C 7n ＋1－C 7n ＝C 8n ，即C 7n ＋1＝C 8n ＋C 7n ＝C 8n ＋1，所以n ＋1＝7＋8，即n ＝14. 3．某校一年级有5个班，二年级有8个班，三年级有3个班，分年级举行班与班之间的篮球单循环赛，总共需进行比赛的场数是( )A ．C 25＋C 28＋C 23B ．C 25C 28C 23C ．A 25＋A 28＋A 23 D ．C 216解析：选A.分三类：一年级比赛的场数是C 25，二年级比赛的场数是C 28，三年级比赛的场数是C 23，再由分类加法计数原理可求．4．把8名同学分成两组，一组5人学习电脑，一组3人做生物实验，则不同的安排方法有________种．解析：C 38＝56. 答案：56一、选择题1．下面几个问题中属于组合问题的是( )①由1,2,3,4构成的双元素集合；②5个队进行单循环足球比赛的分组情况；③由1,2,3构成两位数的方法；④由1,2,3组成无重复数字的两位数的方法．A ．①③B ．②④C ．①②D ．①②④ 答案：C2．已知平面内A 、B 、C 、D 这4个点中任何3点均不共线，则由其中任意3个点为顶点的所有三角形的个数为( )A ．3B ．4C ．12D ．24解析：选B.C 34＝4.3．C 03＋C 14＋C 25＋C 36＋…＋C 1720的值为( ) A ．C 321 B ．C 320C ．C 420 D ．C 421 解析：选D.原式＝()C 04＋C 14＋C 25＋C 36＋…＋C 1720 ＝()C 15＋C 25＋C 36＋…＋C 1720＝(C 26＋C 36)＋…＋C 1720＝C 1721＝C 21－1721＝C 421. 4．若A 3n ＝12C 2n ，则n 等于( ) A ．8 B ．5或6 C ．3或4 D ．4解析：选A.A 3n ＝n (n －1)(n －2)，C 2n ＝12n (n －1)，∴n (n －1)(n －2)＝6n (n －1)，又n ∈N *，且n ≥3.解得n ＝8.5．从6位同学中选出4位参加一个座谈会，要求张、王两人中至多有一个人参加，则不同选法的种数为( )A ．9B ．14C ．12D ．15解析：选A.法一：直接法：分两类，第一类张、王两人都不参加，有C 44＝1种选法；第二类张、王两人只有1人参加，有C 12C 34＝8种选法．故共有C 44＋C 12×C 34＝9种选法．法二：间接法：C 46－C 24＝9(种)．6．把三张游园票分给10个人中的3人，分法有( ) A ．A 310种 B ．C 310种C ．C 310A 310种D ．30种 解析：选B.三张票没区别，从10人中选3人即可，即C 310. 二、填空题7．若C 13n ＝C 7n ，则C 18n ＝________.解析：∵C 13n ＝C 7n ，∴13＝n －7，∴n ＝20， ∴C 1820＝C 220＝190. 答案：1908．C 22＋C 23＋C 24＋…＋C 210＝________. 解析：原式＝C 33＋C 23＋C 24＋…＋C 210＝C 34＋C 24＋…＋C 210＝C 35＋C 25＋…＋C 210＝C 311＝165. 答案：1659．从4名男生和3名女生中选出4人担任奥运志愿者，若选出的4人中既有男生又有女生，则不同的选法共有________________________________________________________________________种．解析：(间接法)共有C 47－C 44＝34种不同的选法． 答案：34 三、解答题10．若C 4n >C 6n ，求n 的取值集合． 解：∵C 4n >C 6n ，∴⎩⎪⎨⎪⎧C 4n >C 6n n ≥6⇒⎩⎨⎧n ！4！(n －4)！>n ！6！(n －6)！n ≥6⇒⎩⎨⎧ n 2－9n －10<0n ≥6⇒⎩⎨⎧－1<n <10，n ≥6.∵n ∈N *，∴n ＝6、7、8、9，∴n 的集合为{6,7,8,9}．11．要从6男4女中选出5人参加一项活动，按下列要求，各有多少种不同的选法？ (1)甲当选且乙不当选；(2)至少有1女且至多有3男当选．解：(1)甲当选且乙不当选，∴只需从余下的8人中任选4人，有C 48＝70种选法．(2)至少有1女且至多有3男时，应分三类：第一类是3男2女，有C 36C 24种选法； 第二类是2男3女，有C 26C 34种选法； 第三类是1男4女，有C 16C 44种选法．由分类计数原理知，共有C 36C 24＋C 26C 34＋C 16C 44＝186种选法． 12．现有10件产品，其中有2件次品，任意抽出3件检查． (1)正品A 被抽到有多少种不同的抽法？ (2)恰有一件是次品的抽法有多少种？ (3)至少一件是次品的抽法有多少种？解：(1)C 29＝9×82＝36(种)．(2)从2件次品中任取1件有C 12种方法，从8件正品中取2件有C 28种方法，由分步乘法计数原理，不同的抽法共有C 12×C 28＝2×8×72＝56(种)． (3)法一：含1件次品的抽法有C 12C 28种，含2件次品的抽法有C 22×C 18种，由分类加法计数原理，不同的抽法共有C 12×C 28＋C 22×C 18＝56＋8＝64(种)．法二：从10件产品中任取3件的抽法为C 310种，不含次品的抽法有C 38种，所以至少1件次品的抽法为C 310－C 38＝64(种)．1．(x ＋2)6的展开式中x 3的系数是( ) A ．20 B ．40 C ．80 D ．160解析：选D.法一：设含x 3的为第r ＋1项，则T r ＋1＝C r n x6－r ·2r，令6－r ＝3，得r ＝3，故展开式中x 3的系数为C 36×23＝160.法二：根据二项展开式的通项公式的特点：二项展开式每一项中所含的x 与2分得的次数和为6，则根据条件满足条件x 3的项按3与3分配即可，则展开式中x 3的系数为C 36×23＝160.2．(2x －12x)6的展开式的常数项是( )A ．20B ．－20C ．40D ．－40解析：选B.由题知(2x －12x )6的通项为T r ＋1＝(－1)r C r 626－2r x 6－2r，令6－2r ＝0得r ＝3，故常数项为(－1)3C 36＝－20.3．1.056的计算结果精确到0.01的近似值是( ) A ．1.23 B ．1.24 C ．1.33 D ．1.34解析：选 D.1.056＝(1＋0.05)6＝C 06＋C 16×0.05＋C 26×0.052＋C 36×0.053＋…＝1＋0.3＋0.0375＋0.0025＋…≈1.34.4．(2011年高考浙江卷)设二项式⎝⎛⎭⎫x －a x 6(a >0)的展开式中x 3的系数是A ，常数项为B ，若B ＝4A ，则a 的值是________．解析：A ＝C 26(－a )2，B ＝C 46(－a )4， 由B ＝4A 知，4C 26(－a )2＝C 46(－a )4，解得a ＝±2. 又∵a >0，∴a ＝2. 答案：2一、选择题1．在(1－x )5－(1－x )6的展开式中，含x 3的项的系数是( ) A ．－5 B ．5 C ．－10 D ．10解析：选D.(1－x )5中x 3的系数－C 35＝－10，－(1－x )6中x 3的系数为－C 36·(－1)3＝20，故(1－x )5－(1－x )6的展开式中x 3的系数为10.2．(x －2y )10的展开式中x 6y 4项的系数是( ) A ．840 B ．－840 C ．210 D ．－210解析：选A.在通项公式T r ＋1＝C r 10(－2y )r x10－r 中，令r ＝4，即得(x －2y )10的展开式中x 6y 4项的系数为C 410·(－2)4＝840.3．(2010年高考陕西卷)⎝⎛⎭⎫x ＋ax 5(x ∈R )展开式中x 3的系数为10，则实数a 等于( ) A ．－1 B.12 C ．1D ．2解析：选D.由二项式定理，得T r ＋1＝C r 5x 5－r ·⎝⎛⎭⎫a x r ＝C r 5·x 5－2r ·a r ，∴5－2r ＝3，∴r ＝1，∴C 15·a ＝10，∴a ＝2.4．若C 1n x ＋C 2n x 2＋…＋C n n x n能被7整除，则x ，n 的值可能为( ) A ．x ＝4，n ＝3 B ．x ＝4，n ＝4 C ．x ＝5，n ＝4 D ．x ＝6，n ＝5解析：选C.由C 1n x ＋C 2n x 2＋…＋C n n x n ＝(1＋x )n－1，分别将选项A 、B 、C 、D 代入检验知，仅有C 适合．5.⎝⎛⎭⎫x －13x 10的展开式中含x 的正整数指数幂的项数是( ) A ．0 B ．2 C ．4 D ．6解析：选B.T r ＋1＝C r 10x 10－r 2·⎝⎛⎭⎫－13r ·x －r ＝C r 10⎝⎛⎭⎫－13r ·x 10－3r2.若是正整数指数幂，则有10－3r2为正整数，∴r 可以取0,2，∴项数为2.6．(1＋2x )3(1－3x )5的展开式中x 的系数是( ) A ．－4 B ．－2 C ．2 D ．4解析：选C.(1＋2x )3(1－3x )5＝(1＋6x 12＋12x ＋8x 32)·(1－5x 13＋10x 23－10x ＋5x 43－x 53)，x的系数是－10＋12＝2.二、填空题 7.⎝⎛⎭⎪⎫2－13x 6的展开式中的第四项是________．解析：T 4＝C 3623⎝⎛⎭⎪⎫－13x 3＝－160x .答案：－160x8．若(x ＋a )5的展开式中的第四项是10a 2(a 为大于0的常数)，则x ＝________.解析：∵T 4＝C 35(x )2·a 3＝10x ·a 3. ∴10xa 3＝10a 2(a >0)，∴x ＝1a.答案：1a9．(2010年高考辽宁卷)(1＋x ＋x 2)⎝⎛⎭⎫x －1x 6的展开式中的常数项为__________． 解析：(1＋x ＋x 2)⎝⎛⎭⎫x －1x 6＝(1＋x ＋x 2)[ C 06x 6⎝⎛⎭⎫－1x 0＋C 16x 5⎝⎛⎭⎫－1x 1＋C 26x 4⎝⎛⎭⎫－1x 2＋C 36x 3⎝⎛⎭⎫－1x 3。

一、基础运用1．下列各组词语中书写有误的一项是()A．筹措藐视篑乏目光炯炯B．会晤摒弃追溯扣人心弦C．桎梏颓废遵循陈腐不堪D．歪曲嫌恶妨碍毫无例外解析：选A。

A项“篑乏”的“篑”应为“匮”。

2．下列各组句子中加点的词语使用正确的一项是()A．在这里，马克思用整周整周的时间阅读各种经济和政治文献，作了摘录，并充分熟悉英国工人运动的思想财富或．实际经验。

B．所以人类始终只提出自己能够解决的任务，因为只要仔细考查．．就可以发现，任务本身，只有在解决它的物质条件已经存在或者至少是在形成过程中的时候，才会发生。

C．时间一个月一个月地过去了，情况日益清楚地表明，在正义者同盟和其他工人组织中进行一次思想上的澄清工作是多么．．刻不容缓。

D．马克思力图使他理解无产阶级需要的是科学的理论，而不是单纯诉诸．．于他们的感情和朴素阶级本能的宣传。

解析：选C。

A“或”应改为“和”；B“考查”应为“考察”；D“诉诸”中的“诸”与后文“于”重复。

3．下列句子没有语病的一项是()A．人心向背，是决定一个政党、一个政权兴盛的根本因素，真正的马克思主义政党，从来都牢记这个真理。

B．中国人民自从接受了马列主义思想以后，中国的革命就在毛泽东同志领导下大大改变了样子。

C．通过一个个伟人的逝世，不时地使那些疑虑重重受怀疑论折磨的人对宗教产生动摇。

上天让人民面对崇高的奥秘并对死亡加以思考的时候，知道了死亡是伟大的自由这一事实。

D．只有当劳动与兴趣、爱好乃至理想有机地结合在一起的时候，潜藏在每个人身上的想象力和创造力，才能够最大程度地发挥出来。

解析：选D。

A项一面对两面搭配不当，政权兴盛的因素应该是人心所向而不可能是“背”。

B项句子前后主语不一致，应该将“自从”调至“中国人民”前。

C项滥用介词，淹没主语，应删去“通过”。

二、课内阅读阅读下面的文字，回答4～6题。

早在1845年春，马克思就曾把他的哲学中这种革命化的新特点用这样一句简明而又确切的话表述出来了：“哲学家只是用不同的方式解释世界，而问题在于改变世界。

§2．3.1 向量数量积的物理背景与定义2．3.2 向量数量积的运算律1．有4个式子：①0·a ＝0；②0·a ＝0；③0－AB →＝BA →；④|a ·b |＝|a ||b |，其中正确的个数为( )A ．4B ．3C ．2D ．1解析：选C.0·a ＝|0|·|a |cos θ＝0，故①正确，②错误；0－AB →＝0＋BA →＝BA →，故③正确；而|a ·b |＝||a ||b |cos θ|＝|a |·|b |·|cos θ|，故④错误，从而选C.2．已知向量a 和向量b 的夹角为30°，|a |＝2，|b |＝3，则向量a 和向量b 的数量积a ·b ＝( )A ．3B ．1C.32D ．2 解析：选A.a ·b ＝|a |·|b |·cos 〈a ，b 〉＝2×3×32＝3. 3．向量a ，b 满足a·b ＝－40，|a |＝10，|b |＝8，则向量a ，b 的夹角为( )A ．60°B ．－60°C ．120°D ．－120°解析：选C.cos 〈a ，b 〉＝a·b |a||b|＝－4010×8＝－12. ∴〈a ，b 〉＝120°.4．已知〈a ，b 〉＝120°，|a |＝2，|b |＝3，则|a ＋b |＝________.解析：|a ＋b |2＝a 2＋2a ·b ＋b 2＝4＋2×2×3×⎝⎛⎭⎫－12＋9＝7. 答案：7一、选择题1．下列命题正确的是( )①0·0＝0；②a ·b ＝b ·a ；③|a ·b |≤a ·b .A ．①②B ．②③C ．①③D ．①②③解析： 选 A.①正确；a ·b ＝|a ||b |cos θ＝|b ||a |cos θ＝b ·a ，②正确；|a ·b |＝||a ||b |·cos θ|＝|a ||b ||cos θ|≥|a |·|b |cos θ＝a ·b ，③错误，故选A.2．若|a |＝4，|b |＝6，a 与b 的夹角为135°，则a ·(－b )等于( )A ．12B ．－12C ．12 2D ．－12 2解析：选C.∵a 与－b 的夹角为45°，∴a ·(－b )＝|a |·|－b |·cos45°＝4×6×22＝12 2. 3．已知|a |＝1，|b |＝6，a ·(b －a )＝2，则向量a 与b 的夹角为( )A.π6B.π4C.π3D.π2解析：选C.∵a ·(b －a )＝a ·b －a 2＝2，又|a |＝1，∴a ·b ＝3，即|a ||b |cos 〈a ，b 〉＝3＝1×6cos 〈a ，b 〉，得cos 〈a ，b 〉＝12， ∴a 与b 的夹角为π3，故选C. 4．(2011年聊城高一检测)已知|a |＝6，|b |＝4，a 与b 的夹角为60°，则(a ＋2b )·(a －3b )等于( )A ．72B ．－72C ．36D ．－36解析：选B.∵a ·b ＝|a ||b |cos60°＝12，∴(a ＋2b )·(a －3b )＝a 2－a ·b －6b 2＝36－12－96＝－72.5．若O 是△ABC 所在平面内一点，且满足|OB →－OC →|＝|OB →＋OC →－2OA →|，则△ABC 的形状为( )A ．等腰直角三角形B ．直角三角形C ．等腰三角形D ．等边三角形解析：选B.OB →＋OC →－2OA →＝OB →－OA →＋OC →－OA →＝AB →＋AC →，OB →－OC →＝CB →＝AB →－AC →，于是|AB →＋AC →|＝|AB →－AC →|，所以|AB →＋AC →|2＝|AB →－AC →|2，即AB →·AC →＝0，从而AB ⊥AC ，故选B.6．在△ABC 中，M 是BC 的中点，AM ＝1，点P 在AM 上且满足AP →＝2PM →，则AP →·(PB→＋PC →)等于( )A.49B.43C ．－43D ．－49解析：选A.∵AM ＝1，且AP →＝2PM →.∴|AP →|＝23. 如图，AP →·(PB →＋PC →)＝AP →·2PM →＝AP →·AP →＝AP →2＝(23)2＝49. 二、填空题7．若向量a 、b 满足|a |＝|b |＝1，a 与b 的夹角为120°，则a ·a ＋a ·b ＝________. 解析：∵a ·a ＝|a ||a |cos0°＝1，a ·b ＝|a ||b |cos120°＝－12， ∴a ·a ＋a ·b ＝1－12＝12. 答案：128．若等边△ABC 的边长为23，平面内一点M 满足CM →＝16CB →＋23CA →，则MA →·MB →＝________.解析：如图，MA →·MB →＝(CA →－CM →)·(CB →－CM →)＝(CA →－16CB →－23CA →)·(CB →－16CB →－23CA →)＝(13CA →－16CB →)·(56CB →－23CA →) ＝718CA →·CB →－29CA →2－536CB →2 ＝718×(23)2×cos60°－29×(23)2－536×(23)2 ＝－2.答案：－29．(2011年烟台模拟)设a 与b 是两个向量，定义|a ×b |＝|a |·|b |·sin θ，θ是a 与b 之间的夹角，则下列说法正确的是________．①若a ＝(1，3)，b ＝(2,0)，则|a ×b |＝23；②当向量a 与b 方向相同时，|a ×b |＝0；③当向量a 与b 方向相反时，|a ×b |＝0；④|a ×b |是向量a 与b 张成的平行四边形的面积的大小．解析：①若a ＝(1，3)，b ＝(2,0)，则a 与b 的夹角为π3，∴|a ×b |＝2×2×sin π3＝2 3. ②当向量a 与b 方向相同时，|a ×b |＝|a ||b |sin0＝0.③当向量a 与b 方向相反时，|a ×b |＝|a ||b |sinπ＝0.④如图，作OA →＝a ，OB →＝b ，|b |sin θ＝|BB 1|，所以|a ×b |是向量a 与b 张成的平行四边形的面积的大小．答案：①②③④三、解答题10．已知|a |＝4，|b |＝5，|a ＋b |＝21，求：(1)a ·b ；(2)(2a －b )·(a ＋3b )．解：(1)∵|a ＋b |＝21，∴21＝a 2＋b 2＋2a ·b .又|a |＝4，|b |＝5，∴a ·b ＝21－16－252＝－10. (2)(2a －b )·(a ＋3b )＝2a 2－3b 2＋5a ·b＝2×42－3×52＋5×(－10)＝－93.11．设平面上有四个互异的点A ，B ，C ，D ，已知(DB →＋DC →－2DA →)·(AB →－AC →)＝0，试判断△ABC 的形状．解：∵(DB →＋DC →－2DA →)·(AB →－AC →)＝(DB →－DA →＋DC →－DA →)·(AB →－AC →)＝(AB →＋AC →)·(AB →－AC →)＝0，即|AB →|2－|AC →|2＝0，∴|AB →|＝|AC →|.∴△ABC 为等腰三角形．12．设△ABC 是⊙O 内接正三角形，P 是⊙O 上任一点，则P A 2＋PB 2＋PC 2是否为定值？若是正多边形，结论是否成立？解：∵P A →＝OA →－OP →，∴|P A →|2＝(OA →－OP →)2＝|OA →|2－2OA →·OP →＋|OP →|2＝2r 2－2OA →·OP →(r 为半径)．同理|PB →|2＝2r 2－2OB →·OP →，|PC →|2＝2r 2－2OC →·OP →，∴|P A →|2＋|PB →|2＋|PC →|2＝6r 2－2(OA →＋OB →＋OC →)OP →，而OA →＋OB →＋OC →＝0，∴|P A →|2＋|PB →|2＋|PC →|2＝6r 2为定值．当为正多边形时，结论仍然成立．。

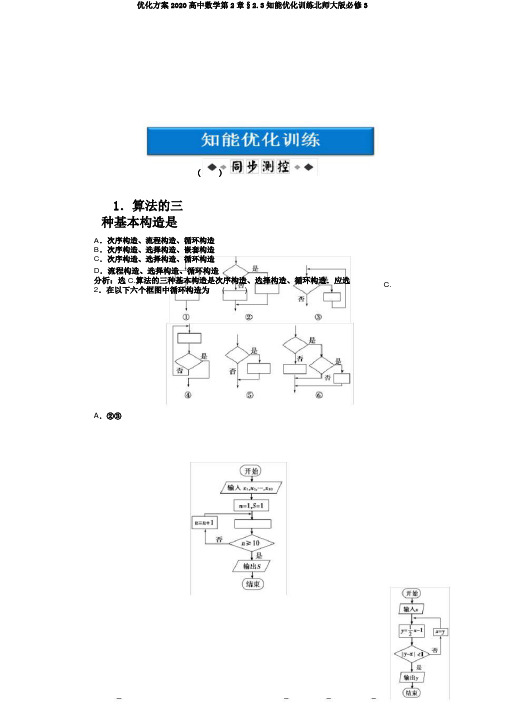
()1．算法的三种基本构造是A．次序构造、流程构造、循环构造B．次序构造、选择构造、嵌套构造C．次序构造、选择构造、循环构造D．流程构造、选择构造、循环构造分析：选C.算法的三种基本构造是次序构造、选择构造、循环构造．应选C. 2．在以下六个框图中循环构造为()A．②③B．②④C．③④D．③⑤分析：选 C.由循环构造的要求知，只有③④为循环构造，应选 C.3．(2020年高考陕西卷)如图是求x1，x2，，x10的乘积S的程序框图，图中空白框中应填入的内容为()A．S＝S*(n＋1)B．S＝S*x n＋1C．S＝S*nD．S＝S*x n分析：选D.由题意可知，输出的是10个数的乘积，故循环体应为S＝S*x n.4.(2020年高考山东卷)履行以下图的程序框图，若输入x＝4，则输出y的值为________．分析：当x＝4时，y＝1，不知足|y－x|<1，所以由x＝y知x＝1.当x＝11时，y＝－，不知足2|y－x|<1，所以由x＝y知x＝－1.当215x＝－时，y＝－，24此时，|－5＋1|<1建立，跳出循环，输出y＝－5. 424答案：－54一、选择题1．以下说法不正确的选项是()A．次序构造是由若干个挨次履行的办理步骤构成的，每一个算法都离不开次序构造B．循环构造是在一些算法中从某处开始依据必定的条件，频频履行某些办理步骤，故循环构造必定包括选择构造C．循环构造不必定包括选择构造D．用算法框图表示的算法更形象、直观，简单理解分析：选C.任何算法都是由若干个次序构造构成，循环构造中要对能否循环进行判断，所以必定包括条件构造，应选 C.2．下边的程序框图，表示的算法的功能是()A．计算小于100的奇数的连乘积B．计算从1开始的连续奇数的连乘积C．从1开始的连续奇数的连乘积，当乘积大于100时，计算奇数的个数D．计算1×3×5××n≥100时的最小的n值分析：选D.由输出框知，输出的数为奇数i，由判断框≥100知，该算法框图的功能S是计算1×3×5××n≥100时的最小的n值．3.(2020年高考浙江卷)某程序框图以下图，若输出的S＝57，则判断框内为()A．k>4B．k>5C．k>6D．k>7分析：选A.当k＝1时，k＝k＋1＝2，S＝2×1＋2＝4；当k＝2时，k＝k＋1＝3，S＝2×4＋3＝11；当k＝3时，k＝k＋1＝4，S＝2×11＋4＝26；当k＝4时，k＝k＋1＝5，S＝2×26＋5＝57.此时S＝57，循环结束，k＝5，所以判断框中应为“k>4”．4.阅读以下图的程序框图，若输出s的值为－7，则判断框内可填写()A．i<3B．i<4C．i<5D．i<6分析：选D.i＝1，s＝2；s＝2－1＝1，i＝1＋2＝3；s＝1－3＝－2，i＝3＋2＝5；s＝－2－5＝－7，i＝5＋2＝7.因输出s的值为－7，循环停止，故判断框内应填“i<6”．5．阅读以下图的程序框图，运转相应的程序，输出的i值等于()A．2B．3C．4D．5分析：选 C.当i＝1时，a＝1×2＝2，s＝0＋2＝2，i＝1＋1＝2；因为2>11不建立，2＝2＋8＝10，＝2＋1＝3；因为10>11不建立，故a3＝10故＝2×2＝8，＝3×2＝24，a s i s＋24＝34，i＝3＋1＝4；34>11建立，故输出的i＝4.6．以下图算法框图中的循环体是()A．A B．CC．ABCD D．BD分析：选D.图中C部分是给予循环变量的初始值1，预示循环开始；B和D部分是频频履行的部分，称为循环体；A部分是判断能否持续履行循环体，称为循环的停止条件，则循环体是BD.二、填空题7．按以下程序框图来计算：假如x＝5，则应当运算________次才停止．分析：输入x＝5；运算第一次，3x－2＝3×5－2＝13；运算第二次，3×13－2＝39－2＝37；运算第三次，3×37－2＝109；运算第四次，3×109－2＝325>200.结束．答案：四8.(2020年高考浙江卷)若某程序框图以下图，则该程序运转后输出的k的值是________．分析：初始值：k＝2，履行“k＝k＋1”得k＝3，a＝43＝64，b＝34＝81，a>b不建立；44k＝4，a＝4＝256，b＝4＝256，a>b不建立；k＝5，a＝45＝1024，b＝54＝625，a>b建立，此时输出k＝5.答案：59．如图是一个算法流程图，则输出的S的值是________．分析：由循环构造的流程图可得，第一次循环：S＝1＋21＝3，n＝2；第二次循环：S＝23S＝15＋24 3＋2＝7，n＝3；第三次循环：S＝7＋2＝15，n＝4；第四次循环：＝31，n＝5；第五次循环：S＝31＋25＝63，此时退出循环，输出S＝63.答案：63三、解答题10．(2020年深圳调研)给出以下10个数5,9,80,43,95,28,17,60,36,73.要求把大于的数找出来并输出，试画出该问题的算法框图．解：算法框图以下：11．设计求1＋2＋3＋4＋＋2020的一个算法，并画出相应的算法框图．解：算法以下：1．s＝02．i＝13．s＝s＋i4．i＝i＋15．假如6．输出i不大于2020，返回从头履行s的值，结束算法．3,4,5，不然履行6；则最后获得的s的值就是1＋2＋3＋4＋＋2020的值．依据以上步骤可画出以下图的程序框图．12．假设在银行存款10000元，按年利率 2.2%计算，一年后连本带息将变为10220元．若将此款所有持续存入银行，番．假设年利率不变，设计一个算法框图计算多少年会连本带利翻一解：算法框图以下：。

1．一物体做匀加速直线运动，位移方程为s ＝5t ＋2t 2，则该物体运动的初速度为______，加速度为______，2 s 内的位移大小是______．解析：由s ＝v 0t ＋12at 2作对照，则s ＝5t ＋2t 2式中，v 0＝5 m/s ，a ＝4 m/s 2. 答案：5 m/s 4 m/s 2 18 m2．图2－6－2是甲、乙两物体的位移和速度图象，则甲物体在前2 s 内的位移是______m,5 s 内的总位移是______m ，乙物体在前2 s 内的位移是________m,5 s 内的总位移是______m.图2－6－2 答案：2 －2 6 163．电梯从一楼开始以加速度a 匀加速上升，速度达到v 后，匀速上升一段时间，再以大小为a 的加速度做匀减速运动，到30层楼停止运动.30层楼高h ，则电梯匀速运动时间为____________，电梯完成上述运动总的时间为______．解析：设匀加速运动时间为t 1，位移为h 1，匀速运动时间为t 2，位移为h 2，匀减速时间为t 3，位移为h 3，总时间为t ，规定电梯运行方向为正方向．t 1＝v a .h 1＝12at 21＝v 22a .t 3＝0－v －a ＝v a .h 3＝v t 3＝v 2·v a ＝v 22a.所以h 2＝h －h 1－h 3＝h －v 2a .t 2＝h 2v ＝h v －v a t ＝t 1＋t 2＋t 3＝v a ＋h v －v a ＋v a ＝v a ＋h v. 答案：h v －v a v a ＋h v 4．一辆满载乘客的飞机由于某种原因紧急着陆，着陆时的加速度大小为6 m/s 2，着陆前的速度为60 m/s ，求：(1)飞机着陆后5 s 末的瞬时速度；(2)飞机着陆后12 s 内滑行的距离．答案：(1)30 m/s (2)300 m1．几个做匀变速直线运动的物体，在t s 内位移最大的是( )A ．加速度最大的物体B ．初速度最大的物体C ．末速度最大的物体D ．平均速度最大的物体解析：选D.s ＝v t .2．关于平均速度v ＝v 0＋v t 2，下列说法中正确的是( ) A ．只适用于匀加速直线运动B ．只适用于匀减速直线运动C ．适用于匀变速直线运动D ．非匀变速运动也适用答案：C3．一小球沿斜面以恒定的加速度滚下并依次通过A 、B 、C 三点，已知AB ＝6 m ，BC ＝10m ，小球通过AB 、BC 所用的时间均为2 s ，则小球经过A 、B 、C 三点时的速度分别为( )A ．2 m/s,3 m/s,4 m/sB ．2 m/s,4 m/s,6 m/sC ．3 m/s,4 m/s,5 m/sD ．3 m/s,5 m/s,7 m/s解析：选B.如图所示，T ＝2 s ，Δs ＝10－6＝4(m)， a ＝Δs T 2＝44＝1(m/s 2)． v B 为中间时刻，v B ＝10＋62T ＝164＝4(m/s)． Δv ＝a Δt ＝aT ＝2 m/s.v A ＝v B －Δv ＝(4－2) m/s ＝2 m/sv C ＝v B ＋Δv ＝(4＋2) m/s ＝6 m/s.4．一质点做直线运动，当时间t ＝t 0时，位移s >0，速度v >0，其加速度a >0，此后a 逐渐减小，则它的( )A ．速度逐渐减小B ．位移始终为正值，速度变为负值C ．速度的变化越来越慢D ．位移的变化越来越慢 解析：选C.t ＝t 0时刻，有s ＝s 0＋v 0t ＋122，v t ＝v 0＋at .加速度是描述速度变化快慢的物理量．5．做匀减速直线运动的物体，它的加速度大小为a ，初速度大小是v 0，经过时间t 速度减小到零，则它在这段时间内的位移大小表达错误的式子是( )A ．v 0t ＋12at 2B ．v 0t －12at 2 C.v 02t D.12at 2 解析：选A.⎩⎪⎨⎪⎧ s ＝v 0t －12at 2v 0＝at⇒ ⎩⎨⎧s ＝v 20a －12·v 20a ＝12·v 20a ＝122s ＝v t ＝v 02t ＝v 202a6．一物体做匀加速直线运动，在某时刻之前t 1 s 内位移为s 1，在该时刻后t 2 s 内的位移为s 2，则该物体的加速度为( )A.2(s 2t 1－s 1t 2)t 1t 2(t 1＋t 2)B.s 2t 1－s 1t 2t 1t 2(t 1＋t 2)C.2(s 1t 2－s 2t 1)t 1t 2(t 1＋t 2)D.s 1t 2－s 2t 1t 1t 2(t 1＋t 2)解析：选A.利用匀变速直线运动的规律求解． s 1段中间时刻的速度为v t 12＝s 1t 1； s 2段中间时刻的速度v t 22s 2t 2，这两时刻的时间间隔为t 12＋t 22＝12(t 1＋t 2)． 由于物体做匀加速直线运动，由加速度定义可得 a ＝v t 22－v t 1212(t 1＋t 2)＝s 2t 2－s 1t 112(t 1＋t 2)＝2(s 2t 1－s 1t 2)t 1t 2(t 1＋t 2). 7．(1)物体的初速度为2 m/s ，加速度为2 m/s 2，当它的速度增加到6 m/s 时，所通过的路程s ＝______.(2)某物体的初速度为2 m/s ，用4 s 的时间速度增加到6 m/s 时，那么该物体在这段时间内发生的位移为______．(3)飞机着陆后在跑道上做匀减速直线运动，已知初速度是60 m/s ，加速度大小是6 m/s 2，则飞机着陆后12 s 内的位移是______．解析： v 2t －v 20＝2as .第(3)小题中，10 s 末速度减为零．s ＝60×10－12×6×102＝300(m)． 答案：(1)8 m (2)16 m (3)300 m8．一质点做匀加速直线运动，第2 s 内的位移为6.5 m ，第6 s 内的位移为18.5 m ，求质点的加速度．解析：因为1.5 s 末和5.5 s 末正好是第2 s 和第6 s 的中间时刻，则有v 1.5＝6.5 m/sv 5.5＝18.5 m/s由加速度定义有a ＝v 5.5－v 1.55.5－1.5＝18.5－6.54m/s 2＝3 m/s 2. 答案：3 m/s 29．骑自行车的人以5.0 m/s 的初速度匀减速上一个斜坡，加速度大小是0.4 m/s 2，斜坡长为30 m ，骑自行车的人通过斜坡要多长时间？解析：设减速到零所用时间为t 0，有0＝5－0.4t 0，t 0＝12.5 s在此时间内的位移s ＝5×12.5－12×0.4×12.52＝31.25 m>30 m ．即能够通过斜坡． 由s ＝v 0t ＋12at 2，式中s ＝30 m ，v 0＝5 m/s ，a ＝－0.4 m/s 2.代入即得t ＝10 s, t <12.5 s. 答案：10 s10．高速公路给人们出行带来了方便，但是因为在高速公路上行驶的车辆速度大，雾天往往出现十几辆车追尾连续相撞的车祸．汽车在沪宁高速公路上正常行驶速率为120 km/h ，汽车刹车产生的最大加速度为8 m/s 2，大雾天关闭高速公路，如果某天有薄雾，能见度约为40 m ，为安全行驶，避免追尾连续相撞，汽车行驶速度应如何限制？(设司机反应时间为0.6 s)．解析：在司机反应时间t 1内，汽车以恒定速度行驶，然后司机刹车，汽车做匀减速运动，直到停止．两个过程中汽车的位移之和不能超过40 m ．设汽车行驶速度为v 时，从司机发现前方物体到汽车停下来，汽车的位移刚好为40 m ，则在反应时间内汽车位移s 1＝v t 1＝v ×0.6 s ．汽车的速度从v 减小到零的时间t 2＝v t －v a ＝－v －8 m/s 2＝v 8 m/s 2，匀减速位移s 2＝v ＋02·t 2＝v 216 m/s ，则s 1＋s 2＝40 m ，即v 0.6 s ＋v 216 m/s ＝40 m ．v ≈21 m/s ＝75.6 km/h.所以汽车的行驶速度应小于75.6 km/h.答案：小于75.6 km/h。

一、基础知识1．下列词语中加点字的注音,全都正确的一项是（）A．倡．（chānɡ)女憔．（jiāo)悴六幺．（yāo)B．铮铮．（zhēnɡ）贾．(jiǎ）人荻．（dí)花C．嘈．(cáo)杂虾．（há)蟆钿．(diàn）头D．浸．（qìn)水呕哑．(yā）嘲哳．(zhā）解析：选C。

A项“憔”应读qiáo，B项“贾”应读ɡǔ，D项“浸"应读jìn.2．下列各句中加点的词语解释不．正确的一组是（)A．使快．弹数曲快：畅快,尽情东船西舫悄无言．言:说话B．凝绝不通声暂．歇暂：暂时，短暂转轴拨．弦三两声拨：拨动C．满座重闻皆掩泣．泣：哭泣曲终收拨．当心画拨:拨子D．莫辞．更坐弹一曲辞：推辞转．徙于江湖间转：辗转解析:选A.言:说话的声音。

3．下列句子中加点词的用法不．同的一项是( )A．歌．以赠之楚人一炬，可怜焦土．．B．梦．啼妆泪红阑干君子博学而日．参省乎己C．商人重．利轻．别离简能．而任之D．外连衡而斗．诸侯若亡．郑而有益于君，敢以烦执事解析：选C.“重"“轻”,形容词活用作动词，“重视”、“轻视”；“能"，形容词活用作名词，“有才能的人”.A项中均为名词活用作动词;B项中均为名词作状语;D项中均为动词的使动用法。

4．下列句子中加点词不．是古今异义的一项是（）千里，百二十城A．今齐地方．．暮去朝来颜色故．．长句，歌以赠之B．因为．．传道受业解惑也师者，所以．．C．失向来之烟霞．．凄凄不似向前声．．D．世间行乐亦如此．．自安予出官二年，恬然．．解析：选D。

“行乐”:消遣，取乐,古今同义；“恬然”：淡泊宁静的样子，古今同义。

A项中“地方”，古义:土地方圆；今义:泛指空间的一部分。

“颜色"，古义：容貌;今义：由物体发射、反射或透过的光波通过视觉所产生的印象。

B项中“因为”,古义：于是创作；今义：①介词,表示原因;②连词,常跟“所以”连用，表示因果关系。

专题十五议论文阅读知能优化训练中考回顾一、(2022河南)阅读下面的文字,完成后面的题目。

文本一谈青年的责任担当张建林①李大钊先生说过:“青年者,国家之魂。

”青年是国家未来的主人,理应担当起国家富强、民族复兴的重任。

②青年要担当,就要树立崇高的理想信念。

古人云,志不立,天下无可成之事。

青年处于人生的“拔节孕穗期”,理想信念是青年成长发展的精神动力。

马克思青年时就立志为人类的解放事业而工作,并用一生来践行,正是这样的崇高理想成就了他的伟大事业。

青年最有朝气,最肯学习,最具有创造未来的能力,早一点树立崇高的理想信念,就能早一点明确人生的方向,正如一首诗所写的那样:“理想是火,点燃希望的灯;理想是灯,照亮前行的路。

”青年只有树立崇高理想,才能获得动力,激发潜能,“以青春之我,创建青春之家庭,青春之国家,青春之民族,青春之人类,青春之地球,青春之宇宙”。

③青年要担当,就要有深厚的爱国情怀。

爱国情怀能使人将个人的发展与国家的命运紧密相连。

鲁迅先生便是在爱国情怀的指引下不断寻找救国道路的。

他最初为实业救国而学洋务,转而为寻求救国道路远赴日本学医,后来意识到精神上的“愚弱”远比身体上的疾病更需要“疗救”,就弃医从文,用笔唤醒无数麻木的灵魂。

“天下兴亡,匹夫有责”,青年作为社会的中坚力量,应把人生理想融入国家和民族的事业中,自觉地以爱国之情深化爱国之行,与时代同步伐,与祖国共命运,唯其如此,才能担当重任。

④青年要担当,就要锤炼过硬本领。

“责重山岳,能者方可为之。

”担当需要本领,本领源自学习。

青春年华是学习的大好时光,青年要学以立德、学以增智、学以明道,知行合一,探求真学问,锤炼真本领。

中国核潜艇之父彭士禄青少年时就立志向学,虽历经磨难,始终勤学不辍,刻苦钻研,将理论与实践相结合,为中国核动力的研究设计做出了开创性贡献。

现在的中国青年处于好时代,读书资源丰富,环境优越,更应珍惜学习条件,勤奋学习,增长本领,为青春远航蓄力。

1．已知l ⊥α，则过l 与α垂直的平面( )A ．有1个B ．有2个C ．有无数个D ．不存在答案：C2．下列命题：①两个相交平面组成的图形叫做二面角；②异面直线a 、b 分别和一个二面角的两个面垂直，则a 、b 所成的角与这个二面角的平面角相等或互补；③二面角的平面角是从棱上一点出发，分别在两个面内作射线所成角的最小角； ④二面角的大小与其平面角的顶点在棱上的位置没有关系．其中正确的是( )A ．①③B ．②④C ．③④D ．①②解析：选 C.①错，两个半平面形成的图形；②错，异面直线所成的角不是钝角，③④正确．3．如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，则这两个二面角的大小关系是( )A ．相等B ．互补C ．相等或互补D ．大小不确定解析：选D.如果两个二面角的棱不平行，其大小没关系．4．正方体ABCD －A 1B 1C 1D 1中，截面A 1BD 与底面ABCD 所成二面角A 1－BD －A 的正切值等于________．解析：连结AC ，交BD 于点O ，连结A 1O ，A 1C 1.∵AC ⊥BD ，BD ⊥AA 1，则BD ⊥面ACC 1A 1，∴∠A 1OA 为A 1－BD －A 的平面角．AO ＝22AA 1， ∴tan ∠A 1OA ＝A 1A AO ＝ 2. 答案： 2一、选择题1．经过平面α外一点和平面α内一点与平面α垂直的平面有( )A ．0个B ．1个C ．无数个D ．1个或无数个解析：选D.若两点连线垂直于平面有无数个，否则只有一个．2．在二面角α－l －β的棱l 上任选一点O ，若∠AOB 是二面角α－l －β的平面角，则必须具有条件( )A ．AO ⊥BO ，AO ⊂α，BO ⊂βB ．AO ⊥l ，BO ⊥lC．AB⊥l，AO⊂α，BO⊂βD．AO⊥l，BO⊥l且AO⊂α，BO⊂β解析：选D.根据二面角平面角定义可得D.3．如果一个二面角的两个半平面分别平行于另一个二面角的两个半平面，则这两个二面角的关系是()A．相等B．互补C．相等或互补D．不能确定解析：选 C.当这两个二面角的两个面均同向或均异向时，它们相等；当这两个二面角的两个面中，一组同向，另一组异向时，它们互补．4．下列说法错误的是()A．过二面角的棱上某一特殊点，分别在两个半平面内引垂直于棱的射线，则这两条射线所成的角即为二面角的平面角B．和二面角的棱垂直的平面与二面角的两个半平面的交线所成的角即为二面角的平面角C．在二面角的一个面内引棱的垂线，该垂线与其在另一面内的射影所成的角是二面角的平面角D．二面角的平面角可以是一个锐角、一个直角或一个钝角解析：选C.因为按C中所给的方法，当二面角是一个锐角时，得到的确实是二面角的平面角；但当二面角是一个直二面角时，得到的是一个零度角；当二面角是一个钝角时，得到的是二面角平面角的一个补角．即C中方法不具有普遍适用性．5．自二面角内任意一点分别向两个面引垂线，则两垂线所成的角与二面角的平面角的关系是()A．相等B．互补C．互余D．无法确定解析：选B.如图，BD，CD为AB，AC所在平面与α，β的交线，则∠BDC为二面角α－l－β的平面角．且∠ABD＝∠ACD＝90°，∴∠A＋∠BDC＝180°.6．在正四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，则下面四个结论中不成立的是()A．BC∥平面PDFB．DF⊥平面PAEC．平面PDF⊥平面ABCD．平面PAE⊥平面ABC解析：选C.可画出对应图形(图略)，则BC∥DF，又DF⊂平面PDF，BC⊄平面PDF，∴BC∥平面PDF，故A成立；由AE⊥BC，BC∥DF，知DF⊥AE，DF⊥PE，∴DF⊥平面PAE，故B成立；又DF⊂平面ABC，∴平面ABC⊥平面PAE，故D成立．二、填空题7.如图，把直角三角形ABC沿斜边上的高CD折成直二面角A－CD－B后，互相垂直的平面有______对．解析：面ADC⊥面ABD，面BDC⊥面ABD，面ADC⊥面BDC.答案：38．已知m、l是直线，α、β是平面，给出下列说法：①若l垂直于α内两条相交直线，则l⊥α；②m⊂α，l⊂β，且l⊥m，则α⊥β；③若l⊂β，且l⊥α，则α⊥β；④若m⊂α，l⊂β，则α∥β，则l∥m.其中正确的序号是________．解析：①③符合线⊥面，面⊥面的判定定理，②错，并没有得出α⊥β；③错，l与m可以异面．答案：①③9．若二面角α－l－β的平面角是锐角，点P到α、β和棱l的距离分别为22、4和42，则二面角的大小为________．解析：如图(1)，(2)．PA⊥β于A点，PB⊥α于B点．PA、PB的平面与l交于点C，则∠ACB为α－l－β的平面角．在(1)中，P在α－l－β内，可得∠ACB＝∠ACP＋∠PCB＝45°＋30°＝75°.在(2)中，P在α－l－β外，可得∠ACB＝∠ACP－∠PCB＝45°－30°＝15°.答案：15°或75°三、解答题10．如图，在空间四边形ABCD中，AB＝BC，CD＝DA，E、F、G分别为CD、DA和对角线AC的中点．求证：平面BEF⊥平面BGD.证明：∵AB＝BC，CD＝DA，G是AC的中点，∴BG ⊥AC ，DG ⊥AC ，∴AC ⊥平面BGD .又EF ∥AC ，∴EF ⊥平面BGD .∵EF ⊂平面BEF ，∴平面BEF ⊥平面BGD .11．(2010年高考辽宁卷节选)如图，棱柱ABC －A 1B 1C 1的侧面BCC 1B 1是菱形，B 1C ⊥A 1B .证明：平面AB 1C ⊥平面A 1BC 1.证明：∵侧面BCC 1B 1是菱形，∴B 1C ⊥BC 1，又已知B 1C ⊥A 1B ，且A 1B ∩BC 1＝B ，∴B 1C ⊥平面A 1BC 1.又B 1C ⊂平面AB 1C ，∴平面AB 1C ⊥平面A 1BC 1.12．如图，在正方体ABCD －A 1B 1C 1D 1中，求二面角B －A 1C 1－B 1的正切值． 解： 取A1C 1的中点O ，连结B 1O ，BO . 由题意知B 1O ⊥A 1C 1，又BA 1＝BC 1，O 为A 1C 1的中点，所以BO ⊥A 1C 1，所以∠BOB 1即是二面角B －A 1C 1－B 1的平面角．因为BB 1⊥平面A 1B 1C 1D 1，OB 1⊂平面A 1B 1C 1D 1， 所以BB 1⊥OB 1.设正方体的棱长为a ，则OB 1＝22a ，在Rt △BB 1O 中， tan ∠BOB 1＝BB 1OB 1＝a 22a ＝2， 所以二面角B －A 1C 1－B 1的正切值为 2.。