数列极限存在的条件

数列的极限与边界数列是数学中的一个重要概念，它由按照一定规律排列的一系列数字组成。

数列的极限与边界是数列在逼近终点时所遵循的规律与限制。

本文将探讨数列的极限与边界。

一、数列的极限数列的极限是指当数列的项无限逼近某个值时，该值被称为数列的极限。

数学符号表示为liman=n→∞。

1. 无穷大与无穷小在数列中，当数列的项无限逼近正无穷或负无穷时，我们称之为无穷大。

而当数列的项无限逼近零时，我们称之为无穷小。

2. 极限的存在性数列的极限并不总是存在，有些数列的极限是不存在的。

存在极限的数列被称为收敛数列，不存在极限的数列被称为发散数列。

3. 收敛数列的性质收敛数列具有以下性质：- 收敛数列的极限是唯一的；- 若数列{an}与{bn}分别收敛于a和b，则{an+bn}也收敛，并且其极限为a+b；- 若数列{an}收敛于a，且对于每一个n，有an≤bn≤cn，则数列{bn}和{cn}也收敛，并且它们的极限都是a。

二、数列的边界数列的边界是指数列的项在有限范围内所能够达到的上下限。

在数列中，存在上确界和下确界。

上确界是指数列的项中最大的一个值，而下确界是指数列的项中最小的一个值。

1. 上确界的定义对于数列{an}，如果存在一个实数M，使得对于任意的n，都有an≤M成立，那么M就是该数列的上确界。

2. 下确界的定义对于数列{an}，如果存在一个实数m，使得对于任意的n，都有an≥m成立，那么m就是该数列的下确界。

3. 数列的有界性如果数列既有上确界，又有下确界时，我们称该数列是有界的；如果不存在上确界或下确界，则该数列是无界的。

三、数列的极限与边界的关系数列的极限与边界是数列的内在联系。

在数列中，若数列的极限存在，则该数列必定是有界的，即存在上确界和下确界。

1. 极限与上确界的关系对于收敛数列{an}，当其极限存在时，该极限即为该数列的上确界。

2. 极限与下确界的关系对于收敛数列{an}，当其极限存在时，该极限即为该数列的下确界。

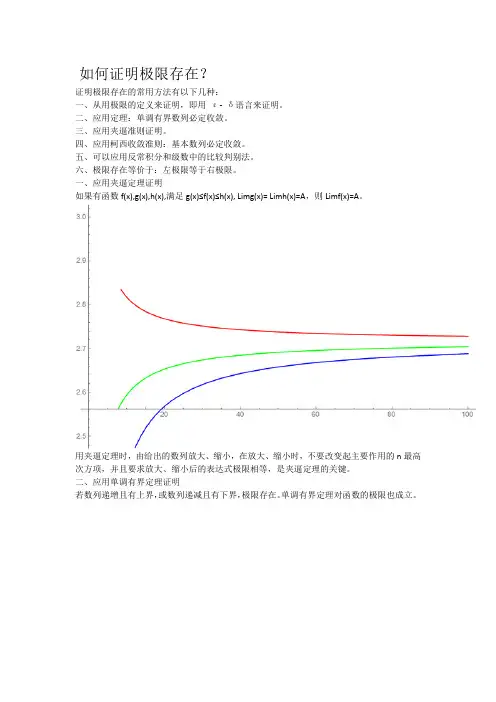
如何证明极限存在？
证明极限存在的常用方法有以下几种：
一、从用极限的定义来证明，即用ε- δ语言来证明。

二、应用定理：单调有界数列必定收敛。

三、应用夹逼准则证明。

四、应用柯西收敛准则：基本数列必定收敛。

五、可以应用反常积分和级数中的比较判别法。

六、极限存在等价于：左极限等于右极限。

一、应用夹逼定理证明
如果有函数f(x),g(x),h(x),满足g(x)≤f(x)≤h(x), Limg(x)= Limh(x)=A，则Limf(x)=A。

用夹逼定理时，由给出的数列放大、缩小，在放大、缩小时，不要改变起主要作用的n最高次方项，并且要求放大、缩小后的表达式极限相等，是夹逼定理的关键。

二、应用单调有界定理证明
若数列递增且有上界，或数列递减且有下界，极限存在。

单调有界定理对函数的极限也成立。

三、从用极限的定义入手来证明
以数列为例，设{xn}为一个无穷实数数列的集合。

如果存在实数a，对于任意正数ε （不论其多么小），都N>0，使不等式|xn-a|<ε在n∈(N,+∞)上恒成立，那么就称常数a是数列{xn} 的极限。

四、应用极限存在的充要条件证明
即函数左极限等于右极限，数列奇子列极限等于偶子列极限。

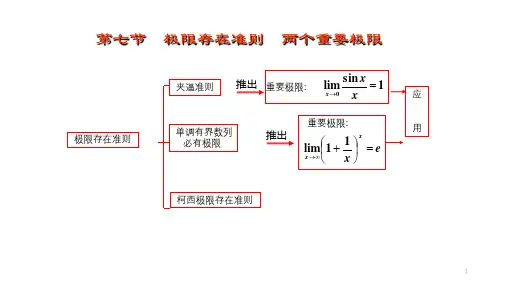
极限存在两个准则
数列极限存在的两个定理
1、 夹逼定理：
若∃N ，当n>N 时，≤≤
n y n x n z 存在条件A y n n =∞→lim =A z n n =∞
→lim ，则：
A x
n n =∞→lim 2、 单调有界数列必收敛定理：
单调上升数列有上界
收敛
单调下降有下界
收敛
函数极限存在的两个定理：
1、 夹逼定理：
存在∃δ>0,在δ<−<0x x 0时，有
n y ≤≤，
n x n z 存在条件A y n x x =→0x x →0
x x → 则：
x lim =，则： A z n =lim A x
n x x =→lim 0
其他趋近过程也有类似结论 2、 单侧极限与双侧极限的关系: A x f =)(lim 0
A x f =−0
0 0 h(x)
0<x<0+δ 只能分别求两侧极限。

3、 一元函数极限不存在时常用的两种方法：
① 左右侧极限存在，但是不相等
)( x -δ<x<
x x x
求极限时，指数函数 y=
x a 反正切函数y=arctanx 反余切函数
y=arccotx 必须要求两侧的极限值。

② ⅰ、∃
→，≠； n x 0x n x 0x
不存在， )(lim n
n x f +∞→ⅱ、∃→，→，
n x 0x n y 0x 但是≠ )(lim n n x f +∞→)(lim n n y f +∞→。

第二章数列极限2 数列极限存在的条件若数列{a n}的各项满足a n≤a n+1(a n≥a n+1)，则称{a n}为递增(递减)数列。

递增数列和递减数列统称为单调数列。

定理 2.9(单调有界定理)：在实数系中，有界的单调数列必有极限，且其极限就是它的上(下)确界.证：若{a n}为有上界的递增数列. 由确界原理可知，{a n}有上确界，记a=sup {a n}. 则对∀ε>0，有{a n}中的某一项a N，使得a-ε<a N.∵{a n}递增，∴当n≥N时，有a-ε<a N≤a n.又{a n}有上界，∴对一切a n，都有a n≤a<a+ε.综上，当n≥N时，有a-ε<a n <a+ε, ∴=a.若{a n}为有下界的递减数列. 由确界原理可知，{a n}有下确界，记b=inf {a n}. 则对∀ε>0，有{a n}中的某一项a N，使得b+ε>a N.∵{a n}递减，∴当n≥N时，有b+ε>a N≥a n.又{a n}有下界，∴对一切a n，都有a n≥b>b-ε.综上，当n≥N时，有b-ε>a n >b+ε, ∴=b.例1：设a n=1，n=1,2,…，其中实数a≥2. 证明数列{a n}收敛. 证：∵a n-1-a n=(1)- (1)=>0.∴{a n}递增. 又a n≤1≤1=2<2，n=1,2,…，∴{a n}有上界. 由单调有界定理可知{a n}收敛.例2：证明数列,,……收敛，并求其极限.n个根号证：记a n=，且a1=<2, 可设a n<2，则有a n+1=<<2，从而对一切n，有a n<2，即{a n}有界。

又a1=>0，a2=>=a1>0，可设a n>a n-1，即a n-a n-1>0；则a n+1-a n=>0，∴{a n}递增.由单调有界定理可知，数列{a n}有极限，记为a. 由=2+a n，对两边取极限得a2=2+a，解得a= -1或a=2. 由数列极限的保不等式性知，a= -1不合理，舍去. ∴.例3：设S为有界数集. 证明：若sup S=a∉ S，则存在严格递增数列{x n}⊂S，使得=a.证：∵sup S=a，∴∀ε>0，∃x∈S，使x>a-ε. 又a∉ S，∴x<a，从而有a-ε< x<a，取ε1=1，则∃x1∈S，使得a-ε1< x1<a，再取ε2=min{,a- x1}>0，则∃x2∈S，使得a-ε2< x2<a，且有x2> a-ε2≥a-(a- x1)= x1.如上循环进行可得x n-1∈S，取εn=min{,a- x n-1}>0，则∃x n∈S，使得a-εn< x n<a，且有x n> a-ε2≥a-(a- x n-1)= x n-1. 至此得到严格递增数列{x n}⊂S，且满足a-εn< x n<a<a+εn，∴=a.例4：证明存在.证：建立不等式b>a>0，对任一正整数n有，b n+1-a n+1<(n+1)b n(b-a)，即a n+1> b n[(n+1)a-nb] (1)以a=1，b=1代入(1)式，得，∴递增；再以a=1，b=1代入(1)式，得1>=，∴<4.∴有界；根据单调有界定理可知：收敛。

§2.3 数列极限存在的条件教案内容：第二章 数列极限 ——§2.3 数列极限存在的条件 教案目标：使学生掌握判断数列极限存在的常用工具.教案要求：(1) 掌握并会证明单调有界定理，并会运用它求某些收敛数列的极限；(2) 初步理解Cauchy 准则在极限理论中的主要意义，并逐步会应用Cauchy 准则判断某些数列的敛散性.教案重点：单调有界定理、Cauchy 收敛准则及其应用. 教案难点：相关定理的应用. 教案方法：讲练结合. 教案过程： 引言在研究比较复杂的极限问题时，通常分两步来解决：先判断该数列是否有极限（极限的存在性问题）；若有极限，再考虑如何计算些极限（极限值的计算问题）.这是极限理论的两基本问题.在实际应用中，解决了数列{}n a 极限的存在性问题之后，即使极限值的计算较为困难，但由于当n 充分大时，n a 能充分接近其极限a ，故可用n a 作为a 的近似值.本节将重点讨论极限的存在性问题.为了确定某个数列是否有极限，当然不可能将每一个实数依定义一一加以验证，根本的办法是直接从数列本身的特征来作出判断.从收敛数列的有界性可知：若{}n a 收敛，则{}n a 为有界数列；但反之不一定对，即{}n a 有界不足以保证{}n a 收敛.例如{}(1)n -.但直观看来，若{}n a 有界，又{}n a 随n 的增大（减少）而增大（减少），它就有可能与其上界（或下界）非常接近，从而有可能存在极限（或收敛）.为了说明这一点，先给出具有上述特征的数列一个名称——单调数列. 一、单调数列定义 若数列{}n a 的各项满足不等式11()n n n a a a a ++≤≥，则称{}n a 为递增（递减）数列.递增和递减数列统称为单调数列．例如：1n ⎧⎫⎨⎬⎩⎭为递减数列；{}2n 为递增数列；(1)n n ⎧⎫-⎨⎬⎩⎭不是单调数列.二、单调有界定理问题 （1）单调数列一定收敛吗？；（2）收敛数列一定单调吗？一个数列{}n a ，如果仅是单调的或有界的，不足以保证其收敛，但若既单调又有界，就可以了.此即下面的极限存在的判断方法.定理（单调有界定理） 在实数系中，有界且单调数列必有极限. 几何解释 单调数列}{n a 只可能向一个方向移动，故仅有两种可能：（1）点na 沿数轴移向无穷远；（2）na 无限趋于某一个定点A ，即)(∞→→n A a n .证明 不妨设}{n a 单调增加有上界，把}{n a 看作集合，有确界原理，μ=}sup{n a 存在即：（1）n ∀，μ≤n a ；（2）0>∀ε，N n ∈∃0使0n a εμ->,由于}{n a 单调增加，故当0n n >时有εμ-<0n a εμμ+<≤≤n a即当n n >时εμ<-||n a 亦即μ=∞→n n a lim .例10>a ，证明数列a a =1，a a a +=2，a a a a ++=3，……，n a a=++，……收敛，并求其极限.证明 从该数列的构造，显见它是单调增加的，下面来证它是有界的.易见0>≥a a n ，且12a a a +=，23a a a +=，…，1-+=n n a a a ，…,从而12-+=n n a a a na a +< 两端除以na 得nn a aa +<1,n ∀，a a n ≥ ⇒ a a a n +<≤1 故}{n a 有界即得极限存在.设∞→n lim l a n=，对等式12-+=n n a a a 两边取极限，则有)(lim lim 12-∞→∞→+=n n n n a a a =aa n n +-∞→1lim ⇒al l +=22411al +±=⇒,因}{n a 为正数列，故0≥l ，因此取2411al ++=即为所求极限.例2 求∞→n lim nka n （k 为一定数，1>a ）解 记=n c n ka n ，则0>n c 且kk n n n a n n a c c )11(1)1(11+=+=+1>a ，则N ∃，当N n >时1)11(1<+k n a ，故N n >后，}{n c 单调递减，又有0>n c ⇒极限一定存在，设为A ,由n k n c n a c )11(11+=+两边取极限得A a A 1=（1>a ）0=⇒A . 例3 设 ). 2 ( ,131211≥++++=ααααna n 证明数列{n a }收敛. 例4.21 .0 ,011⎪⎪⎭⎫⎝⎛+=>>+n n n x a x x x a 求.lim n n x ∞→ ( 计算a 的逐次逼近法, 亦即迭代法 ). 解 由均值不等式, 有⎪⎪⎭⎫ ⎝⎛+=+n n n x a x x 21 1}{ .n nn x a x ax ⇒=⋅≥有下界,注意到对,n ∀有,a x n ≥有nn n n x a a x a x x .1) (121121221⇒=⎪⎪⎭⎫ ⎝⎛+≤⎪⎪⎭⎫ ⎝⎛+=+↘，,.lim a x n n =∞→三、柯西收敛准则 (一) 引言单调有界定理只是数列收敛的充分条件，下面给出在实数集中数列收敛的充分必要条件——柯西收敛准则. (二) Cauchy 收敛准则定理（Ｃauchy 收敛准则） 数列{}n a 收敛的充分必要条件是：对任给的0ε>，存在正整数Ｎ，使得当,n m N >时有||n m a a ε-<.证明“⇒”}{n a 收敛，则存在极限，设a a n n =∞→lim ，则0>∀ε，N ∃，当N n >时有2/||ε<-a a n ⇒当N m n >,时有ε<-+-≤-||||||a a a a a a n m m n“⇐”先证有界性，取1=ε，则N ∃，N m n >,⇒1||<-m n a a .特别地，N n >时1||1<-+N n a a ⇒1||||1+<+N n a a ,设}1|||,|,|,||,m ax {|121+=+N N a a a a M ，则n ∀，Ma n ≤||.再由致密性定理知，}{n a 有收敛子列}{k n a ，设aa k n k =∞→lim ,0>∀ε，1N ∃，1,N m n >⇒||/2n m a a ε-<,K ∃，K k >⇒2/||ε<-a a k n ,取),m ax (1N K N =，当N n >时有11N n N N +≥+>⇒ εεε=+<-+-≤-++2/2/||||||11a a a a a a N N n n n n ,故a a n k =∞→limCauchy 列、基本列（满足Cauchy 收敛准则的数列） Cauchy 收敛准则的另一表示形式：0>∀ε，N ∃，当N n >时，对P +∀∈=Z 有ε<-+||n P n a a .(三) 说明1、auchy 收敛准则从理论上完全解决了数列极限的存在性问题.2、auchy 收敛准则的条件称为Ｃauchy 条件，它反映这样的事实：收敛数列各项的值愈到后面，彼此愈接近，以至于充分后面的任何两项之差的绝对值可以小于预先给定的任意小正数.或者，形象地说，收敛数列的各项越到后面越是“挤”在一起.3、auchy 准则把N ε-定义中n a 与a 的之差换成n a 与m a 之差.其好处在于无需借助数列以外的数a ，只要根据数列本身的特征就可以鉴别其（收）敛（发）散性.例 如数列}{n a 满足||||11-+-≤-n n n n a a q a a （ ,3,2=n ）且10<<q ，证明数列}{n a 收敛.证明 令0||12>=-c x x ，||||11-+-≤-n n n n a a q a a 211221||||n n n q a a q x x ---≤-≤≤-||||||||1211n n p n p n p n p n n p n a a a a a a a a -++-+-≤-⇒+-+-+-+++)(132--+-++++≤n p n p n q q q c )1(11--+++=p n q q cqq q cn -≤-11. 0>∀ε，（不妨设q c-<<10ε），取]ln )1ln(1[q c qN ε-+=，则当N n >时，对任给自然数p 有ε<-<--+q cq a a n n pn 1||1.故由Cauchy 收敛准则知数列}{n x 收敛.例 证明数列n a n 1211+++= 发散.证明 要证：0>∃ε，对N ∀，必有Nm >0，0n N>使得||00ε≥-n m a a设n m >则)(1211112111||n m n n n m n n a a n m -++++++=+++++=-m nm n m m m m -=-=+++>1111 ，因此，如n m 2=，则||11/21/2m n a a -≥-=.这样，对2/10=ε，不管N 多大，如取10+=N n ，002n m =则N m >0，0n N>且212111||0000=-=-≥-m n a a n m ，这说明}{n a 不是一个Cauchy 数列.（四） 应用例5 证明: 任一无限十进小数 )10( .021<<=αα n b b b 的不足近似值所组成的数列,101010 , ,1010 ,102212211 n n b bb b b b ++++ 收敛. 其中) 9,,2,1 ( =i b i 是9,,1,0 中的数.证明 令 =n a ,101010 221n n b bb +++ 有⎪⎭⎫⎝⎛+++≤+++=--++++++++1122111011011109101010 p n p n p n n n n n n pn b b b a a1109+=n ().1101)1.0(11011.01)1.0(1n n p n p<<-=--…… 例6 设 .sin sin sin ,102n n n q q q q q q x q +++=<< 试证明数列{}n x 收敛.关于极限1lim 1nn e n →∞⎛⎫+= ⎪⎝⎭) 71828.2 (≈e 的 证明留在下节进行.例7 .11lim ,11lim knn kn n n n ⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛+∞→+∞→例8 .211lim ,11lim ,1lim 3nn nn kn n n n n c ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛+∞→∞→+∞→例9.1232lim n n n n ⎪⎭⎫⎝⎛+-∞→作业 教材P38—39 1，3，5，6，10，11；教材P40—41 1（1）（3），3，4(1)-(3)(6)(8)，5，10.（P38 3（4）提示：考虑,1nn a b =用双逼原理可求得,1→n b ）附 数列⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛+nn 11单调有界证法欣赏:Cauchy (1789—1857 ) 最先给出这一极限，Riemann （1826—1866）最先给出以下证法一.证法一 （ Riemann 最先给出这一证法 ） 设 .11nn n x ⎪⎭⎫⎝⎛+=应用二项式展开，得+⋅+=n n x n 11++⋅--+⋅- 321!3)2)(1(1!2)1(n n n n n n n n nn n n 1!123)1(⋅⋅⋅- ⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-++=n n n n n n n n 112111!12111!3111!2111 ， !21111++=+n x +⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-121111!31111n n n + )!1(1+n ;11111⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-n n n注意到 ,11111⎪⎭⎫ ⎝⎛+-<⎪⎭⎫ ⎝⎛-n n ,12121⎪⎭⎫ ⎝⎛+-<⎪⎭⎫ ⎝⎛-n n .11111 ,⎪⎭⎫⎝⎛+--<⎪⎭⎫ ⎝⎛--n n n n且1+n x 比n x 多一项)!1(1+n ,011111>⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-n n n , 1n n x x >⇒+ 即n x ↗.nn n x n )1(132121111!1!31!21110-++⋅+⋅++<+++++<< n x n n n .31111111312121111⇒<-++=⎪⎭⎫ ⎝⎛--++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-++= 有界.综上, 数列{n x }单调有界.评注 该证法朴素而稳健, 不失大将风度.证法二 ( 利用Bernoulli 不等式 )注意到Bernoulli 不等式 n x nx x n ,1( ,1)1(->+≥+为正整数 ), 有=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++=++nn nn n n x x 1111111nn n n ⎪⎪⎪⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛++11111111=⎪⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛++=n n n n n n 12211122,)1(111112nn n ⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛++= 由 ,1)1(12->+-n 利用Bernoulli 不等式,有 .1133233)1(1111232321>++++++=⎪⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛++≥+n n n n n n n n n x x n n n x ⇒↗. 为证{n x }上方有界, 考虑数列 .111+⎪⎭⎫ ⎝⎛+=n n n y 可类证n y ↘. 事实上,=+1n n y y =⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+++2111111n n n n 1111111111+⎪⎪⎪⎪⎭⎫ ⎝⎛+++++n n n n 12221221+⎪⎪⎭⎫ ⎝⎛+++++=n n n n n n n ⎪⎭⎫⎝⎛+++++≥⎪⎭⎫⎝⎛++++=+n n n n n n n n n n 2112121121212 (此处利用了Bernoulli 不等式 ) n y nn n n n n ,1441442323⇒>+++++=↘.显然有 , .n y x n n ∀⇒< 有 .41=≤≤<y y x n n 即数列{n y }有上界. 评注 该证法的特点是惊而无险，恰到好处.证法三( 利用均值不等式 ) 在均值不等式 )0( ,1121>≤∑=i ni i nn a a n a a a中, 令 ,1 ,111121=-+====-n n a n a a a 就有 ,11111111)1(1 111111n n n nn n nn x n n n n n n x =⎪⎭⎫ ⎝⎛+=+=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-+-≤⋅⎪⎭⎫ ⎝⎛--=-- , 1n n x x ≤⇒- 即 n x ↗.令 ,1 ,111121=--====-n n a n a a a 可仿上证得 3≥n 时⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛-nn 11↗,( 1=n 时无意义, 2=n 时诸i a =0, 不能用均值不等式. ) 当2≥n 时, 由2111111111, 1,11n n n n n⎛⎫⎛⎫+-=-<⇒+< ⎪⎪⎝⎭⎝⎭- .11111 n nn n ⎪⎭⎫ ⎝⎛-<⎪⎭⎫ ⎝⎛+∴ 由 nn ⎪⎭⎫⎝⎛-11↗n n ⎪⎭⎫ ⎝⎛-⇒111 ↘. 22111 ⎪⎭⎫⎝⎛-<⇒n x < 4. 评注 该证法很奇巧. 以上证法二和证法三可参阅《数学通报》1980.№4 P22.证法四 ( 仍利用均值不等式 )个n nn n n n ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+111111111⋅ , .111121111 1111++++<⇒⎪⎭⎫ ⎝⎛++=⎪⎭⎫⎝⎛++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++⎪⎭⎫ ⎝⎛+<n n n n n x x n n n n n n 即 n x ↗.有界性证法可参阅上述各证法.评注 该证法以简单而奇妙见长. 证法四可参阅《数学教案研究》1991.№1 马德尧 文“均值不等式妙用两则”.证法五 先证明：对 b a <≤∀0和正整数n ，有不等式.)1(11n n n b n ab a b +<--++事实上，=-++++-=----++ab a ba a b b a b a b a b nn n n n n 1111)(( n n n n a ba a b b ++++--11 < .)1(n b n +该不等式又可变形为[],)1(1+<-+n n a nb a n b ( n b a ,0<≤为正整数 )在此不等式中, 取 ,11 ,111nb n a +=++= 则有 ,0b a <≤ 就有 n n nx n n ,111111⇒⎪⎭⎫ ⎝⎛++<⎪⎭⎫ ⎝⎛++↗.取 ,211 ,1n b a +== 又有 121211<⋅⎪⎭⎫ ⎝⎛+n n 对n ∀成立，⇒<⎪⎭⎫ ⎝⎛+⇒ ,2211 nn.421122<⎪⎭⎫ ⎝⎛+=nnn x 又由 .4 ,212<⇒<-n n n x x x评注 该证法真叫绝.教材采用这一证法. 可参阅《The American Mathematical Monthly 》 1974. Vol 81. №9 P10—11。

§2.3 数列极限存在的条件教案内容：第二章 数列极限 ——§2.3 数列极限存在的条件 教案目标：使学生掌握判断数列极限存在的常用工具.教案要求：(1) 掌握并会证明单调有界定理，并会运用它求某些收敛数列的极限；(2) 初步理解Cauchy 准则在极限理论中的主要意义，并逐步会应用Cauchy 准则判断某些数列的敛散性.教案重点：单调有界定理、Cauchy 收敛准则及其应用. 教案难点：相关定理的应用. 教案方法：讲练结合. 教案过程： 引言在研究比较复杂的极限问题时，通常分两步来解决：先判断该数列是否有极限（极限的存在性问题）；若有极限，再考虑如何计算些极限（极限值的计算问题）.这是极限理论的两基本问题.在实际应用中，解决了数列{}n a 极限的存在性问题之后，即使极限值的计算较为困难，但由于当n 充分大时，n a 能充分接近其极限a ，故可用n a 作为a 的近似值.本节将重点讨论极限的存在性问题.为了确定某个数列是否有极限，当然不可能将每一个实数依定义一一加以验证，根本的办法是直接从数列本身的特征来作出判断.从收敛数列的有界性可知：若{}n a 收敛，则{}n a 为有界数列；但反之不一定对，即{}n a 有界不足以保证{}n a 收敛.例如{}(1)n -.但直观看来，若{}n a 有界，又{}n a 随n 的增大（减少）而增大（减少），它就有可能与其上界（或下界）非常接近，从而有可能存在极限（或收敛）.为了说明这一点，先给出具有上述特征的数列一个名称——单调数列. 一、单调数列定义 若数列{}n a 的各项满足不等式11()n n n a a a a ++≤≥，则称{}n a 为递增（递减）数列.递增和递减数列统称为单调数列．例如：1n ⎧⎫⎨⎬⎩⎭为递减数列；{}2n 为递增数列；(1)n n ⎧⎫-⎨⎬⎩⎭不是单调数列.二、单调有界定理问题 （1）单调数列一定收敛吗？；（2）收敛数列一定单调吗？一个数列{}n a ，如果仅是单调的或有界的，不足以保证其收敛，但若既单调又有界，就可以了.此即下面的极限存在的判断方法.定理（单调有界定理） 在实数系中，有界且单调数列必有极限. 几何解释 单调数列}{n a 只可能向一个方向移动，故仅有两种可能：（1）点na 沿数轴移向无穷远；（2）na 无限趋于某一个定点A ，即)(∞→→n A a n .证明 不妨设}{n a 单调增加有上界，把}{n a 看作集合，有确界原理，μ=}sup{n a 存在即：（1）n ∀，μ≤n a ；（2）0>∀ε，N n ∈∃0使0n a εμ->,由于}{n a 单调增加，故当0n n >时有εμ-<0n a εμμ+<≤≤n a即当n n >时εμ<-||n a 亦即μ=∞→n n a lim .例10>a ，证明数列a a =1，a a a +=2，a a a a ++=3，……，n a a=++，……收敛，并求其极限.证明 从该数列的构造，显见它是单调增加的，下面来证它是有界的.易见0>≥a a n ，且12a a a +=，23a a a +=，…，1-+=n n a a a ，…,从而12-+=n n a a a na a +< 两端除以na 得nn a aa +<1,n ∀，a a n ≥ ⇒ a a a n +<≤1 故}{n a 有界即得极限存在.设∞→n lim l a n=，对等式12-+=n n a a a 两边取极限，则有)(lim lim 12-∞→∞→+=n n n n a a a =aa n n +-∞→1lim ⇒al l +=22411al +±=⇒,因}{n a 为正数列，故0≥l ，因此取2411al ++=即为所求极限.例2 求∞→n lim nka n （k 为一定数，1>a ）解 记=n c n ka n ，则0>n c 且kk n n n a n n a c c )11(1)1(11+=+=+1>a ，则N ∃，当N n >时1)11(1<+k n a ，故N n >后，}{n c 单调递减，又有0>n c ⇒极限一定存在，设为A ,由n k n c n a c )11(11+=+两边取极限得A a A 1=（1>a ）0=⇒A . 例3 设 ). 2 ( ,131211≥++++=ααααna n 证明数列{n a }收敛. 例4.21 .0 ,011⎪⎪⎭⎫⎝⎛+=>>+n n n x a x x x a 求.lim n n x ∞→ ( 计算a 的逐次逼近法, 亦即迭代法 ). 解 由均值不等式, 有⎪⎪⎭⎫ ⎝⎛+=+n n n x a x x 21 1}{ .n nn x a x ax ⇒=⋅≥有下界,注意到对,n ∀有,a x n ≥有nn n n x a a x a x x .1) (121121221⇒=⎪⎪⎭⎫ ⎝⎛+≤⎪⎪⎭⎫ ⎝⎛+=+↘，,.lim a x n n =∞→三、柯西收敛准则 (一) 引言单调有界定理只是数列收敛的充分条件，下面给出在实数集中数列收敛的充分必要条件——柯西收敛准则. (二) Cauchy 收敛准则定理（Ｃauchy 收敛准则） 数列{}n a 收敛的充分必要条件是：对任给的0ε>，存在正整数Ｎ，使得当,n m N >时有||n m a a ε-<.证明“⇒”}{n a 收敛，则存在极限，设a a n n =∞→lim ，则0>∀ε，N ∃，当N n >时有2/||ε<-a a n ⇒当N m n >,时有ε<-+-≤-||||||a a a a a a n m m n“⇐”先证有界性，取1=ε，则N ∃，N m n >,⇒1||<-m n a a .特别地，N n >时1||1<-+N n a a ⇒1||||1+<+N n a a ,设}1|||,|,|,||,m ax {|121+=+N N a a a a M ，则n ∀，Ma n ≤||.再由致密性定理知，}{n a 有收敛子列}{k n a ，设aa k n k =∞→lim ,0>∀ε，1N ∃，1,N m n >⇒||/2n m a a ε-<,K ∃，K k >⇒2/||ε<-a a k n ,取),m ax (1N K N =，当N n >时有11N n N N +≥+>⇒ εεε=+<-+-≤-++2/2/||||||11a a a a a a N N n n n n ,故a a n k =∞→limCauchy 列、基本列（满足Cauchy 收敛准则的数列） Cauchy 收敛准则的另一表示形式：0>∀ε，N ∃，当N n >时，对P +∀∈=Z 有ε<-+||n P n a a .(三) 说明1、auchy 收敛准则从理论上完全解决了数列极限的存在性问题.2、auchy 收敛准则的条件称为Ｃauchy 条件，它反映这样的事实：收敛数列各项的值愈到后面，彼此愈接近，以至于充分后面的任何两项之差的绝对值可以小于预先给定的任意小正数.或者，形象地说，收敛数列的各项越到后面越是“挤”在一起.3、auchy 准则把N ε-定义中n a 与a 的之差换成n a 与m a 之差.其好处在于无需借助数列以外的数a ，只要根据数列本身的特征就可以鉴别其（收）敛（发）散性.例 如数列}{n a 满足||||11-+-≤-n n n n a a q a a （ ,3,2=n ）且10<<q ，证明数列}{n a 收敛.证明 令0||12>=-c x x ，||||11-+-≤-n n n n a a q a a 211221||||n n n q a a q x x ---≤-≤≤-||||||||1211n n p n p n p n p n n p n a a a a a a a a -++-+-≤-⇒+-+-+-+++)(132--+-++++≤n p n p n q q q c )1(11--+++=p n q q cqq q cn -≤-11. 0>∀ε，（不妨设q c-<<10ε），取]ln )1ln(1[q c qN ε-+=，则当N n >时，对任给自然数p 有ε<-<--+q cq a a n n pn 1||1.故由Cauchy 收敛准则知数列}{n x 收敛.例 证明数列n a n 1211+++= 发散.证明 要证：0>∃ε，对N ∀，必有Nm >0，0n N>使得||00ε≥-n m a a设n m >则)(1211112111||n m n n n m n n a a n m -++++++=+++++=-m nm n m m m m -=-=+++>1111 ，因此，如n m 2=，则||11/21/2m n a a -≥-=.这样，对2/10=ε，不管N 多大，如取10+=N n ，002n m =则N m >0，0n N>且212111||0000=-=-≥-m n a a n m ，这说明}{n a 不是一个Cauchy 数列.（四） 应用例5 证明: 任一无限十进小数 )10( .021<<=αα n b b b 的不足近似值所组成的数列,101010 , ,1010 ,102212211 n n b bb b b b ++++ 收敛. 其中) 9,,2,1 ( =i b i 是9,,1,0 中的数.证明 令 =n a ,101010 221n n b bb +++ 有⎪⎭⎫⎝⎛+++≤+++=--++++++++1122111011011109101010 p n p n p n n n n n n pn b b b a a1109+=n ().1101)1.0(11011.01)1.0(1n n p n p<<-=--…… 例6 设 .sin sin sin ,102n n n q q q q q q x q +++=<< 试证明数列{}n x 收敛.关于极限1lim 1nn e n →∞⎛⎫+= ⎪⎝⎭) 71828.2 (≈e 的 证明留在下节进行.例7 .11lim ,11lim knn kn n n n ⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛+∞→+∞→例8 .211lim ,11lim ,1lim 3nn nn kn n n n n c ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛+∞→∞→+∞→例9.1232lim n n n n ⎪⎭⎫⎝⎛+-∞→作业 教材P38—39 1，3，5，6，10，11；教材P40—41 1（1）（3），3，4(1)-(3)(6)(8)，5，10.（P38 3（4）提示：考虑,1nn a b =用双逼原理可求得,1→n b ）附 数列⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛+nn 11单调有界证法欣赏:Cauchy (1789—1857 ) 最先给出这一极限，Riemann （1826—1866）最先给出以下证法一.证法一 （ Riemann 最先给出这一证法 ） 设 .11nn n x ⎪⎭⎫⎝⎛+=应用二项式展开，得+⋅+=n n x n 11++⋅--+⋅- 321!3)2)(1(1!2)1(n n n n n n n n nn n n 1!123)1(⋅⋅⋅- ⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-++=n n n n n n n n 112111!12111!3111!2111 ， !21111++=+n x +⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-121111!31111n n n + )!1(1+n ;11111⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-n n n注意到 ,11111⎪⎭⎫ ⎝⎛+-<⎪⎭⎫ ⎝⎛-n n ,12121⎪⎭⎫ ⎝⎛+-<⎪⎭⎫ ⎝⎛-n n .11111 ,⎪⎭⎫⎝⎛+--<⎪⎭⎫ ⎝⎛--n n n n且1+n x 比n x 多一项)!1(1+n ,011111>⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-n n n , 1n n x x >⇒+ 即n x ↗.nn n x n )1(132121111!1!31!21110-++⋅+⋅++<+++++<< n x n n n .31111111312121111⇒<-++=⎪⎭⎫ ⎝⎛--++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-++= 有界.综上, 数列{n x }单调有界.评注 该证法朴素而稳健, 不失大将风度.证法二 ( 利用Bernoulli 不等式 )注意到Bernoulli 不等式 n x nx x n ,1( ,1)1(->+≥+为正整数 ), 有=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++=++nn nn n n x x 1111111nn n n ⎪⎪⎪⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛++11111111=⎪⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛++=n n n n n n 12211122,)1(111112nn n ⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛++= 由 ,1)1(12->+-n 利用Bernoulli 不等式,有 .1133233)1(1111232321>++++++=⎪⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛++≥+n n n n n n n n n x x n n n x ⇒↗. 为证{n x }上方有界, 考虑数列 .111+⎪⎭⎫ ⎝⎛+=n n n y 可类证n y ↘. 事实上,=+1n n y y =⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+++2111111n n n n 1111111111+⎪⎪⎪⎪⎭⎫ ⎝⎛+++++n n n n 12221221+⎪⎪⎭⎫ ⎝⎛+++++=n n n n n n n ⎪⎭⎫⎝⎛+++++≥⎪⎭⎫⎝⎛++++=+n n n n n n n n n n 2112121121212 (此处利用了Bernoulli 不等式 ) n y nn n n n n ,1441442323⇒>+++++=↘.显然有 , .n y x n n ∀⇒< 有 .41=≤≤<y y x n n 即数列{n y }有上界. 评注 该证法的特点是惊而无险，恰到好处.证法三( 利用均值不等式 ) 在均值不等式 )0( ,1121>≤∑=i ni i nn a a n a a a中, 令 ,1 ,111121=-+====-n n a n a a a 就有 ,11111111)1(1 111111n n n nn n nn x n n n n n n x =⎪⎭⎫ ⎝⎛+=+=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-+-≤⋅⎪⎭⎫ ⎝⎛--=-- , 1n n x x ≤⇒- 即 n x ↗.令 ,1 ,111121=--====-n n a n a a a 可仿上证得 3≥n 时⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛-nn 11↗,( 1=n 时无意义, 2=n 时诸i a =0, 不能用均值不等式. ) 当2≥n 时, 由2111111111, 1,11n n n n n⎛⎫⎛⎫+-=-<⇒+< ⎪⎪⎝⎭⎝⎭- .11111 n nn n ⎪⎭⎫ ⎝⎛-<⎪⎭⎫ ⎝⎛+∴ 由 nn ⎪⎭⎫⎝⎛-11↗n n ⎪⎭⎫ ⎝⎛-⇒111 ↘. 22111 ⎪⎭⎫⎝⎛-<⇒n x < 4. 评注 该证法很奇巧. 以上证法二和证法三可参阅《数学通报》1980.№4 P22.证法四 ( 仍利用均值不等式 )个n nn n n n ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+111111111⋅ , .111121111 1111++++<⇒⎪⎭⎫ ⎝⎛++=⎪⎭⎫⎝⎛++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++⎪⎭⎫ ⎝⎛+<n n n n n x x n n n n n n 即 n x ↗.有界性证法可参阅上述各证法.评注 该证法以简单而奇妙见长. 证法四可参阅《数学教案研究》1991.№1 马德尧 文“均值不等式妙用两则”.证法五 先证明：对 b a <≤∀0和正整数n ，有不等式.)1(11n n n b n ab a b +<--++事实上，=-++++-=----++ab a ba a b b a b a b a b nn n n n n 1111)(( n n n n a ba a b b ++++--11 < .)1(n b n +该不等式又可变形为[],)1(1+<-+n n a nb a n b ( n b a ,0<≤为正整数 )在此不等式中, 取 ,11 ,111nb n a +=++= 则有 ,0b a <≤ 就有 n n nx n n ,111111⇒⎪⎭⎫ ⎝⎛++<⎪⎭⎫ ⎝⎛++↗.取 ,211 ,1n b a +== 又有 121211<⋅⎪⎭⎫ ⎝⎛+n n 对n ∀成立，⇒<⎪⎭⎫ ⎝⎛+⇒ ,2211 nn.421122<⎪⎭⎫ ⎝⎛+=nnn x 又由 .4 ,212<⇒<-n n n x x x评注 该证法真叫绝.教材采用这一证法. 可参阅《The American Mathematical Monthly 》 1974. Vol 81. №9 P10—11。

数列极限存在的判定准则数列极限存在是数学中一个重要的概念，它揭示了数列在无穷项时的趋势和稳定性。

在数学分析中，数列极限存在的判定准则有以下几种：1. Cauchy准则Cauchy准则是数列极限存在的一个重要准则。

根据Cauchy准则，对于任意给定的正数ε，存在正整数N，当n>N时，对于任意正整数k，满足|an - ak| < ε。

这个准则意味着当数列中的项足够靠后时，这些项之间的差异足够小。

当且仅当数列满足Cauchy准则时，数列的极限才存在。

2. 单调有界准则对于递增（或递减）且有上（或下）界的数列，它的极限存在。

更加具体地，如果数列满足以下条件之一： - 若存在正整数N，当n>N时，有an≤an+1； - 若存在正整数N，当n>N时，有an≥an+1； - 数列有上（或下）界。

以上条件满足之一时，数列的极限存在。

3. 夹逼准则夹逼准则也是数列极限存在的判定准则之一。

如果存在两个数列{an}和{cn}，且满足an≤bn≤cn，并且当n趋近于无穷大时，an和cn都趋近于同一个极限L，那么数列{bn}的极限也收敛于L。

4. 有界性与单调性的整体准则一个数列，如果它是有界的，并且通过去除它的有限项后，剩余的数列具有单调性，那么原始数列的极限存在。

更准确地说，如果数列满足以下条件： - 存在正实数M，使得当n为任意正整数时，有|an|≤M； - 存在正整数N，当n>N时，an+1≥an或an+1≤an；则数列的极限存在。

5. 收敛数列算术运算性质如果两个数列{an}和{bn}收敛于a和b，那么它们的和、差、乘积和商也会收敛，并且有以下性质： - 和的极限为a + b； - 差的极限为a - b； - 乘积的极限为a * b； - 商的极限为a / b（其中b不等于0）。

这个准则告诉我们，如果知道一个数列收敛，并且知道另一个数列与之相关（通过加减乘除操作），我们可以利用这些关系判断极限的存在与值。