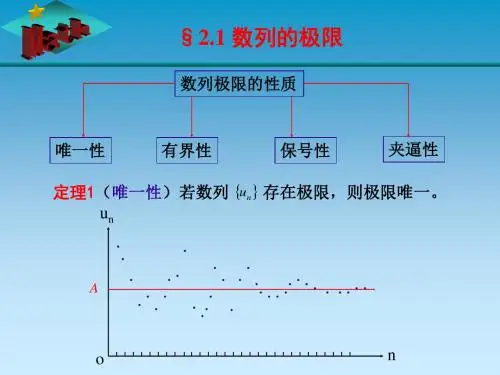
数列的极限的性质

数列的极限知识点归纳总结数列的极限是高中数学中重要的概念之一，它在解析几何、微积分等数学领域中起着重要的作用。

本文将对数列的极限进行知识点归纳总结，帮助读者更好地理解和掌握这一概念。

一、定义和概念1. 数列的定义：数列是按照一定顺序排列的一组数的集合。

数列可以用公式表示，常用的表示方式为{an}或{an}∞n=1。

2. 数列的极限定义：对于数列{an}，如果存在一个实数a，对于任意给定的正数ε，都存在正整数N，使得当n>N时，有|an - a| < ε，那么称数列{an}的极限为a。

3. 数列的收敛和发散：如果数列{an}存在极限，称该数列收敛；否则，称该数列发散。

二、极限的性质1. 极限唯一性：如果数列{an}收敛，那么它的极限是唯一的。

2. 有界性：对于收敛数列{an}，存在一个正数M，使得对于任意的n，有|an| ≤ M。

3. 夹逼定理：如果{an} ≤ {bn} ≤ {cn}，并且lim an = lim cn = a，那么lim bn = a。

4. 四则运算法则：若数列{an}和{bn}收敛，并且lim an = a，lim bn = b，则有以下运算结果：- lim(an ± bn) = a ± b- lim(an · bn) = a · b- lim(an / bn) = a / b (b ≠ 0)三、重要的数列极限1. 常数数列：对于常数c，数列{an} = c（n为正整数）的极限为c。

2. 等差数列：对于等差数列{an} = a1 + (n - 1)d，其中a1为首项，d为公差，极限为lim an = a1。

3. 等比数列：对于等比数列{an} = a1 · q^(n - 1)，其中a1为首项，q为公比，当|q| < 1时，极限为lim an = 0；当|q| > 1时，极限不存在。

4. 幂函数数列：对于幂函数数列{an} = n^p，其中p为实数，当p >0时，极限为正无穷大；当p < 0时，极限为0。

大学数列的极限知识点归纳总结数列是数学中常见且重要的概念之一，它含有很多有趣而具有挑战性的性质。

其中，数列的极限是数学分析中的重要内容之一，它在微积分、实变函数等领域中有广泛的应用。

本文将对大学数列的极限知识点进行归纳总结，帮助读者更好地理解和掌握这一概念。

一、数列的定义及性质1. 数列的定义：数列是按照一定顺序排列的一串数字。

2. 数列的记法：一般用 {an} 表示数列，其中 an 表示数列的第n项。

3. 数列的性质：数列可以是有界的或无界的。

二、数列极限的概念1. 数列极限的定义：对于数列 {an}，如果存在一个常数A，使得对于任意给定的正数ε，存在正整数N，使得当n>N时，|an-A|<ε，那么称数列的极限为A，记作lim (n→∞) an = A。

2. 数列极限的几何解释：数列的极限可以理解为当n趋向于无穷大时，数列的项趋向于某个常数。

三、数列极限的性质1. 数列极限的唯一性：对于一个数列，如果其极限存在，则该极限是唯一的。

2. 数列极限与数列项的关系：如果数列的极限存在，那么对于任意大于极限的数M，存在正整数N，使得当n>N时，an>M。

3. 数列极限与数列的有界性的关系：如果数列的极限存在，那么这个数列一定是有界的。

四、常见数列的极限1. 等差数列的极限：对于等差数列 {an} = a1, a1+d, a1+2d, ...，其中a1为首项，d为公差，其极限为lim (n→∞) an = a1。

2. 等比数列的极限：对于等比数列 {an} = a1, a1r, a1r^2, ...，其中a1为首项，r为公比（r≠0），其极限存在的条件是|r|<1，极限为lim(n→∞) an = 0。

3. 斐波那契数列的极限：斐波那契数列 {Fn} = 1, 1, 2, 3, 5, 8, ...，其中每一项等于前两项之和。

斐波那契数列的极限不存在，即lim (n→∞) Fn 不存在。

数列极限知识点归纳总结数列是数学中的一个重要概念，由一系列有序的数字组成。

数列极限是数列在无穷项处的趋势或趋近的值。

在数学分析中，数列极限是一个基本的概念，具有广泛的应用。

本文将对数列极限的相关知识进行归纳总结，并以此为标题。

一、数列的定义和性质1. 数列的定义：数列是按照一定的规律排列的一系列数字。

2. 数列的通项公式：数列中的每一项可以用一个公式来表示，这个公式称为数列的通项公式。

3. 数列的性质：数列可以是有界的或无界的，可以是递增的或递减的，还可以是周期性的或非周期性的。

二、数列的极限1. 数列的极限定义：对于一个数列，如果随着项数的增加，数列中的元素逐渐接近一个确定的值，那么这个确定的值就是数列的极限。

2. 数列极限的表示：数列极限常用符号lim表示，写作lim(an)=a，其中an为数列的第n项，a为数列的极限。

3. 数列极限的存在性：数列的极限可能存在，也可能不存在。

如果数列极限存在，则称数列收敛；如果数列极限不存在，则称数列发散。

三、数列极限的计算方法1. 直接计算法：对于一些简单的数列，可以通过对数列的通项公式进行计算，得到数列的极限。

2. 套路法：对于一些特殊的数列，可以利用一些已知的极限结果和数列运算的性质，通过一些套路求得数列的极限。

3. 夹逼准则：对于一些复杂的数列，可以通过夹逼准则来求得数列的极限。

夹逼准则指的是如果数列a(n)≤b(n)≤c(n)，且lim(a(n))=lim(c(n))=a，那么lim(b(n))=a。

四、数列极限的性质1. 唯一性：如果数列极限存在，则极限值唯一。

2. 保号性：如果数列的极限为正数（负数），那么数列的项数足够大时，数列的元素大于（小于）零。

3. 有界性：如果数列的极限存在，则数列有界。

五、数列极限的应用1. 函数极限：函数极限是数列极限的推广，通过将自变量取为数列，将函数值作为数列的项，就可以研究函数的极限。

2. 数列极限在微积分中的应用：数列极限在微积分中有广泛的应用，如计算导数、积分等。

数列的极限与通项公式数列是数学中的一个重要概念，经常在各个领域中被使用。

数列的极限与通项公式是数列研究中的关键内容，本文将介绍数列的基本概念，探讨数列极限及其性质，最后讲解数列的通项公式及应用。

一、数列的基本概念数列是由一系列按照特定规律排列的数字组成的序列。

一般用字母表示数列的一般项，常用形式为{a_n}或(a_1, a_2, a_3, ...)。

其中，a_n表示数列的第n项，n表示项的顺序。

二、数列的极限数列的极限是指当数列中的项数趋于无穷大时，数列中的项的极限值。

记作lim(a_n)或a_n→∞。

1. 数列的极限存在若存在一个实数L，使得对于任意给定的正数ε，都存在正整数N，当n>N时，有|a_n - L| < ε，则称L为数列{a_n}的极限，并记作lim(a_n) = L。

2. 数列的极限性质（1）极限的唯一性：如果数列{a_n}有极限，则极限是唯一的。

（2）夹逼准则：若数列{a_n}，{b_n}，{c_n}满足a_n ≤ b_n ≤ c_n，并且lim(a_n) = lim(c_n) = L，则lim(b_n) = L。

（3）有界性：若数列{a_n}有极限，则数列是有界的。

（4）收敛数列与发散数列：若数列{a_n}有极限，则称之为收敛数列；反之，称为发散数列。

三、数列的通项公式数列的通项公式是表示数列第n项的一般形式。

通过通项公式，我们可以根据项的顺序n计算数列中的特定项的值。

1. 等差数列的通项公式等差数列是指数列中任意两个相邻项之差都相等的数列。

若等差数列的首项为a_1，公差为d，则它的通项公式为a_n = a_1 + (n-1)d。

2. 等比数列的通项公式等比数列是指数列中任意两个相邻项之比都相等的数列。

若等比数列的首项为a_1，公比为q，则它的通项公式为a_n = a_1 * q^(n-1)。

3. 斐波那契数列的通项公式斐波那契数列是指首项和第二项都为1，从第三项开始，每一项都是前两项之和的数列。

数列的极限
一，数列极限定义
简单来讲就是：一个数列随着序数的增加最终会趋于或等于一个数，这个数就是数列的极限。

证明题要结合书上的公式
二，收敛数列的性质
1唯一性：收敛数列只有一个极限
2有界性：收敛数列一定有界。

(收敛数列最终都会趋于或等于一个数，所以有界)但有界数列不一定就是收敛数列，如-1，1，-1，1……,这个数列就是发散的，因为它同时趋于-1和1。

（有界是因为它的绝对值小于等于1，可参考上节所讲如何判定数列有界）这个数列同时说明了发散数列不一定无界。

3保号性：就是有一个数列，当其中一个数从它开始大于零，那么它之后的数都大于零。

推论：当一个数列存在某一个数大于零，那么这个数列的极限也大于零
4收敛数列与其子数列间的关系：如果一个数列收敛于A，那么它的任意子数列也收敛于A，但子数列收敛，原数列不一定收敛；子数列收敛于A，原数列不一定收敛于A，有可能原数列不收敛，可参考我在有界性中提到的例子，同时这个例子也说明一个发散的数列也可能有收敛的子数列。

数列极限的知识点总结一、数列极限的定义1.1 数列首先要了解数列的概念。

数列是由一系列按照一定顺序排列的数所组成的有序集合。

数列通常用符号{an}表示，其中an代表数列的第n个元素。

数列是数学中一种基本的数学概念，它在许多数学问题中都起着重要的作用。

1.2 数列极限接着要了解数列的极限。

数列{an}的极限是指当n趋向于无穷大时，数列中的元素an的值趋近于一个常数L，即lim(an) = L。

如果这样一个数L存在，那么我们就说数列{an}收敛，并且把L称为数列的极限，记作lim(an) = L。

如果这样一个数L不存在，那么我们就说数列{an}发散。

1.3 数列极限的形式化定义对于给定的数ε，如果存在一个正整数N，使得当n大于N时，|an - L| < ε恒成立，那么称L是数列{an}的极限。

这样的N存在的话，就称这N是数L和ε的函数。

1.4 无穷大数列如果数列{an}中的元素an当n趋向于无穷大时，它的绝对值|an|趋向于无穷大，那么就称数列{an}是无穷大的。

对于无穷大数列，我们通常用符号lim(an) = ±∞来表示。

1.5 注意事项在讨论数列极限的问题时，需要注意以下几点：1) 数列的极限可能是一个有限的常数，也可能是无穷大。

2) 一般来说，数列的极限不一定存在，也可能有多个极限（一般在不同n的取值范围内）。

3) 要特别注意当n趋于无穷大时，数列中的元素an的绝对值的行为，关系到数列是否是无穷大数列。

以上是数列极限的基本概念和定义，下面我们将介绍数列极限的相关性质。

二、数列极限的相关性质2.1 唯一性如果数列{an}收敛，那么它的极限是唯一的。

换句话说，如果lim(an) = L1和lim(an) = L2，那么L1 = L2。

2.2 有界性如果数列{an}收敛，那么它一定是有界的，即存在一个正实数M，使得|an| < M（n∈N）。

2.3 保号性如果数列{an}收敛到一个有限的极限L，那么当n充分大时，数列{an}的元素和L有相同的正负号。

数列的极限概念与收敛性判定数列作为数学中的一种重要概念，在许多领域中有着广泛的应用。

数列的极限概念与收敛性判定是数列研究中的重要内容。

本文将围绕这一主题展开讨论，分析数列的极限概念以及如何判定数列的收敛性，旨在深入理解数列的相关知识。

一、数列的极限概念数列的极限是指随着自变量趋于无穷大（或无穷小），函数值趋于某个常数。

对于数列{an}来说，如果存在常数a，对于任意给定的正数ε，都存在正整数N，使得当n大于N时，对应的数列值an与常数a的差的绝对值小于ε，即|an-a|<ε，则称常数a为数列{an}的极限，记作lim(an)=a。

在数列的极限概念中，数列的极限可以是有限的也可以是无限的。

如果数列的极限存在且为有限数，即满足lim(an)=a，则称数列{an}收敛于a。

如果数列的极限不存在或为无穷大或无穷小，即lim(an)不存在或为正无穷、负无穷或无穷小，则称数列{an}为发散数列。

二、数列收敛性判定的方法1. 有界性判定：如果数列{an}存在上界和下界，即存在常数M和m，使得对于任意的n，有m≤an≤M成立，则称数列{an}是有界的。

定理称为有界收敛定理：一个数列收敛的充分必要条件是它有界。

2. 单调性判定：如果数列{an}为单调递增数列且有上界，或为单调递减数列且有下界，则数列{an}收敛。

单调数列的收敛性可由单调有界原理来推导。

3. 函数逼近法：将数列的极限与函数的极限相联系，利用函数的性质进行判定。

例如，若数列{an}收敛于a，则函数f(x)在点a处连续。

4. 递推关系式判定：对于递推数列的情况，通过确定递推关系式，可以利用已知的数学方法判断数列的收敛性。

例如，斐波那契数列的极限存在且为无穷。

除了上述方法，还有一些特殊的数列判定方法，如柯西收敛准则、夹逼定理等，可以根据具体问题的特点选择合适的方法进行判定。

三、数列极限的性质1. 数列极限的唯一性：数列的极限如果存在，则极限值唯一。

即如果lim(an)=a且lim(an)=b，那么a=b。

高三数学《数列的极限》基础知识与解题技巧教案引言：数列的极限是高中数学中重要的概念之一，是初步接触数学分析的起点。

本教案将从数列的定义开始，介绍数列的极限的基础知识和解题技巧，帮助学生全面理解和掌握这一概念。

一、数列的定义及基本概念1. 数列的定义：数列是按照一定顺序排列的一组实数。

2. 数列的通项公式：数列中的每一项可以用一个公式来表示，这个公式就是数列的通项公式。

3. 数列的前n项和：数列的前n项和指的是数列的前n个数相加的结果，通常用Sn表示。

二、数列的极限的定义与性质1. 数列的极限定义：当数列中的每一项趋近于一个常数L时，称L 为数列的极限，记作lim(a_n) = L。

2. 数列极限的性质：a) 唯一性：数列的极限如果存在，那么极限是唯一的。

b) 保号性：如果数列中的每一项都大于等于（或小于等于）一个常数A，并且极限L存在，那么L也大于等于（或小于等于）A。

c) 夹逼性：如果数列中的每一项都大于等于（或小于等于）一个数列b_n，并且极限L存在，那么b_n也大于等于（或小于等于）L。

三、数列极限的计算方法1. 利用通项公式计算极限：当数列的通项公式为简单的初等函数表达式时，可以使用代入法或化简法计算极限。

2. 利用数列的性质计算极限：a) 有界性：如果数列有界，并且存在所谓的上（下）确界，那么极限即为上（下）确界。

b) 递推关系：当数列的递推关系表示式演化到极限形式时，可以通过解递推方程求解极限。

四、常见数列的极限及其性质1. 等差数列的极限：当等差数列的公差为零时，数列为常数数列，极限即为常数本身；当公差不为零时，极限不存在。

2. 等比数列的极限：当等比数列的公比绝对值小于1时，数列趋于0；当公比绝对值大于1时，极限不存在。

3. 斐波那契数列的极限：斐波那契数列的极限是黄金比例φ = (1 + √5) / 2。

五、数列极限的解题步骤1. 理解题目要求，确定数列的通项公式。

2. 判断数列的性质和是否有已知极限，选择合适的计算方法。