下载文档原格式
平面内点的坐标知识点总结 1、平面直角坐标系定义：平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系，简称为直角坐标系。
水平的数轴叫做X 轴或横轴，取向右为正方向；垂直的数轴叫做Y 轴或纵轴，取向 上为正方向；两轴交点O 为原点。
点的坐标：对于坐标平面内的任意一点P ，过点p 向x 轴作垂线，垂足在x 轴上的坐标为p x ，则p x 叫做点p 的横坐标，过点p 向y 轴作垂线，垂轴在y 上的坐标为py ，则py 叫做点p 纵坐标。
点p 的坐标记为点(),p p p x y 。
注意（1）坐标平面内的点和有序实数对是一一对应的；（2）表示点的坐标的两个数是有顺序的，当a b ≠时，点(),p a b 与(),Q a b 表示两个不同的点。
2、坐标平面内点的坐标特点 （1）各个象限内点的特征:第一象限：（+，+） 点P （x,y ），则x ＞0,y ＞0； 第二象限：（-，+） 点P （x,y ），则x ＜0,y ＞0； 第三象限：（-，-） 点P （x,y ），则x ＜0,y ＜0； 第四象限：（+，-） 点P （x,y ），则x ＞0,y ＜0； 在x 轴上：（x,0） 点P （x,y ），则y ＝0；在x 轴的正半轴：（+，0） 点P （x,y ），则x ＞0,y ＝0；在x轴的负半轴：（-，0）点P（x,y），则x＜0,y＝0；在y轴上：（0,y）点P（x,y），则x＝0；在y轴的正半轴：（0，+）点P（x,y），则x＝0,y＞0；在y轴的负半轴：（0，-）点P（x,y），则x＝0,y＜0；坐标原点：（0，0）点P（x,y），则x＝0,y＝0；（2）与x轴，y轴平行的直线上的点的坐标特点点(),a b不与原点重合，过(),a b点与x轴平行的直线上的点的纵坐标都是b，这条直线可表示为y b=；过(),a b点与y轴平行的直线上的点的横坐标都是a，这条直线可表示为x a=；反之也成立。
（3）点()p x y到x轴的距离为y，到y轴的距离为x。
平面内点的坐标我们在一个平面内构造两条互相垂直的数轴Ox和Oy。
它们的交点是坐标原点。
我们分别称轴Ox和Oy是x轴和y轴（轴Ox和Oy也可以叫做坐标轴或坐标的轴），同时，它们所在的平面称为Oxy平面。
我们认为两个坐标轴的长度单位是一样的。
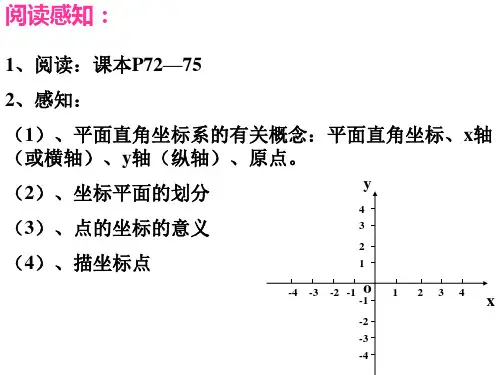
Ox轴和Oy轴把Oxy平面分为四个象限，它们相应于坐标轴方向的编号如图2所示。
我们考虑平面Oxy上一点P，P x和P y是点P向Ox轴和Oy轴引的垂足，亦即点P在这些轴上的垂直投影。
我们用x表示P x在x轴上的坐标。
用y表示P y在y轴上的坐标。
数x和y 称为点P的坐标，表示为P(x，y)。
这种类型的坐标称为笛卡儿直角坐标①所以，在一个平面中确定点P的坐标导致分别在两数轴上确定两个点(P x和P y)的坐标。
点P x的坐标x称为点P的横坐标；点P y的坐标y称为点P的纵坐标。
如果点P位于Ox 轴上，则其纵坐标为零；如果点P位于Oy轴上，则其横坐标为零。
O点的横、纵坐标皆为零。
图4所示是点在不同象限中其坐标的符号；左边是横坐标的符号，右边是纵坐标的符号。
现在我们来指出，如果知道了点P的坐标x和y，如何确定点P。
我们根据P x的横坐标x在Ox轴上标出点P x，根据P y的纵坐标y在Oy轴上标出点P y；(见图3)，然后，通过P x对Ox轴作垂线，通过P y对Oy轴作垂线。
这两条垂线的交点即为我们想要得到的点P。
上面的作图可以用下面的方法进行修改(图5)：通过点P x对Ox轴画一条垂线，然后在垂线上以坐标y的绝对值为长度截取一线段P x P，而且，如果y＞0，则从点P x向上取，如果y＜0，则从点P x向下取（更确切地说，如果y＞0，点P和Oy轴的正半轴必须位于Ox轴的同侧；如果y＜0，则位于异侧。
以后，我们不给出详尽的描述，都认为Ox轴的正半轴位于Ox轴负半轴的右侧，Oy轴的正半轴在Oy的负半轴的上方）。
如果y＝0，则点P与点P x重合。
在以上构造的基础上，我们可以这样说，一个点的坐标指出了从坐标原点到给定点的一条路径：知道了点P的横坐标x，我们可以找到这条路径的OP x部分，而点P的纵坐标y则给出了第二部分P x P。
