整理力法对称结构
- 格式:ppt
- 大小:1.11 MB
- 文档页数:17

第八章力法本章主要内容1)超静定结构的超静定次数2)力法的解题思路和力法典型方程(显然力法方程中所有的系数和自由项都是指静定基本结构的位移,可以由上一章的求位移方法求出(图乘或积分))3)力法的解题步骤以及用于求解超静定梁刚架桁架组合结构(排架)4)力法的对称性利用问题,对称结构的有关概念四点结论5)超静定结构的位移计算和最后内力图的校核6)§8-1超静定结构概述一、静力解答特征:静定结构:由平衡条件求出支反力及内力;超静定结构的静力特征是具有多余力,仅由静力平衡条件无法求出它的全部(有时部分可求)反力及内力,须借助位移条件(补充方程,解答的唯一性定理)。
二、几何组成特征:(结合例题说明)静定结构:无多余联系的几何不变体超静定结构:去掉其某一个或某几个联系(内或外),仍然可以是一个几何不变体系,如桁架。
即:超静定结构的组成特征是其具有多余联系,多余联系可以是外部的,也可能是内部的,去掉后不改变几何不变性。
多余联系(约束):并不是没有用的,在结构作用或调整结构的内力、位移时需要的,减小弯矩及位移,便于应力分布均匀。
多余求知力:多余联系中产生的力称为三、超静定结构的类型(五种)超静定梁、超静定刚刚架、超静定桁架、超静定拱、超静定组合结构四、超静定结构的解法综合考虑三个方面的条件:1、平衡条件:即结构的整体及任何一部分的受力状态都应满足平衡方程;2、几何条件:也称变形条件、位移条件、协调条件、相容条件等。
即结构的变形必须符合支承约束条件(边界条件)和各部分之间的变形连续条件。
3、物理条件:即变形或位移与内力之间的物理关系。
精确方法:力法(柔度法):以多余未知力为基本未知量位移法(刚度法):以位移为基本未知量。
力法与位移法的联合应用:力法与位移法的混合使用:混合法近似方法:力矩分配法、矩阵位移法、分层总和法、D值法、反弯点法等本章主要讲力法。
五、力法的解题思路(结合例子)把不会算的超静定结构通过会算的基本结构来计算。


对称性应用在工程问题中,有很多结构都具有对称性。
我们对这些结构进行受力分析的时候,常常将结构简化为杆系模型,而结构力学研究的就是结构的杆系模型,因此对称性在结构力学中有着广泛的应用。
现在就对称性在结构力学中的应用做一简单的总结。
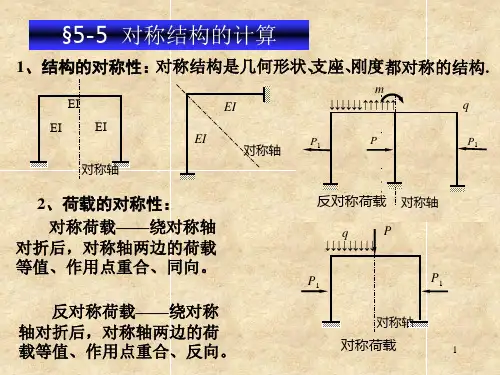
结构的对称性是指结构的几何形状和支座形式均对称于某一几何轴线。
而荷载的对称则分为正对称荷载和反对称荷载。
另外需要注意的是杆件截面和材料的性质也要对于此轴对称。
在对称荷载作用下,结构内力呈对称分布。
在反对称荷载作用下,结构内力呈反对称分布。
如下图所示:对称性在求解结构内力中的应用:对称结构在正对称荷载作用下,其对称的内力(弯矩和轴力)和位移是正对称的,其反对称的内力(剪力)是反对称的;在反对称荷载作用下,其对称的内力(弯矩和轴力)和位移是反对称的,其反对称的内力(剪力)是正对称的。
因此,只要我们做出半边结构的内力图,也就知道了整个结构的内力图。
据此,我们在对对称结构进行内力分析时,就可以取半边结构进行分析。
取半边结构进行分析,可以减少超静定次数,减少基本未知量,为解题提供了很大的方便。
在用力法解决超静定问题时,对于对称的结构,可利用对称性简化计算。
简化步骤如下:1、选取对称的基本结构。
2、将未知力及荷载分组。
3、取半结构进行计算。
对于对称结构承受一般非对称荷载时,利用荷载分组,将荷载分解为正、反对称的两组,并将他们分别作用于结构上求解内力,然后将计算结果叠加。
在计算对称结构时,根据对称结构特性,可以选取半个结构计算。
选取半结构的原则:1、在对称轴的截面或位于对称轴的节点处2、按原结构的静力和位移条件设置相应的支撑,使半结构与原结构的内力和变形完全等效偶数跨对称结构: £8-15在用位移法求解超静定结构的时候,同样可以利用对称性简化计算。
分析可 知,在正对称荷载时用位移法求解只有一个基本未知量; 但在反对称荷载时若用 位移法求解将有两个基本未知量, 而用力法求解则只有一个未知量。

对称性应用在工程问题中,有很多结构都具有对称性。
我们对这些结构进行受力分析的时候,常常将结构简化为杆系模型,而结构力学研究的就是结构的杆系模型,因此对称性在结构力学中有着广泛的应用。
现在就对称性在结构力学中的应用做一简单的总结。
结构的对称性是指结构的几何形状和支座形式均对称于某一几何轴线。
而荷载的对称则分为正对称荷载和反对称荷载。
另外需要注意的是杆件截面和材料的性质也要对于此轴对称。
在对称荷载作用下,结构内力呈对称分布。
在反对称荷载作用下,结构内力呈反对称分布。
如下图所示:对称性在求解结构内力中的应用:对称结构在正对称荷载作用下,其对称的内力(弯矩和轴力)和位移是正对称的,其反对称的内力(剪力)是反对称的;在反对称荷载作用下,其对称的内力(弯矩和轴力)和位移是反对称的,其反对称的内力(剪力)是正对称的。
因此,只要我们做出半边结构的内力图,也就知道了整个结构的内力图。
据此,我们在对对称结构进行内力分析时,就可以取半边结构进行分析。
取半边结构进行分析,可以减少超静定次数,减少基本未知量,为解题提供了很大的方便。
在用力法解决超静定问题时,对于对称的结构,可利用对称性简化计算。
简化步骤如下:1、选取对称的基本结构。
2、将未知力及荷载分组。
3、取半结构进行计算。
对于对称结构承受一般非对称荷载时,利用荷载分组,将荷载分解为正、反对称的两组,并将他们分别作用于结构上求解内力,然后将计算结果叠加。
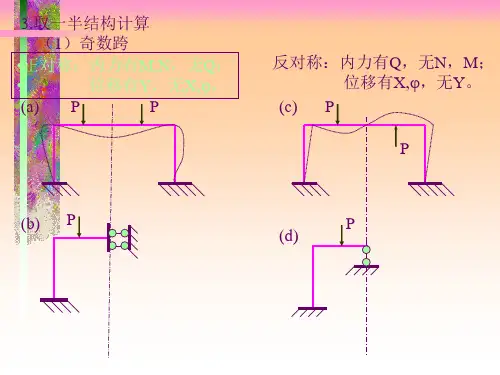
反对称正对称在计算对称结构时,根据对称结构特性,可以选取半个结构计算。
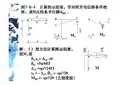
选取半结构的原则:1、在对称轴的截面或位于对称轴的节点处2、按原结构的静力和位移条件设置相应的支撑,使半结构与原结构的内力和变形完全等效奇数跨对称结构:偶数跨对称结构:在用位移法求解超静定结构的时候,同样可以利用对称性简化计算。
分析可知,在正对称荷载时用位移法求解只有一个基本未知量;但在反对称荷载时若用位移法求解将有两个基本未知量,而用力法求解则只有一个未知量。


对称性应用在工程问题中,有很多结构都具有对称性。
我们对这些结构进行受力分析的时候,常常将结构简化为杆系模型,而结构力学研究的就是结构的杆系模型,因此对称性在结构力学中有着广泛的应用。
现在就对称性在结构力学中的应用做一简单的总结。
结构的对称性是指结构的几何形状和支座形式均对称于某一几何轴线。
而荷载的对称则分为正对称荷载和反对称荷载。
另外需要注意的是杆件截面和材料的性质也要对于此轴对称。
在对称荷载作用下,结构内力呈对称分布。
在反对称荷载作用下,结构内力呈反对称分布。
如下图所示:对称性在求解结构内力中的应用:对称结构在正对称荷载作用下,其对称的内力(弯矩和轴力)和位移是正对称的,其反对称的内力(剪力)是反对称的;在反对称荷载作用下,其对称的内力(弯矩和轴力)和位移是反对称的,其反对称的内力(剪力)是正对称的。
因此,只要我们做出半边结构的内力图,也就知道了整个结构的内力图。
据此,我们在对对称结构进行内力分析时,就可以取半边结构进行分析。
取半边结构进行分析,可以减少超静定次数,减少基本未知量,为解题提供了很大的方便。
在用力法解决超静定问题时,对于对称的结构,可利用对称性简化计算。
简化步骤如下:1、选取对称的基本结构。
2、将未知力及荷载分组。
3、取半结构进行计算。
对于对称结构承受一般非对称荷载时,利用荷载分组,将荷载分解为正、反对称的两组,并将他们分别作用于结构上求解内力,然后将计算结果叠加。
反对称正对称在计算对称结构时,根据对称结构特性,可以选取半个结构计算。
选取半结构的原则:1、在对称轴的截面或位于对称轴的节点处2、按原结构的静力和位移条件设置相应的支撑,使半结构与原结构的内力和变形完全等效奇数跨对称结构:偶数跨对称结构:在用位移法求解超静定结构的时候,同样可以利用对称性简化计算。
分析可知,在正对称荷载时用位移法求解只有一个基本未知量;但在反对称荷载时若用位移法求解将有两个基本未知量,而用力法求解则只有一个未知量。
结构力学学习心得体会浅谈对称性在结构力学中的应用 摘要:在工程实际问题中,有很多结构都具有对称性。
我们对这些结构进行受力分析的时候,常常将结构简化为杆系模型,而结构力学研究的就是结构的杆系模型,因此对称性在结构力学中有着广泛的应用。
特别是在求解超静定结构问题中,无论力法还是位移法,都是繁杂的.但对于对称结构,利用结构的对称性,可使结构内力计算大为简化.现在本文章就对称性在结构力学中的应用做一简单的总结。
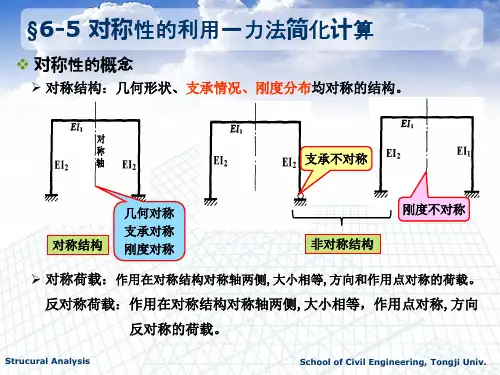
关键词:结构力学;对称性;内力;变形1.引言所谓对称结构是指几何形状和支承对某一对称轴对称.且杆件截面和材料性质也对此轴对称。
利用结构的对称性可使计算得到简化,这是因为对称结构具有如下特点:在正对称荷载作用下,内力和变形是正对称的;在反对称荷载作用下,内力和变形是反对称的,如下图所示:2.对称性在求解结构内力中的应用对称结构在正对称荷载作用下,其对称的内力(弯矩和轴力)和位移是正对称的,其反对称的内力(剪力)是反对称的;在反对称荷载作用下,其对称的内力(弯矩和轴力)和位移是反对称的,其反对称的内力(剪力)是正对称的。
因此,只要我们做出半边结构的内力图,也就知道了整个结构的内力图。
据此,我们在对对称结构进行内力分析时,就可以取半边结正 对 称 反 对 称构进行分析。
取半边结构进行分析,可以减少超静定次数,减少基本未知量,为解题提供了很大的方便。
在用力法解决超静定问题时,对于对称的结构,可利用对称性简化计算。
简化步骤如下:①选取对称的基本结构。
②将未知力及荷载分组。
③取半结构进行计算。
对于对称结构承受一般非对称荷载时,利用荷载分组,将荷载分解为正、反对称的两组,并将他们分别作用于结构上求解内力,然后将计算结果叠加。
在计算对称结构时,根据对称结构特性,可以选取半个结构计算。
选取半结构的原则:(1)在对称轴的截面或位于对称轴的节点处(2)按原结构的静力和位移条件设置相应的支撑,使半结构与原结构的内力和变形完全等效.奇数跨对称结构:偶数跨对称结构:例如下图(a)所示,此二层刚架为对称结构承受对称荷载,沿对称轴断开,取半结构如图(b)所示.原六个位移基本未知量转为两个基本未知量、并注意半结构粱抗弯刚度相应增大为原二倍即建立结点A、C力矩平衡方程,可解出,M 图如图(c)所示。