单跨静定梁

FSK
ql 2
qx
cos
0
x
l
FNK
FAy sin
qx sin 0
FNK
ql 2
qx
sin
0
x
l
③作内力图
MK
ql 2
x
qx2 2
0
x
l
FSK
ql 2
qx
cos
0
x
l
ql sinFNKFra bibliotekql 2
qx
sin
0
x
l
2
ql 2 M图 8
ql cos 2
➢将斜梁与相应水平梁作比较：
q 'l
q 'l
2
2
q 'l tan 2
q 'l2
M图 8cos
FS图
q 'l tan
2
FN图
总结斜梁内力分析的特点：
➢截面内力的计算：截面法 ➢沿水平向布置的竖向荷载作用下，简支斜梁的支座反力和相应水平梁的
支座反力相同，弯矩图相同 ➢沿水平向布置的竖向荷载作用下，斜梁的剪力和轴力是相应水平梁剪力
13.805kN
M max 13.805kN.m
单选题 1分
静定结构在荷载作用下均会产生内力，而且内力大小与杆件截面尺 寸及截面材料均无关。
A 正确 B 错误
提交
四、 简支斜梁的计算 1、斜梁应用：楼梯、屋面斜梁、及具有斜杆的刚架结构中
简支斜梁
2、斜梁所受分布荷载
q q' A
沿水平方向均布荷 载q：活载（人群、 雪载）
Fy 0 FA 10 10 4 33.75 10 2 0 FA 36.25kN ()

浅述单跨静定梁弯矩图的快速绘制摘要：梁是结构的主要受力单元，在计算梁的承载及破坏时，弯矩图的作用至关重要。

而弯矩图的绘制是学生在学习的一个弱点，因此针对静定粱结构的弯矩图快速绘制进行探讨，可以大大提高作图速度和效率。

关键词：静定梁弯矩弯矩图引言：力学课程是工科专业学生的一门必不可少的基础课程，它对于后续钢筋混凝土等课程的学习起十分重要的作用。

就建筑本身来说，就是一个力学模型，要保证结构的安全就必须确保每个受力构件的计算准确。

因此学好力学课程有非常重要的意义，而在日常力学课程的学习中，梁的弯矩图绘制却是学生在学习中的难点，文章通过总结各种弯矩图绘制的方法后，给出一种能够较为快速的绘制弯矩图的方法，对于梁的后续计算打下基础。

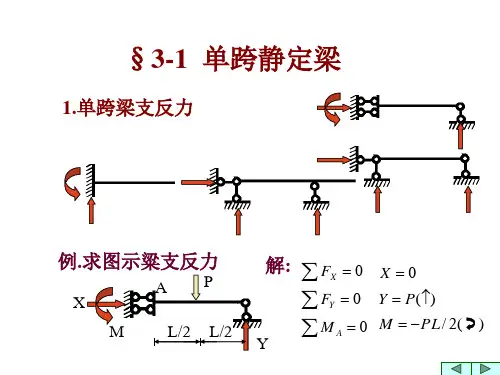
1理论知识1、1 单跨静定梁的种类（如图1）：（a)悬臂梁(b)简支梁(c) 外伸梁[1]图1 ：单跨静定梁的种类(Figure 1: The single-span beam statically determinate types)1、2弯矩出现的原因：弯矩伴随梁的弯曲变形而出现1、3弯矩的位置：弯矩出现在梁的截面上1、4弯矩的正方向规定：弯矩使梁的下侧（以梁的轴线为分界）纤维受拉为正1、5弯矩计算的基本方法：利用截面法计算，通过分段列弯矩图的函数表达式求解1、6 弯矩图绘制的方法：先绘制梁的轴线，弯矩图绘制在梁的受拉侧，不需要标明正负号2静定梁弯矩图绘制的实用结论2、1 弯矩的本质：弯矩是为了平衡所有外界力对截面的转动效果2、2弯矩分段的位置：弯矩作为内力的一种，与外力作用密切相关。

因此，绘制梁的弯矩图时，在有外力（）作用的位置分段进行[2]2、3 需要求解弯矩的截面位置：通常出现在梁的两端以及分段位置的截面处2、4 弯矩图形的特点：梁上的荷载分为四种情况：无荷载区段、均布荷载区段、集中力作用点和集中力偶作用点。

可以对梁的弯矩图特点总结出以下规律（如表1）：2、4、1、当某段梁上无分布荷载（无荷载区段），即时，是与无关的常数，是的一次函数。

FAy
1 3a 4 FP a M q 3a 3a 2 5
第三章
静定结构的内力计算
M
B
0
3a 4 FAy 3a M q 3a FP a 0 2 5 1 3a 4 FAy FP a M q 3a 3a 2 5
第三章
无荷载 平行轴线
Q图
静定结构的内力计算
均布荷载
集中力 发生突变
P
集中力偶
无变化 发生突变
m
斜直线
M图
二次抛物线 凸向即q指向
出现尖点
两直线平行 备 注
Q=0区段M图 Q=0处，M 平行于轴线 达到极值
集中力作用截 集中力偶作用 面剪力无定义 面弯矩无定义
在自由端、铰支座、铰结点处，无集中力偶作用，截面弯矩 等于零，有集中力偶作用，截面弯矩等于集中力偶的值。
第三章 静定结构的内力计算
第三章
静定结构的内力计算
§3-1单跨静定梁
一、静定结构概述 1．概念：是没有多余约束的几何不变体系。 2．特点：在任意荷载作用下，所有约束反力和内力都 可由静力平衡方程唯一确定。 平衡方程数目 = 未知量数目 3．常见的静定结构 常见的静定结构有：单跨静定梁、多跨静定梁、静 定平面刚架、三铰拱、静定平面桁架、静定组合结构等 (如下图）。
0 FYA FYA 0 FYB FYB
A
x
C
L
斜梁的反力与相应简支 梁的反力相同。
第三章
（2）内力
静定结构的内力计算
求斜梁的任意截面C的内力，取隔离体AC： a FP1 A
FYA x Fp1 FYA
0
MC

以例说明如下
例 绘制刚架的弯矩图。 解：
E 5kN
由刚架整体平衡条件 ∑X=0 得 HB=5kN← 此时不需再求竖向反力便可 绘出弯矩图。 有：
30
20 20 75 45
40
0
MA=0 , MEC=0 MCE=20kN· m（外） MCD=20kN· m（外） MB=0 MDB=30kN· m（外） MDC=40kN· m（外）
有突变
铰或 作用处 自由端 (无m）
m
Q图
M图
水平线
⊕
⊖㊀
Q=0 处 突变值为P 如变号 无变化
有极值 尖角指向同P 有极值 有突变 M=0 有尖角
斜直线
→
↑
利用上述关系可迅速正确地绘制梁的内力图（简易法）
简易法绘制内力图的一般步骤：
（1）求支反力。 （2）分段：凡外力不连续处均应作为分段点， 如集中力和集中力偶作用处，均布荷载两端点等。 （3）定点：据各梁段的内力图形状，选定控制 截面。如集中力和集中力偶作用点两侧的截面、均 布荷载起迄点等。用截面法求出这些截面的内力值， 按比例绘出相应的内力竖标，便定出了内力图的各 控制点。
说明：
（a）M图画在杆件受拉的一侧。 （b）Q、N的正负号规定同梁。Q、N图可画在杆的 任意一侧，但必须注明正负号。 （c）汇交于一点的各杆端截 面的内力用两个下标表示，例如： MAB表示AB杆A端的弯矩。 MAB
例 作图示刚架的内力图
RB↑
←HA
VA→
CB杆：
由∑ X=0 可得： M = CD RB=42kN↑ HA=48kN←， H （左） A=6×8=48kN← 由∑M144 VA=22kN↓ 48 A=0 可得： MEB=MEC=42×3 ↑ （2）逐杆绘M图 R=126kN = 126 · m （下） B 192 MDC=0 CD杆： M =42 × 6-20 × 3 由 ∑Y=0 可得： CB MCD=48kN·m（左） =192kN· m（下） VA=42-20=22kN↓

２、截面法 若要求某一横截面上的内力，假想用一平面沿杆轴垂直方向将该 截面截开，使结构成两部分；在截开后暴露的截面上用力（内力）代 替原相互的约束。
对于截开后结构的两部分上，截面上的内力已成为外力，因此，
由任一部分的静力平衡条件，均可列出含有截面内力的静力平衡方程。 解该方程即将内力求出。
３、截面内力 截开一根梁式杆件的截面上有三个内力（分量），即：轴力ＦN 、 剪力ＦQ和弯矩Μ 。
dFN/dx=-qx
dFQ/dx=-qy dM/dx=Q
d2M/dx2=-qy
增量关系： DFN=-FPx
DFQ=-FPy
DM=m
１）微分关系及几何意义： dFN/dx=-qx dFQ/dx=-qy dM/dx=Q d2M/dx2=-qy （１）在无荷载区段，ＦQ图为水平直线；
当ＦQ≠０时，Μ图为斜直线;
右右为正。
ＦQ＝截面一侧所有外力在杆轴垂直方向上投影的代数和。左上为正， 右下为正。
Μ ＝截面一侧所有外力对截面形心力矩代数和。弯矩的竖标画在杆
件受拉一侧。
例3-1-1 求图（a）所示简支梁在图示荷载下截面的内力。
解：1）支座反力 ∑ΜA=0 FBy×4﹣10×4×2﹣100× (4/5)×2=0 Fby=60kN (↑) ∑ΜB=0 FAy=60kN (↑) ∑Fx= 0 FAx+100×(3/5)=0 FAx=－60kN (← ) 由 ∑Ｆy= 0 校核，满 足。
(下侧受拉)
区段叠加法求Ｅ、Ｄ截面弯矩； ΜE＝20×42/8＋120/2＝100kNm ΜＤ＝40×4/4＋120/2＝100kNm
(下侧受拉) (下侧受拉)
内力应考虑
说明：集中力或集中力偶作用点，注意对有突变的 分两侧截面分别计算。

工程中，斜梁和 斜杆是常遇到的，如楼梯梁、刚架中的斜梁等。斜梁 受均布荷载时有两种表示方法： （1）按水平方向分布的形式给出（人群、雪荷载等），用 q 表示。 （2）按沿轴线方向分布方式给出（自重、恒载），用 q’ 表示。
q 与 q’间的转换关系：
qdx qds q q
cos
第3章
[例题] 试绘制图示斜梁内力图。
q
B
C
A
α
D VB
HA
l/3 l/3
l/3
VA
（1）求支座反力：
解：
X 0 MB 0 MA 0
HA 0
VA
ql 6
()
VB
ql 6
()
校核：
Y
qj 6
qj 6
ql 3
0
第3章
（2）AC段受力图：
（3）AD段受力图：
HAcosα HAsinα
HA VAsinα
VA VAcosα
MC
C
NC
α QC
HAcosα
dx
d2M dx2
q(x)
（1）在无荷区段q(x)＝０，剪力图为水平直线，弯矩图为斜直线。
（2）在q(x)＝常量段，剪力图为斜直线，弯矩图为二次抛物线。其凹下去的曲 线象锅底一样兜住q(x)的箭头。
（3）集中力作用点两侧，剪力值有突变、弯矩图形成尖点；集中力偶作用点两 侧，弯矩值突变、剪力值无变化。
解：
10KN/m A HA=0
4m VA=26.25kN
30KN.m
20KN
C
D
B
E
2m
2m
32.5 2.5
3m VB=33.75KN 60
（1）计算支座反力

（二）绘内力图：
H A
=0
V
A =130KN
X 0 Y 0 M 0
C
NC 0 QC 130 KN M C 130 KN .M
第3章 例题: 试绘制图示外伸梁的内力图。
解：
10KN/m A HA=0 4m C 2m D B E 30KN.m 20KN
（1）计算支座反力
2m
2kN E
2m F
F
2m
G 2kN
2m
（b）
A
4kN/m B
C
G 2kN
G
B
11kN 4
4kN
4
（d）
8 7
（e） 9
4 M（kN.m） 2 2
Q（kN）
2
第3章 例题2： 图示三跨静定梁，全长承受均布荷载q，试确定铰E、F的位置，使中 间一跨支座的负弯矩与跨中正弯矩数据数值相等。
第3章
3.3 静定平面刚架的内力计算 一、刚架的组成 1、刚架的特征 由若干梁和柱用刚结点联结而成的结构。具有刚结点是 刚架的主要特征。 2、刚架的应用 刚架在工程上有广泛的应用。
（1）斜梁的倾角为常数，而曲梁各截面的的倾角是变量。 （2）计算曲梁的倾角时，可先写出曲梁的轴线方程y=f(x),而后对x求一 阶导数，进而确定倾角：
dy tan ; dx
tan1 (tan )
（3）角以由x轴的正方向逆时针转到切线方向时为正，反时针方向为负。
例题：试求图示曲梁C截面的内力值。已知曲梁轴线方程为：
y 4f 4 4 (l x) x 2 (12 1.5) 1.5 1.75m l2 12
4f 4 4 tan yx 1.5 2 (l 2 x) x1.5 2 (12 2 1.5) 1 l 12 2 450 sin con 0.707 2

l
l/2 l/2
MM
l
l
练习: 利用微分关系等作弯矩图
M
1 ql2 2
P 1 ql2
4
l
l/2 l/2
l
M
2M
MM
l
l
lM
M
l
练习: 利用微分关系等作弯矩图
1 ql2 2
P 1 ql2
4
q
1 ql2
l
l/2 l/2
2l
l
M
2M
M
MM
M
M
M
M MM
M
l
l
MM
练习: 利用微分关系,叠加法等作弯矩图
M图
Q图
例: 作内力图
铰支座有外 力偶,该截面弯矩 等于外力偶.
M图 Q图
无剪力杆的 弯矩为常数.
M图
自由端有外
力偶,弯矩等于外
Q图 力偶
练习: 利用上述关系作弯矩图,剪力图
练习: 利用上述关系作弯矩图,剪力图
5.叠加法作弯矩图
注意:
是竖标相加,不是 图形的简单拼合.
练习:
1 ql2 16
种结构型式?
简支梁(两个并列) 多跨静定梁
连续梁
例.对图示静定梁,欲使AB跨的最大正弯矩与支座B截
面的负弯矩的绝对值相等,确定铰D的位置.
q
A
D
B
C
x
l
l
RD
q
q(l x)2 / 8
RD
B
解: RD q(l x) / 2()
M B qx2 / 2 q(l x)x / 2 q(l x)2 / 8 qx2 / 2 q(l x)x / 2

静力法绘制单跨静定梁的影响线根据影响线的定义,我们将单位集中荷载F=1作用于结构的任意位置,并选定一坐标系,以横坐标x表示单位集中荷载的作用位置,由静力平衡条件求出结构的某量值与单位集中移动荷载的作用位置x的函数关系,此关系式称为影响线方程。

根据影响线方程绘出影响线图形,这种绘制影响线的方法称为静力法。

1)简支梁的影响线(1)反力影响线设要绘制如图17.3(a)所示简支梁反力FAy的影响线。

取支座A为原点,梁轴线AB为x轴,向右为正,以坐标x表示单位集中荷载F=1的作用位置。

当F=1移动到梁上的任意位置(0≤x≤l)时,取全梁为研究对象,画其受力图,并设反力向上为正,由静力平衡条件图17.3则有得此式即为反力FAy 的影响线方程。

由此可见,FAy将随x的变化而变化,并且是x的一次函数,因此FAy的影响线是一条直线段,只需要确定两点即可画出该直线段:当x=0时,FAy=1当x=l时,FAy=0将这两点用直线相连,即可绘制出FAy的影响线,如图17.3(b)所示。

绘制影响线时,常规定正的竖标画在基线的上侧,负的竖标画在基线的下侧,并要标注正负号。

在此必须强调,FAy的影响线图中所有的竖标代表的是当F=1作用在相应位置处时,反力FAy 的大小。

例如图17.3(b)中的yK代表的是当F=1作用在K位置处时反力FAy的大小。

同理,对于反力FBy,由静力平衡条件,则有FByl-Fx=0即可列出FBy的影响线方程显然也是x的一次函数,因此FBy的影响线同样是一直线段,只需要确定两点:当x=0时,FBy=0当x=l时,FBy=1即可绘制出FBy的影响线,如图17.3(c)所示。

由于F=1的量纲为1,所以反力影响线竖标的量纲也为1。

今后在利用影响线研究实际荷载的影响时,应乘以实际荷载的相应单位。

(2)剪力影响线现绘制如图17.4(a)所示简支梁截面C的剪力FQC影响线。

仍取A点为坐标原点,x表示单位集中荷载F=1的作用位置。

FA
FB
ql 2
()
(2)列剪力方程和弯矩方程
FS (x)
FA
qx
1 2
ql
qx
(0< x l)
M (x)
FA x
1 2
qx 2
1 2
qlx
1 2
qx 2
(0 x l)
(3) 绘制剪力图和弯矩图
两端支座处： 梁跨中：
ql FSmax 2
M max
ql 2 8
q
A C
x
FA
l
1 ql
2
1 ql 2 8
剪力为常数，FS图为
平直线；弯矩为一次
FaFS图FS图(b) (b) 函数，M图为斜直线。
l
Fa
M图
l (c)
M图 (c)
集中力F处，剪力图 发生突变，弯矩图
有尖角。
单跨静定梁的内力图
2.单一荷载下静定梁的内力图
A
解：(1)求支座约束力
FA
由梁的整体平衡条件可求得：
M l
e
()
FA
(2)列剪力方程和弯矩方程
单跨静定梁的内力图
1. 剪力方程和弯矩方程 为了形象地表示剪力和弯矩沿梁轴线变化的规律，以沿梁轴线的横坐标x表示梁横
截面的位置，以纵坐标表示相应横截面上的剪力或弯矩，按剪力方程和弯矩方程绘出 图形，这种图形分别称为剪力图和弯矩图，即梁的内力图。
剪力方程
FS FS (x)
正剪力画在x轴上方负 剪力画在x轴下方,并在
图中标明“ ”、x轴下方负 剪力画在x轴上方,并在
图中标明“ ”、“ ”。
单跨静定梁的内力图
2.单一荷载下静定梁的内力图

(d)
M M M FQdx m 0
M m
(e)
以上两式，为荷载与内力的增量 关系。式(e)忽略了一阶微量。
增量关系的几 何意义
在集中力作用点（集中力垂直 与杆轴或有垂直于杆轴的分量） 两侧截面，剪力有突变，突变 值即为该集中力或垂直于杆轴 的分量；弯矩相同。
在集中力偶作用截面两侧，弯矩 有突变，突变值即为该集中力偶； 剪力相同。
a
M
0
M1
1 2
qa 2
FAy a
M
用文字写 明受拉侧
取截面1右侧为隔离体 计算可得同样结果
3.直接法求指定 截面的内力
由例3-1-1内力计算结果 分析，指定截面的内力可 用该截面一侧的外力直接 表示，即：
轴力 （FN）
截面一侧所有外力在指定 截面法线方向投影的代数 和，以与截面外法线方向 相反为正。
剪力 （FQ）
截面一侧所有外力在指定 截面切线方向投影的代数 和，左上、右下为正。
弯矩（M）
截面一侧所有外力对 指定截面形心力矩的 代数和。
例3-1-2 用直接法，求例 3-1-1图(a)所示伸臂梁截 面2上的内力。
M
(a)
解
支座反力计算同例3-1-1。内力 可由右图所示受力图直接计算：
M
F A x F A y
3a 2
FP
4 5
a
(↓)
（箭头标出 实际方向）
MA 0
FBy
3a
M
q 3a
3a 2
FP
4 5
4a
0
(↑) FBy
1 M 3a
q 3a
3a 2
FP
4 4a 5
箭头标出实 际方向

§3-2 多跨静定梁
例3-4 试作图a所示多跨静定梁的内力图，并求出各支座反力。
解：不算反力 先作弯矩图
1）绘AB、GH段弯矩图，与悬臂梁相同； 2）GE间无外力，弯矩图为直线，MF=0，可绘出； 同理可绘出CE段； 3）BC段弯矩图用叠加法画。
§3-2 多跨静定梁
由弯矩与剪力的微分关系画剪力图
由若干根梁用铰相联，并用若干支座与基础相联而组成的静定结构。
分析多跨静定梁的一般步骤
对如图所示的多跨静定梁，应先从附属部分CE开始分析：将 支座C 的支反力求出后，进行附属部分的内力分析、画内力图， 然后将支座 C 的反力反向加在基本部分AC 的C 端作为荷载，再 进行基本部分的内力分析和画内力图，将两部分的弯矩图和剪力 图分别相连即得整个梁的弯矩图和剪力图 。
弯矩图为直线：其斜率为剪力。图形从基线顺时针转，
剪力为正，反之为负。 弯矩图为曲线：根据杆端平衡条件求剪力，如图c。
剪力图作出后即可求支座反力 取如图e的隔离体可求支座 c— 的反力 弯矩—剪力 支座反力
§3-3 静定平面刚架
常见静定刚架的型式
悬臂刚 架
简支刚 架
三铰刚 架
§3-3 静定平面刚架
R FSR F E SD 8kN
FSR F 12kN
FSR B 0
§3-1 单跨静定梁
用截面法计算 控制截面弯矩。
MC 0
M A 20kN 1m 20kN m
M D 20kN 2m 58kN 1m 18kN m M E 20kN 3m 58kN 2m 30kN 1m 26kN m M F 12kN 2m 16kN m 10kN m 18kN m

F
G
7 kN
R M F = 7 KN m R FQF = -7 KN
R FQF
F
G
7 kN
MG
FQG
G
MG = 0 FQG = -7 KN
7 kN
A 弯矩M 0
BL 17
BR 17
C 26
E 30
FL 23
FR 7
G 0
剪力FQ
17
17
9
9
-7
-7
-7
-7
Step3:绘制内力图。
A B C D E F 7 G
荷载 无荷载
内力 P m A
l
a b
l
P
FQ
FQ = 常量 斜直线
斜直线
FQ = 常量 无变化
m
M
ql 2 8
Pab l
M =0
绘制内力图技巧： ① 集中Px作用，FN图发生突变 ② 集中Py作用，FQ图发生突变，导致M图斜率改变，出 现尖点；且尖角的朝向与荷载的方向相同。 ③ 集中m作用，M图发生突变，FN、FQ图无变化 在绘制和校核内力图时十分有用。适用于受弯构件。
(3 - 1)
四．荷载与内力之间的增量关系
M
M0 Fx O Fy
M M
FN FN
FN
FQ
x
dx
FQ FQ
y 由平衡条件可导出增量关系如下（Fx为水平集中力； Fy为竖向集中 力； Mo为力偶。）：
FN = - Fx FQ = - Fy M = M 0
(3 - 2)
FQ
FN
＋
FQ
FN FN
FQ
－
FQ
FN

第二节 单跨静定梁一、单跨静定梁的内力分析单跨静定梁通常有三种基本形式，即简支梁(图3-7(a))、悬臂梁(图3-7(b))和外伸梁（图3-7(c)），还有如图3-7(d)所示简支斜梁以及如图3-7(e)所示曲梁。

这些梁支座反力都只有三个，可取全梁段为隔离体，由三个整体平衡方程先行求出。

图3-7 单跨静定梁的形式(a)简支梁 (b)悬臂梁 (c)外伸梁 (d)简支斜梁 (e)曲梁根据上一节所述的截面法、内力图的形状特征和区段叠加法作弯矩图，可将单跨静定梁内力图的绘制步骤归纳如下：（1）利用整体平衡条件求支座反力（悬臂梁可不求支座反力）；（2）选定外力的不连续点 (如支座处、集中荷载及集中力偶作用点左右截面、分布荷载的起点及终点等) 为控制截面，采用截面法求出控制截面处的内力值；（3）根据内力图的形状特征，直接作相邻控制截面间的内力图。

如果相邻控制截面间有横向荷载作用，其弯矩图应采用区段叠加法来绘制。

【例3-1】作图3-8(a)所示两端外伸梁的内力图。

【解】：（1）求支座反力取全梁为隔离体，由0=∑A M ，即：810210423010290B F ⨯+⨯-⨯⨯--⨯⨯=,得：33.75()B F kN =↑。

再由0y F =∑，得：36.25()A F kN =↑。

A 支座的水平方向支座反力为零。

（2）绘制剪力图先采用截面法求下列各控制截面的剪力值。

SD 101036.2526.2510233.7513.7510220R L SA R SA L SC SB R SB F F kNF kNF F kNF kN ==-=-+===⨯-=-=⨯=然后根据剪力图的形状特征绘出剪力图，如图3-8(b)所示。

（3）绘制弯矩图先采用截面法求出下列控制截面处的弯矩值。

图3-8 例3-1图(a)外伸梁计算简图 (b)S F 图（kN ）(c)M 图（kN.m ）010220(.)()106104236.2545(.)()108104436.25622.5(.)()102333.7527.5(.)()102120(.)()0D A C LE R E BF M M kN m M kN m M kN m M kN m M kN m M ==-⨯=-=-⨯-⨯⨯+⨯==-⨯-⨯⨯+⨯=-=-⨯⨯+⨯==-⨯⨯=-=，上拉下拉上拉下拉上拉，然后根据弯矩图的形状特征直接作DA 段、CE 段、EB 段的弯矩图，采用区段叠加法作AC 段、BF 段的弯矩图，如图3-8(c)所示，弯矩图画在受拉侧。

A
FP
B
FQห้องสมุดไป่ตู้B
FQBA
（2）杆端内力正负规定
杆端弯矩：对杆端一侧顺时针为正
对支座、结点一侧逆时针为正 MAB<0
A
FP
MBA >0
，
B
MAB<0
A
FP
MBA>0
B
（2）杆端内力正负规定
杆端弯矩：对杆端一侧顺时针为正
对支座、结点一侧逆时针为正 杆端剪力：与材料力学规定相同 FQAB >0
A
FQAB >0
载 载 载
载
1
形 形 载
载 载 载
载 形 载
载
单跨超静定梁在荷载和支座移动共同作 用下
FP
x
y
在线性小变形条件下，由叠加原理可得
4：转角位移方程
6i F M 4 i 2 i M AB A B AB AB l M 4 i 2 i 6 i M F BA B A AB BA l
转角位移方程(刚度方程)
EI 其中： i 称杆件的线刚度。 l F F 为由荷载引起的杆端弯矩， M AB , M BA 称为固端弯矩。
Fab 2 l
A
2
反弯点
C
a F
D
EI b l
Fab 2 l
2
C
F
拐点 D
EI
B A
B
弯矩图
Fb2 (l 2a ) F 3 l
A a EI b l B
变形曲线
Fa2 (l 2b) 3 l
剪力图
§5-7 等截面单跨超静定梁杆端内力
一、单跨超静定梁的概念 1：基本的单跨超静定梁类型 2：杆端内力（大小，转向） 3：形常数、载常数、线刚度 4：转角位移方程 二、学会查表计算杆端内力

§5.2 单跨静定梁的三种基本形式
简支梁、悬臂梁和外伸梁为工程中常见静定梁的三种基本形式。

实际工程中，梁的受力和支座情况都比较复杂。

为了便于分析和计算，需要进行简化，并由此得到梁的计算简图。

梁的简化通常是从梁的结构、支座和荷载等三方面进行。

一、梁的结构简化
梁是具有一定高度和宽度的构件。

在简化时，通常用梁的轴线来代表梁的实体，支座间的距离称为计算跨度。

图5-2
如图5-2(b)所示，用轴线AB代表起重吊车的横梁。

二、支座简化
常见支座形式有三种：可动铰支座、固定铰支座和固定端支座。

梁的实际支座的简化，主要根据每个支座对梁的约束情况来定。

例如图5-2(a)中起重吊车的横梁可简化为一端为可动铰支座，另一端为固定铰支座的梁。

如图5-2(b)所示。

三、荷载简化
作用于梁上的荷载通常可简化为集中力、集中力偶和分布荷载等。

如图5-4所示：
图5-4
通过上述三方面简化即可得到梁的计算简图。

工程中常见单跨静定梁有三种基本形式。

简支梁：一端为固定铰支座，另一端为可动铰支座的梁。

如图5-5(a)所示。

图5-5
悬臂梁：一端为固定端支座，另一端为自由端的梁。

如图5-5(b)所示。

外伸梁：一端或两端伸出支座外的简支梁。

如图5-5(c)所示。

第十章静定结构的内力分析本章主要讨论静定结构的内力计算。

它不仅是静定结构位移计算的基础，而且也是超静定结构计算的基础。

第一节静定梁的内力一、单跨静定梁单跨静定梁的力学简图有简支梁、悬臂梁和外伸梁三种形式，如图11-1所示。

图11-1梁内任意截面的内力的计算方法、内力图及弯矩图的做法在本书第六章中已有详细介绍，在此不再详述。

二、多跨静定梁若干根梁用铰相连，并和若干支座与基础相连而组成的静定梁，称为多跨静定梁。

在实际的建筑工程中，多跨静定梁常用来跨越几个相连的跨度。

图10-2(a)所示为一公路或城市桥梁中，常采用的多跨静定梁结构形式之一，其计算简图如图10-2(b)所示。

在房屋建筑结构中的木檩条，也是多跨静定梁的结构形式，如图10-3(a)所示为木檩条的构造图，其计算简图如图10-3(b)所示。

连接单跨梁的一些中间铰，在钢筋混凝土结构中其主要形式常采用企口结合(图10-2a)，而在木结构中常采用斜搭接并用螺栓连接(图10-3a)。

图10-2 图10-3从几何组成分析可知，图10-2(b)中AB梁是直接由链杆支座与地基相连，是几何不变的。

且梁AB本身不依赖梁BC和CD就可以独立承受荷载，称之为基本部分。

如果仅受竖向荷载作用，CD梁也能独立承受荷载维持平衡，同样可视为基本部分。

短梁BC是依靠基本部分的支承才能承受荷载并保持平衡，所以，称为附属部分。

同样道理在图10-3(b)中梁AB、CD和EF均为基本部分，梁BC和梁DE为附属部分。

为了更清楚地表示各部分之间的支承关系，把基本部分画在下层，将附属部分画在上层，如图10-2(c)和图10-3(c)所示，我们称它为关系图或层叠图。

计算多跨静定梁时，必须先从附属部分计算，再计算基本部分，按组成顺序的逆过程进行。

例如图10-2(c)，应先从附属梁BC计算，再依次考虑AB、CD梁。

这样便把多跨梁化为单跨梁，分别进行计算，从而可避免解算联立方程。

再将各单跨梁的内力图连在一起，便得到多跨静定梁的内力图。