第21课时-二次函数与方程(组)或不等式(附答案)

第21讲不等式的基本性质作者：刘族刚来源：《高中生学习·高三文综版》2014年第10期考情分析不等式的基本性质与一元二次不等式式不等式是高中数学的重要内容和基础内容，是分析、解决有关数学问题的基础与工具，也是高考考查的重点，在近几年高考中，有关不等式的试题都占有较大的比重，考查内容中不仅有不等式的基本性质、二次不等式的求解、求证、恒成立问题，而且容易与集合问题、二次方程和二次函数、三角、数列、复数、立体几何、解析几何等进行综合，形成中档或难题.命题特点不等关系常伴随函数、数列、立体几何、解析几何或实际问题进行考查，高考中考查不等式的性质多以选择、填空形式出现.而对于一元二次不等式，一般采用以下两种形式考查：一是考查一元二次不等式的解法及其“三个二次”间的关系问题，二是以函数、导数为载体，考查不等式的参数范围问题.1. 比较代数式（值）的大小例1 已知[x，y∈R]，比较[x2-xy+y2]和[x+y-1]的大小.解析 [（x2-xy+y2）-（x+y-1）] [=（x2-x）+（y2-y）-xy+1][=12（2x2-2x+2y2-2y-2xy+2）][=12（x2-2x+1+y2-2y+1+x2+y2-2xy）][=12[（x-1）2+（y-1）2+（x-y）2]].∵[（x-1）2≥0]，[（y-1）2≥0]，[（x-y）2≥0]，∴[12[（x-1）2+（y-1）2+（x-y）2]≥0].∴[x2-xy+y2≥x+y-1].点拨作差比较法基本步骤：作差，变形，判断差的符号，结论.其中判断差的符号为目的，变形是关键，常用变形技巧有因式分解，配方，拆、拼项等方法.2. 不等式性质的应用例2 对于实数[a ，b ，c]，判断以下命题的真假.（1）若[a>b]，则[ac>bc]；（2）若[ac2>bc2]，则[a>b]；（3）若[aab>b2]；（4）若[a|b|]；（5）若[a>b]，则[ab>1]；（6）若[a>b]且[1a>1b]，则[a>0 ，b（7）若[a>b]，则[a3>b3]；（8）若[a>b]，则[|a|>b].解析（1）因为[c]的符号不定，所以无法判定[ac]和[bc]的大小，故原命题为假命题.（2）因为[ac2>bc2]，所以[c≠0]，从而[c2>0]，故原命题为真命题.（3）①因为[aab.]②又[ab2].综合①②得[a2>ab>b2]，故原命题为真命题.（4）两个负实数，绝对值大的反而小.故原命题为真命题.（5）当[b≤0]时，[ab>1]不成立，故原命题为假命题.（6）因为[a>b，1a>1b，⇒a-b>0，1a-1b>0，⇒b-a0，]所以[ab又因[a>b]，所以[a>0，b（7）因为[y=x13]的函数在[R]上单调递增，故原命题为真命题.（8）因为[a≥a，a>b]，所以[a>b]，故原命题为真命题.点拨判定不等式成立与否，应紧扣不等式性质，当出现字母代数式时常用赋值法.3. 不等关系在实际问题中的应用例3 甲乙两车从[A]地沿同一路线到达[B]地，甲车一半时间的速度为[a]，另一半时间的速度为[b]；乙车用速度为[a]行走一半路程，用速度[b]行走另一半路程，若[a≠b]，试判断哪辆车先到达[B]地.解析设从[A]到[B]的路程为[S]，甲车用的时间为[t1]，乙车用的时间为[t2]，则[t12a+t12b=S，][∴t1=2Sa+b，t2=S2a+S2b=S2（1a+1b）]，[∵2Sa+b-S21a+1b=2Sa+b-（a+b）S2ab] [=4abS-（a+b）2S2ab（a+b）=-（a-b）2S2ab（a+b）所以甲车先到达[B]地.4. 二次不等式的解法例4 设不等式[x2-2ax+a+2≤0]的解集为[M]，如果[M⊆[1，4]]，求实数[a]的取值范围.解析 [M⊆[1，4]]有三种情况：其一是[M=∅]，此时[Δ0]与[Δ=0]，所以分三种情况计算[a]的取值范围.设[f（x）=x2-2ax+a+2]，∴[Δ=（-2a）2-（4a+2）=4（a2-a-2）=4（a+1）a-2）].（1）当[Δ（2）当[Δ=0]时，[a=-1]或[2].若[a=-1]，则[M=-1⊈][[1，4]].若[a=2]，则[M=2⊆[1，4]].（3）当[Δ>0]时，[a2].设方程[f（x）=0]的两根[x1，x2]，且[x1那么[M=[x1，x2]]，[M⊆[1，4]]，[⇔][1≤x10，]即[-a+3>0，18-7a>0，a>0，a2，]解得，[2综上，[M⊆[1，4]]时，[a]的取值范围是[（-1，187]].点拨本题表面上是解二次不等式，实质上是二次方程的区间根问题，充分考虑二次方程、二次不等式、二次函数之间的内在联系是关键所在.5. 二次不等式恒成立问题例5 设函数是定义在[（-∞，+∞）]上的增函数，如果不等式[f（1-ax-x2）解析 [∵f（x）]是增函数，[∴f（1-ax-x2）[⇔1-ax-x2[⇔x2+ax+1-a>0]对于任意[x∈[0，1]]恒成立.令[g（x）=x2+ax+1-a]，[x∈[0，1]]，所以原问题[⇔g（x）min>0].又[g（x）min=g（0）， a>0，g（-a2），-2≤a≤0，2， a即[g（x）min=1-a， a>0，-a24-a+1，-2≤a≤0，2， a点拨本题考查数学化归转化的数学思想：利用函数的单调性把原不等式问题转化为[1-ax-x2备考指南备考过程中，要求学生熟练掌握不等式的性质与二次不等式的基础知识方法，将数学各部分知识融会贯通，同时注重对解题方法的总结，领悟不等式作为一个工具在解决数学问题（包括实际问题）中的重要性.1. “差比较法”的依据[a>b⇔a-b>0]，其中变形是关键，常进行通分、因式分解、配方或分子（母）有理化等.2. 求代数式的范围时常用“待定系数法”，先用已知的代数式表示目标式，再利用多项式相等的法则求出参数，最后利用不等式的性质求出目标式的范围，这样才能确保范围不大不小.3. 一元二次不等式[ax2+bx+c>0][（a≠0）]的解集的确定受[a]的符号、[b2-4ac]的符号的影响，且与相应的二次函数、一元二次方程有密切联系，可结合相应的函数[y=ax2+bx+c（a≠0）]的图象，数形结合求得不等式的解集.若一元二次不等式经过不等式的同解变形后，化为[ax2+bx+c>0（或0]）的形式，其对应的方程[ax2+bx+c=0]有两个不等实根[x1，x2（x10]），则可根据“大于取两边，小于夹中间”求解集.4. “二次型”函数（不等式）中含有参数时，参数的符号影响不等式的解集；不要忘了二次项系数是否为零的情况；另外解含参数的一元二次不等式，可先考虑因式分解，再对根的大小进行分类讨论，若不能因式分解，则可对判别式进行分类讨论，分类要不重不漏.限时训练1.设[a=0.512，b=0.914，c=log50.3]，则[a，b，c]的大小关系是（）A. [a>c>b]B. [c>a>b]C. [a>b>c]D. [b>a>c]2.已知函数[f（x）=x（1+a|x|）]. 设关于[x]的不等式[f（x+a）A.[1-52，0]B.[1-32，0]C. [1-52，0⋃0，1+32]D.[-∞，1-52]3.已知[aA. [a>ab>ab2]B. [ab2>ab>a]C. [ab>a>ab2]D. [ab>ab2>a]4、设变量[x，y]满足约束条件[x+2y-5≤0，x-y-2≤0，x≥0，]则目标函数[z=2x+3y+1]的最大值为（）A.11B.10C.9D.8.55. 已知[a，b∈R，且a>b]，则下列不等式中一定成立的是（）A. [ab>1]B.[a2>b2]C.[lg（a-b）>0]D. [（12）a6.已知不等式[f（x）=ax2-x-c>0]的解集为[{x-2[A] [B] [C] [D]7.在[R]上定义运算[⊗]：[x⊗y=x（1-y）].若不等式[（x-a）⊗（x-b）>0] 的解集是[（2，3）]，则[a+b=] （）A. [1]B. [2]C. [4]D. [8]8.如果[aA. [1aC. [-ab9. 已知不等式[ax2-bx-1≥0]的解集是[-12，-13]，则不等式[x2-bx-aA.（2，3）B. [（-∞，2）∪（3，+∞）]C. [（13，12）]D. [（-∞，13）∪（12，+∞）]10.关于[x]的不等式[x2-（a+1）x+aA.[（4，5）]B.[（-3，-2）⋃（4，5）]C.[（4，5]]D.[[-3，-2）⋃（4，5]]11.不等式[x2+x-212.若[113.若不等式[x2+ax+4≥0]对一切[x∈（0，1]]恒成立，则[a]的取值范围是________.14.已知[f（x）]是定义在[R]上的奇函数.当[x>0]时，[f（x）=x2-4x]，则不等式[f（x）>x]的解集用区间表示为________.15.甲厂以[x]千克/小时的速度运输生产某种产品（生产条件要求[1≤x≤10]），每小时可获得利润是[100（5x+1-3x）]元.（1）要使生产该产品[2]小时获得的利润不低于[3000]元，求[x]的取值范围；（2）要使生产[900]千克该产品获得利润最大，问：甲厂应该选取何种生产速度？并求最大利润.16.已知[x，y]为正实数，满足[1≤lgxy≤2，3≤lgxy][≤4]，求[lg（x4y2）]的取值范围.17.解关于[x]的不等式[（1-ax）218.解关于[x]的不等式[ax2-（a+1）x+1。

2.3 二次函数与一元二次方程、不等式最新课程标准：(1)从函数观点看一元二次方程．会结合一元二次函数的图象，判断一元二次方程实根的存在性及实根的个数，了解函数的零点与方程根的关系．(2)从函数观点看一元二次不等式．①经历从实际情境中抽象出一元二次不等式的过程，了解一元二次不等式的现实意义．能借助一元二次函数求解一元二次不等式，并能用集合表示一元二次不等式的解集．②借助一元二次函数的图象，了解一元二次不等式与相应函数、方程的联系.知识点二次函数与一元二次方程、不等式的解的对应关系Δ>0Δ＝0Δ<0y＝ax2＋bx＋c(a>0)的图象ax2＋bx＋c＝0(a>0)的根有两个不相等的实数根x1，x2(x1<x2)有两个相等的实数根x1＝x2＝－b2a没有实数根ax2＋bx＋c>0(a>0)的解集{x|x<x1，或x>x2}{x|x≠－b2a}Rax2＋bx＋c<0(a>0)的解集{x|x1<x<x2}∅∅状元随笔一元二次不等式的解法：(1)图象法：一般地，当a>0时，解形如ax2＋bx＋c>0(≥0)或ax2＋bx＋c<0(≤0)的一元二次不等式，一般可分为三步：①确定对应方程ax2＋bx＋c＝0的解；②画出对应函数y＝ax2＋bx＋c的图象简图；③由图象得出不等式的解集．对于a<0的一元二次不等式，可以直接采取类似a>0时的解题步骤求解；也可以先把它化成二次项系数为正的一元二次不等式，再求解．(2)代数法：将所给不等式化为一般式后借助分解因式或配方求解，当p<q时，若(x－p)(x－q)>0，则x>q或x<p；若(x－p)(x－q)<0，则p<x<q.有口诀如下“大于取两边，小于取中间”．[教材解难]教材P50思考能．可以从2个角度来看①函数的角度：一元二次不等式ax2＋bx＋c>0表示二次函数y＝ax2＋bx＋c的函数值大于0，图象在x轴的上方；一元二次不等式ax2＋bx＋c>0的解集即二次函数图象在x轴上方部分的自变量的取值范围．②方程的角度：一元二次不等式ax2＋bx＋c>0的解集的端点值是一元二次方程ax2＋bx ＋c＝0的根．[基础自测]1．下列不等式中是一元二次不等式的是( )A．a2x2＋2≥0 B.1x2<3C．－x2＋x－m≤0 D．x3－2x＋1>0解析：选项A中，a2＝0时不符合；选项B是分式不等式；选项D中，最高次数为三次；只有选项C符合．答案：C2．不等式x(x＋1)≤0的解集为( )A．[－1，＋∞) B．[－1,0)C．(－∞，－1] D．[－1,0]解析：解不等式得－1≤x≤0，故选D.答案：D3．函数y＝17－6x－x2的定义域为( )A．[－7,1]B．(－7,1)C．(－∞，－7]∪[1，＋∞) D．(－∞，－7)∪(1，＋∞)解析：由7－6x －x 2>0，得x 2＋6x －7<0，即(x ＋7)(x －1)<0，所以－7<x <1，故选B. 答案：B4．不等式1＋2x ＋x 2≤0的解集为________．解析：不等式1＋2x ＋x 2≤0化为(x ＋1)2≤0，解得x ＝－1. 答案：{－1}题型一 解不含参数的一元二次不等式[教材P 52例1、2、3] 例1 (1)求不等式x 2－5x ＋6>0的解集． (2)求不等式9x 2－6x ＋1>0的解集． (3)求不等式－x 2＋2x －3>0的解集．【解析】 (1)对于方程x 2－5x ＋6＝0，因为Δ>0，所以它有两个实数根．解得x 1＝2，x 2＝3.画出二次函数y ＝x 2－5x ＋6的图象(图1)，结合图象得不等式x 2－5x ＋6>0的解集为{x |x <2，或x >3}．(2)对于方程9x 2－6x ＋1＝0，因为Δ＝0，所以它有两个相等的实数根，解得x 1＝x 2＝13.画出二次函数y ＝9x 2－6x ＋1的图象(图2)，结合图象得不等式9x 2－6x ＋1>0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ≠13(3)不等式可化为x2－2x＋3<0.因为Δ＝－8<0，所以方程x2－2x＋3＝0无实数根．画出二次函数y＝x2－2x＋3的图象(图3)．结合图象得不等式x2－2x＋3<0的解集为∅.因此，原不等式的解集为∅.因为方程x2－5x＋6＝0的根是函数y＝x2－5x＋6的零点，所以先求出x2－5x＋6＝0的根，再根据函数图象得到x2－5x＋6>0的解集．教材反思我们以求解可化成ax2＋bx＋c>0(a>0)形式的不等式为例，用框图表示其求解过程．跟踪训练1 解下列不等式：(1)x2－7x＋12>0；(2)－x 2－2x ＋3≥0； (3)x 2－2x ＋1<0； (4)－2x 2＋3x －2<0.解析：(1)因为Δ＝1＞0，所以方程x 2－7x ＋12＝0有两个不等实根x 1＝3，x 2＝4.再根据函数y ＝x 2－7x ＋12的图象开口向上，可得不等式x 2－7x ＋12＞0的解集是{x |x ＜3或x ＞4}．(2)不等式两边同乘－1，原不等式可化为x 2＋2x －3≤0.因为Δ＝16＞0，所以方程x2＋2x －3＝0有两个不等实根x 1＝－3，x 2＝1.再根据函数y ＝x 2＋2x －3的图象开口向上，可得不等式－x 2－2x ＋3≥0的解集是{x |－3≤x ≤1}．(3)因为Δ＝0，所以方程x 2－2x ＋1＝0有两个相等的实根x 1＝x 2＝1.再根据函数y ＝x 2－2x ＋1的图象开口向上，可得不等式x 2－2x ＋1＜0的解集为∅.(4)原不等式可化为2x 2－3x ＋2＞0，因此Δ＝9－4×2×2＝－7＜0，所以方程2x 2－3x ＋2＝0无实根，又二次函数y ＝2x 2－3x ＋2的图象开口向上，所以原不等式的解集为R .状元随笔 化二次项系数为正―→计算相应方程的判别式Δ及两根x 1，x 2――→函数图象结果题型二 三个“二次”之间的关系[经典例题]例2 已知关于x 的不等式ax 2＋bx ＋c >0的解集为{x |2<x <3}，求关于x 的不等式cx 2＋bx ＋a <0的解集．【解析】 方法一 由不等式ax 2＋bx ＋c >0的解集为{x |2<x <3}可知，a <0，且2和3是方程ax 2＋bx ＋c ＝0的两根，由根与系数的关系可知b a ＝－5，c a ＝6.由a <0知c <0，b c ＝－56，故不等式cx 2＋bx ＋a <0，即x 2＋b c x ＋a c >0，即x 2－56x ＋16>0，解得x <13或x >12，所以不等式cx2＋bx ＋a <0的解集为⎝ ⎛⎭⎪⎫－∞，13∪⎝ ⎛⎭⎪⎫12，＋∞. 方法二 由不等式ax 2＋bx ＋c >0的解集为{x |2<x <3}可知，a <0，且2和3是方程ax2＋bx ＋c ＝0的两根，所以ax 2＋bx ＋c ＝a (x －2)(x －3)＝ax 2－5ax ＋6a ⇒b ＝－5a ，c ＝6a ，故不等式cx 2＋bx ＋a <0，即6ax 2－5ax ＋a <0⇒6a ⎝ ⎛⎭⎪⎫x －13⎝ ⎛⎭⎪⎫x －12<0，故原不等式的解集为⎝ ⎛⎭⎪⎫－∞，13∪⎝ ⎛⎭⎪⎫12，＋∞. 状元随笔 由给定不等式的解集形式→确定a<0及关于a ，b ，c 的方程组→ 用a 表示b ，c →代入所求不等式→求解cx 2＋bx ＋a<0的解集方法归纳一元二次不等式与其对应的函数与方程之间存在着密切的联系，在解决具体的数学问题时，要注意三者之间的相互联系，并在一定条件下相互转换．(1)若一元二次不等式的解集为区间的形式，则区间的端点值恰是对应一元二次方程的根，要注意解集的形式与二次项系数的联系．(2)若一元二次不等式的解集为R 或∅，则问题可转化为恒成立问题，此时可以根据二次函数图象与x 轴的交点情况确定判别式的符号，进而求出参数的范围．跟踪训练2 已知一元二次不等式x 2＋px ＋q <0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12<x <13，求不等式qx 2＋px ＋1>0的解集．解析：因为x 2＋px ＋q <0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12<x <13，所以x 1＝－12与x 2＝13是方程x 2＋px ＋q ＝0的两个实数根，由根与系数的关系得⎩⎪⎨⎪⎧13－12＝－p ，13×⎝ ⎛⎭⎪⎫－12＝q ，解得⎩⎪⎨⎪⎧p ＝16，q ＝－16.所以不等式qx 2＋px ＋1>0即为－16x 2＋16x ＋1>0，整理得x 2－x －6<0，解得－2<x <3.即不等式qx 2＋px ＋1>0的解集为{x |－2<x <3}． 状元随笔观察给定不等式的解集形式→由根与系数的关系得p ，q 的方程组→确定p ，q 的值→求不等式qx 2＋px ＋1>0的解集题型三 含参数的一元二次不等式的解法[经典例题] 例3 解关于x 的不等式2x 2＋ax ＋2>0.【解析】 对于方程2x 2＋ax ＋2＝0，其判别式Δ＝a 2－16＝(a ＋4)(a －4)． ①当a >4或a <－4时，Δ>0，方程2x 2＋ax ＋2＝0的两根为x 1＝14(－a －a 2－16)，x 2＝14(－a ＋a 2－16)． ∴原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <14(－a －a 2－16)或x >14(－a ＋a 2－16).②当a＝4时，Δ＝0，方程有两个相等实根，x1＝x2＝－1，∴原不等式的解集为{x|x≠－1}．③当a＝－4时，Δ＝0，方程有两个相等实根，x1＝x2＝1，∴原不等式的解集为{x|x≠1}．④当－4<a<4时，Δ<0，方程无实根，∴原不等式的解集为R.状元随笔二次项系数为2，Δ＝a2－16不是一个完全平方式，故不能确定根的个数，因此需对判别式Δ的符号进行讨论，确定根的个数．方法归纳含参数一元二次不等式求解步骤(1)讨论二次项系数的符号，即相应二次函数图象的开口方向；(2)讨论判别式的符号，即相应二次函数图象与x轴交点的个数；(3)当Δ>0时，讨论相应一元二次方程两根的大小；(4)最后按照系数中的参数取值范围，写出一元二次不等式的解集．跟踪训练3 解关于x的不等式x2－(a＋a2)x＋a3>0.解析：原不等式可变形为(x－a)·(x－a2)>0，则方程(x－a)(x－a2)＝0的两个根为x1＝a，x2＝a2，(1)当a<0时，有a<a2，∴x<a或x>a2，此时原不等式的解集为{x|x<a或x>a2}；(2)当0<a<1时，有a>a2，即x<a2或x>a，此时原不等式的解集为{x|x<a2或x>a}；(3)当a>1时，有a2>a，即x<a或x>a2，此时原不等式的解集为{x|x<a或x>a2}；(4)当a＝0时，有x≠0；∴原不等式的解集为{x|x∈R且x≠0}；(5)当a＝1时，有x≠1，此时原不等式的解集为{x|x∈R且x≠1}；综上可知：当a<0或a>1时，原不等式的解集为{x|x<a或x>a2}；当0<a<1时，原不等式的解集为{x|x<a2或x>a}；当a＝0时，原不等式的解集为{x|x∈R且x≠0}；当a＝1时，原不等式的解集为{x|x∈R且x≠1}．状元随笔不等式左边分解因式→讨论a的范围→比较a与a 2的大小→写出不等式的解集题型四一元二次不等式的实际应用[经典例题]例4 某工厂的固定成本为3万元，该工厂每生产100台某产品的生产成本为1万元，设生产该产品x(百台)，其总成本为g(x)万元(总成本＝固定成本＋生产成本)，并且销售收入r (x )满足r (x )＝⎩⎪⎨⎪⎧－0.5x 2＋7x －10.5，0≤x ≤7，13.5，x ＞7.假定该产品产销平衡，根据上述统计规律求： (1)要使工厂有盈利，产品数量x 应控制在什么范围？ (2)工厂生产多少台产品时盈利最大？【解析】 (1)依题意得g (x )＝x ＋3，设利润函数为f (x )，则f (x )＝r (x )－g (x )，所以f (x )＝⎩⎪⎨⎪⎧－0.5x 2＋6x －13.5，0≤x ≤7，10.5－x ，x ＞7，要使工厂有盈利，则有f (x )>0，因为f (x )>0⇒⎩⎪⎨⎪⎧0≤x ≤7，－0.5x 2＋6x －13.5＞0或⎩⎪⎨⎪⎧x ＞7，10.5－x ＞0⇒⎩⎪⎨⎪⎧0≤x ≤7，x 2－12x ＋27＜0或⎩⎪⎨⎪⎧x ＞7，10.5－x ＞0⇒⎩⎪⎨⎪⎧0≤x ≤7，3＜x ＜9或⎩⎪⎨⎪⎧x >7，x <10.5.则3＜x ≤7或7＜x ＜10.5，即3＜x ＜10.5，所以要使工厂盈利，产品数量应控制在大于300台小于1 050台的范围内．(2)当3＜x ≤7时，f (x )＝－0.5(x －6)2＋4.5，故当x ＝6时，f (x )有最大值4.5，而当x ＞7时，f (x )＜10.5－7＝3.5，所以当工厂生产600台产品时盈利最大.(1)求利润函数f(x)⇒解不等式f(x)>0⇒回答实际问题． (2)根据第(1)题所求范围，分类讨论求函数最值⇒回答实际问题． 方法归纳解不等式应用题的四步骤(1)审：认真审题，把握问题中的关键量，找准不等关系． (2)设：引进数学符号，用不等式表示不等关系． (3)求：解不等式． (4)答：回答实际问题．特别提醒：确定答案时应注意变量具有的“实际含义”．跟踪训练4 某农贸公司按每担200元收购某农产品，并按每100元纳税10元(又称征税率为10个百分点)，计划可收购a 万担，政府为了鼓励收购公司多收购这种农产品，决定将征税率降低x (x ≠0)个百分点，预测收购量可增加2x 个百分点．(1)写出税收y (万元)与x 的函数关系式；(2)要使此项税收在税率调节后，不少于原计划税收的83.2%，试确定x 的取值范围．解析：(1)降低税率后的税率为(10－x )%，农产品的收购量为a (1＋2x %)万担，收购总金额为200a (1＋2x %)依题意得，y ＝200a (1＋2x %)(10－x )% ＝150a (100＋2x )(10－x )(0<x <10)． (2)原计划税收为200a ·10%＝20a (万元)． 依题意得，150a (100＋2x )(10－x )≥20a ×83.2%，化简得x 2＋40x －84≤0， ∴－42≤x ≤2.又∵0＜x ＜10，∴0＜x ≤2. ∴x 的取值范围是{x |0＜x ≤2}．状元随笔 根据题意，列出各数量之间的关系表，如下：原计划 降税后 价格(元/担)200 200税率 10% (10－x)%(0<x<10)收购量(万担) a a(1＋2x%) 收购总金额(万元) 200a 200·a(1＋2x%) 税收y(万元)200a·10%200·a(1＋2x%)(10－x)%一、选择题1．不等式3x 2－2x ＋1>0的解集为( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－1<x <13 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪13<x <1 C ．∅ D ．R解析：因为Δ＝(－2)2－4×3×1＝－8<0，所以抛物线y ＝3x 2－2x ＋1开口向上，与x 轴无交点，故3x 2－2x ＋1>0恒成立，即不等式3x 2－2x ＋1>0的解集为R .答案：D2．设m ＋n >0，则关于x 的不等式(m －x )(n ＋x )>0的解集是( )A ．{x |x <－n 或x >m }B ．{x |－n <x <m }C ．{x |x <－m 或x >n }D ．{x |－m <x <n }解析：不等式(m －x )(n ＋x )>0可化为(x －m )(x ＋n )<0，方程(x －m )(x ＋n )＝0的两根为x 1＝m ，x 2＝－n .由m ＋n >0，得m >－n ，则不等式(x －m )(x ＋n )<0的解集是{x |－n <x <m }，故选B.答案：B 3．不等式ax2＋5x ＋c >0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪13<x <12，则a ，c 的值分别为( ) A ．a ＝6，c ＝1 B ．a ＝－6，c ＝－1 C ．a ＝1，c ＝1 D ．a ＝－1，c ＝－6解析：由题意知，方程ax 2＋5x ＋c ＝0的两根为x 1＝13，x 2＝12，由根与系数的关系得x 1＋x 2＝13＋12＝－5a ，x 1·x 2＝13×12＝ca.解得a ＝－6，c ＝－1.答案：B4．若不等式x 2＋mx ＋m2>0的解集为R ，则实数m 的取值范围是( )A ．(2，＋∞)B ．(－∞，2)C ．(－∞，0)∪(2，＋∞) D．(0,2)解析：由题意知原不等式对应方程的Δ<0，即m 2－4×1×m2<0，即m 2－2m <0，解得0<m <2，故答案为D.答案：D 二、填空题5．不等式(2x －5)(x ＋3)<0的解集为________．解析：方程(2x －5)(x ＋3)＝0的两根为x 1＝52，x 2＝－3，函数y ＝(2x －5)(x ＋3)的图象与x 轴的交点坐标为(－3,0)和⎝ ⎛⎭⎪⎫52，0，所以不等式(2x －5)(x ＋3)<0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－3<x <52. 答案：⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－3<x <52 6．不等式2x －12x ＋1<0的解集为________．解析：原不等式可以化为(2x －1)(2x ＋1)<0，即⎝ ⎛⎭⎪⎫x －12⎣⎢⎡⎦⎥⎤x －⎝ ⎛⎭⎪⎫－12<0， 故原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ －12<x <12. 答案：⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ －12<x <12 7．用一根长为100 m 的绳子能围成一个面积大于600 m 2的矩形吗？若“能”，当长＝________ m ，宽＝________ m 时，所围成的矩形的面积最大．解析：设矩形一边的长为x m ，则另一边的长为(50－x )m,0<x <50.由题意，得x (50－x )>600，即x 2－50x ＋600<0，解得20<x <30.所以，当矩形一边的长在(20,30)的范围内取值时，能围成一个面积大于600 m 2的矩形．用S 表示矩形的面积，则S ＝x (50－x )＝－(x －25)2＋625(0<x <50)．当x ＝25时，S 取得最大值，此时50－x ＝25.即当矩形的长、宽都为25 m 时，所围成的矩形的面积最大．答案：25 25三、解答题8．解下列不等式：(1)x 2＋2x －15>0；(2)x 2－3x ＋5>0；(3)4(2x 2－2x ＋1)>x (4－x )．解析：(1)x 2＋2x －15>0⇔(x ＋5)(x －3)>0⇔x <－5或x >3，所以不等式的解集是{x |x <－5或x >3}．(2)因为Δ＝(－3)2－4×1×5＝－11<0，再根据函数y ＝x 2－3x ＋5图象的开口方向，所以原不等式的解集为R .(3)由原不等式得8x 2－8x ＋4>4x －x 2.∴原不等式等价于9x 2－12x ＋4>0.解方程9x 2－12x ＋4＝0，得x 1＝x 2＝23. 结合二次函数y ＝9x 2－12x ＋4的图象知，原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x ≠23. 9．若关于x 的一元二次不等式ax2＋bx ＋c <0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x <13或x >12，求关于x 的不等式cx 2－bx ＋a >0的解集．解析：由题意知⎩⎪⎨⎪⎧a <0，13＋12＝－b a ，13×12＝c a ，所以⎩⎪⎨⎪⎧ a <0，b ＝－56a >0，c ＝16a <0， 代入不等式cx 2－bx ＋a >0中得16ax 2＋56ax ＋a >0(a <0)． 即16x 2＋56x ＋1<0，化简得x 2＋5x ＋6<0， 所以所求不等式的解集为{x |－3<x <－2}． [尖子生题库] 10．解关于x 的不等式x 2－ax －2a 2<0.解析：方程x 2－ax －2a 2＝0的判断式Δ＝a 2＋8a 2＝9a 2≥0，得方程两根x 1＝2a ，x 2＝－a .(1)若a >0，则－a <x <2a ，此时不等式的解集为{x |－a <x <2a }；(2)若a <0，则2a <x <－a ，此时不等式的解集为{x |2a <x <－a }；(3)若a ＝0，则原不等式即为x 2<0，此时解集为∅. 综上所述，原不等式的解集为：当a >0时，{x |－a <x <2a }；当a <0时，{x |2a <x <－a }；当a ＝0时，∅.。

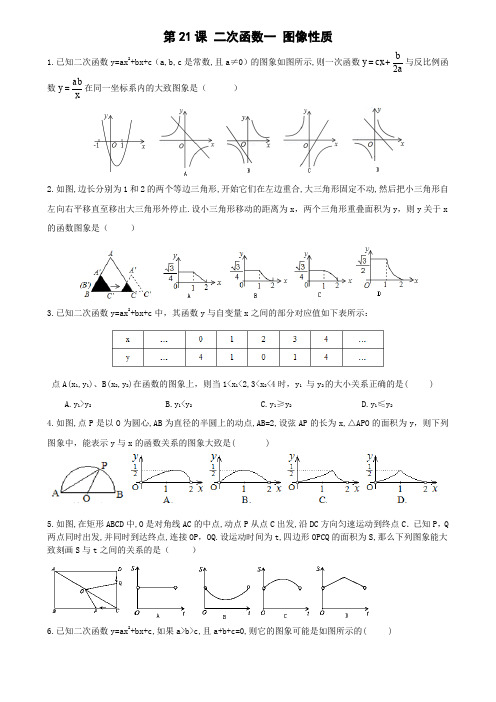
第21课 二次函数一 图像性质1.已知二次函数y=ax 2+bx+c （a,b,c 是常数,且a ≠0）的图象如图所示,则一次函数abcx y 2+=与反比例函数xaby =在同一坐标系内的大致图象是（ ）2.如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x ，两个三角形重叠面积为y ，则y 关于x 的函数图象是（ ）3.已知二次函数y=ax 2+bx+c 中，其函数y 与自变量x 之间的部分对应值如下表所示：点A(x 1,y 1)、B(x 2,y 2)在函数的图象上，则当1<x 1<2,3<x 2<4时，y 1 与y 2的大小关系正确的是( ) A.y 1>y 2 B.y 1<y 2 C.y 1≥y 2 D.y 1≤y 24.如图,点P 是以O 为圆心,AB 为直径的半圆上的动点,AB=2,设弦AP 的长为x,△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是( )5.如图,在矩形ABCD 中,O 是对角线AC 的中点,动点P 从点C 出发,沿DC 方向匀速运动到终点C ．已知P ，Q 两点同时出发,并同时到达终点,连接OP ，OQ.设运动时间为t,四边形OPCQ 的面积为S,那么下列图象能大致刻画S 与t 之间的关系的是（ ）6.已知二次函数y=ax 2+bx+c,如果a>b>c,且a+b+c=0,则它的图象可能是如图所示的( )7.关于函数y=2x 2-8x,下列叙述中错误的是( )A.函数图象经过原点B.函数图象的最低点是(2,-8)C.函数图象与x 轴的交点为(0,0),(4,0)D.函数图象的对称轴是直线x=-28.二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，下列结论正确的是（ ） A.a ＜0 B.b 2﹣4ac ＜0C.当﹣1＜x ＜3时,y ＞0D.12-=ab第8题图 第9题图 第10题图9.已知二次函数y=ax 2+bx+c （a,b,c 为常数，a ≠0）图象如图所示,有下列结论:①abc ＞0;②b 2-4ac ＜0;③a-b+c ＞0;④4a-2b+c ＜0，其中正确结论的个数是（ ）A.1B.2C.3D.4 10.已知二次函数y=ax 2+bx+c 的图象如图,其对称轴x=-1,给出下列结果:①b 2＞4ac;②abc ＞0; ③2a+b=0；④a+b+c ＞0；⑤a-b+c ＜0，则正确的结论是（ ）A.①②③④B.②④⑤C.②③④D.①④⑤11.已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示,现有下列结论:①b 2﹣4ac ＞0;②a ＞0;③b ＞0; ④c ＞0;⑤9a+3b+c ＜0，则其中结论正确的个数是（ ）A.2个B.3个C.4个D.5个第11题图 第12题图12.已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，在下列五个结论中：①2a-b ＜0；②abc ＜0； ③a+b+c ＜0；④a ﹣b+c ＞0；⑤4a+2b+c ＞0，错误的个数有（ ） A.1个 B.2个 C.3个 D.4个 13.已知抛物线y=5x 2+(m-1)x+m 与x 轴的两个交点在y 轴同侧,它们的距离平方等于4925,则m 的值为 ( ) A.-2 B.12 C.24 D.48 14.抛物线y=ax 2+2ax 的所有信息中，你能确定的是_____________________ 15.抛物线y=-3x 2+2x-1的图象与x 轴、y 轴交点个数是______个交点。

21.2 二次函数的图象和性质1.二次函数y=ax 2的图象和性质【知识与技能】1.能够利用描点法作出y=x 2的图象，并能根据图象认识和理解二次函数y=x2的性质.2.能作出二次函数y=-x 2的图象，并能够比较与y=x 2的图象的异同，初步建立二次函数表达式与图象之间的联系.【过程与方法】经历画二次函数y=x2的图象和探索性质的过程，获得利用图象研究函数性质的经验.【情感态度】培养学生数形结合的思想，积累数学经验，为后续学习服务.【教学重点】会画y=ax 2的图象，理解其性质.【教学难点】结合图象理解抛物线开口方向、对称轴、顶点坐标及基本性质，并归纳总结出来.一、情景导入，初步认知一次函数y=kx+b 和反比例函数x k y（k ≠0）图象是什么形状？有哪些性质呢？那么二次函数y=ax 2+bx+c （a ≠0）的图象会是什么样？通常怎样画一个函数的图象呢？——引入课题【教学说明】通过创设问题情景，引导学生复习描点法，复习借助图象分析性质的过程中注意分类讨论、由特殊到一般的解决问题的方法，为学习二次函数的图象奠定基础.二、思考探究，获取新知1.试着画出y=x 2的图象.【教学说明】让学生自己经历画y=x2的图象的过程，进一步了解用描点法的方法画图象的基本步骤，为将来画其他函数的图象奠定基础，同时也培养了学生动手操作能力，经历了知识的形成过程.2.观察二次函数y=x 2的图象，回答下列问题.（1）图象是轴对称图形吗？如果是，它的对称轴是什么？（2）图象有最低点吗？如果有，最低点的坐标是什么？（3）当x ＜0时，随着x 的增大，函数y 如何变化？当x ＞0时呢？【归纳结论】二次函数y=ax 2的图象是一条关于y 轴对称，过坐标原点并向上伸展的曲线，像这样的曲线叫做抛物线.抛物线与它的对称轴的交点叫做抛物线的顶点.3.在同一平面直角坐标系中，画出函数y=21x 2和y=2x 2的图象. 解：（1）列表.（2）描点、连线.4.探究.（1）观察二次函数y=21x 2和y=2x 2的图象，分别指出它们的开口方向、对称轴和顶点坐标；再指出图象有最高点还是有最低点？图象何时上升、何时下降？ （2）你能根据函数y=21x 2和y=2x 2的图象的共同特点，总结出二次函数y=ax 2(a ＞0)的性质吗？ 【归纳结论】二次函数y=ax 2(a ＞0)的图象及性质为：5.在同一平面直角坐标系中，画出函数y=-x 2、y=-21x 2和y=-2x 2的图象.仿照上面的表格，总结出y=ax 2(a ＜0)的性质.6.对比函数y=x 2和y=-x 2、y=21x 2和y=-21x 2、y=2x 2和y=-2x 2的图象，指出它们的相同与不同之处.7.思考：（1）a ＞0与a ＜0时，函数y=ax 2的图象有什么不同？（2）|a|的大小对函数y=ax 2的图象的开口大小有什么影响？（3）二次函数的图象是什么形状？【归纳结论】1.抛物线y=ax 2(a ≠0)的对称轴是y 轴，顶点是原点；2.a ＞0时，抛物线y=ax 2的开口向上，顶点是抛物线的最低点，a 越大，抛物线的开口越小；3.a ＜0时，抛物线y=ax 2的开口向下.顶点是抛物线的最高点，a 越大，抛物线的开口越大.【教学说明】让学生自己去观察分析，过程让学生自己去感受，结论让学生自己去总结，实现学生主动参与、探究新知的目的.三、运用新知，深化理解1.已知函数y=(m-2)x m2-7是二次函数，且开口向下，则m= -3 .【分析】它是二次函数，所以m 2-7=2,得m=±3,且开口向下，所以m-2＜0,得m ＜2.即：m=-3.2.已知抛物线y=ax 2经过点A （-2，-8）.（1）求此抛物线的函数解析式；（2）判断点B （-1，-4）是否在此抛物线上.【分析】（1）把a 的值求出即可；（2）把B 的坐标代入，等式成立则是在此抛物线上，否则不在.解：（1）把（-2，-8）代入y=ax 2中得：a=-2.∴解析式为：y=-2x 2（2）把（-1，-4）代入y=-2x 2中等式不成立，∴点B （-1，-4）不在此抛物线上.3.已知y=(k+2)42-+k k x 是二次函数，且当x ＞0时，y 随x 的增大而增大.（1）求k 的值；（2）求顶点坐标和对称轴.解：（1）由题意，得解得k=2.（2）二次函数为y=4x 2，则顶点坐标为（0，0），对称轴为y 轴.4.已知正方形周长为Ccm ，面积为Scm 2.（1）求S 和C 之间的函数关系式，并画出图象；（2）根据图象，求出S=1cm 2时，正方形的周长；（3）根据图象，求出C 取何值时，S ≥4cm 2.【分析】此题是二次函数实际应用问题，解这类问题时要注意自变量的取值范围；画图象时，自变量C 的取值应在取值范围内.解：（1）由题意，得S=161C 2(C ＞0). 列表：描点、连线，图象如图：（2）根据图象得S=1cm2时，正方形的周长是4cm.（3）根据图象得，当C≥8cm时，S≥4cm2.【教学说明】学生独立完成以后，让他们发表自己的看法，教师更正、强调.四、师生互动、课堂小结先小组内交流收获和感想而后以小组为单位派代表进行总结.教师作以补充.布置作业:教材“习题21.2”中第1、2题.本节课的教学过程的设计符合新课程标准和课程改革的要求，通过教学情景创设和优化课堂教学设计，体现了在活动中学习数学，在活动中“做数学”，并利用教具使教学内容形象、直观并具有亲和力，极大地调动了学生的学习积极性和热情，培养了学生学习数学的兴趣.教学过程始终坚持让学生自己去动脑、动手、动口，在分析、练习基础上掌握知识.整个教学过程都较好地落实了“学生的主体地位和教师的主导作用”，让学生体会到学习成功的乐趣.25.2用列举法求概率第1课时用列表法求概率【知识与技能】初步掌握直接列举法计算一些简单事件的概率的方法.【过程与方法】通过用列举法求简单事件的概率的学习，使学生在具体情境中分析事件.计算其发生的概率，解决实际问题.【情感态度】体会概率在生活实践中的应用，激发学习数学的兴趣，提高分析问题的能力.【教学重点】熟练掌握直接列举法计算简单事件的概率.正确理解和区分一次试验中包含两步或两个因素的试验.【教学难点】能不重不漏而又简洁地列出所有可能的结果.一、情境导入，初步认识1.复习回顾①概率的意义；②对于试验结果是有限等可能的事件的概率的求法.2.多媒体展示扫雷游戏，引入课题.二、典例精析，掌握新知我们在日常生活中，常常会用掷硬币的方式来决定游戏的胜负，下列请同学们思考下面的这种游戏规则是否公平.例老师向空中抛掷两枚同样的硬币，如果落地后一反一正，老师赢；如果落地后都只正面时，同学们赢，请问你们觉得这个游戏公平吗？【教学说明】对“游戏是否公平”实际是看两方出现的概率大小如何.所以解决本题的关键是，分别计算出“一正一反”与“都是正面”的概率各是多少并比较，这里教师要引导学生条理清楚地列举出所有可能的结果，学生思考交流.解：我们利用表格的形式，列举出所有可能的结果.∴这游戏不公平.问：“同时掷两枚硬币”与“先后掷一枚硬币”这两种试验的所有可能一样吗？答案：一样.三、运用新知，深化理解1.在“幸运52”栏目中，曾有一种竞猜游戏，游戏规则是：20个商标牌中，有5个商标牌背面注明了一定的奖金，其余商标牌的背面是一张“哭脸”，若翻到“哭脸”就不获奖，参与这个游戏的观众有三次翻牌的机会，且翻过的牌不能再翻，有一位观众已翻牌两次，一次获奖，一次不获奖，那么这位观众第三次翻牌获奖的概率是（）2.从甲、乙、丙三人中任意选两名代表参加会议，甲被选中的概率为（）3.在一个布袋里装有红、白、黑三种颜色的玻璃球各一个，它们除颜色外，没有其他区别，先从布袋中取出一个球，放回袋中并搅匀，再从袋中取一个球，则两次取出的恰好都是红球的概率是_____.4.袋子中装有红、绿各一个小球，除颜色外无其他差别，随机摸出1个小球后放回，再随机摸出一个.求下列事件的概率；（1）第一次摸到红球，第二次摸到绿球；（2）两次都摸到相同颜色的小球；（3）两次摸到的球中有一个绿球和一个红球.5.在“妙手推推推”的游戏中，主持人出示了一个9位数：258396417，让参与者猜商品价格，被猜的价格是一个4位数，也就是这个9位数中从左到右连在一起的某4个数字.如果参与者不知道商品的价格，从这些连在一起的所有4位数中，任意猜一个，求他猜中该商品的概率.【教学说明】本练习着重演练用列举法求简单事件的概率，可先让学生自主完成，再选派几名学生作答，教师再予以评点.【答案】1.B【解析】所有剩下的商标共20-2=18个，其中有奖的有5-1=4个，所以它第三次翻牌获奖的概率为4/18=2/9.2.C【解析】分析所有的可能结果为（甲、乙），（甲，丙），（乙，甲），（乙，丙），（丙，甲），（丙，乙）.事件A包含的结果为（甲、乙），（甲，丙）,（乙，甲），（丙，甲）共4个，故P（A）=4/6=2/3.3.1/9【解析】所有可能出现的结果有（红，红）、（红，白）、（红，黑）、（白，红）、（白，白）、（白，黑）、（黑，红）、（黑，白）、（黑，黑）共有9种，所以P（都是红球）=1/9.4.（1）1/4（2）1/2（3）1/25.所有可能结果有:2583,5839,8396,3964,9641,6417,其中只有一种是该商品的价格，所以猜中该商品的概率为1/6.四、师生互动，课堂小结1.本堂课你学到了什么知识，有哪些收获？2.你能不重不漏地列举出事件发生的所有可能吗？3.你能正确求出P（A）=m/n吗？【教学说明】围绕上述问题，教师引导学生交流归纳.用列举法求简单事件概率的一般步骤，重点是要让学生掌握方法.1.布置作业：从教材“习题25.2”中选取.2.完成练习册中本课时练习的“课后作业”部分.1.本节课通过以学生喜闻乐见的扫雷、掷硬币等游戏为载体，充分调动了学生的学习欲望，将学生摆在了真正的主体位置上，充分发挥了他们的主观能动性，从而让学生在趣味中掌握本节课的知识.生活中有许多有关概率的问题，本节课的学习亦能让学生尝试用概率的知识去解决生活中的问题，从而体会到概率知识在生活中的应用价值.2.本节课还通过普通列举法与列表法，对找出包含两个因素的试验结果的对比，让学生感受到列表法的作用与长处，使学生易于接受知识.3.教师引导学生交流归纳知识点，看学生能否会不重不漏地列举出事件发生的所有可能，能否找出事件A中包含几种可能的结果，并能求P（A），教学时要重点突出方法.二次函数说课稿（一）一、教材分析：1、教材所处的地位：二次函数是湘教版初中数学九年级（下册）的内容，在此之前，学生已经学过了函数及一次函数的内容，对于函数已经有了初步的认识。

第二章 一元二次函数、方程和不等式2.1 等式性质与不等式性质1．两个实数比较大小的方法(1)作差法⎩⎪⎨⎪⎧a －b >0⇔a > b a －b ＝0⇔a ＝ b a －b <0⇔a < b(a ，b ∈R )；(2)作商法⎩⎪⎨⎪⎧ab>1⇔a > b ab ＝1⇔a ＝ ba b<1⇔a < b (a ∈R ，b >0)．2.等式的性质性质1：如果a =b ，那么b =a ；性质2：如果a =b ，b =c ，那么b =c ； 性质3：如果a =b ，那么a ±c=b ±c ； 性质4：如果a =b ，那么a c=bc ； 性质5：如果a =b ，c 0≠那么cbc a =；3.不等式的性质性质1 a b >⇔ ________；(对称性) 性质2 a b >，b c >⇒ ________；(传递性)性质3 a b >⇒ ______________；(可加性) 推论：a b c >⇒＋___________；(移项法则) 性质4 a b >，0c >⇒ __________，(可乘性)a b >，0c ac bc <⇒<；(乘负反序性) 性质5 a b >，c d >⇒ ______________；(同向可加性) 性质6 0a b >>，0c d >>⇒ __________；(同正同向可乘性) 性质7 0a b >>⇒ __________()2n N n ∈≥，．(可乘方性)性质8 ①a >b ，ab >0⇒1a < 1b . ②a <0<b ⇒1a < 1b.（可倒性）典例例1 某矿山车队有4辆载重为10t 的甲型卡车和7辆载重为6t 的乙型卡车，且有9名驾驶员，此车队每天至少要运360t 矿石至冶炼厂．已知甲型卡车每辆每天可往返6次，乙型卡车每辆每天可往返8次，写出满足上述所有不等关系的不等式．例2 已知a ，b +例3 若0a b <<，则下列结论正确的是( )A ．22a b <B 2ab b < C ．11a b> D ．22ac bc > 例4 已知1025m <<，3015n -<<-，求m+n ，m n -与mn 的取值范围．例5 已知－1<x ＋y <4且2<x －y <3，则z ＝2x －3y 的取值范围是________．课时作业1.设a ,b ∈R ,若a -|b|>0,则下列不等式中正确的是( ) A.b -a>0 B.a 3+b 3<0 C.a 2-b 2<0 D.b+a>02、当1x ≤时，比较大小：33x 231x x -+．3、设1≤a －b ≤2, 2≤a ＋b ≤4，求4a －2b 的取值范围．4、已知a ∈R ,且a ≠1,比较a+2与31-a的大小.2.2 基本不等式1. 重要的不等式：a 2＋b 2≥2ab (a ，b ∈R )．2．基本不等式：ab ≤a ＋b2:两个正数的几何平均数不大于它们的算术平均数．（a+b ≥2ab ）注意：(1)此结论运用前提：一正、二定、三相等典例例1．（1）函数y ＝x ＋1x(x ＞0)的值域为( )A ．(－∞，－2]∪[2，＋∞)B ．(0，＋∞）C ．[2，＋∞)D ．(2，＋∞) （2）．已知m >0，n >0，且mn ＝81，则m ＋n 的最小值为( ) A ．18 B ．36 C ．81D ．243（3）.已知x ＜0，则y ＝2＋4x＋x 的最大值为_______例2、当x ＞0时，则y ＝2xx 2＋1的最大值为________．例3、若x >1，则x ＋4x －1的最小值为________．例4、已知a ＞0，b ＞0，且a ＋b ＝1，求1a ＋2b的最小值．例5、函数y ＝x 2＋2x －1(x >1)的最小值是( )A ．23＋2B ．23－2C ．2 3D ．2例6 如图所示动物园要围成相同面积的长方形虎笼四间，一面可利用原有的墙，其他各面用钢筋网围成．(1)现有可围36 m 长网的材料，每间虎笼的长、宽各设计为多少时，可使每间虎笼面积最大？ (2)要使每间虎笼面积为24 m2，则每间虎笼的长、宽各设计为多少时，可使围成四间虎笼的钢筋网总长最小？课时作业一、选择题1、已知x ＞0，函数y=x+的最小值是（ ） A ．2 B ．4C ．6D ．82、当x ∈R 时，x+的取值范围是（ ）A ．（﹣∞，﹣4]B ．（﹣∞，﹣4）∪（4，+∞）C ．[4，+∞）D ．（﹣∞，﹣4]∪[4，+∞）3、已知x ＞0，y ＞0，且2x+y=1，则xy 的最大值是( ) A ．B ．C ．4D ．84、的最小值为）（函数)0(2>+=ab abb a y A ．B．12C ．4D ．65、函数15(1)1y x x x =++>-的最小值为A ．5B ．6C 7 D.86、已知正数x,y 满足431x y +=，则x+3y 的最小值为A ．5B ．12C ．13D ．25 7、设，，若，则的最小值为 A ． B ．6 C ． D ．8、已知y=，其中x≥0，则y 的最小值为（ ）A ．1B ．C ．D ．9.某房地产开发公司计划在一楼区内建造一个长方形公园ABCD ,公园由形状为长方形A 1B 1C 1D 1的休闲区和环公园人行道(阴影部分)组成.已知休闲区A 1B 1C 1D 1的面积为4 000平方米,人行道的宽分别为4米和10米(如图所示).(1)若设休闲区的长和宽的比|A 1B 1||B 1C 1|=x (x>1),求公园ABCD所占面积S 关于x 的函数解析式;(2)要使公园所占面积最小,休闲区A 1B 1C 1D 1的长和宽该如何设计?1a >0b >2a b +=121a b+-3+2.3 二次函数与一元二次方程、不等式一、形如20(0) (0)ax bx c a ++><≠或其中的不等式称为关于x 的一元二次不等式． 二、“三个二次”之间的对应关系设()00022≠<++>++a c bx ax c bx ax 或相应的一元二次方程()002≠=++a c bx ax 的两根为1x ，2，则不等式的解的各种情况如下表：0>∆ 0=∆0<∆c bx ax y ++=2cbx ax y ++=2cbx ax y ++=2三、一元二次不等式的解法： （1）化二次项系数为正；（2）令左边=右边，求出两根x 1 , x 2; （当0<∆时，需另作考虑） （3）大于取两根之外，小于取两根之间。

二次函数与方程（组）或不等式知识讲
解
知识讲解
（1）最大值或最小值的求法
第一步确定a的符号：a&gt;0有最小值，a&lt;0有最大值；第二步求顶点，顶点的纵坐标即为对应的最大值或最小值。

（2）y轴与抛物线y=ax^2+bx+c的交点为（0，c）。

（3）与y轴平行的直线x=h与抛物线y=ax^2+bx+c有且只有一个交点（h，ah^2+bh+c）。

（4）抛物线与x轴的交点。

二次函数y=ax^2+bx+c的图像与x轴的两个交点的横坐标x1，x2是对应的一元二次方程ax^2+bx+c=0的两个实数根．抛物线与x轴的交点情况可以由对应的一元二次方程的根的判别式判定：
①有两个交点△&gt;0抛物线与x轴相交。

②有一个交点（顶点在x轴上）△=0抛物线与x轴相切；
③没有交点△&lt;0抛物线与x轴相离。

（5）平行于x轴的直线与抛物线的交点。

同（4）一样可能有0个交点，1个交点，2个交点．当
有2个交点时，两交点的纵坐标相等，设纵坐标为k，则横坐标是ax^2+bx+c=k的两个实数根。

（6）一次函数y=kx+n（k≠0）的图像L与二次函数y=ax^2+bx+c（a≠0）的图像G的交点，由方程组y=kx+n和y=ax^2+bx+c的解的数目确定：①当方程组有两组不同的解时L与G有两个交点；②方程组只有一组解时L与G只有一个交点；③方程组无解时L与G没有交点．
（7）利用函数图像求不等式的解集，先观察图像，找出抛物线与x轴的交点，&#8226;再根据交点坐标写出不等式的解集．注意：观察图像时不要看漏了其中的部分。

高中数学（必修一）二次函数与一元二次方程、不等式练习题（含答案解析）学校:___________姓名：___________班级：____________一、解答题1．（1）解不等式：245014x x -->+；（2）已知102α-<<，13β<<，求123αβ-的范围．2．当自变量x 在什么范围取值时,下列函数的值等于0?大于0?小于0?(1)2362y x x =-+;(2)225y x =-;(3)2610y x x =++;(4)231212y x x =-+-.3．已知{}{}2|430,||1|1A x x x B x x =-+≤=-≤ (1)求集合A 和B ；(2)求A ∪B ，A ∩B ，4．某地有一座水库，设计最大容量为128000m 3．根据预测，汛期时水库的进水量n S （单位：3m ）与天数()*n n N ∈的关系是10)n S n =.水库原有水量为800003m ，水闸泄水量每天40003m .当汛期来临第一天，水库就开始泄洪，估计汛期将持续10天，问：此期间堤坝会发生危险吗？请说明理由（水库水量超过最大容量，堤坝就会发生危险）.5．某小企业生产某种产品，月销售量x （件）与货价p （元/件）之间的关系为1602p x =-，生产x 件的成本50030r x =+元.该厂月产量多大时，月获利不少于1300元？6．解下列不等式：（1）24210x x +-< （2） 230x x -+≥（3）210x -> （4）26x x -+<-7．求函数y . 8．设全集为R ，{3A x x =≤或}9x ≥，{}29B x x =-<≤.(1)求A B ，A B ；(2)求()R B A .9．甲、乙两城相距100，在两城之间距甲城处的丙地建一核电站给甲、乙两城供电，为保证城市安全，核电站距两地的距离不少于10．已知各城供电费用（元）与供电距离（）的平方和供电量（亿千瓦时）之积都成正比，比例系数均是=0．25，若甲城供电量为20亿千瓦时/月，乙城供电量为10亿千瓦时/月，（1）把月供电总费用（元）表示成（）的函数，并求其定义域；（2）求核电站建在距甲城多远处，才能使月供电总费用最小．10．已知集合{}|2A x x =≥，{}|35B x x =<<.(1)求A B ；(2)定义{}|M N x x M x N -=∈∉且，求A B -.11．如图，为了测量两山顶M ，N 间的距离，飞机沿水平方向在A ，B 两点进行测量，A ，B ，M ，N 在同一个铅垂平面内.请设计一个测量方案，包括：(1)指出要测量的数据（用字母表示，并标示在图中）；(2)用文字和公式写出计算M ，N 间的距离的步骤.参考答案：1．（1）{}59x x <<；（2）112233αβ-<-<-．【分析】（1）通过一元二次不等式的解法计算即可；（2）通过不等式的性质计算即可.【详解】解：（1）214450x x --+>245014x x ∴+<- ()()590x x -∴<-{}59x x ∴<<（2）1032αβ-<<<<，111120133αβ∴-<<-<-<-， 112233αβ∴-<-<-2．(1)等于0,⎪⎪⎩⎭;大于0,|x x ⎧⎪<⎨⎪⎩或x >⎪⎭;小于0,|x x ⎧⎪<<⎨⎪⎪⎩⎭. (2)等于0,{5,5}-;大于0,{|55}x x -<<;小于0,{|5x x <-或5}x >.(3)等于0,∅;大于0,R ;小于0,∅.(4)等于0,{2};小于0,{|2}x x ≠;大于0,∅.【解析】根据二次函数与一元二次方程的关系,结合二次函数的图像与性质即可求解.【详解】（1）二次函数2362y x x =-+令23620x x -+=由一元二次方程的求根公式可知x =所以12x x ==结合二次函数的图像与性质可知,开口向上,与x 轴有两个交点,所以当x ∈⎪⎪⎩⎭时,函数值等于0;当|x x x ⎧⎪∈<⎨⎪⎩x >⎪⎭时,函数值大于0;当x x x ⎧⎪∈<<⎨⎪⎪⎩⎭时,函数值小于0.（2）二次函数225y x =-令2250x -=解一元二次方程可知5x =±所以125,5x x =-=结合二次函数的图像与性质可知:当{}5,5x ∈-时,函数值等于0;当{|5x x x ∈<-或}5x >时,函数值大于0;当{}|55x x x ∈-<<时,函数值小于0.（3）二次函数2610y x x =++则()231y x =++结合二次函数的图像与性质可知:当函数值等于0时x 为∅;当x ∈R 时,函数值大于0;当函数值小于0时x 为∅;（4）二次函数231212y x x =-+-则()232y x =--结合二次函数的图像与性质可知,开口向下,与x 轴有一个交点,所以:当{2}x ∈时函数值等于0; 当{}2x x x ∈≠时,函数值大于0;当函数值小于0时x 为∅;【点睛】本题考查了二次函数、一元二次方程和一元二次不等式的关系,二次函数图像与性质的应用,属于基础题.3．(1){}13A x x =≤≤；{}02B x x ≤≤ (2){}03A B x x ⋃=≤≤；{}12A B x x ⋂=≤≤【分析】（1）分别解两个不等式，即可得出答案；（2）根据交集和并集的运算即可得出答案.（1）解：解不等式2430x x -+≤得13x ≤≤，所以{}13A x x =≤≤，解不等式|1|1x -≤得02x ≤≤，所以{}02B x x ≤≤；（2） 解：{}03A B x x ⋃=≤≤，{}12A B x x ⋂=≤≤.4．第9天会有危险【分析】根据进水量与出水量，以及最多总增加水量列不等式，转化为一元二次不等式，解不等式求得第9天会有危险.【详解】设第n 天发生危险.由题意得400012800080000n >-，即2242560n n +->，得8n >.所以汛期的第9天会有危险.【点睛】注意对于数学应用性问题，首先要认真审题，理解题意；其次是建立合理的数学模型；最后用所学的数学知识去求解.同时，所得结果注意与事实相符，如本题n 是天数，需满足0n >.5．20~45【分析】根据销售额和成本以及获利要求列不等式，解一元二次不等式求得产量的取值范围.【详解】设月产量为x 件.由题意可知(1602)(50030)1300x x x -⨯-+≥，即2659000x x -+≤，得2045x ≤≤.【点睛】本小题主要考查函数的实际应用问题，考查一元二次不等式的解法，属于基础题.6．（1）{}73x x -<<；（2）{}03x x ≤≤；（3）{1x x <-或}1x >；（4）{2x x <-或}3x >.【分析】利用一元二次不等式的解法直接求解即可【详解】（1）由24210x x +-<，得(7)(3)0x x +-<，得73x -<<， 所以不等式的解集为{}73x x -<<，（2）由230x x -+≥，得230x x -≤，得03x ≤≤， 所以原不等式的解集为{}03x x ≤≤，（3）由210x ->，得(1)(1)0x x +->，解得1x <-或1x >， 所以不等式的解集为{1x x <-或}1x >，（4）由26x x -+<-，得260x x -->，(2)(3)0x x +->，解得2x <-或3x >， 所以原不等式的解集为{2x x <-或}3x >7．定义域为512x x ⎧⎫-≤<⎨⎬⎩⎭，用区间表示为51,2. 【分析】根据原函数列出不等式组求解即可.【详解】因为函数y 所以24506210x x x ⎧-++≥⎨-->⎩，解得1552x x -≤≤⎧⎪⎨<⎪⎩， 所以原函数定义域为512x x ⎧⎫-≤<⎨⎬⎩⎭，用区间表示为51,2. 8．(1){23A B x x ⋂=-<≤或}9x =，A B R =(2)(){2R B A x x ⋂=≤-或}9x >【分析】（1）根据集合的交集和并集的定义即可求解； （2）先根据补集的定义求出B R ，然后再由交集的定义即可求解. （1）解：因为{3A x x =≤或}9x ≥，{}29B x x =-<≤，所以{23A B x x ⋂=-<≤或}9x =，A B R =；（2）解：因为全集为R ，{3A x x =≤或}9x ≥，{}29B x x =-<≤，所以{2R B x x =≤-或}9x >，所以(){2R B A x x ⋂=≤-或}9x >.9．（1）（2）1003km 【详解】试题分析：（∪）甲城供电费用y 1=0．25×20x 2，乙城供电费用y 2=0．25×10（100-x ）2，总费用y=y 1+y 2，整理即可；因为核电站距甲城xkm ，则距乙城（100-x ）km ，由x≥10，且100-x≥10，得x 的范围；（∪）因为函数y=7．5x 2-500x+25000是二次函数，由二次函数的性质可得，x=-2b a时，函数y 取得最小值试题解析：（1）由题意知：经化简，为．定义域为[10,90]--- -5分（2）将（1）中函数配方为，所以当月供电总费用最小，为元．---10分．考点：函数模型的选择与应用；二次函数在闭区间上的最值10．(1){}|2x x ≥(2){}235x x x |≤≤≥或【分析】(1)直接根据集合并集的定义进行求解；(2)根据新定义{}|M N x x M x N -=∈∉且，即元素属于集合M 当不属于集合N ，从而可求出所求.（1）{}|2A x x =≥，{}|35B x x =<<，∴{}|2A B x x =≥；（2）{}|M N x x M x N -=∈∉且，{}|2A x x =≥，{}|35B x x =<<，∴{}235A B x x x -=|≤≤≥或.11．(1)答案见解析(2)答案见解析【分析】（1）需要测量的数据有A 到,M N 的的俯角11,αβ，B 到,M N 的的俯角22,αβ，AB 之间的距离d ，得到答案.（2）根据正弦定理得到()212sin sin d AM ααα=+，()221sin sin d AN βββ=-，再根据余弦定理得到答案. (1)需要测量的数据：A 到,M N 的的俯角11,αβ，B 到,M N 的的俯角22,αβ，AB 之间的距离d .(2)第一步：计算AM ABM 中，根据正弦定理：()122sin πsin d AM ααα=--，故()212sin sin d AM ααα=+. 第二步：计算AN ABN 中，根据正弦定理：()()212sin sin πd AN βββ=--，故()221sin sin d AN βββ=-. 第三步：计算MN AMN 中，根据余弦定理：()222112cos MN AM AN AM AN αβ=+-⋅-，即MN =。

中考热点01二次函数与方程、不等式，求参数范围一、解答题1(2023·浙江嘉兴·统考中考真题)在二次函数y=x2-2tx+3(t>0)中，(1)若它的图象过点(2,1)，则t的值为多少？(2)当0≤x≤3时，y的最小值为-2，求出t的值：(3)如果A(m-2,a),B(4,b),C(m,a)都在这个二次函数的图象上，且a<b<3，求m的取值范围．【答案】(1)t=3 2(2)t=5(3)3<m<4或m>6【分析】(1)将坐标代入解析式，求解待定参数值；(2)确定抛物线的对称轴，对待定参数分类讨论，若0<t≤3，当x=t时，函数值最小，求得t=5，若t>3，当x=3时，函数值最小，解得t=73(不合题意，舍去)；(3)由A(m-2,a),C(m,a)关于对称轴对称得m-1=t，且A在对称轴左侧，C在对称轴右侧；确定抛物线与y轴交点(0,3)，此交点关于对称轴的对称点为(2m-2,3)；由a<3,b<3且t>0∴4<2m-2解得m>3；分类讨论：当A，B都在对称轴左边时，4<m-2，解得m>6，当A，B分别在对称轴两侧时，4-(m-1)>m-1-(m-2)，解得m<4,∴3<m<4．【解析】(1)将(2,1)代入y=x2-2tx+3中，得1=4-4t+3，解得，t=3 2；(2)抛物线对称轴为x=t．若0<t≤3，当x=t时，函数值最小，∴t2-2t2+3=-2，解得t=±5．∵t>0，∴t=5若t>3，当x=3时，函数值最小，∴-2=9-6t+3，解得t=73(不合题意，舍去)综上所述t=5．(3)∵A(m-2,a),C(m,a)关于对称轴对称∴m-2+m2=t,m-1=t，且A在对称轴左侧，C在对称轴右侧∵抛物线与y轴交点为(0,3)，抛物线对称轴为直线x=t，∴此交点关于对称轴的对称点为(2m-2,3)∵a<3,b<3且t>0∴4<2m-2，解得m>3．当A，B都在对称轴左边时，∵a<b∴4<m-2，解得m>6，∴m>6当A，B分别在对称轴两侧时∵a<b∴B到对称轴的距离大于A到对称轴的距离∴4-(m-1)>m-1-(m-2)，解得m<4∴3<m<4综上所述3<m<4或m>6．【点睛】本题考查二次函数图象的性质、极值问题；存在待定参数的情况下，对可能情况作完备的分类讨论是解题的关键．2(2023·浙江·统考中考真题)已知点-m,0和3m,0在二次函数y=ax2+bx+3(a,b是常数，a≠0)的图像上．(1)当m=-1时，求a和b的值；(2)若二次函数的图像经过点A n,3且点A不在坐标轴上，当-2<m<-1时，求n的取值范围；(3)求证：b2+4a=0．【答案】(1)a=-1,b=-2(2)-4<n<-2(3)见解析【分析】(1)由m=-1可得图像过点1,0和-3,0，然后代入解析式解方程组即可解答；(2)先确定函数图像的对称轴为直线x=m，则抛物线过点n,3,0,3，即n=2m，然后再结合-2 <m<-1即可解答；(3)根据图像的对称性得-b2a =m，即b=-2am，顶点坐标为m,am2+bm+3；将点-m,0和3m,0分别代入表达式并进行运算可得am2=-1；则am2+bm+3=am2-2am2+3=-am2+3=4，进而得到12a-b24a=4，然后化简变形即可证明结论．【解析】(1)解：当m=-1时，图像过点1,0和-3,0，∴0=a+b+30=9a-3b+3，解得a=-1b=-2，∴y=-x2-2x+3，∴a=-1,b=-2．(2)解：∵函数图像过点-m,0和3m,0，∴函数图像的对称轴为直线x=m．∵图像过点n,3,0,3，∴根据图像的对称性得n=2m．∵-2<m<-1，∴-4<n<-2．(3)解：∵图像过点-m,0和3m,0，∴根据图像的对称性得-b2a=m．∴b=-2am，顶点坐标为m,am2+bm+3．将点-m,0和3m,0分别代人表达式可得0=am2-bm+3①0=9am2+3bm+3②①×3+②得12am2+12=0，∴am2=-1．∴am2+bm+3=am2-2am2+3=-am2+3=4．∴12a-b24a=4．∴12a-b2=16a．∴b2+4a=0．【点睛】本题主要考查了运用待定系数法求二次函数解析式、二次函数的对称性、解不等式等知识点，掌握二次函数的对称性是解答本题的关键．3(2023·浙江杭州·统考二模)在平面直角坐标系中，已知二次函数y=-x2+bx+c(b，c是常数)．(1)当b=2，c=3时，求该函数图象的顶点坐标．(2)设该二次函数图象的顶点坐标是(m,n)，当该函数图象经过点(1,-3)时，求n关于m的函数解析式．(3)已知b=2c+1，当0≤x≤2时，该函数有最大值8，求c的值．【答案】(1)1,4(2)n=m2-2m-2(3)2【分析】(1)将二次函数化为顶点式求解即可；(2)根据二次函数的性质和已知条件得到m=b2，n=c+b24，b=2m，c=-2-2m，进而求解即可；(3)当b=2c+1时，二次函数y=-x2+2c+1x+c的对称轴为直线x=2c+12=c+12，开口向下，分0≤c+12≤2 、c+12<0、c+12>2三种情况，利用二次函数的性质求解即可．【解析】(1)解：当b=2，c=3时，y=-x2+2x+3=-x-12+4，∴当b=2，c=3时，该函数图象的顶点坐标为1,4；(2)解：∵该函数图象经过点(1,-3)，∴-1+b+c=-3，则c=-2-b，∵该二次函数图象的顶点坐标是(m,n)，∴m=-b2×-1=b2，n=4×-1×c-b24×-1=4c+b24=c+b24，∴b=2m，c=-2-2m，∴n=-2-2m+4m24，即n=m2-2m-2；(3)解：当b=2c+1时，二次函数y=-x2+2c+1x+c的对称轴为直线x=2c+12=c+12，开口向下，∵0≤x≤2，∴当0≤c+12≤2即-12≤c≤32时，该函数的最大值为4×-1×c-2c+124×-1=c+2c+124=8，即4c2+8c-31=0，解得c1=-1+352，c2=-1-352，不合题意，舍去；当c+12<0即c<-12时，0≤x≤2时，y随x的增大而减小，∴当x=0时，y有最大值为c=8，不合题意，舍去；当c+12>2即c>32时，0≤x≤2时，y随x的增大而增大，∴当x=2时，y有最大值为-22+22c+1+c=8，解得c=2，符合题意，综上，满足条件的c的值为2．【点睛】本题考查二次函数的图象与性质，熟练掌握二次函数的图象与性质，利用分类讨论思想求解第(3)问是解答的关键．4(2023·浙江宁波·校考三模)如图，已知二次函数y=-x2+bx+c的图像经过点A4,1，点B0,5．(1)求该二次函数的表达式及顶点坐标；(2)点C m,n在该二次函数图像上，当m≤x≤4时，n的最大值为294，最小值为1，请根据图像直接写出m的取值范围．【答案】(1)该二次函数表达式y=-x2+3x+5；顶点坐标：32,294(2)-1≤m≤32【分析】(1)根据待定系数法即可求得；(2)把y=1代入抛物线解析式求得对应的x的值，再根据函数最大值和最小值，即可得答案．【解析】(1)解：∵二次函数y=-x2+bx+c的图像经过点A4,1，点B0,5，∴-16+4b+c=1c=5，解得b=3c=5，∴该二次函数为y=-x2+3x+5，∵y=-x-322+294，∴顶点为32,29 4；(2)让y=1，则-x2+3x+5=1，解得：x1=-1,x2=4，当x=32时，y=294，∵当m≤x≤4时，n的最大值为294，最小值为3 2，∴-1≤x≤32．【点睛】本题考查了待定系数法求二次函数的解析式，二次函数的性质，二次函数图像上点的坐标特征，数形结合是解题的关键．5(2023·浙江舟山·统考三模)在平面直角坐标系中，抛物线y=x2+bx+c(b，c是常数)经过点A1，0，点B0，3．点P在此抛物线上，其横坐标为m．(1)求此抛物线的解析式．(2)若-1≤x≤d时，-1≤y≤8，则d的取值范围是．(3)点P和点A之间(包括端点)的函数图象称为图象G，当图象G的最大值和最小值差是5时，求m的值．【答案】(1)y=x2-4x+3(2)2≤d≤5(3)m=2+5或m=2-6【分析】(1)利用待定系数法求出抛物线的解析式即可；(2)先求出抛物线的顶点坐标，得出函数的最小值为-1，把y=8代入y=x2-4x+3求出x1=5，x2= -1，根据-1≤x≤d时，-1≤y≤8，得出-1≤x≤d时，函数能够取到最小值，从而得出d的取值范围；(3)分情况讨论，当点P在顶点的右侧，即m≥2时，当点P在顶点与点A之间，即1<m<2时，当点P在点A的左侧，即m≤1时，分别求出m的值即可．【解析】(1)解：把点A1，0，点B0，3，代入抛物线y=x2+bx+c得：1+b+c=0c=3，解得：b=-4 c=3，∴抛物线的解析式为y=x2-4x+3；(2)解：∵y=x2-4x+3=x-22-1，∴抛物线的顶点坐标为2,-1，∴y的最小值为-1，把y=8代入y=x2-4x+3得8=x2-4x+3，解得：x1=5，x2=-1，∵-1≤x≤d时，-1≤y≤8，∴-1≤x≤d时，函数能够取到最小值，∴2≤d≤5；故答案为：2≤d≤5．(3)解：当点P在顶点的右侧，即m≥2时，此时函数能够取到最小值-1，∵图象G的最大值和最小值差是5，∴此时点P的纵坐标y P=-1+5=4，即点P的坐标为m,4，把m,4代入y=x2-4x+3得，m2-4m+3=4，解得：m=2+5或m=2-5(舍去)；当点P在顶点与点A之间时，即1<m<2，图象G的最大值和最小值差不可能是5；当点P在点A的左侧，即m≤1时，此时函数的最小值为0，∵图象G的最大值和最小值差是5，∴此时点P的纵坐标y P=0+5=5，即点P的坐标为m,5，把m,5代入y=x2-4x+3得，m2-4m+3=5，解得：m=2-6或m=2+6(舍去)；综上分析可知，m=2+5或m=2-6．【点睛】本题主要考查了二次函数的综合应用，求抛物线的解析式，抛物线的图象和性质，解题的关键是数形结合，注意进行分类讨论．6(2023·浙江杭州·统考二模)在平面直角坐标系中，设二次函数y=x2-2ax+1(a是常数)．(1)当a=2时，求函数图象的顶点坐标和对称轴．(2)若函数图象经过点(1，p)，(-1，q)，求证：pq≤4．(3)已知函数图象经过点A(-3，y1)，B(a+1，y2)，点C(m，y3)，若对于任意的4≤m≤6都满足y1>y3> y2，求a的取值范围．【答案】(1)顶点坐标(2，-3)，对称轴为直线x=2(2)见解析(3)3<a<3或a>72【分析】(1)当a=2时，y=x2-4x+1=x-22-3，进而可求顶点坐标与对称轴；(2)将(1，p)，(-1，q)，代入y=x2-2ax+1得，p=2-2a，q=2+2a，则pq=2-2a=42+2a-4a2≤4，进而结论得证；(3)由题意知，二次函数图象开口向上，对称轴为直线x =a ，则B (a +1，y 2)在对称轴右侧，由对于任意的4≤m ≤6都满足y 1>y 3>y 2，则点A ，B ，C 存在如下情况：情况1，如图1，根据二次函数的图象与性质，以及y 1>y 3>y 2，列不等式-3 2-2a ×-3 +1>62-2a ×6+1，a +1<4，求解集即可；情况2，如图2，由二次函数的图象与性质可得-3 2-2a ×-3 +1>42-2a ×4+1，6<a ；a +12-2a ×a +1 +1<62-2a ×6+1，分别求解满足要求的解集即可．【解析】(1)解：当a =2时，y =x 2-4x +1=x -2 2-3，∴顶点坐标(2，-3)，对称轴为直线x =2；(2)证明：将(1，p )，(-1，q )，代入y =x 2-2ax +1得，p =1-2a +1=2-2a ，q =1+2a +1=2+2a ，∴pq =2-2a 2+2a =4-4a 2≤4，∴pq ≤4；(3)解：由题意知，二次函数图象开口向上，对称轴为直线x =a ，则B (a +1，y 2)在对称轴右侧，∵对于任意的4≤m ≤6都满足y 1>y 3>y 2，∴点A ，B ，C 存在如下情况：情况1，如图1，由二次函数的图象与性质可得-3 2-2a ×-3 +1>62-2a ×6+1，解得a >32，a +1<4，解得a <3，∴32<a <3；情况2，如图2，由二次函数的图象与性质可得-3 2-2a ×-3 +1>42-2a ×4+1，解得a >12，又∵6<a ，a +1 2-2a ×a +1 +1<62-2a ×6+1，解得a <5或a >7，∴a >7；综上所述，a 的取值范围为32<a <3或a >7．【点睛】本题考查了二次函数的图象与性质．解题的关键在于数形结合．7(2023·浙江杭州·统考二模)已知函数y 1=x 2-m +2 x +2m +3,y 2=nx +k -2n (m ，n ，k 为常数且n ≠0)．(1)若y 1的图象经过点A -1,3 ，求该函数的表达式．(2)若函数y 1，y 2的图象始终经过同一定点M ．①求点M 的坐标和k 的值．②若m ≤2，当-1≤x ≤2时，总有y 1≤y 2，求m +n 的取值范围．【答案】(1)y 1=x 2-x +1(2)①M 2，3 ，k =3；②m +n ≤-1【分析】(1)利用待定系数法求解即可；(2)①先求出函数y 1经过定点2，3 ，则M 2，3 ，且M 2，3 在函数y 2的图象上，由此把M 2，3 代入y 2解析式中求出k 的值即可；②先求出抛物线y 1的对称轴在定点M 2，3 的左侧，再结合函数图象可知当x =-1时，一次函数的函数值要大于等于二次函数的函数值，由此建立不等式求解即可．【解析】(1)解：把A -1,3 代入y 1=x 2-m +2 x +2m +3中得：-1 2+m +2 +2m +3=3，解得m =-1，∴y 1=x 2--1+2 x -2+3=x 2-x +1；(2)解：①在y 1=x 2-m +2 x +2m +3中，当x =2时，y 1=22-2m +2 +2m +3=4-2m -4+2m +3=3，∴函数y 1经过定点2，3 ，∵函数y 1，y 2的图象始终经过同一定点M ，∴M 2，3 ，且M 2，3 在函数y 2的图象上，∴2n +k -2n =3，∴k =3；②∵m≤2，抛物线y1的对称轴为直线x=m+2 2，∴抛物线y1的对称轴在定点M2，3的左侧，由①得y2=nx+3-2n，∵m≤2，当-1≤x≤2时，总有y1≤y2，∴如图所示，当x=-1时，一次函数的函数值要大于等于二次函数的函数值∴-12+m+2+2m+3≤-n+3-2n∴3m+3n≤-3，∴m+n≤-1．【点睛】本题主要考查了求二次函数解析式，二次函数的性质，二次函数与不等式，解题的关键是理解题意，灵活运用所学知识解决问题．8(2023·浙江杭州·统考二模)已知二次函数y1=ax x-ma≠0和一次函数y2=ax+b a≠0．(1)二次函数y1的图象过1,0,2,2点，求二次函数的表达式；(2)若一次函数y2与二次函数y1的图象交于x轴上同一点，且这个点不是原点．①求证：b=-am；②若两个函数图象的另一个交点为二次函数的顶点，求m的值．【答案】(1)二次函数y1的表达式为y1=x x-1；(2)①证明见解析，②m=2【分析】(1)待定系数法，求出函数解析式即可．(2)①先求出二次函数y1=ax x-ma≠0与x轴的交点坐标，进而得到一次函数y2与二次函数y1的图象的交点坐标，代入一次函数，即可得出结论；②求出二次函数的顶点坐标，代入一次函数即可得出结果．【解析】(1)解：∵二次函数y1=ax x-ma≠0过1,0,2,2，∴m=1，∴二次函数的表达式为y1=ax x-1，将2,2点代入，得2=2a，∴a=1；∴二次函数y1的表达式为y1=x x-1．(2)①∵当y=0时，ax x-m=0解得：x1=0,x2=m，∴二次函数y1=ax x-1与x轴交于0,0和m,0点，又一次函数y2与二次函数y1的图象交于x轴上同一点，且这个点不是原点，∴一次函数y2过m,0点，∴am +b =0，∴b =-am ；②∵b =-am ，∴y 2=ax -am ，∵两个函数图象的另一个交点为二次函数的顶点，∵二次函数y 1=ax x -m 的顶点为m 2,-am 24，∴y 2=ax -am 过m 2,-am 24，∴-am 24=-am 2∵a ≠0,m ≠0，∴m 2=2m ，∴m =2．【点睛】本题考查二次函数与一次函数的综合应用．熟练掌握二次函数与一次函数的图象和性质，是解题的关键．9(2023·浙江杭州·杭州市公益中学校考二模)在平面直角坐标系中，当x =-2和x =4时，二次函数y =ax 2+bx -2(a ，b 是常数，a ≠0)的函数值相等．(1)若该函数的最大值为1，求函数的表达式，并写出函数图象的顶点坐标；(2)若该函数的图象与x 轴有且只有一个交点，求a ，b 的值．(3)记(2)中的抛物线为y 1，将抛物线y 1向上平移2个单位得到抛物线y 2，当-2≤x ≤m 时，抛物线y 2的最大值与最小值之差为8，求m 的值．【答案】(1)y =-3x -1 2+1，1，1 ；(2)a =-2，b =4；(3)1-5．【分析】(1)根据二次函数的性质及对称轴即可解答；(2)根据二次函数与x 轴的交点个数及二次函数的性质即可解答；(3)根据二次函数的平移规律及二次函数的性质即可解答．【解析】(1)解：∵当x =-2和x =4时，二次函数y =ax 2+bx -2(a ，b 是常数，a ≠0)的函数值相等，∴二次函数的对称轴为x =-2+42=1，4a -2b -2=16a +4b -2①，∵该函数的最大值为1，∴该函数的顶点坐标为1，1 ，∴1=a +b -2②，∴由①②可得：a =-3b =6 ，∴函数表达式为：y =-3x -1 2+1；(2)解：∵该函数的图象与x 轴有且只有一个交点，∴一元二次方程ax 2+bx -2=0，该函数的顶点坐标为1，0 ，∴Δ=b 2+8a =0①，a +b -2=0①，∴由①②可得a =0b =2(舍去)，a =-2b =4 ，∴a =-2，b =4；(3)解：由(2)可得y 1的解析式为：y 1=-2x 2+4x -2，∵将抛物线y 1向上平移2个单位得到抛物线y 2，∴y 2=-2x 2+4x ，∴当x =-2时，y 2=-16，∵y 2的顶点坐标为1，2 ，且当-2≤x ≤m 时，抛物线y 2的最大值与最小值之差为8，∴m <1，y 2随x 的增大而增大，∴-16+8=-8，∴-2m 2+4m =-8，∴m -1 2=5，∴m =1±5，∵m <1，∴m =1-5．【点睛】本题考查了二次函数的性质，二次函数的顶点坐标，二次函数的最值，二次函数与x 轴的交点坐标，掌握二次函数的性质是解题的关键．10(2023·浙江丽水·统考二模)二次函数y =x 2+bx +c 的图象与x 轴交于点A x 1,0 ,B x 2,0 且x 1≠x 2．(1)当x 1=2，且b +c =-6时，①求b ，c 的值②当t ≤x ≤t +2时，二次函数y =x 2+bx +c 的最小值为2t ，求t 的值；(2)若x 1=3x 2，求证：32b -c ≤3．【答案】(1)①b =2，c =-8；②t =4或t =22(2)见解析【分析】(1)①依题意，b +c =-64+2b +c =0 ，解方程组即可求解；②根据①得出解析式，对称轴为直线x =-1，进而分t +2≤-1，t <-1<t +2，t ≥-1，三种情况求得最小值，根据题意建立方程，解方程即可求解；(2)由题意得：x 12+bx 1+c =0，x 22+bx 2+c =0，将x 1=3x 2代入，得出 9x 22+3bx 2+c =0，得出x 2=-14b ，代入x 22+bx 2+c =0得c =316b 2，进而32b -c =-316b -4 2+3≤3，即可得证．【解析】(1)解：①依题意，b +c =-64+2b +c =0解得b =2，c =-8②y =x 2+2x -8=x +1 2-9若t +2≤-1，即t ≤-3，当x =t +2时，y =t +2+1 2-9=2t ，解得：t =0(舍去)或t =-4；若t <-1<t +2，即-3<t <-1，当x =-1时，y =-1+1 2-9=2t ，解得：t =-4.5(舍去)；若t ≥-1，当x =t 时，y =t +1 2-9=2t ，解得：t =-22(舍去)或t =22；综上所述：t =4或t =22．(2)∵x 1≠x 2，x 1=3x 2 ∴3x 2≠x 2 ∴x 2≠0由题意得：x 12+bx 1+c =0，x 22+bx 2+c =0，∴9x 22+3bx 2+c =0，∴8x 22+2bx 2=0∴2x 24x 2+b =0∵x 2≠0　∴4x 2+b =0　即x 2=-14b∴把x 2=-14b ，代入x 22+bx 2+c =0得c =316b 2；∴32b -c =32b -316b 2=-316b 2-8b =-316b -4 2+3≤3．【点睛】本题考查了二次函数的性质，熟练掌握函数的性质是解题的关键．11(2023·浙江杭州·统考二模)二次函数y =ax 2+bx -1(a ，b 为常数，a ≠0)的图像经过点A 1,2 ．(1)求该二次函数图像的对称轴(结果用含a 的代数式示)(2)若该函数图像经过点B 3,2 ；①求函数的表达式，并求该函数的最值．②设M x 1,y 1 ，N x 2,y 2 是该二次函数图像上两点，其中x 1，x 2是实数．若x 1-x 2=1，求证：y 1+y 2≤112【答案】(1)x =a -32a(2)①y =-x 2+4x -1，最大值为3；②见解析【分析】(1)首先将点A 1,2 代入表达式，然后利用对称轴公式求解即可；(2)①将点B 3,2 代入求出函数的表达式，然后转化成顶点式即可求出该函数的最值；②首先根据x 1-x 2=1得到x 1=x 2+1，然后表示出y 1+y 2利用二次函数的性质求解即可．【解析】(1)将点A 1,2 代入y =ax 2+bx -1得，a +b -1=2，∴b =3-a ，∴二次函数y =ax 2+3-a x -1，∴对称轴为x =-3-a 2a =a -32a；(2)①将B 3,2 代入y =ax 2+3-a x -1得，9a +9-3a -1=2，∴解得a =-1，∴二次函数y =-x 2+4x -1，∴y =-x 2+4x -1=-x 2-4x -1=-x -2 2+3，∵-1<0，∴抛物线开口向下，∴该函数的最大值为3；②∵x 1-x 2=1∴x 1=x 2+1，∴y 1+y 2=-x 12+4x 1-1-x 22+4x 2-1=-x 2+1 2+4x 2+1 -1-x 22+4x 2-1=-2x 22+6x 2+1=-2x 2-3 2+112∵-2<0，∴y 1+y 2的最大值为112，∴y 1+y 2≤112．【点睛】本题考查了根据对称性求对称轴，待定系数法求二次函数解析式，掌握二次函数图象的性质是解题的关键．12(2023·浙江杭州·统考一模)二次函数y =ax 2+bx +c (a ≠0)与x 轴交于A (1,0),B (m ,0)两点．(1)当a =1,b =2时，求m 的值．(2)当0<a <2,c =2时，①求证：m >1．②点C x 1,y 1 ,D x 2,y 2 在该抛物线上，且x 1>x 2,x 1+x 2<2，试比较y 1与y 2的大小．【答案】(1)-3；(2)①见解析；(2)y 1<y 2【分析】(1)当a =1,b =2时，y =x 2+2x +c ，把A (1,0)代入求得c =-3，得到y =x 2+2x -3，把B (m ,0)代入y =x 2+2x -3得，0=m 2+2m -3，解方程即可得到答案；(2)①把A (1,0),B (m ,0)代入y =ax 2+bx +c (a ≠0)得a +b +c =0，am 2+bm +c =0，由c =2得到a +b +2=0，am 2+bm +2=0进一步得am 2-a +2 m +2=0，则Δ=a +2 2-4a ×2=a -2 2≥0，由0<a <2,解方程求出m ，即可判断．②由①得b =-a -2，c =2，则y =ax 2-a +2 x +2，把C x 1,y 1 ,D x 2,y 2 代入得y 1=ax 12-a +2 x1+2，y 2=ax 22-a +2 x 2+2，则y 1-y 2=x 1-x 2 a x 1+x 2 -a +2 ，由x 1>x 2,x 1+x 2<2，得到x 1-x 2>0,,a x 1+x 2 -a +2 <0，进一步即可得到答案．【解析】(1)解：当a =1,b =2时，y =x 2+2x +c ，把A (1,0)代入得，0=1+2+c ，解得c =-3，∴y =x 2+2x -3，把B(m,0)代入y=x2+2x-3得，0=m2+2m-3，解得m=1或-3；∵二次函数y=ax2+bx+c(a≠0)与x轴交于A(1,0),B(m,0)两点，∴m=-3；(2)①把A(1,0),B(m,0)代入y=ax2+bx+c(a≠0)得，a+b+c=0，am2+bm+c=0，∵c=2，∴a+b+2=0，am2+bm+2=0，由b=-a-2得到am2-a+2m+2=0，则Δ=a+22-4a×2=a-22≥0，∴m=a+2±a-222a=a+2±a-22a，∴m1=1(舍去)，m2=2a，∵0<a<2,∴m>1．②由①得b=-a-2，c=2，∴y=ax2-a+2x+2，把C x1,y1,D x2,y2代入得，y1=ax12-a+2x1+2，y2=ax22-a+2x2+2，∴y1-y2=ax12-a+2x1+2-ax22-a+2x2+2=a x1-x2x1+x2-a+2x1-x2=x1-x2a x1+x2-a+2，∵x1>x2,x1+x2<2，∴x1-x2>0,a x1+x2-a+2<2a-a+2,∵0<a<2,∴2a-a+2=a-2<0，∴a x1+x2-a+2<0，∴y1-y2=x1-x2a x1+x2-a+2<0，∴y1<y2．【点睛】此题考查了二次函数的性质、解一元二次方程、比较函数值大小等知识，读懂题意并准确计算是解题的关键．13(2023·浙江绍兴·统考一模)在平面直角坐标系xOy中，已知抛物线y=x2-2tx+1．(1)求该抛物线的对称轴(用含t的式子表示)；(2)若点M t-2，m，N t+3，n在抛物线y=x2-2tx+1上，试比较m，n的大小；(3)P x1，y1，Q x2，y2是抛物线y=x2-2tx+1上的任意两点，若对于-1≤x1<3且x2=3，都有y1≤y2，求t的取值范围；(4)P t+1，y1，Q2t-4，y2是抛物线y=x2-2tx+1上的两点，且均满足y1≥y2，求t的最大值．【答案】(1)抛物线的对称轴为直线x=t；(2)n>m；(3)t≤1；(4)t的最大值为5．【分析】(1)把解析式化成顶点式即可求得；(2)根据二次函数的性质以及二次函数图象上点的坐标特征即可判断；(3)分3种情况求解即可；(4)分两种情况讨论，根据题意列出关于t的不等式，解不等式即可解决问题．【解析】(1)解：∵y=x2-2tx+1=x-t2-t2+1，∴抛物线的对称轴为直线x=t；(2)解：∵点M t-2，m在抛物线y=x2-2tx+1上，，N t+3，n∴抛物线的开口向上，对称轴为直线x=t，又∵|t-(t-2)|=2，|t-(t+3)|=3，2<3，∴点N t+3，n离抛物线y=x2-2tx+1的对称轴距离较大，∴n>m；(3)解：∵抛物线的开口向上，∴离抛物线y=x2-2tx+1的对称轴距离较大，函数值越大．当t>3时，点P离对称轴远，不符合题意；当-1≤t≤3时，由题意得，3-t≥t--1，解得t≤1，∴-1≤t≤1时，都有y1≤y2；当t<-1时，点Q离对称轴远，都有y1≤y2．综上，当t≤1时，都有y1≤y2．(4)解：∵抛物线的开口向上，对称轴为直线x=t，∴点P在抛物线y=x2-2tx+1对称轴的右侧，∵y1≥y2，①当点Q在对称轴的右侧或在对称轴上，且在点P的左侧或与点P重合时满足条件，∴2t-4≥t且2t-4≤t+1，解得4≤t≤5；②当点Q在对称轴的左侧，且点Q到抛物线对称轴的距离小于或等于点P到对称轴的距离时满足条件，∴2t-4<t，t-2t-4≤t+1-t，解得3≤t<4，综上所述：当3≤t≤5时，满足题意．∴t的最大值为5．【点睛】本题考查了二次函数图象与系数的关系，二次函数图象上点的坐标特征，二次函数的性质，掌握性质是解题的关键．14(2023·浙江杭州·模拟预测)在平面直角坐标系中，抛物线y=x2-2mx+m2+1存在两点A m-1,y1．，B m+2,y2(1)求抛物线的对称轴；(用含m的式子表示)(2)记抛物线在A，B之间的部分为图象F(包括A，B两点)，y轴上一动点C0,a，过点C作垂直于y轴的直线l与F有且仅有一个交点，求a的取值范围；(3)若点M2,y3也是抛物线上的点，记抛物线在A，M之间的部分为图象G(包括M，A两点)，记图形G 上任意一点的纵坐标的最大值与最小值的差为t，若t≥y2-y1，求m的取值范围．【答案】(1)x=m(2)a=1或2<a≤5(3)m≤2-3或m≥4【分析】(1)将一般式转化为顶点式即可得解；(2)将A m-1,y1代入解析式，求出y1,y2，画出函数图象，利用数形结合的方法求解即 ，B m+2,y2可；(3)分点M在点A的左侧；点A的右侧，对称轴的左侧；以及对称轴的右侧，结合图象进行分类讨论求解即可．【解析】(1)解：y=x2-2mx+m2+1=x-m2+1，∴对称轴为：x=m；(2)解：由y=x2-2mx+m2+1=x-m2+1可知：抛物线的顶点坐标为：m,1，当x=m-1时：y1=m-1-m2+1=2，当x=m+2时：y1=m+2-m2+1=5，∴A m-1,2,B m+2,5，∵C0,a，∴过点C垂直于y轴的直线l：y=a，如图：由图象可知：当a=1或2<a≤5时，直线l与F有且仅有一个交点，∴a的取值范围为：a=1或2<a≤5；(3)解：∵A m-1,2，,B m+2,5∴t≥y2-y1=5-2=3，当x=2时，y3=m2-4m+5，∴M2,m2-4m+5①当M在点A的左侧，即：m-1>2，m>3时：在对称轴的左侧，y随x的增大而减小，∴M点的纵坐标最大，A点的纵坐标最小，∴t=m2-4m+5-2=m2-4m+3≥3，解得：m≥4或m≤0(舍掉)；②当M在点A的右侧，对称轴的左侧时，此时t<2-1=1，不符合题意；③当M对称轴的右侧，即m<2时，当y3≤2时，此时A点的纵坐标最大，抛物线的顶点处的纵坐标最小：t=2-1=1<3不符合题意；③当M对称轴的右侧，即m<2时，当y3>2时，此时M 点的纵坐标最大，抛物线的顶点处的纵坐标最小，∴t =m 2-4m +5-1=m 2-4m +4≥3，解得：m ≥2+3(舍)，或m ≤2-3；∴m ≤2-3；综上：m ≤2-3或m ≥4．【点睛】本题考查二次函数的综合应用．熟练掌握二次函数的图象和性质，利用数形结合的思想进行求解是解题的关键．二、填空题(共0分15(2022春·九年级课时练习)抛物线y =(k -1)x 2-x +1与x 轴有交点，则k 的取值范围是．【答案】k ≤54且k ≠1【分析】直接利用根的判别式进行计算，再结合k -1≠0，即可得到答案．【解析】解：∵抛物线y =(k -1)x 2-x +1与x 轴有交点，∴Δ=(-1)2-4×(k -1)×1≥0，∴k ≤54，又∵k -1≠0，∴k ≠1，∴k 的取值范围是k ≤54且k ≠1；故答案为：k ≤54且k ≠1．【点睛】本题考查了二次函数与坐标轴有交点的问题，解题的关键是掌握根的判别式求参数的取值范围．16(2020秋·九年级课时练习)抛物线y =x 2+8x -4与直线x =-4的交点坐标是．【答案】(-4，-20)【解析】解：∵当x =-4时，y =(-4)2+8×(-4)-4=-20，∴抛物线y =x 2+8x -4与直线x =-4的交点坐标是(-4，-20)．故答案为(-4，-20)．17(2023·安徽淮北·校考一模)若对称轴为直线x =-2的抛物线y =ax 2+bx +c (a ≠0)经过点(1,0)，则一元二次方程ax 2+bx +c =0的根是．【答案】x 1=-5，x 2=1【分析】根据二次函数的对称性求出(1,0)的对称点，即可得到答案；【解析】解：∵对称轴为直线x =-2的抛物线y =ax 2+bx +c (a ≠0)经过点(1,0)，∴点(1,0)的对称点是：(-2×2-1,0)，即(-5,0)，∴方程ax 2+bx +c =0的根是x 1=-5，x 2=1，故答案为：x 1=-5，x 2=1；【点睛】本题考查抛物线的性质及二次函数与一元二次方程关系，解题的关键是根据对称性求出对称点．18(2021春·九年级课时练习)抛物线y =2x 2+2k -1 x -k (k 为常数)与坐标轴交点的个数是．【答案】3个【分析】先令y =0，得出关于x 的一元二次方程，由△>0得方程有两个不相等的实数根，即抛物线与x 轴有两个不同的交点，与y 轴有一个交点．【解析】解：∵抛物线y =2x 2+2(k -1)x -k (k 为常数)，∴当y =0时，0=2x 2+2(k -1)x -k ，∴△=[2(k -1)]2-4×2×(-k )=4k 2+4>0，∴0=2x 2+2(k -1)x -k 有两个不相等的实数根，∴抛物线y =2x 2+2(k -1)x -k (k 为常数)与x 轴有两个交点，∴抛物线y =2x 2+2(k -1)x -k (k 为常数)与y 轴有一个交点，所以，抛物线y =2x 2+2k -1 x -k (k 为常数)与坐标轴交点有3个，故答案为：3个．【点睛】本题考查抛物线与x 、y 轴的交点，解答本题的关键是明确题意，利用二次函数的性质解答．19(2023·湖北武汉·统考模拟预测)已知二次函数y =ax 2+bx +c a ≠0 的部分图象如图所示，图象过点-1,0 ，对称轴为直线x =1，下列结论：①2a +b =0；②当m ≠-1时，am 2-b m +1 <a ；③若点A -2,y 1 ，点B 12,y 2 ，点C 52,y 3 均在该图象上，则y 1<y 3<y 2；④若关于x 的方程a x +1 x -3 =p p >0 的两根都是整数，则这样的p 值有3个．其中正确的结论有(填序号)．【答案】①②③【分析】根据图象对称轴为直线x =1，可得2a =-b ；可判断①；设w =am 2-b m +1 ，可得w =am 2-b m +1 =am 2+2a m +1 =a m +1 2+a ，再由a <0，可得当m =-1时，w 取得最大值，最大值为a ，可判断②；根据1--2 >52-1>1-12，可得y 1<y 3<y 2，可判断③；根据题意可得关于x 的方程a x +1 x -3 =p p >0 的根即为抛物线与直线y =p p >0 的交点的横坐标，可判断④，即可．【解析】解：①∵图象对称轴为直线x =1，∴-b 2a=1，∴即2a +b =0，故①正确；②设w =am 2-b m +1 ，∴w =am 2-b m +1 =am 2+2a m +1 =am 2+2am +2a =a m +1 2+a ，∵二次函数y =ax 2+bx +c a ≠0 的图象开口向下，∴a <0，∴当m =-1时，w 取得最大值，最大值为a ，∴当m ≠1时，am 2-b m +1 <a ，故②正确；③∵点A -2,y 1 ，点B 12,y 2 ，点C 52,y 3 均在该图象上，且1--2 >52-1>1-12，∴y 1<y 3<y 2，故③正确；④∵图象过点-1,0 ，对称轴为直线x =1，∴抛物线与x 轴的另一个交点为3,0 ，∴抛物线的解析式为y =a x +1 x -3 ，∴关于x 的方程a x +1 x -3 =p p >0 的根即为抛物线与直线y =p p >0 的交点的横坐标，∴当p >0且抛物线与直线y =p p >0 的有两个交点，且交点的横坐标为整数时，这样的点P 有1个，∴关于x 的方程a x +1 x -3 =p p >0 的两根都是整数，则这样的p 值有1个，故④错误．故答案为：①②③【点睛】本题主要考查了二次函数的图象和性质，熟练掌握二次函数的图象和性质是解题的关键．三、单选题(共0分20(2023·浙江·校联考三模)已知点x 1，y 1 ，x 2，y 2 为二次函数y =-x 2图象上的两点(不为顶点)，则以下判断正确的是()A.若x 1>x 2，则y 1>y 2B.若x 1<x 2，则y 1<y 2C.若：x 1x 2<x 2 2，则y 1>y 2D.若x 1x 2>x 2 2，则y 1<y 2【答案】D【分析】根据二次函数的性质，逐一进行判断即可．【解析】解：∵y =-x 2，a =-1<0，对称轴为y 轴，∴在y 轴左侧，y 随x 的增大而增大，在y 轴右侧，y 随x 的增大而减小，抛物线上的点离对称轴越远，函数值越小；A 、x 1>x 2，y 1不一定大于y 2，例如x 1=1时，y 1=-1，x 2=-1时，y 2=-1，此时x 1>x 2，但是y 1=y 2；故选项A 错误；B 、x 1<x 2，y 1不一定小于y 2，例如x 1=-1时，y 1=-1，x 2=1时，y 2=-1，此时x 1<x 2，但是y 1=y 2；故选项B 错误；C 、当x 1x 2<x 2 2，y 1不一定大于y 2，例如x 1=-3时，y 1=-9，x 2=1时，y 2=-1，此时x 1x 2=-3<x 22=1，但是y1<y2；故选项C错误；D、当x1x2>x22，即：x1x2>x2x2>0，∴x1<x2<0或x1>x2>0，当x1<x2<0时，y1<y2，当x1>x2>0时，y1<y2，∴当x1x2>x22时，y1<y2；故选项D正确；故选D．【点睛】本题考查二次函数的图象和性质．熟练掌握二次函数的性质，是解题的关键．本题可以利用特殊值法进行排除，进行判断．21(2023·浙江杭州·统考二模)已知二次函数y1=(ax+1)(bx+1)，y2=(x+a)(x+b)，(a，b为常数，且ab≠0)，则下列判断正确的是()A.若ab<1，当x>1时，则y1>y2B.若ab>1，当x<-1时，则y1>y2C.若ab<-1，当x<-1时，则y1>y2D.若ab>-1，当x>1时，则y1>y2【答案】B【分析】先计算y1-y2=ax+1x+1x-1，再根据各选项给=ab-1x+bbx+1-x+a定的条件逐一分析即可得到答案．【解析】解：∵ab<1，x>1，∴ab-1<0，x-1>0，x+1>0，∴y1-y2=ax+1bx+1x+b-x+a=abx2+ax+bx+1-x2-ax-bx-ab=ab-1x2+1-ab=ab-1，x-1x+1∴y1-y2<0；∴y1<y2；故A不符合题意；∵ab>1，x<-1，∴ab-1>0，x-1<0，x+1<0，∴y1-y2>0；∴y1>y2；故B符合题意；∵ab<-1，x<-1，∴ab-1<0，x-1<0，x+1<0，∴y1-y2<0；∴y1<y2；故C不符合题意；∵ab>-1，x>1，∴ab-1>-2，x-1>0，x+1>0，∴y1-y2可以比0大，也可以比0小；∴y1，y2的大小不确定；故D不符合题意；故选B【点睛】本题考查的是二次函数的函数值的大小比较，因式分解的应用，熟练的利用作差的方法比较大小是解本题的关键．22(2023·浙江杭州·统考二模)点P m ,n 在二次函数y =ax 2-2ax a ≠0 的图象上，针对n 的不同取值，存在点P 的个数不同，甲乙两位同学分别得到如下结论：甲：若P 的个数为1，则n =-a ；乙：若P 的个数为2，则n ≥-a 则下列判断中正确的是()A.甲正确，乙正确B.甲正确，乙错误C.甲错误，乙正确D.甲错误，乙错误【答案】B【分析】根据抛物线的对称性可知，当n 是顶点的纵坐标时，P 的个数为1，当n 不是顶点纵坐标时，P 的个数为2，即可得出结论．【解析】解：∵y =ax 2-2ax =a x -1 2-a ，∴抛物线的顶点坐标为：1,-a ，∵点P m ,n 在二次函数y =ax 2-2ax a ≠0 的图象上，∴当n =-a 时，点P 为抛物线的顶点，只有1个，当n ≠-a 时，根据抛物线的对称性，点P 的个数为2；∴甲正确，乙错误；故选B ．【点睛】本题考查二次函数的图象和性质．熟练掌握抛物线的对称性，是解题的关键．23(2023·浙江宁波·校考二模)已知点A x 1，y 1 ，B x 2，y 2 在抛物线y =-(x -4)2+m (m 是常数)上．若x 1<4<x 2，x 1+x 2>8，则下列大小比较正确的是()A.y 1>y 2>mB.y 2>y 1>mC.m >y 1>y 2D.m >y 2>y 1【答案】C【分析】根据二次函数的性质得到抛物线y =-(x -4)2+m 的开口向下，有最大值为m ，对称轴为直线x =4，根据x 1<4<x 2，x 1+x 2>8，设A x 1,y 1 的对称点为A 1(x 0，y 1)，得出x 1+x 0=8，则在对称轴右侧，y 随x 的增大而减小，则当4<x 0<x 2时，m >y 1>y 2．【解析】解：∵y =-x -4 2+m ，∴a =-1<0，∴当x =4时，有最大值为y =m ，∴抛物线开口向下，∵抛物线y =-x -4 2+m 对称轴为直线x =4，设A x 1,y 1 的对称点为A 1(x 0，y 1)，即x 0>4，∴x 1+x02=4，∴x 1+x 0=8，∵x 1+x 2>8，∴x 1+x 2>x 1+x 0，∴x 2>x 0，∴4<x 0<x 2，∴m >y 1>y 2．故选：C ．【点睛】本题考查了二次函数图象上点的坐标特征：二次函数y =ax 2+bx +c (a ≠0)的图象为抛物线，则抛物线上的点的坐标满足其解析式；当a <0，抛物线开口向下；对称轴为直线x =-b2a，在对称轴左侧，y 随x 的增大而增大，在对称轴右侧，y 随x 的增大而减小．24(2023·统考二模)已知二次函数y =x 2+bx +c 过点A x 1,y 1 ，B x 1+t ,y 2 ，C x 1+2t ,y 3 三点．记m =y 2-y 1，n =y 3-y 2，下列命题正确的是()A.若n -m >2，则t <-1B.若n -m <2，则t >-1C.若t >1，则n -m >2D.若t <1，则n -m <2【答案】C【分析】根据题意求出m 和n ，再计算n -m ，再分别分析各选项即可得出真命题．【解析】解：由题意可得：m =y 2-y 1=x 1+t 2+b x 1+t +c -x 12+bx 1+c =x 1+t 2+b x 1+t -x 12-bx 1=t 2+2tx 1+bt n =y 3-y 2=x 1+2t 2+b x 1+2t +c -x 1+t 2+b x 1+t +c =x 1+2t 2+b x 1+2t +c -x 1+t 2-b x 1+t -c =3t 2+2tx 1+bt∴n -m =3t 2+2tx 1+bt -t 2+2tx 1+bt =2t 2，若n -m >2，则2t 2>2，∴t >1或t <-1，故A 是假命题；若n -m <2，则2t 2<2，∴-1<t <1，故B 是假命题；若t >1，则n -m =2t 2>2，故C 为真命题；若t <1，则0<2t 2<2，即0<n -m <2，故D 为假命题，故选C ．【点睛】本题考查了二次函数图像上的点，最值，解题的关键是将对应点代入，计算并化简得到n -m =2t 2．25(2023·浙江杭州·统考二模)已知y 关于x 的二次函数y =2mx 2+1-m x -1-m ，下列结论中正确的序号是()①当m =-1时，函数图象的顶点坐标为12,12；②当m ≠0时，函数图象总过定点：③当m >0时，函数图象在x 轴上截得的线段的长度大于32；④若函数图象上任取不同的两点P 1x 1,y 1 、P 2x 2,y 2 ，则当m <0时，函数在x >14时一定能使y 2-y 1x 2-x 1<0成立．A.①②③B.①③④C.②③④D.①②④【答案】A【分析】求出当m =-1时，二次函数图象的顶点坐标即可判断①；当m ≠0时，二次函数y =m 2x 2-x -1 +x -1，当2x 2-x -1=0时，y 的值与m 无关，求出x 的值，即可得到定点，即可判断。