空气动力学第三章不可压缩无粘流体平面势流

空气动力学基础前六章总结第一章 空气动力学一些引述1、 空气动力学涉及到的物理量的定义及相应的单位①压强：是作用在单位面积上的正压力，该力是由于气体分子在单位时间内对面发生冲击（或穿过该面）而发生的动量变化，具有点属性。

0,lim →⎪⎭⎫ ⎝⎛=dA dA dF p 单位：Pa, kPa, MPa 一个标准大气压：101kPa②密度：定义为单位体积内的质量，具有点属性。

0,lim →=dv dvdm ρ 单位：kg/㎡ 空气密度：1.225Kg/㎡③温度：反应平均分子动能，在高速空气动力学中有重要作用。

单位：℃ ④流速：当一个非常小的流体微元通过空间某任意一点的速度。

单位：m/s ⑤剪切应力：dy dv μτ= μ：黏性系数 ⑥动压：212q v ρ∞∞∞= 2、 空气动力及力矩的定义、来源及计算方法空气动力及力矩的来源只有两个：①物体表面的压力分布 ②物体表面的剪应力分布。

气动力的描述有两种坐标系：风轴系（L,D ）和体轴系(A,N)。

力矩与所选的点有关系，抬头为正，低头为负。

cos sin L N A αα=- ， s i n c o s D N A αα=+3、 气动力系数的定义及其作用气动力系数是比空气动力及力矩更基本且反映本质的无量纲系数，在三维中的力系数与二维中有差别，如：升力系数S q L C L ∞=（3D ），cq L c l ∞='（2D ）L L C q S ∞≡,D D C q S ∞≡,N N C q S ∞≡,A A C q S ∞≡,M M C q Sl ∞≡,p p p C q ∞∞-≡,f C q τ∞≡ 二维：S=C(1)=C4、 压力中心的定义压力中心，作用翼剖面上的空气动力，可简化为作用于弦上某参考点的升力L,阻力D 或法向力N ，轴向力A 及绕该点的力矩M 。

如果绕参考点的力矩为零，则该点称为压力中心，显然压力中心就是总空气动力的作用点，气动力矩为0。

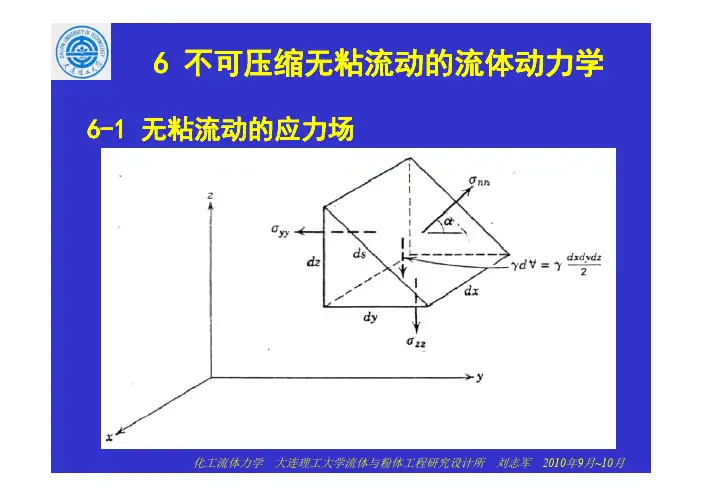
不可压缩无粘流动的流体动力学6 不可压缩无粘流动的流体动力学6无粘流动的应力场1 无粘流动的应力场6 1-1, z方向上微元质量应用牛顿第二定律,微元质量应用牛顿第二定律方程两边同除以dxdydz是微小量y方向的牛顿第二定律可以得出对运动的无粘流体而言，点的正应力各向对运动的无粘流体而言一点的正应力各向相同（即是一个标量），无粘流体中正应力等于热力学压强的负值，即等于热力学压强的负值无摩流动动方程欧方程无摩擦流动的动量方程：欧拉方程2 无摩擦流动的动量方程：欧拉方程6-2N S方程N-S方程在无摩擦流动中不存在剪应力，正应力是热力学压强的负值如果重力是唯一的质量力如果z坐标是垂直方向欧拉方程对于重力是唯的质量力的情况，柱对于重力是唯一的质量力的情况，柱坐标形式的分量方程如下：z轴是垂直向上的，因此，g r gθ，g z g=g=-做刚体运动的流体的欧拉方程3 做刚体运动的流体的欧拉方程6-3流体被加速而在相邻流体层之间没有相对运动，即，流体做没有变形的运动时，就不会产生剪应力。

运用合适的自由体动方程我们确定流体内体运动方程，我们可以确定流体内压强的变化。

的变化直线加速运动的流体绕着垂直轴线做稳定旋转运动的流体欧拉方程可以解决非惯性坐标系中做刚体运动的流体内压强分布的问题，可以得到相同的结果。

流线坐标中的欧拉方程6-44 流线坐标中的欧拉方程流线？定常流动中，流体质点的运动轨迹？流线坐标定常流动中，沿着流线：定常流动中，沿着流线的位移是用于描述运动方程较好的坐标坐标。

在非定常流动中，流线可以给出瞬在非定常流动中流线可以给出瞬时速度场的图形表示时速度场的图形表示。

运动方程可以写成沿着流线的位移坐标sn以及流线的法向位移坐标的表达式在流动方向上（即s方向）对体积为dsdndx的微元流体应用牛顿第二定律，并忽略粘性力β是流线的切线和水平方向的夹角αs 是流体质点沿着流线方向的加速度在流动方向上流体质点的随体加速度在具有垂直方向的z轴坐标系中沿着流线方向标系中，沿着流线方向对于定常流动，忽略质量力时，在流动方向上的欧拉方程速度的减小伴随着压强的增加，成反比关系。

第六章不可压缩流体的平面势流§ 6-1有势流动的速度势函数、速度势函数：对于无旋流动，有(1) 根据数学分析可知：上式成立是 udx 「dy • wdz 成为某一函数 (x, y ,z,t)的 全微分的充要条件。

，称为速度势函数，简称速度势。

即：d 二 udx dy wdzd 」dx dy dz 又有：x ■:y:zC^P.u =u = w =—x， ■y ，:z又由矢量分析:---- 汐-即-茯.V = ui i wk 二—i ——i — k excy cz即速度势的梯度等于流场的速度。

切向速度: 轴向速度：由此可见，'对任意方向的偏导数，就是速度V 在该方向的投影，这是'的 一个重要性质。

函数(x, y , z,t)称为速度势函数，简称速度势，对无旋流动 (rotV =0)，总有速度势存在，所以，无旋流动也称为有势流动。

在有势流动中，厂和「的关系为：…:wcv.z .:u:w ；:xdo :：u.x在柱坐标中：径向速度:■ rc rz■czB■一 BB『AB = .A V ds 二:A udx ： dy wdz = A d ：= B - ：A⑶即在有势流动中，沿AB 曲线的切向速度线积分（速度环量）等于终点B 与起 点A 的速度势之差。

又：在有势流动中，沿任一封闭周线K 的速度环量r = ■ V ds 二:K udx dy wdz =：« d :若「是单值或由斯托克斯定理，则 K^ =0、势函数方程郡PW —■:y ， :z 代入不可压流体连续方程: .u-w c.x :y :z 宀宀2 2则有：：：x 訶-2_ 2 2汶-:y :z称为拉普拉斯算子） （其中即在不可压流体的有势流动中，速度势 ，满足拉普拉斯方程。

凡是满足拉普拉斯方程的函数，数学上称为调和函数，所以，速度势点数是一个调和函数。

对柱面坐标，’的拉普拉斯方程为：1 二.丄二 c r 2r a r 胡2讯c<PU r = U J=〔推导过程为：将r ：丁，- rK ， z 江代入柱面坐标的连续方程，即可〕 根据以上讨论可知：只要流体流动无旋。