4.1平面向量的加法减法运算

平面向量的加法与减法在数学中，平面向量是用来描述平面上的位移和力的工具。

平面向量具有大小和方向两个特征，可以通过数学运算来完成加法和减法操作。

本文将详细介绍平面向量的加法和减法运算，并探讨其应用。

一、平面向量的表示方法平面向量通常用字母加箭头来表示，如AB→表示从点A到点B的位移向量。

平面向量还可以用坐标表示，如向量→AB的坐标表示为(ABx , ABy)。

其中，ABx表示向量在x轴上的分量，ABy表示向量在y轴上的分量。

二、平面向量的加法两个平面向量的加法是指将两个向量的对应分量相加的操作。

设有两个向量→AB和→CD，其坐标分别为(ABx , ABy)和(CDx , CDy)。

那么，向量→AB与→CD的和为→AB + →CD，其坐标为(ABx + CDx , ABy + CDy)，即两个向量的横坐标分量相加得到新向量的横坐标，纵坐标分量相加得到新向量的纵坐标。

三、平面向量的减法平面向量的减法是指将一个向量减去另一个向量的操作。

设有两个向量→AB和→CD，其坐标分别为(ABx , ABy)和(CDx , CDy)。

那么，向量→AB减去向量→CD的差为→AB - →CD，其坐标为(ABx - CDx , ABy - CDy)，即两个向量的横坐标分量相减得到新向量的横坐标，纵坐标分量相减得到新向量的纵坐标。

四、平面向量的应用平面向量的加法与减法在数学中有广泛的应用。

以下列举几个常见的应用场景：1. 位移问题：平面向量的加法可用于求解物体在空间中的位移问题。

通过将各个位移向量进行加法运算，可以得到物体的总位移向量。

2. 力的合成：力的合成是指多个力的作用下，合成后产生的力。

通过将各个力向量进行加法运算，可以得到合成力的大小和方向。

3. 航空航天：在航空航天领域中，平面向量的加法与减法被广泛运用于导航和控制系统中，用以计算飞行器的位置和速度。

4. 平面几何：平面向量的加法与减法在平面几何中也有重要应用。

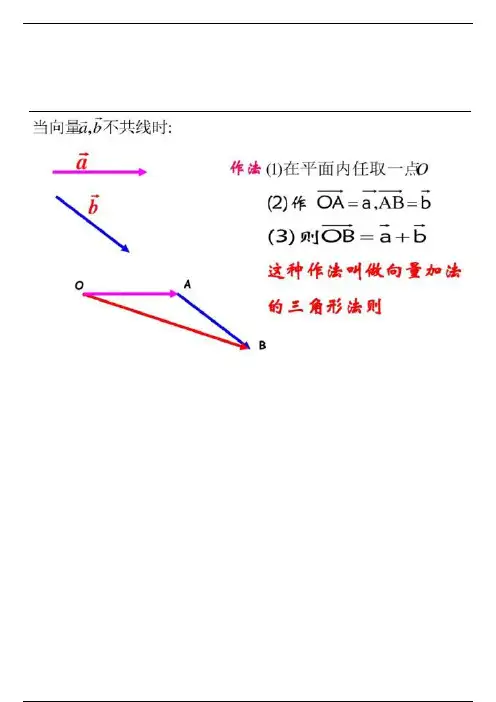
向量的加法口诀： 首尾相连，首连尾，方向指向末向量。

以第一个向量的起点为起点，以第二个向量的终点为终点的向量是两向量的和向量。

二、向量的减法两向量做减法运算，图像如下图所示：向量的减法口诀： 首首相连，尾连尾，方向指向被减向量。

以第一个向量的终点为起点，以第二个向量的终点为终点的向量是两向量的差向量。

向量的学习是高一数学必修四第二章的内容，要求同学们会向量的基本运算，其中就包括加法、减法、数乘。

要求大家能根据运算法则解决基本的向量运算，学会运用图像解决向量加减法，向量的数乘等问题。

向量的相关题目难度也不是很大，只要大家认真学习，认真做好笔记，认真做做题目，总结做题规律，那么当我们遇到类似题目时就会似曾相识，做起来也很顺手，再细心点的话，得满分也没有问题。

学习方法很多，重要的事找到适合自己的方法，当然适合自己方法就是最好的方法。

附一；三角形定则解决向量加减的方法将各个向量依次首尾顺次相接，结果为第一个向量的起点指向最后一个向量的终点。

注:两个向量相减，则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。

平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣＞1时,表示向量a的有向线段在原方向（λ＞0）或反方向（λ＜0）上伸长为原来的λ∣倍；当∣λ∣＜1时,表示向量a的有向线段在原方向（λ＞0）或反方向（λ＜0）上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律：(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律（第一分配律）：(λ+μ)a=λa+μa.数对于向量的分配律（第二分配律）：λ(a+b)=λa+λb.数乘向量的消去律：① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义：已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义：两个向量的数量积（内积、点积）是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉；若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示：a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a（交换律）；(λa)·b=λ(a·b)(关于数乘法的结合律)；（a+b)·c=a·c+b·c（分配律）；向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即：(a·b)·c≠a·(b·c)；例如：(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即：由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义：两个向量a和b的向量积（外积、叉积）是一个向量,记作a×b.若a、b不共线,则a×b的模是：∣a×b∣=|a|·|b|·sin〈a,b〉；a×b的方向是：垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质：∣a×b∣是以a和b为边的平行四边形面积.。

平面向量加法
两个向量做加法运算就是向量的加法，是一种向量的运算。

向量的加法口诀：首尾相连，首连尾，方向指向末向量。

向量的减法口诀：首首相连，尾连尾，方向指向被减向量。

平面向量是在二维平面内既有方向(direction)又有大小(magnitude)的量，物理学中也称作矢量，与之相对的是只有大小、没有方向的数量（标量）。

平面向量用a,b,c上面加一个小箭头表示，也可以用表示向量的有向线段的起点和终点字母表示。

向量的加法满足平行四边形法则和三角形法则。

AB+BC=AC。

a+b=(x+x'，y+y')。

a+0=0+a=a。

向量加法的运算律：交换律：a+b=b+a；结合律：(a+b)+c=a+(b+c)。

如果a、b是互为相反的向量，那么a=-b，b=-a，a+b=0. 0的反向量为0，AB-AC=CB. 即“共同起点，指向被减”，a=(x,y) b=(x',y') 则 a-b=(x-x',y-y')。

平面向量的基本概念与运算法则平面向量是在平面中具有大小和方向的量，由有序数对表示。

在数学中，平面向量是研究平面几何和代数的基础。

本文将介绍平面向量的基本概念和运算法则，以帮助读者更好地理解和应用平面向量。

一、平面向量的基本概念平面向量通常用有向线段表示，其中起点和终点之间的位置表示向量的方向。

一个平面向量可由其终点的坐标减去起点的坐标得到。

例如，向量AB可以表示为向量a = (x2-x1, y2-y1)，其中A(x1, y1)和B(x2, y2)是向量的起点和终点。

平面向量的大小通常用向量的长度来表示，也称为向量的模。

向量a = (x, y)的长度表示为|a|或||a||，可以通过勾股定理计算得到：|a| =√(x^2+y^2)。

向量的长度是一个非负数。

二、平面向量的运算法则1. 加法运算平面向量的加法运算定义为将两个向量的对应分量相加。

例如，对于向量a = (x1, y1)和向量b = (x2, y2)，它们的和可以表示为向量c = (x1+x2, y1+y2)。

2. 减法运算平面向量的减法运算定义为将两个向量的对应分量相减。

例如，对于向量a = (x1, y1)和向量b = (x2, y2)，它们的差可以表示为向量c =(x1-x2, y1-y2)。

3. 数乘运算平面向量的数乘运算定义为将向量的每个分量与一个标量相乘。

例如，对于向量a = (x, y)和标量k，它们的数乘可以表示为向量b = (kx, ky)。

4. 乘法运算平面向量的乘法运算有两种形式：数量积和向量积。

4.1 数量积数量积（又称点积或内积）定义为两个向量的对应分量相乘后再相加。

数量积的结果是一个标量。

对于向量a = (x1, y1)和向量b = (x2,y2)，它们的数量积表示为a · b = x1x2 + y1y2。

4.2 向量积向量积（又称叉积或外积）定义为两个向量的乘积是一个新的向量，它垂直于原来两个向量组成的平面，并且方向遵循右手法则。

平面向量的加法与减法在平面向量的运算中，加法和减法是两个基本且重要的运算操作。

通过合适的方法进行向量相加或相减，可以获得新的向量，进而帮助我们解决实际问题和优化计算过程。

本文将重点探讨平面向量的加法和减法，并介绍它们的性质和运算规则。

一、向量的表示平面上的向量可以用有序数对表示，我们通常以大写字母加箭头（→）来表示向量，例如向量A可以表示为A→ = (x,y)。

其中，x和y分别表示向量在x轴和y轴上的分量。

二、向量的加法向量的加法是指将两个向量相加，得到一个新的向量。

向量的加法满足以下几个性质：1. 交换律：对于任意向量A和B，有A + B = B + A。

2. 结合律：对于任意向量A、B和C，有(A + B) + C = A + (B + C)。

3. 零向量：零向量的表示为O→ = (0,0)，对于任意向量A，有A +O→ = A。

根据以上性质，我们可以通过向量的对应分量相加的方式来进行向量的加法运算。

例如，向量A→ = (x1,y1)和向量B→ = (x2,y2)，它们的和A→ + B→ = (x1+x2,y1+y2)。

三、向量的减法向量的减法是指将一个向量减去另一个向量，得到一个新的向量。

向量的减法同样满足交换律和结合律，减法的规则可以通过相应的加法来表示。

对于向量A和向量B，向量的减法可以表示为A→ - B→ = A→ + (-B→)，其中-A→表示向量B→的反向量。

向量的反向量的表示为-A→ = (-x,-y)，即将向量的每个分量取反。

根据向量的加法运算规则，我们可以将向量的减法转化为相应的加法运算。

例如，向量A→ = (x1,y1)和向量B→ = (x2,y2)，它们的差A→ - B→ = A→ + (-B→) = (x1,y1) + (-x2,-y2) = (x1-x2,y1-y2)。

四、几何意义向量的加法和减法在平面几何中具有重要的几何意义。

对于向量的加法，可以将两个向量的起点放在同一个位置，然后将终点相连，所得的新向量即为其和向量。

平面向量的加减法运算教学设计以平面向量的加减法运算为主题的教学设计第一节：引入引导学生回顾平面向量的定义和性质，强调向量的表示方法和运算规则。

简要介绍平面向量的加法和减法运算，以及它们的几何意义。

第二节：平面向量的加法运算1.1 向量的加法定义向量的加法是指将两个向量的对应分量相加得到一个新的向量。

引导学生根据定义进行向量的加法运算。

1.2 加法运算的性质向量的加法满足交换律、结合律和零向量的存在性。

通过示例和练习题让学生理解和应用这些性质。

1.3 加法运算的几何意义向量的加法可以用平行四边形法则来解释，即将两个向量的起点相连，得到一个新的向量，它的起点和终点分别为原向量的起点和终点。

第三节：平面向量的减法运算2.1 向量的减法定义向量的减法是指将第二个向量取负后与第一个向量进行加法运算。

引导学生根据定义进行向量的减法运算。

2.2 减法运算的性质向量的减法满足减去一个向量等于加上其相反向量，即a-b=a+(-b)。

通过示例和练习题让学生理解和应用这个性质。

2.3 减法运算的几何意义向量的减法可以用平行四边形法则来解释，即将第二个向量的起点与第一个向量的终点相连，得到一个新的向量，它的起点和终点分别为原向量的起点和第二个向量的终点。

第四节：应用练习通过一些实际问题和练习题，让学生应用所学的平面向量的加减法运算解决几何和物理问题。

可以设计一些场景，如力的合成、位移的计算等。

第五节：总结与拓展对平面向量的加减法运算进行总结，强调运算的规则和性质，以及几何意义。

鼓励学生进一步拓展应用平面向量的知识，如向量的数量积和向量的夹角等。

通过以上教学设计，可以帮助学生系统掌握平面向量的加减法运算，理解其几何意义，并能够应用于实际问题的求解。

同时，通过练习和拓展，培养学生的问题解决能力和数学思维。

向量公式汇总平面向量1、向量的加法向量的加法满足平行四边形法则和三角形法则。

AB+BC=AC。

a+b=(x+x'，y+y')。

a+0=0+a=a。

向量加法的运算律：交换律：a+b=b+a；结合律：(a+b)+c=a+(b+c)。

2、向量的减法如果a、b是互为相反的向量，那么a=-b，b=-a，a+b=0. 0的反向量为0 AB-AC=CB. 即“共同起点，指向被减”a=(x,y) b=(x',y') 则a-b=(x-x',y-y').3、数乘向量实数λ和向量a的乘积是一个向量，记作λa，且∣λa∣=∣λ∣•∣a∣。

当λ＞0时，λa与a同方向；当λ＜0时，λa与a反方向；当λ=0时，λa=0，方向任意。

当a=0时，对于任意实数λ，都有λa=0。

注：按定义知，如果λa=0，那么λ=0或a=0。

实数λ叫做向量a的系数，乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩。

当∣λ∣＞1时，表示向量a的有向线段在原方向（λ＞0）或反方向（λ＜0）上伸长为原来的∣λ∣倍；当∣λ∣＜1时，表示向量a的有向线段在原方向（λ＞0）或反方向（λ＜0）上缩短为原来的∣λ∣倍。

数与向量的乘法满足下面的运算律结合律：(λa)•b=λ(a•b)=(a•λb)。

向量对于数的分配律（第一分配律）：(λ+μ)a=λa+μa.数对于向量的分配律（第二分配律）：λ(a+b)=λa+λb.数乘向量的消去律：①如果实数λ≠0且λa=λb，那么a=b。

②如果a≠0且λa=μa，那么λ=μ。

4、向量的的数量积定义：已知两个非零向量a,b。

作OA=a,OB=b,则角AOB称作向量a和向量b 的夹角，记作〈a,b〉并规定0≤〈a,b〉≤π定义：两个向量的数量积（内积、点积）是一个数量，记作a•b。

若a、b不共线，则a•b=|a|•|b|•cos〈a，b〉；若a、b共线，则a•b=+-∣a∣∣b∣。

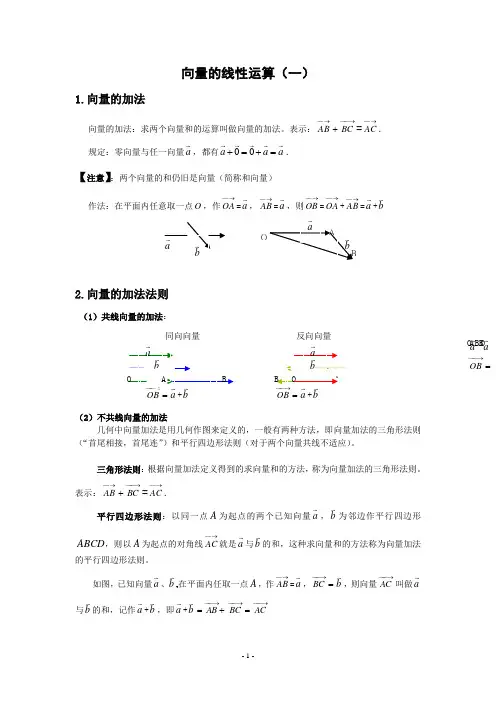
ABabbaa a O =−→−OBA B O B a abb=−→−OB a +b ABAa +b向量的线性运算（一）1.向量的加法向量的加法：求两个向量和的运算叫做向量的加法。

表示：→--AB −→−+BC =→--AC ．规定：零向量与任一向量a ，都有00a a a +=+=．【注意】：两个向量的和仍旧是向量（简称和向量）作法：在平面内任意取一点O ，作→--OA =a →--→--OB =→--OA +→--AB a +b2.向量的加法法则（1）共线向量的加法：同向向量反向向量（2）不共线向量的加法几何中向量加法是用几何作图来定义的，一般有两种方法，即向量加法的三角形法则（“首尾相接，首尾连”）和平行四边形法则（对于两个向量共线不适应）。

三角形法则：根据向量加法定义得到的求向量和的方法，称为向量加法的三角形法则。

表示：→--AB −→−+BC=→--AC ．平行四边形法则：以同一点A 为起点的两个已知向量a ，b 为邻边作平行四边形ABCD ，则以A 为起点的对角线→--AC 就是a 与b 的和，这种求向量和的方法称为向量加法的平行四边形法则。

如图，已知向量a 、b 在平面内任取一点A ，作→--AB =a ，=−→−BC b ，则向量−→−AC 叫做a与b 的和，记作a +b ，即a +b +=−→−AB =−→−BC −→−AC【说明】：教材中采用了三角形法则来定义，这种定义，对两向量共线时同样适用，当向量不共线时，向量加法的三角形法则和平行四边形法则是一致的 特殊情况：探究：（1）两相向量的和仍是一个向量；（2）当向量a 与b 不共线时，a +b 的方向不同向，且|a +b |<|a |+|b |; （3）当a 与b 同向时，则a +b 、a 、b 同向，且|a +b |=|a |+|b |,当a 与b 反向时，若|a |>|b |,则a +b 的方向与a 相同，且|a +b |=|a |-|b |；若|a |<|b |,则a +b 的方向与b 相同，且|a +b |=|b |-|a |.（4）“向量平移”：使前一个向量的终点为后一个向量的起点，可以推广到n 个向量连加3.向量加法的运算律（1）向量加法的交换律：a +b =b +a（2）向量加法的结合律：(a +b ) +c =a +(b +c ) 证明：如图：使=−→−AB a , =−→−BC b , =−→−CD c 则(a +b )+c =−→−AC +=−→−CD −→−AD ，a + (b +c )=−→−AB −→−+BD −→−=AD ,∴(a +b )+c =a +(b +c )从而，多个向量的加法运算可以按照任意的次序、任意的组合来进行例如：()()()()a b c d b d a c +++=+++；[()]()a b c d e d a c b e ++++=++++．例题：例1. O 为正六边形的中心，作出下列向量：（1）−→−OA +−→−OC （2）−→−BC +−→−FE （3）−→−OA +−→−FE例2．如图，一艘船从A 点出发以h km /32的速度向垂直于对岸的方向行驶，同时水aaab bba +ba +b ABC ABCD三角形法则平行四边形法则的流速为h km /2，求船实际航行的速度的大小与方向。

平面向量的加减平面向量是指在二维平面上具有大小和方向的量，通常用箭头表示。

在平面向量的运算中，加法和减法是最基本且常见的操作。

本文将主要介绍平面向量的加法和减法，并提供相关的例题进行讲解。

一、平面向量的加法平面向量的加法可以理解为将两个向量按照一定规律进行合并的过程。

具体来说，对于两个平面向量A和B，它们的加法运算可以表示为A + B = C，其中C为两个向量相加得到的结果。

在平面向量的加法中，可以利用平行四边形法则或三角形法则来进行计算。

下面我们以平行四边形法则为例进行说明。

1. 平行四边形法则平行四边形法则是指将两个向量的起点放在同一点，然后将它们的向量箭头相连，形成一个平行四边形。

向量C的起点为平行四边形的共同起点，终点为与该点对应的平行四边形对角线的另一个端点。

图示如下：（插入平行四边形示意图）2. 平面向量的加法性质在平面向量的加法中，有以下几个性质：- 交换律：对于任意平面向量A和B，有A + B = B + A。

- 结合律：对于任意平面向量A、B和C，有(A + B) + C = A + (B + C)。

- 零向量：平面上的零向量O满足A + O = A，对于任意平面向量A。

二、平面向量的减法平面向量的减法可以理解为通过改变向量的方向和大小，使得两个向量相减得到一个新的向量。

具体来说，对于两个平面向量A和B，它们的减法运算可以表示为A - B = D，其中D为两个向量相减得到的结果。

在平面向量的减法中，可以利用向量加法的性质进行计算。

具体做法是将B取负后与A相加，即A - B = A + (-B)。

下面我们通过一个例题来进行说明。

例题：已知向量A = 3i + 2j，向量B = 5i - 4j，求向量C = A - B的结果。

解：首先将向量B取负得到-B = -5i + 4j，然后利用向量加法进行计算，有：C = A + (-B)= (3i + 2j) + (-5i + 4j)= (3i + (-5i)) + (2j + 4j)= -2i + 6j因此，向量C的结果为-2i + 6j。

平面向量加乘法除法口诀
一、向量的加法
两个向量做加法运算就是向量的加法，是一种向量的运算。

首先我们来看图像。

向量加法图像
向量的加法口诀：首尾相连，首连尾，方向指向末向量。

二、向量的减法
两向量做减法运算，图像如下图所示：
向量的减法图像
向量的减法口诀：首首相连，尾连尾，方向指向被减向量。

向量的学习是高一数学必修四第二章的内容，要求同学们会向量的基本运算，其中就包括加法、减法、数乘。

要求大家能根据运算法则解决基本的向量运算，学会运用图像解决向量加减法，向量的数乘等问题。

向量的相关题目难度也不是很大，只要大家认真学习，认真做好笔记，认真做做题目，总结做题规律，那么当我们遇到类似题目时就会似曾相识，做起来也很顺手，再细心点的话，得满分也没有问题。

学习方法很多，重要的事找到适合自己的方法，当然适合自己方法就是最好的方法。

最后祝同学们学业有成，更上一层楼。

向量加减法运算
向量加法满足和三角形法则。

向量加法的运算律有交换律：
a+b=b+a；：(a+b)+c=a+(b+c)。

向量减法的运算法则为：如果a、b是互为相反的向量，那么a-b=0。

在数学中，向量（也称为向量、几何向量、矢量），指具有大小和方向的量。

它可以形象化地表示为带箭头的线段。

向量定义是既有大小，又有方向的量叫做向量。

在几何上，向量用有向线段来表示，有向线段长度表示向量的大小，有向线段的方向表示向量的方向。

其实有向线段本身也是向量，称为几何向量。

在实际问题中，有些向量与其起点有关，有些向量与其起点无关。

由于一切向量的共性是它们都有大小和方向，所以在数学上我们只研究与起点无关的向量，并称这种向量为自由向量（以后简称向量），即只考虑向量的大小和方向，而不论它的起点在什么地方。

在只讨论自由向量的约定下，向量可以平行移动，所以两个向量相等的定义如下：定义如果两个向量大小相等，且方向相同，我们就说这两个向量是相等的。

即：经过平行移动后能完全重合的向量是相等向量，或者说它们是同一个向量。

平面向量的所有公式平面向量是研究平面上的有大小和方向的量，它有三个基本组成部分：模、方向和位移。

在平面向量的运算中，有加法、减法、数量乘法和点乘法等基本运算法则。

平面向量的计算公式如下：一、向量的模：向量的模即向量的长度，用，AB，表示，A、B为向量的起点和终点。

根据两点之间的距离公式，向量AB的长度为：，AB，= sqrt((x2-x1)^2 + (y2-y1)^2)二、向量的方向角：向量的方向角用θ表示，θ的计算公式为：θ = arctan(y/x)三、向量的加法：向量的加法可用平行四边形法则或三角形法则进行运算。

-平行四边形法则：若AB向量与CD向量首位相连，则它们的和向量AC的终点D与向量CD的终点D形成一条与中点O1O2平行的平行线。

-三角形法则：若AB向量与BC向量首位相连，则它们的和向量AC的起点A与向量AB的起点A和向量BC的起点B重合，且终点C与向量BC的终点C重合。

四、向量的减法：向量的减法可用向量加法的逆运算进行。

若向量AB与向量CD首位相连，则它们的差向量AC的终点C与向量CD的起点C重合。

即向量减法A-B=A+(-B)，其中-B是向量B的逆向量。

五、数量乘法：向量与标量的乘法可分为两种情况。

-正数乘法：若k为正数，则k倍数的向量k·A与A方向相同，长度为原向量长度的k倍。

-负数乘法：若k为负数，则k倍数的向量k·A与A方向相反，长度为原向量长度的，k，倍。

六、数量积(点乘法)：数量积是向量积的另一种形式，它用于计算两个向量之间的夹角以及向量在一些方向上的投影。

-数量积的计算：设A(x1,y1)和B(x2,y2)是平面上的两个向量，它们的数量积为：A·B=x1*x2+y1*y2- 夹角的计算：设向量A(x1, y1)和B(x2, y2)的夹角为θ，则夹角的余弦为：cosθ = (A·B) / (，A， * ，B，)- 向量在一些方向上的投影：设向量A的模为，A，θ为A与一些方向的夹角，则A在该方向上的投影为：P = ，A，* cosθ以上是平面向量的一些基本计算公式。

平面向量及其运算平面向量是指在平面上用箭头表示的量，具有大小和方向。

在数学中，平面向量的运算包括加法、减法、数量乘法和向量点积。

一、向量的表示平面向量通常用有箭头的字母表示，例如a、b等。

向量的起点为初始点，箭头的指向表示向量的方向。

向量的大小可以用线段的长度来表示。

二、向量的加法向量的加法是指将两个向量首尾相接，然后连接起点和终点的线段就是它们的和向量。

加法满足交换律和结合律，即a + b = b + a，(a + b) + c = a + (b + c)。

三、向量的减法向量的减法是指将被减向量反向后与减向量相加。

减法可以转化为加法的形式，即a - b = a + (-b)。

四、数量乘法向量与一个实数相乘，称为数量乘法。

数量乘法改变向量的大小和方向。

当实数为正数时，向量与实数的乘积与向量的方向相同；当实数为负数时，向量与实数的乘积与向量的方向相反。

五、向量的点积向量的点积是指相互垂直的两个非零向量的数量积。

点积的结果是一个实数。

设a = (a1, a2)和b = (b1, b2)，则a·b = a1 * b1 + a2 * b2。

六、向量的运算性质1. 向量加法满足交换律和结合律。

2. 数量乘法满足结合律和分配律。

3. a·b = b·a，a·(kb) = k(a·b)，(a + b)·c = a·c + b·c。

七、平面向量的应用平面向量在几何、物理等学科中有着广泛的应用。

以下是一些应用场景：1. 平面向量可以用来描述物体在平面上的位移和速度。

2. 平面向量可以用来表示力的大小和方向，从而研究物体在平面上的受力情况。

3. 平面向量可以用来解决几何问题，如判断线段是否平行、垂直等。

总结：平面向量是具有大小和方向的量，在数学中有着广泛的应用。

平面向量的运算包括加法、减法、数量乘法和向量点积。

通过理解和掌握向量的运算法则，我们可以更好地应用平面向量解决问题，在几何、物理等领域中有着重要的作用。

平面向量的运算平面向量是指在特定的二维空间中，包含一个方向和大小的矢量。

它们可以用来描述物体在空间中的位置，也可以用来表示一个方向。

平面向量还可以用来表示力，热量和速度等物理量。

平面向量可以用不同的方式表示。

一种常见的表示方式是用“箭头法”，即在任意两点之间画出一条箭头，由起点指向终点，来表示方向和大小。

也可以用一个由两个向量表示的矢量来表示一个平面向量，这一种表示方式称为“极坐标系表示法”。

二、平面向量的四则运算平面向量可以进行四则运算，即加法、减法、乘法和除法。

（1）平面向量的加法运算平面向量的加法运算是指将两个平面向量的终点相加得到的向量。

如果平面向量的表示方式是极坐标系表示法，只需要将两个向量的模和方向加起来即可。

（2）平面向量的减法减法的运算方式跟加法一样，只需要将被减数的终点减去减数的终点，即可得到减法结果。

（3）平面向量的乘法乘法是指将平面向量与一个标量相乘得到新的平面向量，新的平面向量方向和原向量一致，但是大小不同。

（4）平面向量的除法除法是指将平面向量与一个标量相除得到的新的平面向量，新的平面向量的方向与原向量相反，但是大小不同。

三、平面向量的应用1、研究角度平面向量可以用来研究各种物理现象，如抛物运动及其分析，曲率等。

2、工程中的应用平面向量在工程中有着重要的应用，如在航空、船舶、汽车等工程中，都可以应用平面向量来研究物体的运动轨迹。

3、社会经济中的应用平面向量可以应用于社会经济学中，如解决资源分配问题、多人博弈中的最优策略等。

总结本文主要讨论了平面向量的概念、四则运算以及其应用。

平面向量可以用箭头法或极坐标系表示法来表示，它们可以进行加减乘除四则运算，在物理、工程和社会经济中都有重要的应用。