【全国通用】六年级下册数学思维训练(55)

小学奥数思维训练全国通用题库赛前冲刺1000题（五）1、某工程队修筑一条公路，按照计划派出了32的人连续施工30天，完成了这项工程的60%。

之后为了加快施工进度，从剩余人中再派出10人支援，结果比原计划提前5天完成。

问该工程队共有多少人？A.30B.45C.60D.902、某单位计划从周一至周五中选出3天，安排员工到甲、乙、丙三个城市考察学习，每个城市考察1天。

因特殊原因，甲、乙两个城市不能在相邻的两天被考察，问有多少种不同的安排方式？A.18B.30C.36D.603、某公司为了加强企业内部文化交流并提升员工的归属感，特制作了500件企业文化衫，共有M 、L 、XL 、XXL 和XXXL 五种尺寸。

其中穿M 号的有48人，是穿XXXL 号人数的2倍，穿XL 号的人数排名第一，且与穿L 号的人数之和比穿XXL 号人数的2倍少76人。

问穿L 号的人数最多有多少人？A.94B.93C.92D.915、一超市和某罐头加工厂签订合作协议，每月要求该厂提供3000瓶罐头，每瓶罐头的进货单价为6元，若单价每降低0.2元，则超市就多进货200瓶。

问：该罐头厂每月可获得的最大收入是多少元？A.20250B.20240C.20000D.180006、有两节车厢的货物需要搬运，一组工人先搬了第一节车厢货物的31，然后分出一半的人手去第二节车厢搬运货物，当第一节车厢还剩下最初货物的31时，又分出一半的人手去搬运第二节车厢的货物，最后两节车厢的货物同时搬完。

问第二节车厢的货物数量比第一节车厢：A.多31B.少31C.多41D.少417、某校甲、乙、丙、丁4人参加省级奥林匹克数学竞赛，获奖的概率依次为80%、75%、60%和50%，若乙只能和甲同时获奖，问该校参加比赛的4人中恰有2人获奖的概率为：A 、23.5%B 、26.5%C 、28%D 、31%8、由于基础设备、人力等成本因素，服装厂的单位利润和出货量的大小相关，出货量低于50万元时利润率为20%；低于或等于100万元，高于50万元的部分利润率为40%；高于100万元的部分利润率为50%。

六年级数学下册思维训练题(含答案)六年级数学下册思维训练题1、 ( )2、在每个( )中填入一个数，使下面的一列数从第3个数开始，每一个数等于前面两个数的和，则第10个数是( )。

( )，( )，( )，( )，8，( )，( )，( )，55，( )，3、六年级数学下册思维训练题：高位数字大于低位数字的四位数 (acd)有( )个。

4、下面四个图形都是正方体的展开图，其中每个正方形都标上了颜色。

已知正方体相对的两个面上的颜色相同，那给出的展开图中不正确的是( ).(填序号)5、春节联欢晚会时，2019盏彩灯(各由一个拉线开关控制)大放光明。

小真把编号是6的倍数的开关各拉一次，小聪把编号是19的倍数的开关各拉一次，小明把编号是29的倍数的开关各拉一次。

这时有( )盏彩灯是亮的。

6、甲、乙、丙、丁四人共同购买了一台液晶电视。

已知甲出的钱是其它三人总钱数的，乙出的钱是其余三人总钱数的，丙出的钱是其余三人总钱数的，丁出了2070元，则这台电视的价格是( )元。

7、设两个两位数的积是一个四位数的算式贝贝京京=北京欢迎中的文字代表数字1，2，3，4，5，相同文字表示相同的数字那么，贝京=( );四位数北京欢迎=( )。

8、已知五位数能被2019整除，则除得的商是( )。

9、如图，在三角形ABC中，角A=80度，BD=BE,CD=CF,则角EDF=( )度?10、有三个圆心相同的半圆，它们的直径分别为1、3、5，用线段将其分割成9块，如图所示，如果每块中的字母代表着这一块面积，并且相同字母表示相同的面积,那么A:B=( )。

11、如图，三角形ABC的面积是240平方厘米，D是AC的中点，E是BC的三等分点，则阴影部分的面积=( )平方厘米.12、小强骑自行车从甲地到乙地需要3小时，如果先步行2千米，步行速度是骑车速度的，则晚到20分钟，那么甲，乙两地相距多少千米?13、如图，A、B是圆的直径的两端，甲在A点，乙在B点同时出发反向而行，两人在C点第一次相遇，在D点第二次相遇。

第一讲立体图形及展开同学们在五年级所学习的立体图形主要是长方体和正方体，从这一讲开始我们将一起研究数学竞赛中经常出现的有关长方体和正方体的问题,帮助大家提高观察能力和空间想像能力，以及掌握解答问题的技巧和方法。

这一讲我们进一步研究长方体和正方体的特征及展开图例题选讲例1：图1所示的是一个正方体纸盒拆开后平摊在桌面上的形状。

如果将这个展开图恢复成原来的正方体,图中的点F、点G分别与哪个点重合?【分析与解答】为了研究方便,我们将正方体六个面分别标上序号1、2、３、４、5、6,如果将l作为底面,那么4就是后面,5为右面,6为前面,2则是左面，3就是上面,(如图２)。

从图中不难看出点F与点Ｎ，重合,点G与点Ｓ重合。

还有一种方法就是动手制作一张展开图,折一折,结果就一目了然了，同学们不妨试试吧！例2:一只小虫从图l所示的长方体上的A点出发,沿长方体的表面爬行,依次经过前面、上面、后面、底面，最后到达P点。

请你为它设计一条最短的爬行路线。

【分析与解答】因为小虫在长方体的表面爬行,所以我们可以将长方体的前、后、上、下西个面展开成平面图形(如图2)。

又因为在平面上“两点之间的线段长度最短”,所以连接AP，则线段ＡP为小虫爬行的最短路线。

练习与思考1．如图所示的是一个正方体纸盒拆开后平摊在桌面上的形状。

如果将这个展开图恢复成原来的正方体，图中的点B、点D分别与哪个点重合？2．如图所示的是一个棱长3厘米的正方体木块,一只蚂蚁从Ａ点沿表面爬向B点。

请画出蚂蚁爬行的最短路线。

问：这样的路线共有几条?３.将一张长方形硬纸片，剪去多余部分后,折叠成一个棱长为l厘米的正方体。

这张长方形硬纸片的面积最小是多少平方厘米?4.一块长方形的铁皮,长2８厘米，在这块铁皮的四角各剪下一个边长为4厘米的小正方形，然后通过折叠、焊接做成一个无盖的长方体盒子。

已知这个盒子的容积是9６0立方厘米,求原来长方形铁皮的面积。

5.如图所示的是一个正方体木块的表面展开图，若在正方体的各面填上数,使其对面两数之和为7,则A、B、c处填的数各是多少？第二讲长方体和正方体的表面积在数学竞赛中，有许多问题涉及到长方体和正方体表面积的计算。

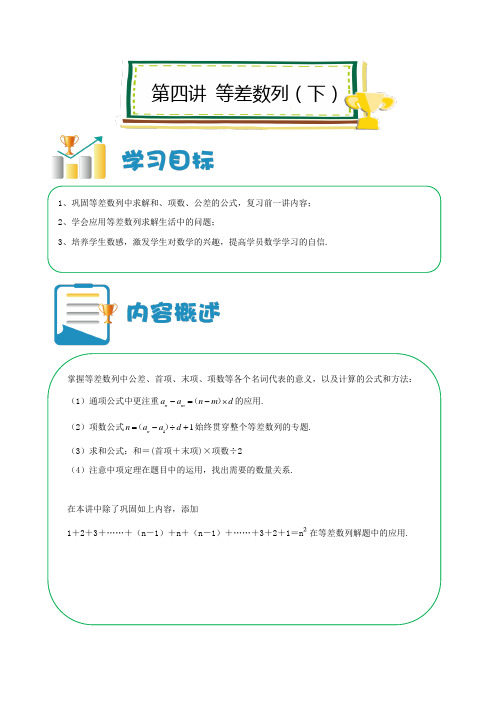
第四讲等差数列（下）1、巩固等差数列中求解和、项数、公差的公式，复习前一讲内容；2、学会应用等差数列求解生活中的问题；3、培养学生数感，激发学生对数学的兴趣，提高学员数学学习的自信.掌握等差数列中公差、首项、末项、项数等各个名词代表的意义，以及计算的公式和方法：（1）通项公式中更注重n ma a n m d-=-⨯（）的应用.（2）项数公式11nn a a d=-÷+（）始终贯穿整个等差数列的专题.（3）求和公式：和＝(首项＋末项)×项数÷2（4）注意中项定理在题目中的运用，找出需要的数量关系.在本讲中除了巩固如上内容，添加1＋2＋3＋……＋（n－1）＋n＋（n－1）＋……＋3＋2＋1＝n²在等差数列解题中的应用.兔读一本书，第一天读30页，从第二天起，每天读的页数都必须比前一天多4页，最后一天读了70页刚好读完，这本书共有几页？【解析】先求小红看了几天，（70－30）÷4＋1＝11天，再求这本书总页数：（30＋70）×11÷2＝550页. 解答：这本书共有550页.计算：1＋2＋3＋……＋19＋20＋19＋……＋3＋2＋1【解析】方法一：分两个等差数列求和计算，（1＋20）×20÷2＋（19＋1）×19÷2＝400.方法二：1＋2＋3＋……＋(n-1)＋n ＋(n-1)＋……＋3＋2＋1＝n ²，20×20＝400.解答：1＋2＋3＋……＋19＋20＋19＋……＋3＋2＋1＝400.把210拆成7个自然数的和，使这7个数从小到大排成一行后，相邻两个数的差都是5，那么，第1个数与第6个数分别是多少？【解析】由题可知：由210拆成的7个数一定构成等差数列，则中间一个数为210÷7＝30，所以，这7个讲演者：得分：讲演者：得分：数分别是15，20，25，30，35，40，45.解答：第1个数是15，第6个数是40.编号为1-9的九个盒子中共放有351颗小玻璃珠，除编号为1的盒子外，每个盒子里的小玻璃珠都比前一号盒子多同样多的颗数.（1）如果1号盒子内放有11颗小玻璃珠，那么后面的盒子比它前一号的盒子多放几颗？（2）如果3号盒子内放了23颗小玻璃珠，那么8号盒子中放了几颗？【解析】根据等差数列的中项定理：最中间的盒子5号盒子颗数是351÷9＝39.（1）公差＝（39－11）÷（5－1）＝7；（2）公差＝（39－23）÷（5－3）＝8，8号盒子＝23＋（8－3）×8＝63.解答：（1）7颗；（2）63颗.计算：4＋5＋6＋……＋98＋99＋98＋97＋……＋5＋4＋3【解析】使用1＋2＋3＋……＋(n-1)＋n＋(n-1)＋……＋3＋2＋1＝n²这个公式求解.解答：原式＝99×99－1－2－3－2－1＝9801－9＝9792.小王和小李同时开始工作，小王第一个月得到1000元工资，以后每个月多得60元；小高第一个月得到500元工资，以后每月多得45元.两人工作一年后，所得工资总数相差多少元？【解析】方法一：小王一年工资总和是1000×12＋60＋60×2＋60×3＋……＋60×11＝12000＋60×（1＋2＋3＋……＋11）＝12000＋3960＝15960；小李一年工资总和是500×12＋45＋45×2＋45×3＋……＋45×11＝6000＋45×（1＋2＋3＋……＋11）＝6000＋2970＝8970；两人工资总数相差15960－8970＝6990. 方法二：第一个月两个人的工资差是500元，第二个月两个人的工资差是500＋15，第三个月两个人的工资差是500＋15×2，以此类推，第12个月两个人的工资差是500＋15×11.工资总数相差：500×11＋15×（1＋2＋3＋……＋11）＝5500＋990＝6990.解答：两人工作一年后，所得工资总数相差6990元.魔术师表演魔术，刚开始，桌上的盒子里放着3个乒乓球，第一次，他从盒子里拿出1个球，把它变成3个后全部放回盒子里；第二次，他从盒子里拿出2个球，把每个球变成3个后，又全部放回盒子里，……，第十次他从盒子里拿出10个球，把每个球变成3个后，再全部放回盒子里.请你算一算，现在盒子里一共有多少个兵乓球？【解析】方法一：魔术师第一次，拿出1个放回3个，实际上多了2个；第二次，拿出2个放回3×2个，实际上多了2×2个；以此类推；第十次，拿出10个放回3×10个，实际上多了2×10个.一共多了2＋2×2＋……＋2×10＝2×（1＋2＋……＋10）＝110，一共有110＋3＝113个.方法二：魔术师总共拿出来的乒乓球数是1＋2＋……＋10＝55，放回去的总数是3×（1＋2＋……＋10）＝＝165，一共有3＋165－55＝113个.解答：现在盒子里一共有113个兵乓球.已知一个等差数列的前15项的和为450，前20项的和为750，请问：这个等差数列的公差是多少？首项是多少？【解析】方法一：由等差数列的求和公式可知：首项＋末项＝和×2÷项数，所以第1项＋第15项＝450×2÷15＝60，第1项＋第20项＝750×2÷20＝75；所以第20项和第15项相差75－60＝15，公差＝15÷（20－15）＝3；第15项与第1项的差是3×（14－1）＝42，根据和差问题，第一项＝（60－42）÷2＝9.方法二：有等差数列的中项定理可知，前15项的中间项是第8项＝450÷15＝30；前20项750，那么后5项的和为750－450＝300，所以第18项为300÷5＝60；从而求出公差＝（60－30）÷（18－8）＝3.首项＝30－（8－1）×3＝9.解答：这个等差数列的公差是3，首项是9.计算：260－1－2－3－4－……－19－20【解析】解答：原式＝260－（1＋2＋3＋4＋……＋19＋20）＝50兔从七月一日开始写毛笔字，第一天写了6个，以后每天比前一天多写相同数量的毛笔字，结果全月共写1116个毛笔字，兔每天比前一天多写几个毛笔字？【解析】根据等差数列的中项定理：第16天写毛笔字1116÷31＝36（个）；那么，兔每天比前一天多写（36－6）÷（16－1）＝2（个）毛笔字.解答：兔每天比前一天多写2个毛笔字.黑白两种颜色的珠子，一层黑，一层白，排成正三角形的形状（如图），当白珠子比黑珠子多10颗时，一共用了多少颗白珠子？【解析】将两排作为一组，可以发现每组白珠就比黑珠多1颗，现在白珠共比黑珠多10颗，说明有10组，那么共有20排，双数排是白珠，一共用了2＋4＋6＋8＋……＋18＋20＝110（颗）.解答：当白珠子比黑珠子多10颗时，一共用了110颗白珠子.将同学们编为两组，做脑筋急转弯的游戏，一组出题，另一组回答，轮流进行.同学们有很多这样的题目，谨举两例，抛砖引玉.什么话可以世界通用?【脑筋急转弯答案：电话】数字0到1之间加一个什么号，才能使这个数比0大，而比1小呢？答案：加个“.”成为“0.1”【脑筋急转弯答案：加个“.”成为“0.1”】这种训练，对数学审题和逻辑思维能力的培养非常有效.。

第四讲等差数列（下）1、巩固等差数列中求解和、项数、公差的公式，复习前一讲内容；2、学会应用等差数列求解生活中的问题；3、培养学生数感，激发学生对数学的兴趣，提高学员数学学习的自信。

掌握等差数列中公差、首项、末项、项数等各个名词代表的意义，以及计算的公式和方法：（1）通项公式中更注重n ma a n m d-=-⨯（）的应用。

（2）项数公式11nn a a d=-÷+（）始终贯穿整个等差数列的专题。

（3）求和公式：和＝(首项＋末项)×项数÷2（4）注意中项定理在题目中的运用，找出需要的数量关系。

在本讲中除了巩固如上内容，添加1＋2＋3＋……＋（n－1）＋n＋（n－1）＋……＋3＋2＋1＝n²在等差数列解题中的应用。

兔读一本书，第一天读30页，从第二天起，每天读的页数都必须比前一天多4页，最后一天读了70页刚好读完，这本书共有几页？【解析】先求小红看了几天，（70－30）÷4＋1＝11天，再求这本书总页数：（30＋70）×11÷2＝550页。

解答：这本书共有550页。

计算：1＋2＋3＋……＋19＋20＋19＋……＋3＋2＋1【解析】方法一：分两个等差数列求和计算，（1＋20）×20÷2＋（19＋1）×19÷2＝400。

方法二：1＋2＋3＋……＋(n-1)＋n ＋(n-1)＋……＋3＋2＋1＝n ²，20×20＝400。

解答：1＋2＋3＋……＋19＋20＋19＋……＋3＋2＋1＝400。

把210拆成7个自然数的和，使这7个数从小到大排成一行后，相邻两个数的差都是5，那么，第1个数与第6个数分别是多少？【解析】由题可知：由210拆成的7个数一定构成等差数列，则中间一个数为210÷7＝30，所以，这7个讲演者：得分：讲演者：得分：数分别是15，20，25，30，35，40，45。

奥数思维训练题库---计算【分组】【2】计算：1－2＋3－4＋5－……－1994＋1995=【答案】998【分组】【2】计算：1－2＋3－4＋5－……－2014＋2015=【答案】1008【分组】【2】计算：（2＋4＋6＋…＋1996）－（1＋3＋5＋…＋1995）=【答案】998【分组】【2】计算：（2＋4＋6＋…＋2014）－（1＋3＋5＋…＋2013）=【答案】1007【分组】【2】3－5+7－9+11－13+…+2011－2013+2015=【答案】1009【提取公因数】【2】计算：222＋333＋444＋555＋666=【答案】2220444×5=2220【提取公因数】【2】计算：111＋222＋333＋444＋555＋666=【答案】2331【位值原理】【2】（123456＋234561＋345612＋456123＋561234＋612345）÷111111= 【答案】21【提取公因数】【2】计算：1÷2015+2÷2015+3÷2015+…+2014 ÷2015+2015÷2015= 【答案】1008【提取公因数】【乘法凑整】【2】计算：3.6×31.4＋(31.4＋12.5)×6.4=【答案】394【提取公因数】【乘法凑整】【2】计算：3.6×30.4＋(30.4＋12.5)×6.4=【答案】384【提取公因数】【分拆】【3】计算：161.8×6.18＋2618×0.382=【答案】2000【提取公因数】【3】计算：(4.16×84－2.08×54－0.15×832)÷0.32【答案】1248【分拆】【凑整】【2】计算:0.75＋9.75＋99.75＋999.75＋1=【答案】1111【分拆】【提取公因数】【3】7210810846(118142118134)⨯+⨯-⨯-⨯【答案】11800【提取公因数】【2】计算：0.9999×0.7+0.1111×2.7=【答案】0.9999【提取公因数】【2】1994.5×81+0.24×800+2.4+8.1×31=【答案】162000【凑整】【1】计算：98＋998＋9998＋99998=【答案】111092【凑整】【1】计算：8＋998＋9998＋99998=【答案】111002【提取公因数】【凑整】【2】计算：（8.88+8.88+8.88+8.88）×1.25= 【答案】44.4【提取公因数】【2】20.14×37－201.4×1.9＋2.014×820=【答案】2014【提取公因数】【2】计算：17.48×37－174.8×1.9＋1.748×820=【答案】1748【提取公因数】【2】计算：2098－5.5×7.5－0.25×55－45=【答案】19982098－5.5×7.5－0.25×55－45=2098－55×(0.75＋0.25)－45=2098－(55＋45)=1998【提取公因数】【2】8.1×1.3－8÷1.3+1.9×1.3+11.9÷1.3=【答案】10【提取公因数】【2】999.99×222.22+333.33×333.34 =【答案】333330【提取公因数】【2】51.2×32.5+512×6.74+5.12=【答案】5120【分拆】【2】325.24+425.24+625.24+925.24+525.24=【答案】2826.2【分拆】【提取公因数】【3】计算：333×332332333－332×333333332【答案】665【分拆】【重码数】【3】19501950×2010－20112011×1949=【答案】61061【提取公因数】【2】计算：9.99×0.13－0.111×2.7【答案】0.999【定义新运算】【3】对于任意两个自然数A 和B 、规定一种新运算“※”：A ※B=A （A ＋1）（A ＋2）……（A ＋B －1）。

六年级下册数学思维提升—易错难点训练及答案含详细答案一、培优题易错题1．如图，用相同的小正方形按照某种规律进行摆放，则第6个图形中小正方形的个数是________，第n（n为正整数）个图形中小正方形的个数是________（用含n的代数式表示）．【答案】55；（n+1）2+n【解析】【解答】第1个图形共有小正方形的个数为2×2+1；第2个图形共有小正方形的个数为3×3+2；第3个图形共有小正方形的个数为4×4+3；…；则第n个图形共有小正方形的个数为（n+1）2+n，所以第6个图形共有小正方形的个数为：7×7+6=55．故答案为：55；（n+1）2+n【分析】观察图形规律，第1个图形共有小正方形的个数为2×2+1；第2个图形共有小正方形的个数为3×3+2；则第n个图形共有小正方形的个数为（n+1）2+n，找出一般规律.2．如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走均为正，向下向左走均为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向．（1）图中A→C（________，________），B→C（________，________），C→________（+1，﹣2）；（2）若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置；（3）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程．（4）若图中另有两个格点M、N，且M→A（3﹣a，b﹣4），M→N（5﹣a，b﹣2），则N→A应记为什么？【答案】（1）+3；+4；+2；0；D（2）解：P点位置如图1所示；（3）解：如图2，根据已知条件可知：A→B表示为：（1，4），B→C记为（2，0）C→D记为（1，﹣2）；则该甲虫走过的路线长为：1+4+2+1+2=10（4）解：由M→A（3﹣a，b﹣4），M→N（5﹣a，b﹣2），所以，5﹣a﹣（3﹣a）=2，b﹣2﹣（b﹣4）=2，所以，点A向右走2个格点，向上走2个格点到点N，所以，N→A应记为（﹣2，﹣2）【解析】【解答】解：（1）图中A→C（+3，+4），B→C（+2，0），C→D（+1，﹣2）；故答案为：（+3，+4），（+2，0），D；【分析】（1）根据向上向右走均为正，向下向左走均为负确定数据即可；（2）根据所给的路线确定点的位置即可；（3）根据表示的路线确定长度相加可得结果；（4）观察点的变化情况，根据（1）即可确定点走了格数，从而确定结论.3．某手机经销商购进甲，乙两种品牌手机共 100 部.（1）已知甲种手机每部进价1500 元，售价2000 元；乙种手机每部进价3500 元，售价4500 元；采购这两种手机恰好用了 27 万元 .把这两种手机全部售完后，经销商共获利多少元？（2）已经购进甲，乙两种手机各一部共用了5000 元，经销商把甲种手机加价50%作为标价，乙种手机加价 40%作为标价.从 A，B 两种中任选一题作答：A：在实际出售时，若同时购买甲，乙手机各一部打九折销售，此时经销商可获利1570 元.求甲，乙两种手机每部的进价.B：经销商采购甲种手机的数量是乙种手机数量的 1.5 倍.由于性能良好，因此在按标价进行销售的情况下，乙种手机很快售完，接着甲种手机的最后10 部按标价的八折全部售完.在这次销售中，经销商获得的利润率为 42.5%.求甲，乙两种手机每部的进价.【答案】（1）解：设购进甲种手机部，乙种手机部，根据题意，得解得：元.答：销商共获利元.（2）解：A: 设每部甲种手机的进价为元，每部乙种手机的进价元，根据题意，得解得：答：求甲，乙两种手机每部的进价分别为：3000元，2000元.B:乙种手机：部，甲种手机部，设每部甲种手机的进价为元，每部乙种手机的进价元，根据题意，得解得：答：求甲，乙两种手机每部的进价分别为：2000元，3000元.【解析】【分析】（1）甲的单价乘以部数加上乙的单价乘以部数等于总数，根据题意列出，然后解方程得到结果。

六年级下册数学试题-思维能力训练试卷（1）（无答案）全国通用六年级数学思维能力训练试卷（第1套）(总分100分时间90分钟)题号一二合计得分一、填空题（本大题共15小题，每小题3分，共45分）1．在NBA总决赛的一场比赛中，骑士球星詹姆期全场27投16中加上8罚6中，得41分，已知3分线外投中一球记3分，3分线内投中一球算2分，罚球算1分，则詹姆期本场比赛投中了个3分球。

2．一根粗细均匀的竹竿（长约1米），在中点的位置打个小孔并拴上绳子．左边的塑料袋在刻度4上，放3个棋子，右边的塑料袋在刻度3上，放个棋子才能保持平衡。

3．蜡烛每分钟燃烧的长度一定，一支蜡烛点火8分钟后长12厘米，点火18分钟后长7厘米，这支蜡烛点火分钟的长度是1厘米。

4．有一个空罐如右图，如果倒人6碗浓果汁和3杯水，刚好倒满；如果倒入2碗浓果汁和2杯水，液面到达A处。

那么，要想倒到这个空罐的一半需要碗浓果汁或者杯水。

5．一个等腰三角形底和高的比是8：3，如果沿着它的高剪开后，拼成一个长方形，这个长方形的面积是192平方厘米，然后再把拼成的长方形卷成一个最大的圆柱，这个圆柱的体积立方厘米（π=3）。

6．A是大于0小于10的自然数，B是0，用字母A、B组成一个能同时被2、3、5整除的四位数是7．计算机是将信息转化成二进制数进行处理的，二进制“逢二进一”，(1101)2表示二进制数，将它转化成十进制形式是1´23+1´22+0´21+1´20=13，那么将二进制数(11011)2转化成十进制形式是数8．何师傅将一批博易新思维教材装箱，当他装满15箱时，发现已装的书比这批书的4还少24本，接着他又装满13箱，正好装完。

这批书共有本。

79．一个盒子里有黑、白、红三色的珠子共17颗，其中白色珠子的颗数是红色珠子的7倍，那么盒子里最少有颗黑珠子。

10．如图：某公园的外轮廓是四边形，被对角线AC、BD分成四个部分，三角形AOD的面积是1平方千米，三角形BOC的面积是2平方千米，三角形COD的面积2是3平方千米，公园人工湖的面积是3千米。

六年级数学下册思维训练五
例1、一个圆锥体的容器，高15厘米，底面半径比高少7厘米，容器装满水后全部倒入一个长20厘米，宽10厘米，高6厘米的长方体容器中，这时水面距离长方体容器口多少厘米？
例2、如下图，有一张长16.56分米的长方形铁皮，现在把它剪成两个圆和一个长方形并做成一个圆柱，求这个圆柱的表面积？
例3、一个皮箱的形状如下图，横截面是一个直角梯形，上底15厘米，下底25厘米，高40厘米。

皮箱的长是5分米、求出它的体积约为多少立方分米？
例4、一个圆柱形的玻璃杯中盛有水，水面高2.5厘米，玻璃杯内侧的底面积是72平方厘米，在这个杯中放进棱长6厘米的正方体铁块后，水面没有淹没铁块，这时水面高多少厘米？
练习1、一个圆柱形的水桶，放进一根底面半径是5厘米的圆钢，把圆钢完全放入水中，水面上升9厘米，这时如果把水中的圆钢往上提，使它露出水面8厘米，那么这时水桶的水就会下降4厘米。

求圆钢的体积。

练习2、一个长方体的容器中有一些水，水面高是5厘米，容器底面积是52 平方厘米（不计厚度），现在放入一个底面半径是3厘米的圆柱体，水面没有淹没圆柱体，这时水面高是多少厘米？（圆周率取3）。

六年级数学思维训练题11、两个相同的瓶子装满酒精溶液。

一个瓶中酒精与水的比2︰3，另一个瓶中酒精与水的比是3︰5，若把两瓶酒精溶液混合，混合后酒精与水的比是多少？分析与解答：因为两个瓶子相同，可以分别求出每个瓶中酒精占瓶子容积的几分之几，在求出混合后酒精和水各占容器容积的几分之几，即可求出混合后酒精与水的比。

2、某饮料店有一桶奶茶，上午售出其中的25%，下午售出30升，晚上售出剩下的10%，最后剩下的奶茶再减6升刚好半桶，问一桶奶茶共有多少升？【考点】L6：分数和百分数应用题【分析】设一桶奶茶共有a升，则晚上售出（a﹣25%a﹣30）×10%，此时剩下（a﹣25%a﹣30）×（1﹣10%），对应着50%a+6，列出方程求解。

【解答】解：设一桶奶茶共有a升（a﹣25%a﹣30）×（1﹣10%）＝50%a+6（0.75a﹣30）×0.9＝0.5a+60.675a﹣27＝0.5a+60.175a＝333、学校里买来了5个保温瓶和10个茶杯，共用了90元钱。

每个保温瓶是每个茶杯价钱的4倍，每个保温瓶和每个茶杯各多少元?分析与解:根据每个保温瓶的价钱是每个茶杯的4倍，可把5个保温瓶的价钱转化为20个茶杯的价钱。

这样就可把5个保温瓶和10个茶杯共用的90元钱，看作30个茶杯共用的钱数。

解:每个茶杯的价钱:90÷(4×5+10)＝3(元)每个保温瓶的价钱3×4＝12(元)答:每个保温瓶12元，每个茶杯3元。

4、某工地运进一批沙子和水泥，运进沙子袋数是水泥的2倍。

每天用去30袋水泥，40袋沙子，几天以后，水泥全部用完，而沙子还剩120袋，这批沙子和水泥各多少袋?分析与解:由己知条件可知道，每天用去30袋水混，同时用去30×2袋沙子才能同时用完。

但现在每天只用去40袋沙子，少用(30×2-40)袋，这样オ累计出120袋沙子。