3.含容电路的分析与计算方法

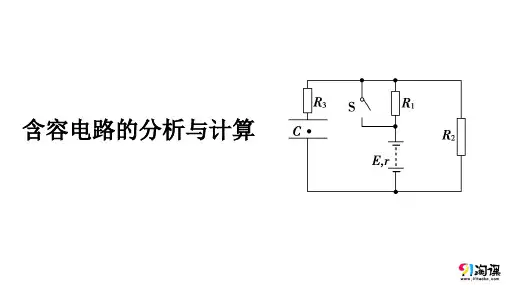
含容电路和电路故障分析一、含电容电器的分析与计算方法在直流电路中，当电容器充、放电时，电路里有充、放电电流.一旦电路达到稳定状态，电容器在电路中就相当于一个阻值无限大（只考虑电容器是理想的不漏电的情况）的元件，在电容器处电路可看作是断路，简化电路时可去掉它.简化后若要求电容器所带电量时，可接在相应的位置上.分析和计算含有电容器的直流电路时，需注意以下几点：（1）电路稳定后，由于电容器所在支路无电流通过，所以在此支路中的电阻上无电压降，因此电容器两极间的电压就等于该支路两端的电压.（2）当电容器和电阻并联后接入电路时，电容器两极间的电压与其并联电阻两端的电压相等.（3）电路的电流、电压变化时，将会引起电容器的充（放）电.如果电容器两端电压升高，电容器将充电；如果电压降低，电容器将通过与它连接的电路放电.【例1】如图所示，电源电动势E ＝12V ，内阻r ＝1Ω，电阻R 1＝3Ω，R 2＝2Ω，R 3＝5Ω，电容器的电容C 1＝4μF ，C 2＝1μF 。

求:(1)当S 闭合时间足够长时，C 1和C 2所带的电量各是多少?(2)然后把S 断开，S 断开后通过R 2的电量是多少?解:(1)当S 闭合时间足够长时，C 1两端的电压等于R 2两端的电压；C 2两端的电压等于路端电压 回路电流122E I A r R R ==++ C 1两端的电压U C1＝U 2＝IR 2＝4VC 1的带电量为：Q 1＝C 1U C1＝4×10－6×4C ＝1.6×10－5CC 2两端的电压U C2＝U ＝I （R 1＋R 2）＝10VC 2的带电量为：Q 2＝C 2U C2＝1×10－6×10C ＝1.0×10－5C（2）断开S 后，电容器C 1通过电阻R 2、R 3放电；电容器C 2通过电阻R 1、R 2、R 3放电，放电电流均流过R 2，且方向相同。

因此，通过R 2的电量为:Q ＝Q 1＋Q 2＝1.6×10－5C ＋1.0×10－5C ＝2.6×10－5C【例2】如图，已知源电动势E ＝12V ，内电阻不计。

电容的运算放大器电路是一种常见的电子电路，它可以实现电压放大和滤波功能，广泛应用于许多电子系统中。

本文将从基本概念、电路结构、工作原理和计算方法等方面对含电容的运算放大器电路进行详细介绍，帮助读者更好地理解和应用这一电路。

一、基本概念1. 运算放大器（Operational Amplifier，简称Op-Amp）是一种集成电路，具有高增益、高输入阻抗、低输出阻抗等特点，广泛应用于电子电路中。

2. 电容是一种存储电荷的元件，具有阻抗与频率成反比的特性，可以用于滤波和信号处理。

二、电路结构含电容的运算放大器电路通常由运算放大器、电容和其它元件组成，其中电容可以用来实现滤波、积分、微分等功能。

三、工作原理1. 电容的作用：电容在运算放大器电路中可以用来滤波、积分、微分等。

在滤波电路中，电容可以与电阻配合，实现低通滤波、高通滤波、带通滤波等功能。

2. 电容的阻抗特性：电容的阻抗与频率成反比，即Zc=1/(jωC)，其中Zc为电容的阻抗，ω为角频率，C为电容的电容值。

3. 运算放大器的特性：运算放大器具有高输入阻抗、低输出阻抗、无限大的开环增益等特点，在实际应用中可以近似认为是理想运算放大器。

四、计算方法1. 低通滤波电路的计算：对于低通滤波电路，可以通过电容和电阻的组合来实现。

其传递函数为H(jω)=1/(1+jωR1C1)，其中R1和C1分别为电阻和电容的取值。

通过调整R1和C1的取值，可以实现不同的频率特性。

2. 高通滤波电路的计算：高通滤波电路同样可以通过电容和电阻的组合来实现。

其传递函数为H(jω)=jωR2C2/(1+jωR2C2)，其中R2和C2分别为电阻和电容的取值。

通过调整R2和C2的取值，可以实现不同的频率特性。

3. 带通滤波电路的计算：带通滤波电路通常采用多级滤波电路进行实现，可以组合低通滤波和高通滤波电路来实现。

可以通过串联或并联的方式组合低通和高通滤波电路，来实现不同的频率特性。

专题20 含容电路的分析及计算一：专题概述解决含电容器的直流电路问题的一般方法：（1) 不分析电容器的充、放电过程时,把电容器处的电路视为断路,简化电路时可以去掉，求电荷量时再在相应位置补上。

（2）电路稳定后，与电容器串联的电路中没有电流,同支路的电阻相当于导线，即电阻不起降压的作用,但电容器两端可能出现电势差.(3）电路中电流、电压的变化可能会引起电容器的充、放电。

若电容器两端电压升高,电容器将充电；若电压降低,电容器将通过与它连接的电路放电.(4）如果电容器与电源并联，且电路中有电流通过,则电容器两端的电压不是电源电动势E,而是路端电压U.(5) 如果变化前后极板带电的电性相同,那么通过每根引线的电荷量等于始、末状态电容器带电荷量之差；如果变化前后极板带电的电性改变,那么通过每根引线的电荷量等于始、末状态电容器带电荷量之和.二：典例精讲1．电容器与滑动变阻器的电路分析典例1：在如图所示的电路中，闭合电键S，将滑动变阻器滑片P向a端移动一段距离,下列结论正确的是A．灯泡L变亮B．电流表读数变大C．电容器C上的电荷量增多D．电压表读数变小【答案】C2．电容与传感器结合的电路分析典例2：如图所示的电路中，R1、R2、R3是固定电阻，R4是光敏电阻，其阻值随光照强度的增强而减小。

当开关S闭合且没有光照射时，电容器C不带电。

当用强光照射R4且电路稳定时，则与无光照射时比较A．电容器C的上极板带正电B．电容器C的下极板带正电C．通过R4的电流变小，电源的路端电压增大D．通过R4的电流变大,电源提供的总功率变小【答案】B3．电容器与二极管电路的分析典例3：如图所示的电路中,电源电动势E=6V，内阻r=1Ω，电阻R1=3Ω,R2=6Ω，电容器的电容C=3。

6μF，二极管D具有单向导电性。

开始时，开关S1闭合,S2断开.(1）合上S2,待电路稳定以后，求电容器上电荷量变化了多少.(2）合上S2，待电路稳定以后再断开S1,求断开S1后流过R1的电荷量是多少.【答案】（1) 减少1.8×10—6C(2) 9.6×10—6C【解析】（1) 设开关S1闭合，S2断开时，电容器两端的电压为U1,干路电流为I1，根据闭合电路欧姆定律有I1==1。

含电容器电路的分析与计算电容器是一种重要的电子元件，广泛应用于电路中。

在电容器电路的分析与计算中，我们需要了解电容器的基本原理、参数和特性，以及如何计算电容器电路中的电压、电流和时间常数等。

首先，电容器是一种能够储存电荷的电子元件，由两个导体板和介质组成。

常用的电容器有金属箔电容器、陶瓷电容器和电解电容器等，其容值单位是法拉(F)。

电容器的容量取决于其两个导体板之间的面积、板间的距离和介质的电容常数。

在电容器电路中，电容器的两个导体板分别连接到电路的两个节点，形成一个开回路。

当电容器充电时，电容器两个板之间的电荷会积累，并且在两个板之间形成一个电势差。

根据库仑定律，电容器的电压与其所储存的电荷量成正比。

电容器的电压-电荷关系可以表示为V=Q/C，其中V 是电容器的电压，Q是电容器所储存的电荷量，C是电容器的容值。

在电容器电路中，常用于分析和计算的是RC电路和RLC电路。

1.RC电路：RC电路由电阻和电容器组成，常用于滤波和积分电路。

在RC电路中，电容器会充电和放电，形成一个充放电过程。

当电容器充电时，电流通过电阻，电压逐渐上升。

当电容器放电时，电流从电容器流向电阻，电压逐渐下降。

在RC电路中，电容器的充放电过程遵循指数衰减的规律，其电压变化可以用指数函数来描述。

2.RLC电路：RLC电路由电感、电阻和电容器组成，常用于振荡、滤波和谐振电路。

在RLC电路中，电容器和电感可以形成共振回路，当外部输入信号频率等于回路共振频率时，电流最大。

RLC电路的分析和计算可利用电压-电流关系和频率响应等进行求解。

在电容器电路分析和计算时，我们可以通过以下步骤进行：1.确定电容器电路的拓扑结构：确定电容器的连接方式、电阻和电感的位置等。

2.建立电容器电路的数学模型：通过电压和电流的关系、电容器的电压-电荷关系等，建立电容器电路的数学方程。

3.求解电容器电路的初始条件：根据电路的初始状态，确定初始电荷量、电压和电流。

含电容器直流电路的分析与计算问题摘要：初次接触电路问题的中学生在利用欧姆定律和串、并联电路的特点进行定性分析和定量计算时，往往觉得很”繁”、很”乱”、很”难”。

其实，解决电路问题的关键在于掌握思路和方法：一般是先对电路进行变形、整理，组成简单的串、并联电路，然后利用欧姆定律及串联的特点建立方程。

学生的问题大多不是出在电路分析阶段，而是建立方程阶段。

关键词：含电容器，直流电路；分析，计算中图分类号：g633.7 文献标识码：e 文章编号：1006-5962（2013）01-0194-01电学是中学物理的重点，也是难点。

欧姆定律又是电学的基础。

初次接触电路问题的中学生在利用欧姆定律和串、并联电路的特点进行定性分析和定量计算时，往往觉得很”繁”、很”乱”、很”难”。

其实，解决电路问题的关键在于掌握思路和方法：一般是先对电路进行变形、整理，组成简单的串、并联电路，然后利用欧姆定律及串联的特点建立方程。

学生的问题大多不是出在电路分析阶段，而是建立方程阶段，在教学中，发现学生”乱”就乱在不知先用哪个公式算什么量.后用哪个公式算什么量。

往往花很长时间还理不出头绪，于是，越想越糊涂，简单的问题也变难了，当然解决不了，怎么办呢？很简单，只要有一种能迅速获得计算结果的方法就行了。

本文以两个用电器串、并联电路为例，介绍一种简单快捷的电器计算方法。

直流电路中，当电容器充放电时，电路里有充、放电电流。

一旦电路达到稳定状态，电容器在电路中就相当于一个阻值无限大（只考虑电容器是理想的不漏电情况）的元件，电容器所在支路可视为断路，简化电路时可去掉，简化后若要求电容器所带电荷量，可接在相应的位置。

【例1】如图1所示，两个电阻r1=5ω，r2=10ω，两电容器c1=5μf，c2=10μf，电路两端电压恒定，u=18v，求：（1）当s断开时，a、b两点间的电压为多大？（2）当s闭合时，两电容器的带电量分别改变了多少？【解析】（1）直流电不能通过c1、c2，所以当s断开时，电路中无电流。

含容电路动态分析一、技巧1．含电容器的电路的分析和计算，要抓住电路稳定时电容器相当于断路.分析稳定状态的含容电路时可先把含有电容器的支路拆除，画出剩下电路等效电路图，之后把电容器接在相应位置。

2．如果变化前后极板带电的电性相同，那么通过每根引线的电荷量等于始末状态电容器电荷量的差；如果变化前后极板带电的电性改变，那么通过每根引线的电荷量等于始末状态电容器电荷量之和。

二、例题[例题1] 如下图所示，U=10V，电阻R1=3Ω，R2=2Ω，R3=5Ω，电容器的电容C1=4μF，C2=1μF，求：（1）若电路稳定后，C1、C2的带电量？（2）S断开以后通过R2的电量及R2中电流的方向？例题2：如图所示电路中，电源电动势E＝10v，内电阻不计，电阻R1＝14Ω，R2＝6.0Ω，R3＝2.0Ω，R4＝8.0Ω，R5＝10Ω，电容器的电容C＝2μF，求：（1）电容器所带的电荷量Q。

并说明电容器哪个极板带正电．（2）若R2突然断路，将有多少电荷量ΔQ通过R5？例题3．如图所示的电路中，在A、B两点间接一电动势为4V，内电阻为1Ω的直流电源，电阻R1=R2=R=4Ω，电容器C的电容为30μF，电流表的内阻不计，求：三、习题1.如图所示，电源电动势E＝10 V，内阻r＝1 Ω，R1＝3 Ω，R2＝6 Ω，C＝30 μF.，当闭合开关S，求（1）稳定后电容器所带的电量Q=？（2）开关S断开后通过R1的电荷量ΔQ=？2．在如图所示的电路中，电源电动势E=9V, R1=11Ω，r=1Ω，R2=R3=6Ω，当开关S闭合且电路稳定时，电容器C的带电荷量为Q1；当开关S断开且电路稳定时，电容器C的带电量为Q2，求Q1，Q2为多少库伦？开关S由闭合到断开后通过R1的电荷量ΔQ=？3．如图所示，已知电源电动势E=12V,内电阻r=1Ω，R1=3 Ω，R2=2Ω，R3=5Ω，C1=4µF， C2 =1µF ,求：（1）电键S闭合后，C1，C2所带电量？（2）电键S断开后通R2过的电量为多少？4．如图所示的电路中，已知电容C1=C2，电阻R1﹥R2，电源内阻可忽略不计，当开关S接通时，以下说法中正确的有（）A.C1的电量增多，C2的电量减少B.C1的电量减少，C2的电量增多C.C1、C2的电量都减少D.C1、C2的电量都增多5.如图所示的电路中，E＝10 V，R1＝4 Ω，R2＝6 Ω，电池内阻不计，C1＝C2＝30 μF.先闭合开关S，待电路稳定后再断开S，求断开S后通过电阻R1的电荷量.6.如图所示电路中R1=R2=R3=8Ω，电容器电容C=5 F，电源电动势E=6V，内阻不计，求电键S由稳定的闭合状态断开后流过R3的电荷量．7.如图所示电路，电源电动势E=12V，内阻r=1Ω。

习题课：含容电路分析和计算——凯里一中：杨昌芬[典例1]电路中E ＝10 V ，R 1＝4 Ω，R 2＝6 Ω，C ＝30 μF.电池内阻可忽略．(1)闭合开关S ，求稳定后通过R 1的电流；(2)然后将开关S 断开，求这以后通过R 1的总电量．[解析] (1)电路稳定后，电容器所在的支路上无电流通过，因此R 1与R 2串联，C 两端的电压即为R 2两端的电压．由欧姆定律得通过R 1的电流I ＝E R 1＋R 2＝104＋6A ＝1 A. (2)S 断开前，C 两端电压U 1＝IR 2＝6 VC 所带电量Q 1＝CU 1＝30×10－6×6 C ＝1.8×10－4 C开关S 断开稳定后，总电流为零，电容器两端电压为E ，所带电量Q 2＝CE ＝30×10－6×10C ＝3×10－4 C通过R 1的电量，即为电容器增加的电量[答案] (1)1 A (2)1.2×10－4C [典例2]、如图所示的电路中，R 1＝R 2＝R 3＝8 Ω，C ＝5 μF ，E ＝6 V 内阻不计，求开关S 由稳定闭合状态断开后流过R 3 的电荷量？[解析] (1)电路稳定后，电容器所在的支路上无电流通过，因此R 1与R 2串联，C 两端的电压即为R 2两端的电压．由欧姆定律得通过R 1的电流I ＝E R 1＋R 2＝3／8 A. (2)S 断开前，C 两端电压U 1＝IR 2＝3 VC 所带电量Q 1＝CU 1＝5×10－6×3C ＝1.5×10－5 C开关S 断开稳定后，总电流为零，电容器两端电压为R 1两端的电压U 1，所带电量Q 2＝CU 1＝5×10－6×3C ＝1.5×10－5 C通过R 1的电量，即为电容器增加的电量ΔQ ＝Q 2+Q 1＝3×10－5 C.[典例３].如图所示，已知C ＝6 μF ，R1＝5 Ω，R 2＝6 Ω，E ＝6 V ，r ＝1 Ω，电表均为理想电表，开关S 原来处于断开状态，下列说法中正确的是( )A ．开关S 闭合瞬间，电流表的读数为0.5 AB ．开关S 闭合瞬间，电压表的读数为5.5 VC ．开关S 闭合后经过一段时间，再将开关S 迅速断开，则通过R 2的电荷量为1.8×10－5 CD ．以上说法都不对[解析] 开关S 闭合瞬间，电容器充电，接近于短路状态，I ＝E R 1＋r ＝65＋1A ＝1 A ，A 错误；电压表的读数U ＝IR 1＝1×5 V ＝5 V ，B 错误；开关闭合一段时间后，电容器相当于断路，I ′＝E R 1＋R 2＋r ＝65＋6＋1A ＝0.5 A ，此时电容器上电荷量Q ＝CU 2＝CI ′R 2＝6×10－6×0.5×6 C ＝1.8×10－5C ，断开开关S 后，电荷量Q 经R 2释放，故C 正确．解决含电容器的直流电路问题的一般方法：(1)通过初末两个稳定的状态来了解中间不稳定的变化过程。

含容电路分析计算技巧和实例电容器是一个储存电能的元件．在直流电路中，当电容器充放电时，电路里有充放电电流，一旦电路达到稳定状态，电容器在电路中就相当于一个阻值无限大（只考虑电容器是理想的不漏电的情况）的元件，在电容器处电路看作是断路，简化电路时可去掉它。

简化后若要求电容器所带电荷量时，可在相应的位置补上。

分析和计算含有电容器的直流电路时，需注意以下几点：(1)电路稳定后，由于电容器所在支路无电流通过．所以在此支路中的电阻上无电压降，因此电容器两极间的电压就等于该支路两端的电压．(2)当电容器和用电器并联后接入电路时，电容器两极间的电压与其并联用电器两端的电压相等．(3)电路的电流、电压变化时,将会引起电容器的充(放)电．如果电容器两端电压升高,电容器将充电,如果电压降低，电容器将通过与它并联的电路放电.电容器两根引线上的电流方向总是相同的，所以要根据正极板电荷变化情况来判断电流方向。

⑷如果变化前后极板带电的电性相同，那么通过每根引线的电荷量等于始末状态电容器电荷量的差；如果变化前后极板带电的电性改变，那么通过每根引线的电荷量等于始末状态电容器电荷量之和。

含有电容器的电路解题方法（1）先将含电容器的支路去掉（包括与它串在同一支路上的电阻），计算各部分的电流、电压值。

（2）电容器两极扳的电压，等于它所在支路两端点的电压。

（3）通过电容器的电压和电容可求出电容器充电电量。

（4）通过电容器的电压和平行板间距离可求出两扳间电场强度，再分析电场中带电粒子的运动。

例1：如图所示的电路，水平放置的平行板电容器中有一个带电液滴正好处于静止状态，现将滑动变阻器的滑片P向左移动，则（）A．电容器中的电场强度将增大B．电容器上的电荷量将减少C．电容器的电容将减小D．液滴将向上运动由题意可知，电容器与R2并联，根据闭合电路欧姆定律可确定随着滑片左移，电阻的变化，导致电压的变化，从而判定电阻R2的电压变化，再根据可得，电容器的电量及由E=知两极间的电场强度如何变化．【解析】A、电容器两板间电压等于R2两端电压．当滑片P向左移动时，R2两端电压U 减小，由E=知电容器中场强变小，A错误；B、根据可得，电容器放电，电荷量减少，B项正确；C、电容器的电容与U的变化无关，保持不变，C项错误．D、带电液滴所受电场力变小，使液滴向下运动，D项错误；故选：B例2：在如图所示的电路中，电源两端A、B 间的电压恒定不变，开始时S断开，电容器上充有电荷．闭合S后，以下判断正确的是（）A．C1所带电量增大，C2所带电量减小B．C1所带电量减小，C2所带电量增大C．C1、C2所带电量均减小D．C1、C2所带电量均增大S断开时，外电路中没有电流，两电容器的电压都等于电源的电动势，S闭合后，两电容器的电压都小于电源的电动势，根据Q=CU分析电容器电量的变化．【解析】S断开时，外电路中没有电流，两电容器的电压都等于电源的电动势．S闭合后，两电阻串联，电容器C1的电压等于R1的电压，电容器C2的电压等于R2的电压，可知两电容器的电压都小于电源的电动势，根据Q=CU分析可知两电容器电量均减小．故C正确，ABD错误．故选C例3：如图所示的电路中，R1、R2、R3是固定电阻，R4是光敏电阻，其阻值随光照的强度增强而减小．当开关S闭合且没有光照射时，电容器C不带电．当用强光照射R4且电路稳定时，则与无光照射时比较（）A．电容器C的上极板带正电B．电容器C的下极板带正电C．通过R4的电流变小，电源的路端电压增大D．通过R4的电流变大，电源提供的总功率变小电容在电路稳定时可看作开路，故由图可知，R1、R2串联后与R3、R4并联，当有光照射时，光敏电阻的阻值减小，由闭合电路欧姆定律可得出电路中总电流的变化及路端电压的变化，再分析外电路即可得出C两端电势的变化，从而得出电容器极板带电情况；同理也可得出各电阻上电流的变化．【解析】因有光照射时，光敏电阻的阻值减小，故总电阻减小；由闭合电路的欧姆定律可知，干路电路中电流增大，由E=U+Ir可知路端电压减小；R1与R2支路中电阻不变，故该支路中的电流减小；则由并联电路的电流规律可知，另一支路中电流增大，即通过R2的电流减小，而通过R4的电流增大，故C、D错误；当没有光照时，C不带电说明C所接两点电势相等，以电源正极为参考点，R1上的分压减小，而R3上的分压增大，故上极板所接处的电势低于下极板的电势，故下极板带正电；故A错误，B正确；故选B．例4:如图所示的电路中，两平行金属板A、B水平放置，极板长L=80cm，两板间的距离d=40cm．电源电动势E=40V，内电阻r=1Ω，电阻R=15Ω，闭合开关S，待电路稳定后，将一带负电的小球从B板左端且非常靠近B板的位置以初速度v=4m/s水平向右射入两板高效课堂—实验微专题间，该小球可视为质点．若小球带电量q=1×10-2C，质量为m=2×10-2kg，不考虑空气阻力，电路中电压表、电流表均是理想电表．若小球恰好从A板右边缘射出（g取10m/s2）．求：（1）滑动变阻器接入电路的阻值为多少？（2）此时电流表、电压表的示数分别为多少？（3）此时电源的输出功率是多少？（1）小球进入电场中做类平抛运动，小球恰好从A板右边缘射出时，水平位移为L，竖直位移为d，根据运动学和牛顿第二定律结合可求出板间电压，再根据串联电路分压特点，求解滑动变阻器接入电路的阻值．（2）根据闭合电路欧姆定律求解电路中电流，由欧姆定律求解路端电压，即可求得两电表的读数．（3）电源的输出功率P=UI，U是路端电压，I是总电流．【解析】（1）小球进入电场中做类平抛运动，水平方向做匀速直线运动，竖直方向做匀加速运动，则有：水平方向：L=vt竖直方向：d=由上两式得：a===20m/s2又根据牛顿第二定律得：a=联立得：U==V=24V根据串联电路的特点有：=代入得：=解得，滑动变阻器接入电路的阻值为R′=24Ω（2）根据闭合电路欧姆定律得电流表的示数为：I==A=1A电压表的示数为：U=E-Ir=（40-1×1）V=39V（3）此时电源的输出功率是P=UI=39×1W=39W．答：（1）滑动变阻器接入电路的阻值为24Ω．（2）此时电流表、电压表的示数分别为1A和39V．（3）此时电源的输出功率是39W．每日一练解析C为板间距离固定的电容器，电路连接如图所示，当滑动触头P向右缓慢滑动的过程中，下列说法中正确的是（）A．电容器C充电B．电容器C放电C．流过电流计G的电流方向为a→G→bD．流过电流计G的电流方向为b→G→a首先明确含电容器的支路等效为断路，且两端的电压为并联部分的电压相等；当滑动触头P向右缓慢滑动的过程中，该电路的总电阻不变，但与电容器并联部分的电阻减少，即电容器两端的电压减少，根据C=可知，电容器极板电量减少，即放电；电容器右极板与电源负极相连，所以自由电子从a移动到b，故流过电流计G的电流方向为b→G→a．【解析】AB、含电容器的支路等效为断路，且两端的电压为并联部分的电压相等；当滑动触头P向右缓慢滑动的过程中，该电路的总电阻不变，但与电容器并联部分的电阻减少，即电容器两端的电压减少，根据C=可知，电容器极板电量减少，即放电，故A错误，B正确．CD、以上分析可知，电容器放电，且电容器右极板与电源负极相连，所以自由电子从a移动到b，电流的方向与电子的方向相反，故流过电流计G的电流方向为b→G→a，故C错误，D正确．。

含电容器电路的分析与计算方法
1、电路稳定后，由于电容器所在支路无电流通过，所以在此支路中的电阻上无电压降，因此电容器两极板间的电压就等于该支路两端的电压。

2、当电容器和电阻并联接入电路时，电容器两极板间的电压与其并联电阻两端的电压相等。

3、电路的电流、电压变化时，将会引起电容器的充（放）电。

如果电容器两端的电压升高，电容器将充电，反之则放电。

1、如图所示，电源两端电压为U＝10 V保持不变，R1＝4.0 Ω，R2
＝6.0 Ω，C1＝C2＝30 μF.先闭合开关S，待电路稳定后，再将S断
开，则S断开后，通过R1的电荷量为 ( )
A．4.2×10－4 C
B．1.2×10－4 C
C．4.8×10－4 C
D．3.0×10－4 C
2、如图16所示，两个相同的平行板电容器C1、C2用导线相连，开始都
不带电．现将开关S闭合给两个电容器充电，待充电平衡后，电容器C1
两板间有一带电微粒恰好处于平衡状态．再将开关S断开，把电容器C2两板稍错开一些(两板间距离保持不变)，重新平衡后，下列判断正确的是
A．电容器C1两板间电压减小
B．电容器C2两板间电压增大
C．带电微粒将加速上升
D．电容器C1所带电荷量增大
3、在如图所示，c1=6μF,c2=3μF,R1=3Ω,R2=6Ω，电源电动势E=18V，内阻不计，下列说法正确的是：
A.开关s断开时，a、b两点电势相等
B.开关s闭合后，a，b两点间的电流时2A
C.开关 s断开时C1带的电荷量比开关s闭合后C1带的
电荷量大
D.不论开关s断开还是闭合，C1带的电荷量总比C2带
的电荷量大。

含电容器电路问题解题方法
电是电路中常用的元件，也是初学者难以理解和掌握的部分。

对于电电路问题的解题，以下是一些方法和技巧：
1. 确认电的充电和放电过程
在解题过程中，首先需要确认电的充电和放电过程。

当电被连接到电源时，电会逐渐充电直至电压达到电源电压，过程中电流逐渐减少；当电从电源中断开时，电会逐渐放电。

2. 使用基本电路定律
在解题过程中，可以使用基本电路定律解决问题，例如欧姆定律、基尔霍夫定律等。

同时需要注意对带电体的电势移动方向的判断，通常是从正电荷移动到负电荷移动的方向计算电势差。

3. 考虑电的等效电路
对于复杂电路中的电，可以考虑将其转化为等效电路，以便于
理解和计算。

具体可以将电视为电容，使用电的计算公式计算等效
电容并代入电路。

4. 注意极性问题
在解决电电路问题时，需要注意电极性的问题，确保连接正确。

在电极性未标记的情况下，可以通过使用万用表测量电特性以及检
查电外形或包装上的标识来判断极性。

5. 多练多总结
最后，解决电电路问题需要多进行训练和练，总结解题思路和
方法，并不断提高自己的电路分析和计算能力。

以上是解决电容器电路问题的一些方法和技巧，希望对学习电
路和解决相关问题的人们有所帮助。

含容电路的计算专题分析含容电路问题是高考中的一个热点问题，在高考试题中多次出现。

同学们要要点提示复习。

1、求电路稳定后电容器所带的电量求解这类问题关键要知道：电路稳定后，电容器是断路的，同它串联的电阻均可视为短路，电容器两端的电压等于同它并联电路两端的电压。

【例1】在图16所示的电路中，已知电容C=2μF ，电源电动势E=12V,内电阻不计，R 1∶R 2∶R 3∶R 4=1∶2∶6∶3。

则电容器极板a 所带的电量为（ ）A 。

-8×10-6C B 。

4×10-6C C. —4×10-6C D 。

8×10—6C方法点拨：电路稳定后，电容C 作为断路看待，电路等价于R 1和R 2串联，R 3和R 4串联.由串联电路的特点得：211R R ER U AB +=， 即V R R E R U AB 4211=+=同理可得V R R ER U CD8433=+= 故电容C 两端的电压为：V U U U U U AB AD D B ab 4=-=-= 电容器极板a 所带的电量为：C CU Q ab a 6108-⨯==。

即D 选项正确。

2、求通过某定值电阻的总电量【例2】图17中，E=10V ，R 1=4Ω，R 2=6Ω，C=30μF，电池内阻可忽略。

(1)闭合电键K,求稳定后通过R 1的电流。

(2）然后将电键K 断开,求这以后流过R 1的总电量.方法点拨：（1）闭合电键K ，稳定后通过R 1的电流为:A R R EI 121=+=,电容器上电压为IR 2，储存的电量为 Q 1=CIR 2=1.8C 410-⨯(2） 电键K 断开后，待稳定后，电容器上电压为E,储存的电量为：Q 2=CE=3×10—4C 流过R 1的总电量为C Q Q Q 412102.1-⨯=-=∆【练1】在如图18所示的电路中，电源的电动势E=30V ，内阻r=1.0Ω,R 1=10Ω，R 2=10Ω,R 2=30Ω,R 3=35Ω，电容器的电容C=100μF，电容器原来不带电。