二次函数的系数符号问题

二次函数系数a、b、c与图像的关系知识要点二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0．（2）b由对称轴和a的符号确定：由对称轴公式x=判断符号．（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0．（4）b2-4ac的符号由抛物线与x轴交点的个数确定：2个交点，b2-4ac＞0；1个交点，b2-4ac=0；没有交点，b2-4ac＜0．（5）当x=1时，可确定a+b+c的符号，当x=-1时，可确定a-b+c的符号．（6）由对称轴公式x=，可确定2a+b的符号．一．选择题（共9小题）1．（2014?威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．42．（2014?仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③3．（2014?南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个4．（2014?襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．45．（2014?宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④6．（2014?莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2 B．m＜3 C．m＞3 D．2＜m＜37．（2014?玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个8．（2014?乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④9．（2014?齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个10、（2011?重庆）已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A、a＞0B、b＜0C、c＜0D、a+b+c＞011、（2011?雅安）已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结果①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，则正确的结论是（）A、①②③④B、②④⑤C、②③④D、①④⑤12、（2011?孝感）如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为（12，1），下列结论：①ac＜0；②a+b=0；③4ac-b2=4a；④a+b+c＜0．其中正确结论的个数是（）A、1B、2C、3D、4答案一．选择题（共9小题）1．（2014?威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：抛物线与y轴交于原点，c=0，（故①正确）；该抛物线的对称轴是：，直线x=﹣1，（故②正确）；当x=1时，y=a+b+c∵对称轴是直线x=﹣1，∴﹣b/2a=﹣1，b=2a，又∵c=0，∴y=3a，（故③错误）；x=m对应的函数值为y=am2+bm+c，x=﹣1对应的函数值为y=a﹣b+c，又∵x=﹣1时函数取得最小值，∴a﹣b+c＜am2+bm+c，即a﹣b＜am2+bm，∵b=2a，∴am2+bm+a＞0（m≠﹣1）．（故④正确）．故选：C．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．2．（2014?仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c ＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①当x=1时，y=a+b+c=0，故①错误；②当x=﹣1时，图象与x轴交点负半轴明显大于﹣1，∴y=a﹣b+c＜0，故②正确；③由抛物线的开口向下知a＜0，∵对称轴为0＜x=﹣＜1，∴2a+b＜0，故③正确；④对称轴为x=﹣＞0，a＜0∴a、b异号，即b＞0，由图知抛物线与y轴交于正半轴，∴c＞0∴abc＜0，故④错误；∴正确结论的序号为②③．故选：B．点评：二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0；（2）b由对称轴和a的符号确定：由对称轴公式x=﹣判断符号；（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0；（4）当x=1时，可以确定y=a+b+c的值；当x=﹣1时，可以确定y=a﹣b+c的值．3．（2014?南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．专数形结合．题：分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵图象开口向下，∴a＜0；故本选项正确；②∵该二次函数的图象与y轴交于正半轴，∴c＞0；故本选项正确；③∵二次函数y=ax2+bx+c的图象与x轴有两个不相同交点，∴根的判别式△=b2﹣4ac＞0；故本选项正确；④∵对称轴x=﹣＞0，∴＜0；故本选项正确；综上所述，正确的结论有4个．故选D．点评：本题主要考查了二次函数的图象和性质，解答本题关键是掌握二次函数y=ax2+bx+c系数符号的确定，做题时要注意数形结合思想的运用，同学们加强训练即可掌握，属于基础题．4．（2014?襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由函数y=x2+bx+c与x轴无交点，可得b2﹣4c＜0；当x=﹣1时，y=1﹣b+c＞0；当x=3时，y=9+3b+c=3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．解答：解：∵函数y=x2+bx+c与x轴无交点，∴b2﹣4ac＜0；故①正确；当x=﹣1时，y=1﹣b+c＞0，故②错误；∵当x=3时，y=9+3b+c=3，∴3b+c+6=0；③正确；∵当1＜x＜3时，二次函数值小于一次函数值，∴x2+bx+c＜x，∴x2+（b﹣1）x+c＜0．故④正确．故选C．点评：主要考查图象与二次函数系数之间的关系．此题难度适中，注意掌握数形结合思想的应用．5．（2014?宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④考点：二次函数图象与系数的关系．分析：根据抛物线开口方向得到a＞0，根据抛物线的对称轴得b=2a＞0，则2a﹣b=0，则可对②进行判断；根据抛物线与y轴的交点在x轴下方得到c＜0，则abc＜0，于是可对①进行判断；由于x=﹣2时，y＜0，则得到4a﹣2b+c ＜0，则可对③进行判断；通过点（﹣5，y1）和点（2，y2）离对称轴的远近对④进行判断．解答：解：∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x=﹣=﹣1，∴b=2a＞0，则2a﹣b=0，所以②正确；∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，所以①正确；∵x=2时，y＞0，∴4a+2b+c＞0，所以③错误；∵点（﹣5，y1）离对称轴要比点（2，y2）离对称轴要远，∴y1＞y2，所以④正确．故选D．点评：本题考查了二次函数图象与系数的关系：二次函数y=ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小，当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）．抛物线与y轴交于（0，c）．抛物线与x轴交点个数：△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．6．（2014?莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2 B．m＜3 C．m＞3 D．2＜m＜3考点：二次函数图象与系数的关系．分析：由于二次函数的对称轴在y轴右侧，根据对称轴的公式即可得到关于m的不等式，由图象交y轴于负半轴也可得到关于m的不等式，再求两个不等式的公共部分即可得解．解答：解：∵二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，∴m﹣3＜0，解得m＜3，∵对称轴在y轴的右侧，∴x=，解得m＞2，∴2＜m＜3．故选：D．点评：此题主要考查了二次函数的性质，解题的关键是利用对称轴的公式以及图象与y轴的交点解决问题．7．（2014?玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：∵抛物线的开口方向向下，∴a＜0；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即b2＞4ac，①正确；由图象可知：对称轴x==﹣1，∴2a=b，2a+b=4a，∵a≠0，∴2a+b≠0，②错误；∵图象过点A（﹣3，0），∴9a﹣3b+c=0，2a=b，所以9a﹣6a+c=0，c=﹣3a，③正确；∵抛物线与y轴的交点在y轴的正半轴上，∴c＞0由图象可知：当x=1时y=0，∴a+b+c=0，④正确．故选C．点评：考查了二次函数图象与系数的关系，解答本题关键是掌握二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．8．（2014?乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④考点：二次函数图象与系数的关系．分析：①由抛物线的对称轴为直线x=1，一个交点A（﹣1，0），得到另一个交点坐标，利用图象即可对于选项①作出判断；②根据抛物线开口方向判定a的符号，由对称轴方程求得b与a的关系是b=﹣2a，将其代入（3a+b），并判定其符号；③根据两根之积=﹣3，得到a=，然后根据c的取值范围利用不等式的性质来求a的取值范围；④把顶点坐标代入函数解析式得到n=a+b+c=c，利用c的取值范围可以求得n的取值范围．解答：解：①∵抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），对称轴直线是x=1，∴该抛物线与x轴的另一个交点的坐标是（3，0），∴根据图示知，当x＞3时，y＜0．故①正确；②根据图示知，抛物线开口方向向下，则a＜0．∵对称轴x==1，∴b=﹣2a，∴3a+b=3a﹣2a=a＜0，即3a+b＜0．故②错误；③∵抛物线与x轴的两个交点坐标分别是（﹣1，0），（3，0），∴﹣1×3=﹣3，=﹣3，则a=．∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），∴2≤c≤3，∴﹣1≤≤，即﹣1≤a≤．故③正确；④根据题意知，a=，=1，∴b=﹣2a=，∴n=a+b+c=c．∵2≤c≤3，≤≤4，≤n≤4．故④正确．综上所述，正确的说法有①③④．故选D．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点抛物线与x轴交点的个数确定．9．（2014?齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，∴对称轴在y轴的右侧，即：﹣＞0，∵a＞0∴b＜0，故①正确；②显然函数图象与y轴交于负半轴，∴c＜0正确；③∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），∴a﹣b+c=0，即a+c=b，∵b＜0，∴a+c＜0正确；④∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），且a＞0，∴当x=﹣2时，y=4a﹣2b+c＞0，故④正确，故选D．点评：主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．。

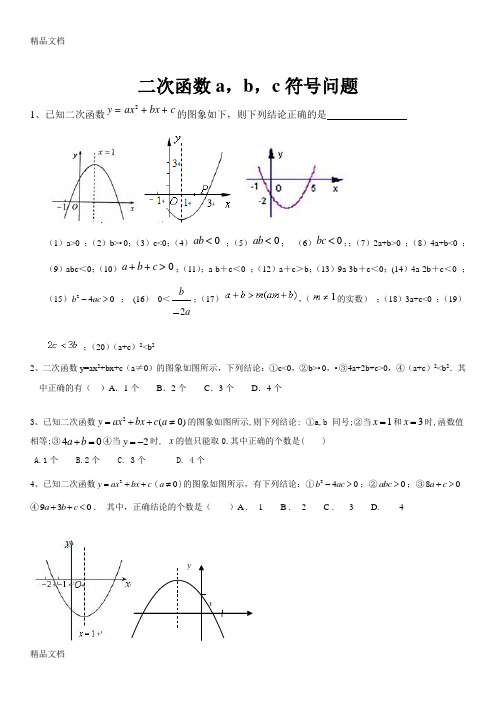
精品文档二次函数a ，b ，c 符号问题1、已知二次函数2y ax bx c =++的图象如下，则下列结论正确的是（1）a>0 ；（2）b>•0；（3）c<0；（4）0ab < ；（5）0ab <； （6）0bc <；；（7）2a+b>0 ；（8）4a+b<0 ；（9）abc ＜0；（10）0a b c ++>；（11）；a-b ＋c ＜0 ；（12）a ＋c ＞b ；（13）9a-3b ＋c ＜0；(14）4a-2b ＋c ＜0 ；（15）240b ac -> ； (16） 0＜a b 2；（17），（的实数） ；（18）3a+c<0 ；（19）；（20）（a+c ）2<b 22、二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，下列结论：①c<0，②b>•0，•③4a+2b+c>0，④（a+c ）2<b 2．其中正确的有（ ）A ．1个 B ．2个 C ．3个 D ．4个3、已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论: ①a,b 同号;②当1x =和3x =时,函数值相等;③40a b +=④当2y =-时, x 的值只能取0.其中正确的个数是( )A.1个B.2个C. 3个D. 4个4、已知二次函数2y ax bx c =++(0a ≠)的图象如图所示，有下列结论：①240b ac ->；②0abc >；③80a c +> ④930a b c ++<． 其中，正确结论的个数是（ ）A . 1 B . 2 C . 3 D . 411O y精品文档 5、已知二次函数2y ax bx c =++的图象如图所示，有以下结论：①0a b c ++<；②1a b c -+>；③0abc >；④420a b c -+<；⑤1c a ->其中所有正确结论的序号是（ ）A ．①②B ． ①③④C ．①②③⑤D ．①②③④⑤。

二次函数常见关系式符号的判定
二次函数是初中数学的重点内容之一，它的图像是由字母系数a、b、c的符号确定的，反之在给定抛物线的条件下如何确定字母系数的范围呢?现将二次函数的图像与字母系数的关系归纳如下：
（1）抛物线开口向上；抛物线开口向下．
（2）抛物线开口大小，越大开口越小
（3）、同号对称轴在轴左侧；、异号对称轴在轴右侧；=0对称轴为轴．
（4）抛物线与轴的交点在轴上方；抛物线与轴的交点在轴下方；
抛物线必过原点．
（5）抛物线与轴有两个交点；抛物线与轴有唯一交点；
抛物线与轴没有交点．
（6）的符号由点( 1，)的位置来确定；的符号由点( -1，)的位置来确定；
的符号由点(2，)的位置来确定。

例1如图1是抛物线的图像，则① 0；② 0；③ 0；④ 0；
⑤ 0；⑥ 0；⑦ 0。

解析：由图知：抛物线开口向下，；对称轴在轴左侧，、同号，故
；抛物线与轴的交点在轴上方，；点( 1，)、点( -1，)
分别在第四象限和第二象限，得<0, >0；抛物线与轴有两个交点，
得；由对称轴得=0．
例 2如图2，已知二次函数的图像与轴相交于(，0 )，(， 0)两点，
且，与轴相交于(O，-2)，下列结论：①；②；
③；④；⑤。

．其中正确结论的个数为( )
A．1个 B.2个 C.3个D．4个
解析：由图知：.当时，，所以，故③错误；因为抛物
线与轴有两个交点，所以即，所以④正确；当时，由图像得
，即，所以，故①错误；因为，又，所
以，故②错；当时，，即，所以故⑤错误．所以答案选 A．。

专题03 二次函数系数问题【知识点梳理】1、二次函数图象的特征与a ，b ，c 的关系2、常用公式及方法：（1）二次函数三种表达式：（2）韦达定理：若二次函数y =ax 2+bx +c 图象与x 轴有两个交点且交点坐标为（x 1，0）和（x 2，0），则x 1+x 2=−ba，x 1⋅x 2=ca。

（3）赋值法：在二次函数y =ax 2+bx +c 中，令x =1，则y =a +b +c ；令x =−1，则y =a −b +c ；令x =2，则y =4a +2b +c ；令x =−2，则y =4a −2b +c ；利用图象上对应点的位置来判断含有a 、b 、c 的关系式的正确性。

【典例分析】【例1】如图为二次函数y=ax2+bx+c的图象，在下列说法中：①ac＜0；②方程ax2+bx+c=0的根是x1=-1，x2=3；③a+b+c＜0；④当x＞1时，y随x的增大而减小；⑤2a-b=0；⑥b2-4ac ＞0．下列结论一定成立的是【答案】①②③⑥【解析】解：①由图象可知，a＞0，b＜0，c＜0，∴ac＜0，故①正确；②由图象可知，二次函数与x轴的交点横坐标为-1和3，∴方程ax2+bx+c=0的根是x1=-1，x2=3，故②正确；③当x=1时，y＜0∴a+b+c＜0，故③正确；④∵方程ax2+bx+c=0的根是x1=-1，x2=3∴对称轴为x=x1+x22=−1+32=1由图象可知，当x＞1时，y随x的增大而增大，故④错误；⑤∵对称轴−b2a=1∴b=-2a，2a+b=0，故⑤错误；⑥∵二次函数与x轴有两个交点，即方程ax2+bx+c=0有两个不相等的实数根，∴b2-4ac＞0，故⑥正确。

故答案为：①②③⑥【练1】如图，已知二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点，与y轴交于C 点，OA=OC．则由抛物线的特征写出如下结论：①abc＞0；②4ac-b2＞0；③a-b+c＞0；④ac+b+1=0．其中正确的个数是（）A.4个B. 3个C. 2个D. 1个【答案】B【解析】解：①由图象可知，a＞0，b＜0，c＜0，∴abc＞0，故①正确；②由图象可知，二次函数与x轴有两个交点，即方程ax2+bx+c=0有两个不相等的实数根，∴b2-4ac＞0，即4ac-b2＜0故②错误；③当x=-1时，y＞0∴a-b+c＞0，故③正确；④∵C（0，c），OA=OC，∴A（c，0）∴当x=c时，y=0，即（c）²+bc+c=0∵c≠0正确错误.故答案为：B.【练2】小明从二次函数y=ax2+bx+c的图象（如图）中观察得出了下面五条信息：①c＜0；②abc＞0；③a-b+c＞0；④2a-3b=0；⑤c-4b＞0．你认为其中正确的信息是（）A.①②③⑤B. ①②③④C. ①③④⑤D. ②③④⑤【答案】A【解析】解：①由图象可知，a＞0，b＜0，c＜0，故①正确；②abc＞0，故②正确；③由图象可知当x=-1时，y＞0∴a-b+c＞0，故③正确；④∵对称轴−b2a =13∴3b=-2a，2a+3b=0，故④错误；⑤∵当x=2时，y＞0即4a+2b+c＞0∵3b=-2a∴2×（-3b）+2b+c=c-4b＞0，故⑤正确.故答案为：A.【例2】抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=−1，其图象如图所示．下列结论：①abc<0；②(4a+c)2<(2b)2；③若(x1,y1)和(x2,y2)是抛物线上的两点，则当|x1+1|>|x2+1|时，y1<y2；④抛物线的顶点坐标为(−1,m)，则关于x的方程ax2+bx+c=m−1无实数根．其中正确结论的个数是（）A．4B．3C．2D．1【答案】B【解析】解：①∵抛物线图象开口向上，∴a>0，∵对称轴在直线y轴左侧，∴a，b同号，b>0，∵抛物线与y轴交点在x轴下方，∴c<0，∴abc<0，故①正确．②(4a+c)2−(2b)2=(4a+c+2b)(4a+c−2b)，当x=2时ax2+bx+c=4a+2b+c，由图象可得4a+2b+c>0，当x=−2时，ax2+bx+c=4a−2b+c，由图象可得，4a−2b+c<0∴(4a+c)2−(2b)2＜0，即，(4a+c)2<(2b)2故②正确．③|x1+1|=|x1−(−1)|，|x2+1|=|x2−(−1)|，∵|x1+1|>|x2+1|∴点(x1，y1)到对称轴的距离大于点(x2，y2)到对称轴的距离，∴y1>y2，故③错误．④∵抛物线的顶点坐标为(−1,m)，∴由图象知，y＞m，∴ax2+bx+c>m，∴ax2+bx+c=m−1无实数根．故④正确，综上所述，①②④正确，故答案为：B．【练1】二次函数y=ax2+bx+c(a≠0)的图象的一部分如图所示．已知图象经过点(−1,0)，其对称轴为直线x =1．下列结论：①abc <0；②4a +2b +c <0；③8a +c <0；④若抛物线经过点(−3,n )，则关于x 的一元二次方程()200ax bx c n a ++-=≠的两根分别为−3，5，上述结论中正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．4个【答案】C【解析】解：①由图象可知，a ＜0，b ＞0，c ＞0， ∴abc ＜0，故①正确；②∵对称轴为直线x = −b2a =1，且图象与x 轴交于点（﹣1，0）， ∴图象与x 轴的另一个交点坐标为（3，0），b=﹣2a ， ∴根据图象，当x =2时，y =4a +2b +c ＞0，故②错误；③根据图象，当x =﹣2时，y =4a ﹣2b +c =4a +4a +c =8a +c ＜0，故③正确； ④∵抛物线经过点(−3,n )，∴根据抛物线的对称性，抛物线也经过点(5,n )，∴抛物线y =ax 2+bx +c 与直线y =n 的交点坐标为（﹣3，n ）和（5，n ）， ∴一元二次方程ax 2+bx +c −n =0(a ≠0)的两根分别为−3，5， 故④正确，综上，上述结论中正确结论有①③④， 故答案为：C ．【练2】已知抛物线y =ax 2+bx +c （a,b,c 是常数，a ≠0）经过点(−1,−1),(0,1)，当x =−2时，与其对应的函数值y >1．有下列结论：①0abc >；②关于x 的方程ax 2+bx +c −3=0有两个不等的实数根；③a +b +c >7．其中，正确结论的个数是（ ） A ．0 B ．1C ．2D ．3【答案】D【解析】解：∵抛物线y =ax 2+bx +c （a,b,c 是常数，a ≠0）经过点(−1,−1),(0,1)，当x =−2时，与其对应的函数值y >1． ∴c =1＞0，a -b +c = -1,4a -2b +c ＞1， ∴a -b = -2,2a -b ＞0，∴2a-a-2＞0，∴a＞2＞0，∴b=a+2＞0，∴abc＞0，∵ax2+bx+c−3=0,∴△=b2−4a(c−3)=b2+8a＞0,∴ax2+bx+c−3=0有两个不等的实数根；∵b=a+2，a＞2，c=1，∴a+b+c=a+a+2+1=2a+3，∵a＞2，∴2a＞4，∴2a+3＞4+3＞7，故答案为：D．【例3】抛物线y=ax2+bx+c（a，b，c为常数）开口向下且过点A(1,0)，B(m,0)（−2< m<−1），下列结论：①2b+c>0；②2a+c<0；③ a(m+1)−b+c>0；④若方程a(x−m)(x−1)−1=0有两个不相等的实数根，则244ac b a-<．其中正确结论的个数是（）A．4B．3C．2D．1【答案】A【解析】解：∵抛物线开口向下，∴a<0把A(1,0)，B(m,0)代入y=ax2+bx+c得{a+b+c=0am2+bm+c=0，∴am2+bm=a+b∴am2+bm−a−b=0(m−1)(am+a+b)=0∵−2<m<−1∴am+a+b=0∴am=c,a(m+1)=−b∴c>0∴−1<m+1<0∵m+1<0∴−12<m+12<0∴−12<−b2a<0∴1>ba>0∴a<b<0①2b+c=2b−a−b=b−a>0，故①正确；②2a+c=2a−a−b=a−b<0，故②正确；③ a(m+1)−b+c=−2b+c=−2b−a−b=−3b−a>0，故③正确；；④若方程a(x−m)(x−1)−1=0有两个不相等的实数根，即ax2−a(m+1)x+am−1=0Δ=a2(m+1)2−4a(am−1)=a2(m+1)2−4a2m+4a=b2−4a2⋅−a−ba+4a=b2+4a2+4ab+4a=b2+4a(a+b)+4a=b2−4ac+4a>0∴4ac−b2<4a，故④正确，即正确结论的个数是4，故答案为：A．【练1】如图，抛物线y＝ax2＋bx＋c（a≠0）的顶点为（1，n），与x轴的一个交点B（3，0），与y轴的交点在（0，﹣3）和（0，﹣2）之间．下列结论中：①abc >0；②﹣2＜b<−53；③（a＋c）2﹣b2＝0；④2c﹣a＜2n，则正确的个数为（）A．1B．2C．3D．4【答案】B【解析】解：∵抛物线y＝ax2＋bx＋c（a≠0）的开口向上，∴a＞0，∵抛物线线y＝ax2＋bx＋c（a≠0）的顶点坐标为（1，n），∴对称轴x=−b2a=1，∴b=-2a＜0，∵抛物线与y轴的交点在（0，﹣3）和（0，﹣2）之间∴-3＜c＜-2＜0，>0；故①正确；∴abc∵抛物线线x轴的一个交点B（3，0），∴9a+3b+c=0，抛物线线x轴的一个交点（-1，0），∵b=-2a，∴c=3b2＜-2，∴-3＜3b2∴﹣2＜b<−4，故②错误；3∵抛物线线x轴的一个交点（-1，0），∴a-b+c=0，∴（a＋c）2﹣b2＝（a+b+c）（a-b+c）=0，故③正确；∵a＞0，∴-a＜0∵b=-2a∴3a+2b=-a＜0∴2c﹣a＞2（a+b+c），∵抛物线y＝ax2＋bx＋c（a≠0）的顶点为（1，n），∴a+b+c=n，∴2c﹣a＞2n；故④错误；故答案为：B【练2】已知二次函数y=ax2+bx+c的图像如图所示，有下列结论：①a＞0；②b2−4ac ＞0；③4a+b=0；④不等式ax2+（b−1）x+c＜0的解集为1≤x＜3，正确的结论个数是（）A．1B．2C．3D．4【答案】A【解析】解：∵抛物线的开口向上，∴a＞0，故①正确；∵抛物线与x轴没有交点∴b2−4ac＜0，故②错误∵由抛物线可知图象过（1,1），且过点（3,3）{a+b+c=19a+3b+c=3∴8a+2b=2∴4a+b=1，故③错误；由抛物线可知顶点坐标为（1,1），且过点（3,3）则抛物线与直线y=x交于这两点∴ax2+(b−1)x+c＜0可化为ax2+bx+c<x，根据图象，解得：1＜x＜3故④错误．故答案为：A．【练3】如图，已知抛物线y=ax2+bx+c的对称轴在y轴右侧，抛物线与x轴交于点A(−2,0)>0；②2b−4ac=1；和点B，与y轴的负半轴交于点C，且OB=2OC，则下列结论：①a−bc；④当−1<b<0时，在x轴下方的抛物线上一定存在关于对称轴对称的两点M，N（点③a=14M在点N左边），使得AN⊥BM．其中正确的有（）A．1个B．2个C．3个D．4个【答案】B【解析】解：①从图像观察，开口朝上，所以a>0，对称轴在y轴右侧，所以b＜0，图像与y轴交点在x轴下方，所以c<0<0，所以①不正确；∴a−b>0,a−bc②点A(−2,0)和点B，与y轴的负半轴交于点C(0,c)，且OB=2OC设B(−2c,0)代入y=ax2+bx+c,得：4ac2−2bc+c=0∵c≠0∴2b−4ac=1，所以②正确；③∵A(−2,0)，B(−2c,0)设抛物线解析式为：y=a(x+2)(x+2c)过C(0,c)∴c=4ac∴a=14，所以③正确；④如图：设AN,BM交点为P，对称轴与x轴交点为Q，顶点为D，根据抛物线的对称性，△APB是等腰直角三角形，∵A(−2,0)，B(−2c,0)∴AB=2−2c，PQ=12AB=1−c又对称轴x=−2+(−2c)2=c+1∴P(c+1,c−1)由顶点坐标公式可知D(c+1,4ac−b24a)∵a=14∴D(c+1,c−b2)由题意c−b2<c−1，解得b>1或者b<−1由①知b<0∴b<−1，所以④不正确．综上所述：②③正确共2个故答案为：B．【例4】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示，对称轴为x=12，且经过点(2,0)．下列说法：①abc<0；②−2b+c=0；③4a+2b+c<0；④若(−12,y1)，(52,y2)是抛物线上的两点，则y1<y2；⑤14b+c>m(am+b)+c（其中m≠12）．正确的结论有（）A．2个B．3个C．4个D．5个【答案】B【解析】解：∵抛物线的开口向下，与y轴的交点位于y轴正半轴，∴a<0,c>0，∵抛物线的对称轴为x =−b 2a =12，∴b=-a ＞0，∴abc <0，则结论①正确；将点(2,0)代入二次函数的解析式得：4a +2b +c =0，则结论③错误；将a =−b 代入得：−2b +c =0，则结论②正确；∵抛物线的对称轴为x =12，∴x =32和x =−12时的函数值相等，即都为y 1，又∵当x ≥12时，y 随x 的增大而减小，且32<52，∴y 1>y 2，则结论④错误；由函数图象可知，当x =12时，y 取得最大值，最大值为14a +12b +c =−14b +12b +c =14b +c ，∵m ≠12， ∴14b +c >am 2+bm +c ，即14b +c >m(am +b)+c ，结论⑤正确；综上，正确的结论有①②⑤，共3个，故答案为：B ．【练1】二次函数y =ax 2+bx +c (a ≠0)的图象如图所示，有下列结论：①0abc >，②4a −2b +c <0，③()a b x ax b -≥+，④3a +c <0，正确的有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C【解析】解：∵抛物线开口向下，∴a ＜0，∵对称轴为直线x =-1，即−b 2a =−1，∴b =2a ，则b ＜0，∵抛物线与y轴交于正半轴，∴c＞0，∴abc＞0，故①正确；∵抛物线对称轴为直线x=-1，与x轴的一个交点横坐标在0和1之间，则与x轴的另一个交点在-2和-3之间，∴当x=-2时，y=4a-2b+c＞0，故②错误；∵x=-1时，y=ax2+bx+c的最大值是a-b+c，∴a-b+c≥ax2+bx+c，∴a-b≥ax2+bx，即a-b≥x（ax+b），故③正确；∵当x=1时，y=a+b+c＜0，b=2a，∴a+2a+c=3a+c＜0，故④正确；故答案为：C．【练2】如图，二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0)，对称轴为x=−1，结合图象给出下列结论：①a+b+c=0；②a−2b+c<0；③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为-3和1；④若点(−4,y1)，(−2,y2)，(3,y3)均在二次函数图象上，则y1<y2<y3；⑤a−b<m(am+b)（m为任意实数）．其中正确的结论有（）A．1个B．2个C．3个D．4个【答案】C【解析】解：∵二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0)，∴当x=1时，a+b+c=0，故结论①正确；根据函数图像可知，当x =−1，y <0，即a −b +c <0，对称轴为x =−1，即−b 2a =−1，根据抛物线开口向上，得a ＞0，∴b =2a ＞0，∴a −b +c −b <0，即a −2b +c <0，故结论②正确；根据抛物线与x 轴的一个交点为(1,0)，对称轴为x =−1可知：抛物线与x 轴的另一个交点为(-3，0)，∴关于x 的一元二次方程ax 2+bx +c =0(a ≠0)的两根分别为-3和1， 故结论③正确；根据函数图像可知：y 2<y 1<y 3，故结论④错误；当x =m 时，y =am 2+bm +c =m(am +b)+c ，∴当m =−1时，a −b +c =m(am +b)+c ，即a −b =m(am +b)，故结论⑤错误，综上：①②③正确，故答案为：C ．【练3】如图，已知抛物线y =ax 2+bx +c （a ，b ，c 为常数，a ≠0）经过点(2,0)，且对称轴为直线x =12，有下列结论：①0abc >；②a +b >0；③4230a b c ++<；④无论a ，b ，c 取何值，抛物线一定经过,02c a ⎛⎫ ⎪⎝⎭；⑤2440am bm b +-≥．其中正确结论有（ ）A ．1个B ．2个C ．3个D ．4个【答案】D 【解析】解：①图像开口朝上，故a >0 ，根据对称轴“左同右异”可知0b <， 图像与y 轴交点位于x 轴下方，可知c <0∴abc >0故①正确；②x =−b 2a =12得a =−b∴a +b =0故②错误；③∵y =ax 2+bx +c 经过(2,0)∴4a+2b+c=0又由①得c <0∴4a +2b +3c <0故③正确；④根据抛物线的对称性，得到x =2与x =−1时的函数值相等∴当x =−1时y =0，即a −b +c =0∵a=-b∴2a +c =0即c 2a =−1∴y =ax 2+bx +c 经过(c 2a ，0)，即经过(−1,0)故④正确；⑤当x =12时,y =14a +12b +c , 当x =m 时,y =am 2+bm +c∵a >0∴函数有最小值14a +12b +c∴am 2+bm +c ≥14a +12b +c 化简得4am 2+4bm −b ≥0，故⑤正确．综上所述：①③④⑤正确．故选D ．【练4】已知二次函数y =ax 2+bx +c(a ≠0)的图象如图所示，有下列5个结论：①0abc ；②b 2<4ac ；③2c <3b ；④a +2b >m(am +b)（m ≠1）；⑤若方程|ax 2+bx +c |＝1有四个根，则这四个根的和为2，其中正确的结论有（ ）A ．2个B ．3个C ．4个D ．5个【答案】A【解析】解：①∵抛物线开口方向向下，∴a＜0，∵抛物线与y轴交于正半轴，∴c＞0，∵对称轴在y轴右侧，∴b＞0，∴abc＜0，①错误；②∵抛物线与x轴有两个交点∴b2−4ac>0∴b2>4ac，故②错误；③∵抛物线的对称轴为直线x=1，∴−b2a=1，∴a=−12b由图象得，当x=−1时，y=a−b+c<0，∴−12b−b+c<0∴2c<3b，故③正确；④当x=1时，y=a+b+c的值最大，∴当x=m(m≠1)时，a+b+c>am2+bm+c，∴a+b>m(am+b)（m≠1），∵b＞0，∴a+2b>m(am+b)（m≠1），故④正确；⑤∵方程|ax2+bx+c|=1有四个根，∴方程ax2+bx+c=1有2个根，方程ax2+bx+c=-1有2个根，∴所有根之和为2×（-ba ）=2×2aa=4，所以⑤错误．∴正确的结论是③④，故选：A【例5】函数y=x2+bx+c与y=x的图象如图所示，有以下结论：①b2﹣4c＞0；②b+c+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确的个数为A ．1B ．2C ．3D ．4【答案】B 【解析】解∵函数y=x 2+bx+c 与x 轴无交点，∴b 2﹣4c ＜0；故①错误．当x=1时，y=1+b+c=1，故②错误．∵当x=3时，y=9+3b+c=3，∴3b+c+6=0．故③正确．∵当1＜x ＜3时，二次函数值小于一次函数值，∴x 2+bx+c ＜x ，∴x 2+（b ﹣1）x+c ＜0．故④正确．综上所述，正确的结论有③④两个，故答案为：B【练1】已知抛物线y =ax 2+bx +c(a >0)，且a +b +c =−12,a −b +c =−32．判断下列结论：①abc <0；②220a b c ++>；③抛物线与x 轴正半轴必有一个交点；④当2≤x ≤3时，y 最小=3a ；⑤该抛物线与直线y =x −c 有两个交点，其中正确结论的个数（ ） A ．2B ．3C ．4D ．5【答案】D【解析】解：∵a +b +c =−12,a −b +c =−32，∴两式相减得b =12，两式相加得c =−1−a ，∴c <0，∵a >0,b >0,c <0，∴abc <0，故①正确；∴2a +2b +c =2a +2×12−1−a =a >0，故②正确；∵当x =1时，则y =a +b +c =−12，当x =-1时，则有y =a −b +c =−32， ∴当y =0时，则方程0=ax 2+bx +c 的两个根一个小于-1，一个根大于1， ∴抛物线与x 轴正半轴必有一个交点，故③正确；由题意可知抛物线的对称轴为直线x =−b 2a =−14a <0，∴当2≤x ≤3时，y 随x 的增大而增大，∴当x =2时，有最小值，即为y =4a +2b +c =4a +1−1−a =3a ，故④正确；联立抛物线y=ax2+bx+c及直线y=x−c可得：x−c=ax2+bx+c，整理得：ax2−1x+2c=0，2−8ac>0，∴Δ=14∴该抛物线与直线y=x−c有两个交点，故⑤正确；∴正确的个数有5个；故答案为：D．。