二次函数中的符号问题
- 格式:doc
- 大小:209.50 KB
- 文档页数:2







二次函数的符号问题教学目标:1.通过学习,掌握不同函数在同一坐标系中可能存在的大致图像2.通过主动探究的学习,提高学生的独立性,培养学生独立完成任务的意识3.通过分类讲解,提升学生自我认知能力,引导学生掌握二次函数a 、b 、c 与图像的关系重难点:能根据二次函数图像正确判断二次函数中系数的符号知识回忆:一、二次函数的概念一般地,如果y 与x 的关系满足:2(,,0)y ax bx c a b c a =++≠是常数,,那么y 叫做x 的二次函数。
二、二次函数的图象、开口方向及大小、对称轴、顶点坐标、增减性和最大最小值把二次函数2(,,0)y ax bx c a b c a =++≠是常数,解析式变化成()k h x a y +-=2的形式。
2224()24b ac b y ax bx c a x a a -=++=++ 新课知识:一、二次函数图像与系数a 、b 、c 关系技法:对于c bx ax y ++=2的图象特征与a 、b 、c 的关系为:①抛物线开口由a 定,上正下负;①对称轴位置a 、b 定,左同右异,b 为0时是y 轴;①与y 轴的交点由c 定,上正下负,c 为0时过原点。
1. 抛物线c bx ax y ++=2的图象如下图,则a 、b 、c 的符号为〔 〕A.0,0,0>>>c b a B.0,0,0=>>c b aC. 0,0,0=<>c b aD.0,0,0<<>c b a2. 假设a <0,b >0,c <0,则抛物线c bx ax y ++=2的大致图象为〔 〕3. 在同一直角坐标系内,二次函数()c x c a ax y +++=2与一次函数c ax y +=的大致图象,有且只有一个是正确的,正确的是〔 〕二、①的符号的判定ac b 42-的符号由抛物线与x 轴交点的个数确定:2个交点,042>-ac b ;1个交点,042=-ac b ;没有交点,042<-ac b4. 以下图中⊿0<的是〔 〕〔A 〕 〔B 〕 〔C 〕 〔D 〕5. 不管x 为何值,函数()02≠++=a c bx ax y 的值恒大于0的条件是( )A.a>0,①>0;B.a>0, ①<0;C.a<0, ①<0;D.a<0, ①<0 O y x O y x y x O yx O . .三、含a 、b 的代数式符号的判定 由对称轴公式a b x 2-=,可确定b a +2的符号 6.二次函数2(0)y ax bx c a =++≠的图象如下图,则①20a b +>①20a b +<①02b a-<①20a b -<①20a b ->中正确的___________.(请写出番号即可)7. 二次函数2(0)y ax bx c a =++≠的图象如下图,则以下说法不正确的是〔 〕A .240b ac ->B .0a >C .0c >D .02b a-< 四、含a 、b 、c 的代数式符号的判定当1=x 时,可确定c b a ++的符号,当1-=x 时,可确定c b a +-的符号当2=x 时,可确定c b a ++24的符号,当2-=x 时,可确定c b a +2-4的符号8. 如图,抛物线)0(2>++=a c bx ax y 的对称轴是直线1=x ,且经过点P 〔3,0〕,则c b a +-的值为〔 〕A. 0B. -1C. 1D. 29. 二次函数2y ax bx c =++〔0a ≠〕的图象如下图,有以下4个结论:①0abc >;①b a c <+;①420a b c ++>;①240b ac ->;其中正确的结论有〔 〕A .1个B .2个C .3个D .4个10. 抛物线c bx ax y ++=2的图象如下图,则以下结论正确的是〔 〕A .0>++c b aB .a b 2->C .0>+-c b aD .0<c –13 3 1 -1 O x =1 yx11. 抛物线c bx ax y ++=2中,b =4a ,它的图象如图,有以下结论:①0>c ; ①0>++c b a ①0>+-c b a①042<-ac b ①0<abc ①c a >4;其中正确的为〔 〕 A .①① B .①① C .①①① D .①①①知识小结: 二次函数y=ax 2+bx+c 系数符号确实定: 〔1〕a 由抛物线开口方向确定:开口方向向上,则a >0;开口向下,则a <0.〔2〕b 和a 共同决定对称轴的位置.(由对称轴公式x=判断符号.)a,b 同号时,对称轴在y轴左侧;a,b 异号时,对称轴在y 轴右侧;简称左同右异〔3〕c 由抛物线与y 轴的交点确定:交点在y 轴正半轴,则c >0;交点在y 轴负半轴,则c <0.交点在原点, c=0.〔4〕b 2-4ac 的符号由抛物线与x 轴交点的个数确定:2个交点,b 2-4ac >0;1个交点,b 2-4ac=0;没有交点,b 2-4ac <0.〔5〕当x=1时,可确定a+b+c 的符号,当x=-1时,可确定a-b+c 的符号.〔6〕由对称轴公式a b x 2-=,可确定b a +2的符号. 板书设计: 二次函数的符号问题复习 含a 、b 的代数式符号的判定a 、b 、c 与图像的关系 含a 、b 、c 的代数式符号的判定①的符号的判定 知识小结。
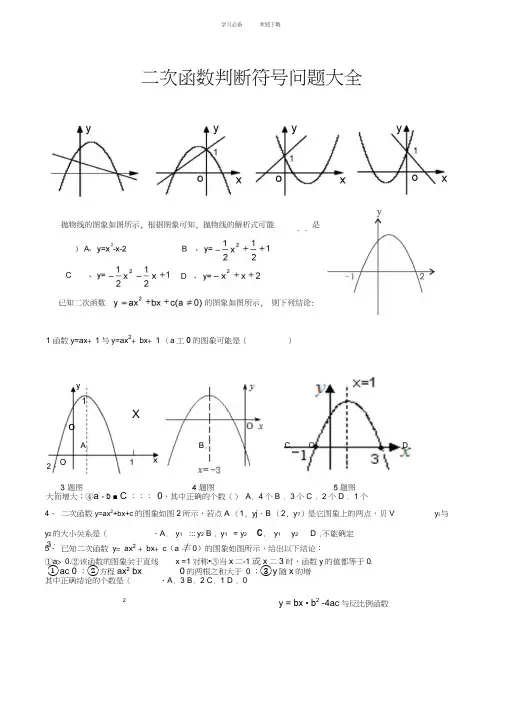
二次函数判断符号问题大全1 函数y=ax + 1与y=ax 2+ bx + 1 (a 工0的图象可能是()大而增大;④a - b ■ C ::: 0,其中正确的个数() A . 4个B . 3个C . 2个D . 1个4、 二次函数y=ax 2+bx+c 的图象如图2所示,若点A (1, yj 、B (2, y ?)是它图象上的两点,贝V y i 与y 2的大小关系是( 、A . y 1 ::: y 2 B . y 1 = y 2 C . y 1 y 2 D .不能确定 5、 已知二次函数 y = ax 2 + bx + c (a 丰0)的图象如图所示,给出以下结论: ①a > 0.②该函数的图象关于直线 x =1对称•③当x 二-1或x 二3时,函数y 的值都等于0. 其中正确结论的个数是( 、A . 3 B . 2 C . 1 D . 02y = bx • b 2 -4ac 与反比例函数1Xo2、(3、 A .B .C .D .①ac 0 ;②方程ax 2 bx 0的两根之和大于 0 ;③y 随x 的增6、二次函数y =ax bx c的图象如图所示,则一次函数在同一坐标系内的图象大致为(①b ::: 0②c0③b 2-4ac 0④a-b ,c :::0,其中正确的个数有()A . 1个B . 2个C . 3个D . 4个2①b :::0②c 0③b -4ac 0④a-b ,c :::O ,其中正确的个数有(2已知二(a = 0 )的图象如图4所示,有下列四个结论:7 题图 8 题图 9 题图8、已知=次函数y = ax 2 +bx+c 的图象如图.则下列5 个代数式:ac , a+b+c , 4a — 2b+c ,2a+b , 2a — b 中,其值大于0的个数为(B 3C 、4D 、52已知二次函数y = ax bx c(a = 0 )的图象如图所示,有下列四个结论:2a +b + c则一次函数 y = bx • b -4ac 与反比例函数 y 二10、二次函数y =ax bx c 的图象如图所示,A . 在同一坐标系内的图象大致为B .x C.xD .211、小强从如图所示的二次函数y =ax bx c 的图象中,观察得出了下面五条信息:(1) a ::: 0 ; (2)c 1 ; ( 3)b 0 ; ( 4) a b c 0 ;( 5)a-b ・c 0.你认为其中正确信息的个数有A . 2个B . 3个C . 4个D . 5个能是()14、 二次函数y =ax 2 bx c 的图象如图6所示,则下列关系式不正确的是A . a v 0B. abc >0C. a b c > 0D. b 2 -4ac > 02J严:1 11 i/O ! 4\212、二次函数 y =ax bx c (a = 0)的图象如图所示,对称轴是直线x = 1,则下列四个结论错误.的是13、在同一直角坐标系中,函数2B . 2a b=0C . b -4ac 0D . a -b c 02y = mx m 和函数 y = -mx 2x 2(m 是常数,且m = 0 )的图象可12题图15、已知二次函数y =ax - bx - c的图象如图所示,有以下结论:① a b : 0:② b c 1 :③abc 0 :④4a -2b • c ::: 0 :⑤c - a 1其中所有正确结论的序号是()A .①②B .①③④C .①②③⑤D .①②③④⑤15题图216、二次函数 y =ax bx c(a =0)B . b :: 017、二次函数y 二ax 2 - bx c 的图象如图所示,则下列关系式中错误的是()D . b 2 -4ac ::0 C . c : 0)。



二次函数的符号问题1.如图是二次函数y=ax 2+bx+c 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y 1),(1,y 2)是抛物线上两点,则y 1>y 2.其中说法正确的是( )2.如图,抛物线y =ax 2+bx +c (a ≠0)的顶点为D(-1,2),与x 轴的一个交点A 在点(-3,0)和(-2,0)之间,有四个结论:①b 2-4ac <0;②a +b +c <0;③2c -b =4;④方程ax 2+bx +c -2=0有两个不相等的实数根.其中正确结论有()A.1个B.2个C.3个D.4个3.二次函数2y ax bx c =++(a≠0)的图象如图,其对称轴为x =-1,有下面五个结论:①b >0;②24b ac ->0;③c=-3a ;④4a -2b+c >0;⑤对于图象上的两个不同的点(m ,n )、(-1,k ),有n k >.其中正确结论有()A .2个B .3个C .4个D .5个4.抛物线2y ax bx c =++图象如图所示,给出下列四个结论:①abc >0;②2a b c ++=;③12a >;④b <1.其中正确的结论是(????)(A )①②??(B )②③??(C )②④??(D )③④5.函数y=x 2+bx+c 与y=x 的图象如图所示,有以下结论:①b 2﹣4c >0;②b+c+1=0;③3b+c+6=0;④当1<x <3时,x 2+(b﹣1)x+c <0.其中正确的个数为( )6.小轩从如图所示的二次函数y=ax 2+bx+c (a ≠0)的图象中,观察得出了下面五条信息:①ab >0;②a+b+c <0;③b+2c >0;④a ﹣2b+4c >0;⑤.你认为其中正确信息的个数有( )7.已知二次函数y=ax 2+bx +c(a ≠0)的图象如图所示,有下列5个结论:①abc <0; ②b <a +c; ③4a +2b+c>0④2c <3b ;⑤a +b <m(am +b)(m≠1的实数)其中正确结论的序号有_____8.如图,二次函数y=ax 2+bx+c (a ≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab <0,②b 2>4a ,③0<a+b+c <2,④0<b <1,⑤当x >﹣1时,y >0,其中正确结论的个数是( )9.对于对称轴为x =-1的抛物线2(0)y ax bx c a =++≠,有下面五条信息:①2c =;②b =2a ;③24b ac ->0;④3a +b +c <0;⑤当x <-3时,y <0.其中正确信息的个数为()A.2个 B.3个 C.4个 D.5个2y ax bx c =++(0a ≠)的对称轴为直线2x =-,与x 轴和(4,0)-之间,其部分图象如图所示,则下列结论:①40a b -=;0>;④242a b at bt ->+(为实数);⑤点19(,)2y -,25(,)2y -,31(,)2y -是该抛物线上的点,则123y y y <<,正确的个数有().A.4个B .3个C .2个D .1个11.(2016中考)如图,抛物线y=ax 2+bx+c (a≠0)的对称轴为直线x=1,与x 轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac <b 2;②方程ax 2+bx+c=0的两个根是x 1=﹣1,x 2=3;③3a+c >0④当y >0时,x 的取值范围是﹣1≤x <3⑤当x <0时,y 随x 增大而增大,其中结论正确的个数是( )A .4个B .3个C .2个D .1个。
二次函数的图像与性质知识点:二次函数抛物线,图像对称是关键,开口、顶点和交点,它们确定图像现。
a 的正负开口判(开口大小由a 断),c 与y 轴来相见,b 的符号较特别,符号与a 相关联,顶点位置先找见,y 轴作为参考线,左同右异中为0,牢记心中莫混乱。
△的符号最简便,x 轴上数交点,顶点坐标最重要,一般配方它就现,横标即为对称轴,纵标函数最值现,若求对称轴位置,括中符号正相反,一般、顶点、交点式,不同表达能互换。
二次函数a ,b ,c 及相关问题的解决:1、 a 正负性:由开口方向决定,开口向上,a >0;开口向下,a <02、 b 的正负性:由于抛物线对称轴为ab x 2-=,所以b 的正负性与对称轴的位置和a 的正负性相关联。
对称轴在y 轴的左边时,a 、b 符号相同,对称轴在y 轴的右边时,a 、b 符号相反,对称轴为y 轴时,b=0(左同右异中为0)3、 c 的正负性:c 表示抛物线与y 轴交点的纵坐标,即当x=0时,y=c ,所以当抛物线与y 轴的交点在x 轴的上方时,c >0,当抛物线与y 轴的交点在x 轴的下方时,c <0。
(c 与y 轴来相见)4、 abc 的正负性:a ,b ,c 确定,则随之确定5、 ac b 42-=∆的正负性:△是根的判别式,由于一元二次方程是二次函数y=0的特殊情况,所以可以从抛物线与x 轴的交点个数来判断△的正负性,与x 轴有两个交点时,042>-ac b ,与x 轴的交点有一个时,042=-ac b ,与x 轴没有交点时,042<-ac b6、 利用x 的特殊值判断一些代数式的正负性:当x=1时,y=a+b+c ,当x=-1时,y=a-b+c ,当x=2时,y=4a+2b+c ,当x=-2时,y=4a-2b+c ,当x=3时,y=9a+3b+c ,当x=-3时,y=9a-3b+c ,对于取x 的特殊值得到代数式的正负性,重点看此时图像在x 轴的上方还是下方。
学号:_______ 姓名:____________【学习目标】1、能根据二次函数y =ax 2+bx +c 的图象确定a ,b ,c ,b 2-4ac ,a+b+c ,a-b+c 等代数式的符号.2、能解决二次函数中的简单的符号判断问题.【预习导航】1、已知二次函数2y ax bx c =++的图如图所示,则在“①0a <, ②0b >,③0c <,④240b ac ->”中正确的判断是( ) A .①②③④ B .④ C .①②③ D .①④2、已知二次函数2y ax bx c =++的图象如图所示,对称轴是1x =, 则下列结论中正确的是( ) A.0ac > B.0b <C.240b ac -<D.20a b +=3、根据右边二次函数y =ax 2+bx +c 的图象填空: (1)a _______0; (2)b _______0; (3)c _______0; (4) b 2-4ac _______0; (5) a+b+c _______0; (6) a-b+c _______0; (7) 4a +2b +c _______0; (8) 2a +b _______0.4、根据右边二次函数y=ax 2+bx+c 的图象填空: (1)a _______0; (2)b _______0; (3)c _______0; (4) b 2-4ac _______0; (5) a +b +c _______0; (6) a -b +c _______0; (7) 4a -2b +c _______0; (8) 2a -b _______0.预习小结:如何判断a ,b ,c ,b 2-4ac ,a+b+c ,a-b+c ,2a +b (或2a -b )的符号?x学号:_______ 姓名:___________【跟踪练习】1、在同一坐标系中一次函数y ax b =+和二次函数2y ax bx =+的图象可能为( )2、二次函数2y ax bx c =++的图象如图所示, 则直线y bx c =+的图象不经过( ) A.第一象限B.第二象限C.第三象限 D.第四象限3、二次函数y =(3-m )x 2-2mx -m 的图象如图所示,则m 的 取值范围是( ) A.m >0 B.m <0 C.m <3 D.0<m <34、二次函数()20y ax bx c a =++≠的图象如图所示.有下列结论:①240b ac -<;②0ab >;③0a b c -+=; ④40a b +=;⑤当2y =时,x 只能等于0.其中正确的是( ) A.①④ B.③④ C.②⑤D.③⑤5、小明从右边的二次函数2y ax bx c =++图象中,观察得出了 下面的五条信息:①0a <;②0c =;③函数的最小值为3-; ④当0x <时,0y >,⑤当1202x x <<<时,12y y >. 你认为其中正确的个数为( ) A.2 B.3 C.4 D.56、如图是二次函数y =ax 2+bx +c 图象的一部分,图象过点 A (-3,0),对称轴为x =-1.给出四个结论: ①b 2>4ac ;②2a -b =0;③a -b +c =0;④5a <b . 其中正确结论有_______________.【学习反思】判断二次函数中某些代数式的符号问题,你有哪些技巧、方法、规律?23-xOxyO x yOxyOxyAB C DO xyxyO0 2 5 x2y。
二次函数中的符号问题
一、基本知识:
(1)二次函数y=ax 2+bx+c 的图像是一条抛物线,这条抛物线的形状(开口方向、开口大小)是由 决定的. 抛物线的开口向上
抛物线的开口向下
抛物线的形状相同
(2)抛物线y=ax 2+bx+c 与y 轴的交点的位置是由 决定的.
抛物线与y 轴相交于正半轴上;
抛物线与y 轴相交于原点;
抛物线与y 轴相交于负半轴上.
(3)抛物线y=ax 2+bx+c 的对称轴的位置是由 决定的.
对称轴在y 轴的左侧;
对称轴在y 轴的右侧;
对称轴就是y 轴.
(4)抛物线与x 轴交点的个数由 决定的.
抛物线与x 轴有2个交点;
抛物线与x 轴有1个交点;
抛物线与x 轴有0个交点.
(5)二次函数y=ax 2+bx+c 的值恒大于0(或恒小于0)的条件是:
y 恒大于0
y 恒小于0
(6)抛物线y=ax 2+bx+c 的顶点坐标是( , )
顶点在x 轴上
顶点在y 轴上
二、例题:
例1、二次函数y=ax 2+bx+c(a ≠0)的图像如图所示,根据图像填空:
(用“>”、“=”、“<”填空 )
(1)a___0,b__0,c___0,(2)a+b+c_____0,a -b+c______0,
(3)
例2、二次函数y=ax 2+bx+c(a ≠0)的图像如图所示,根据图像填空:
(用“>”、“=”、“<”填空 )
(1)a___0;b___0;c___0;a+b+c___0;a -b+c______;
(2)
练习:
二次函数y=ax 2+bx+c(a ≠0)的图像如图所示,根据图像填空:
(用“>”、“=”、“<”填空 )
(1)a_____0,b____0,c_____0;
(2)a+b+c_____0,a -2b_____0,9a -3b+c_____0
c_____0b 21a 41+-1_____0b 2
1a 41--
例3、(1)已知二次函数y=ax2+bx+c中,如果a>0,b<0,c<0,那么这个
函数图像的顶点必在…()
A、第一象限
B、第二象限
C、第三象限
D、第四象限
(2)若二次函数y=ax2+bx+c的图像如图,已知图像与x轴的一个交点为(1,0),则下列各式中不成立的是…………()
A、b2-4ac>0
B、abc<0
C、a+b+c=0
D、a-b+c=0
(3)如图,x=1是y=ax2+bx+c的对称轴,则下列结论中正确的
是……()
A、a+b+c>0
B、b>a+c
C、abc<0
D、2a+b=0
(4)函数y=ax2+bx+c 的图像如图所示,则下列式子能成立的是()
A、abc>0
B、b<a+c
C、a+b+c<0
D、2c<3b
例4、(1)函数y=ax+m,y=a(x+m)2+k图像大致是…………()
(2)函数y=ax2和y=a(x-2)(a≠0)在同一坐标系里的图像大致是………………()
A、B、C、D、
(3)若一次函数y=ax+b的图像经过第二、三、四象限,则二次函数y=ax2+bx-3的大致图像是…()
A、B、C、D、
(4)y=ax+b与y=ax2+b在同一坐标系内的图像大致是………………………()。