多自由度系统近似计算方法
- 格式:doc
- 大小:499.00 KB
- 文档页数:6

第六章 多自由度系统固有频率和主振型的两种近似解法从多自由度问题的精确解的求解过程可知,求振系的固有频率及主振型是一项必不可少的过程,当自由度较少时,可直接求固有频率及主振型,但当自由度较多时,关于固有频率的求解就很复杂,如一个16自由度的振动问题,仅为展开频率方程的行列式,就需要进行720次计算,当然这些计算可借助计算机解决,但关于固有频率的近似计算及其计算思想,在实际应用及理论研究中仍具有一定的意义。
本章主要介绍求固有频率的两种方法:矩阵迭代法及传递矩阵法。
6-1矩阵迭代法矩阵迭代法适合于自由度较多的复杂系统,该法可以同时计算出系统的固有频率和相应的主振型,当自由度很多,但只要计算出低阶的几个频率时,矩阵迭代法很为适用,其大量的计算可由计算机完成。
在第五章已经介绍过,多自由度无阻尼系统的振动微分方程有两种形式,一种是用刚度矩阵建立的,其固有频率和主振型可由下式求,[]{}[]{}{}02=-A M p A K或写成[]{}[]{}A M p A K 2= (6-1)另一种是用柔度矩阵建立的,其固有频率和主振型可由下式求出{}[][]{}{}012=-A M R A p 或写成{}[][]{}A M R A p=21(6-2) 用[]1-M 前乘(6-1)式,得[]1-M []{}{}A p A K 2= (6-3)方程(6-2)(6-3)可写成如下统一的形式[]{}{}A A D λ= (6-4)(6-4)式称为特征值问题的标准形式,即矩阵迭代法的基本迭代公式。
式中[]D 称为动力矩阵,λ则是矩阵[]D 的特征值,当[]D 是按刚度矩阵形成时,即[][][]K M D 1-=,则λ表示固有频率的平方,λ=p 2,而当[]D 是按柔度矩阵形成时,即[][][]K R D =,则λ表示固有频率的平方的倒数,λ=1/p 2。
显然,任一阶固有频率和主振型都是(6-4)式的精确解。
下面介绍从(6-4)式出发进行迭代的基本过程:1) 某个经过基准化了的初始迭代向量{}1A (所谓基准化就是选取迭代向量的某个分量为基准值1),现选取{}1A ,使其第一个元素A 1,1为基准值1,并作[]{}1AD =运算,运算得到一个新的列阵{}1B ,再将{}1B 基准化,即将新的列阵{}1B 中的各元素均除以B 1,1,可得[]{}{}{}21,111A B B A D ==2) 与{}2A ,如果{}1A ≠{}2A ,则重复上述步骤,以[]D 乘{}2A ,得[]{}{}{}32,122A B B A D ==3) 比{}2A 与{}3A ,如果{}3A ≠{}2A ,则继续重复上述步骤,以[]D 乘{}3A ,…,直到第k 次迭代[]{}{}{}1,1+==k k k k A B B A D ,当式中{}k A ={}1+k A 时停止,这时,特征值1λ=B 1,k ,而相应的特征向量就等于{}k A 。




第4章 多自由度系统振动分析的数值计算方法用振型叠加法确定多自由度系统的振动响应时,必须先求得系统的固有频率和主振型。
当振动系统的自由度数较大时,这种由代数方程求解系统固有特性的计算工作量很大,必须利用计算机来完成。
在工程中,经常采用一些简单的近似方法计算系统的固有频率及主振型,或将自由度数较大的复杂结构振动问题简化为较少阶数的振动问题求解,以得到实际振动问题的近似分析结果。
本章将介绍工程上常用的几种近似解法,适当地选用、掌握这类实用方法,无论对设计研究或一般工程应用都将是十分有益的。
§4.1 瑞利能量法瑞利(Rayleigh )能量法又称瑞利法,是估算多自由系统振动基频的一种近似方法。
该方法的特点是:①需要假定一个比较合理的主振型;②基频的估算结果总是大于实际值。
由于要假设主振型,因此,该方法的精度取决于所假设振型的精度。
§4.1.1 第一瑞利商设一个n 自由度振动系统,其质量矩阵为[]M 、刚度矩阵为[]K 。
多自由度系统的动能和势能一般表达式为{}[]{}{}[]{}/2/2TTT x M x U x K x ⎫=⎪⎬=⎪⎭&& (4.1.1)当系统作某一阶主振动时,设其解为{}{}(){}{}()sin cos x A t x A t ωαωωα=+⎫⎪⎬=+⎪⎭&(4.1.2)将上式代入式(4.1.1),则系统在作主振动时其动能最大值max T 和势能最大值max U 分别为{}[]{}{}[]{}2max max /2/2TTT A M A U A K A ω⎫=⎪⎬=⎪⎭(4.1.3)根据机械能守恒定律,max max T U =,即可求得{}[]{}{}[]{}()2I TTA K A R A A M A ω== (4.1.4)其中,()I R A 称为第一瑞利商。
当假设的位移幅值列向量{}A 取为系统的各阶主振型{}i A 时,第一瑞利商就给出各阶固有频率i ω的平方值,即{}[]{}{}[]{}2(1,2,,)Ti i i Ti i A K A i n A M A ω==L(4.1.5)在应用上式时,我们并不知道系统的各阶主振型{}i A ,只能以假设的振型{}A 代入式(4.1.4),从而求出的相应固有频率i ω的估计值。




自由度计算方法
自由度是指一个系统中可以自由变化的参数的数量,它是衡量系统的复杂性的重要指标。
自由度的计算方法有多种,其中最常用的是拉格朗日乘子法。
拉格朗日乘子法是一种数学方法,它可以用来计算一个系统中可以自由变化的参数的数量。
该方法的基本思想是,将系统中的参数分解为一组乘子,每个乘子代表一个可以自由变化的参数,然后将这些乘子相乘,得到一个系统的总自由度。
拉格朗日乘子法的计算过程如下:首先,将系统中的参数分解为一组乘子,每个乘子代表一个可以自由变化的参数;其次,将这些乘子相乘,得到一个系统的总自由度;最后,将总自由度减去系统中的约束条件,得到最终的自由度。
拉格朗日乘子法的优点在于,它可以快速准确地计算出一个系统的自由度,而且它的计算过程简单易懂,易于实现。
此外,拉格朗日乘子法还可以用来计算复杂系统中的自由度,因为它可以将复杂系统中的参数分解为一组乘子,从而简化计算过程。
第5章多自由度系统的数值计算方法在工程实践中,我们经常会遇到多自由度系统(Multiple Degree of Freedom,简称MDOF)的问题,例如振动台、建筑结构等。
这些系统通常由多个自由度所组成,因此其运动方程会比单自由度系统更加复杂。
因此,我们需要使用数值计算方法来求解这些系统。
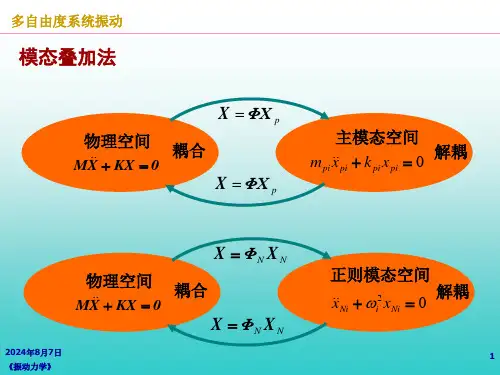
在本章中,我们将介绍两种常见的数值计算方法,包括直接积分法和模态叠加法。
一、直接积分法直接积分法,也称为时步法或时间积分法,是一种常用的求解MDOF系统的数值计算方法。
它的基本原理是将多自由度系统的运动方程转换为一组一阶常微分方程。
然后,利用数值积分方法,如欧拉法、Runge-Kutta法等,对这组常微分方程进行求解,得到系统的运动响应。
直接积分法的主要步骤如下:1.确定系统的运动方程:根据多自由度系统的动力学原理,可以得到系统的运动方程。
一般来说,这个方程是非线性方程,通常需要进行线性化处理。
2.将运动方程转化为一阶常微分方程组:将系统的运动方程进行适当的变换,将其转化为一组一阶常微分方程。
这样,就可以使用数值积分方法对其进行求解。
3. 选择数值积分方法:选择适合系统的数值积分方法,例如欧拉法、Runge-Kutta法等。
这些方法的基本思想是将微分方程转化为差分方程,通过迭代来逼近准确解。
4.进行数值计算:根据选择的数值积分方法,进行迭代计算,得到系统的运动响应。
尽管直接积分法是一种广泛应用的数值计算方法,但也存在一些问题。
例如,随着自由度的增加,计算量会大大增加。
此外,由于数值积分方法的局限性,可能会出现数值不稳定、数值发散等问题。
二、模态叠加法模态叠加法是求解MDOF系统的另一种常用数值计算方法。
该方法基于模态分析的思想,将MDOF系统的运动方程转化为一组无耦合的一自由度系统的运动方程。
然后,按照模态响应的叠加原理,将各个模态的响应相加,得到系统的总体响应。
模态叠加法的主要步骤如下:1.确定系统的模态参数:通过模态分析方法,可以得到系统的模态参数,包括模态频率、振型等。
目 录061001 振动理论 (3)061002 有限元原理及工程应用 (3)062019 非线性连续介质力学 (3)062020 高等断裂力学 (4)062021 非线性动力学现代理论 (4)062022 动力学系统建模 (5)062023 现代振动测试技术 (5)062024 固体力学非线性数值方法 (5)062025 电磁机械力学 (6)062027 高等计算力学 (6)062028 工程结构动力分析 (7)062029 现代控制理论基础 (7)062031 振动力学实验技术 (8)062032 振动信号数据处理 (8)062037 固体中的超声波 (9)062041 模态分析及综合应用技术 (9)062042 智能结构与振动控制 (10)062043 有限元方法与ANSYS应用 (10)062044 现代力学测量技术 (11)062046 复合材料力学分析 (11)062048 工程疲劳与断裂 (12)062053 材料的力学行为 (12)062054 飞行器总体设计 (12)062055 高等飞行动力学 (13)062057 复合材料结构设计 (13)062059 飞行器结构动力分析原理与实践 (14)062060 可靠性设计基础 (14)062061 气动弹性原理 (14)062063 计算流固耦合力学 (15)062097 飞行器气动设计原理与实践 (15)062098 结构多场数值分析与设计 (16)062099 飞行器控制系统设计与实践 (16)062100 力学测量与无损检测 (17)062101 声学理论与工程应用 (17)062102 纳米材料力学 (18)062103 损伤力学 (19)062104 爆炸与冲击动力学 (19)062105 高等弹性理论 (19)062106 飞行器制导与控制原理 (20)062107 燃烧理论 (20)062108 实验空气动力学 (21)062109 先进制造技术基础 (21)062110 计算空气动力学 (21)062111 导弹飞行动力学与动态特性分析 (22)062112 飞行器健康管理 (22)062113 高等动力学 (22)062114 航天航空遥感原理与应用 (23)062115 现代组合导航技术 (23)062116 计算流体力学与实践 (23)062117 多学科优化设计 (24)062118 非线性振动理论及工程应用 (25)062119 高速转子动力学 (25)062120 工程随机系统动力分析 (25)062121 轻质结构及热防护理论 (26)061001 振动理论本课程是研究模型系统动态特性的基础课程,使学生在机械振动理论和振动测试领域获得较为系统和全面的知识,主要内容为单自由度、多自由度和杆梁的线性振动(固有振动、自由振动和强迫振动)的基本理论,多自由度系统的近似计算方法,传感器技术,振动过程的实验测量基本方法,结构的模态试验与振动信号数据处理等。
固有频率的计算公式固有频率是指系统在没有外界干扰下,根据其自身的特性和参数计算得到的频率。
它可以用于描述机械、电子、光学等不同领域中的系统振动频率。
在物理学中,一般使用弹性力学理论来计算固有频率。
弹性力学是研究物体在受力作用下发生形变和振动的力学学科,其中固有频率的计算是其中一个重要的问题。
以下是计算固有频率的一些常见公式:1.自由振动的单自由度系统:对于一个自由振动的单自由度系统,固有频率可以通过以下公式计算:f=1/(2π)*√(k/m)其中,f表示固有频率,k表示系统的弹簧常数,m表示系统的质量。
2.自由振动的多自由度系统:对于一个自由振动的多自由度系统,固有频率可以通过以下公式计算:ω^2*x=K*x其中,ω表示固有角频率,x表示系统的位移矢量,K表示系统的刚度矩阵。
上述方程可以通过对系统动力学方程进行求解,得到系统的固有角频率和振型。
3.机械振动系统:对于机械振动系统,可以使用以下公式计算固有频率:f=1/(2π)*√(K/m)其中,f表示固有频率,K表示系统的刚度,m表示系统的质量。
在机械工程中,刚度可以通过计算杆件的刚度、弹簧的刚度、轮毂刚度等来确定。
4.电磁振动系统:电磁振动系统的固有频率可以通过以下公式计算:f=1/(2π)*√(1/LC)其中,f表示固有频率,L表示电感,C表示电容。
该公式适用于电路中的振荡电路,如LC振荡电路和LCR振荡电路。
除了上述公式,还有许多其他的计算固有频率的公式,具体的计算方法取决于系统的特性和参数。
需要根据具体情况选择合适的公式进行计算。
此外,在实际应用中,还可以通过实验的方法来测量固有频率,以获得更准确的结果。
在线性多自由度系统振动中,振动问题归结为刚度矩阵和质量矩阵的广义特征值问题,缺点:当系统自由度较大时,求解计算工作量非常大。
本章介绍邓克利法,瑞利法,里茨法,传递矩阵法等计算方法,可作为实用的工程计算方法对系统的振动特性作近似计算。
1、邓克利法由邓克利(Dunkerley )在实验确定多圆盘的横向振动固有频率时提出的,便于作为系统基频的计算公式 。
自由振动作用力方程:0KX XM =+ n R ∈X 左乘柔度矩阵F = K -1,位移方程:0X X FM =+ 定义D=FM 为系统的动力矩阵:0X XD =+ 作用力方程的特征值问题:φφM K 2ω= 位移方程的特征值问题:φφλ=D 特征值:22221n ωωω<<< ,n λλλ>>> 21 关系:2/1i i ωλ=位移方程的最大特征根:211/1ωλ=,对应着系统的第一阶固有频率。
位移方程的特征方程:0=-I D λ展开:0)()1(1111=++++---n n n nna a a λλλD tr d d d a nn -=+++-=)(22111例:022211211=--λλd d d d0)]()([)1(21122211221122=-++--d d d d d d λλ当 M 为对角阵时:)(FM D tr tr =∑==ni iii m f 1特征方程又可写为:0)())((21=---n λλλλλλ有:∑=-=ni i a 11λtrD -=∑=-=ni i ii m f 1∑∑===ni iii ni im f 11λ∑∑===ni i ii ni im f 1121ω如果只保留第 i 个质量,所得的单自由度系统的固有频率为:iii ii i m f m k 12==ω例:两自由度系统柔度矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+=2111111111k k k k kF (1)只保留 m 1 时1111k f =,1121m k =ω(2)只保留 m 2 时122122111k k k f =+=,21222m k =ω将2i ω代入:22221121111nni iωωωω+++=∑=对于梁结构系统,第二阶及第二阶以上的固有频率通常远大于基频,因此左端可只保留基频项,有:22221211111nωωωω+++≈例:三自由度系统⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0002223101220010*********x x x k x x x m 采用常规方法,固有频率:m k /3730.01=ω,m k /3213.12=ω,m k /0286.23=ω邓克利法当 m1 单独存在时:m k /21=ω 当 m2 单独存在时:k k k k k k 21212112=+=,m k /1222=ω当 m3 单独存在时:kk k k k 251111321123=++=,52123k k =,mk 523=ω代入邓克利法公式:22221211111nωωωω+++≈,mk /3535.01=ω2、瑞利法瑞利法是基于能量原理的一种近似方法,可用于计算系统的基频,算出的近似值为实际基频的上限,配合邓克利法算出的基频下限,可以估计实际基频的大致范围。
n 自由度保守系统:0KX XM =+ n R ∈X 主振动 :)sin(ϕω+=t φX 动能与势能:XM X TT 21=,KX X TV 21=最大值:φφM TT 2max 21ω=,φφK TV 21max =maxmax V T =得2)(ω==φφφφφM K TTR 成为瑞利商。
对于第 i 阶模态:2)()()()()()(i i Ti i Ti i R ω==φφφφφM K当φ为一般向量时(不是实际模态),总能展开为 n 个正则模态的线性组合:)()2(2)1(1n NN NNa a a φφφ+ ++==ϕφ∑==nj j Nja 1)(φaΦN =其中],,,[)()2()1(n N N N N φφφ =Φ,T n a a a ],,,[21 =a 代入瑞利商:aM ΦΦa a K ΦΦa N TN TN TN TR =)(ϕIaa Λa a TT =∑∑===nj jn j jjaa12122ω可以证明:21ω和 2n ω分别为瑞利商的极小值和极大值,即:221)(n R ωϕω≤≤ 分析:若将瑞利商右端分子内的所有j ω换为1ω,由于1ω是最低阶固有频率,因此:21121212)(ωωϕ=≥∑∑==nj j nj jaaR由瑞利商公式知,当)1(φ=ϕ确为第一阶模态时,有:21)(ωϕ=R 。
因此,瑞利商的极小值为21ω,同理可证明,瑞利商的极大值为2n ω 如果ϕ接近第 k 阶真实模态)(k φ=ϕ,比起 a k ,其它系数很小kj n j a a k j j ≠==,,,2,1 ,ε ,1<<j ε代入,得:∑=-+≈nj j k jkR 12222)()(εωωωϕ 例如 k =1,n j a a j j ,,21 ==,ε222212222222121)(nnn a a a a a a R ++++++=ωωωϕ21221222122122221222121a a a a a a n nn εεωεωεω++++++=约去a 1()222222222211nnn R εεωεωεωϕ++++++=分子上加减1项())1/()()(222212212321222122123212222222221n n n n n R εεωεωεωεωεωεωεωεωεωϕ+++⎪⎪⎭⎫⎝⎛+++-+++++++= 22222122222211)()1(nni i inεεωωεεεω+++-++++=∑= 22222122211)(nni i i εεωωεω+++-+=∑=∑=-+≈ni i i 2212221)(ωωεω因此,若ϕ与)(k φ的差异为一阶小量,则瑞利商与2k ω的差别为二阶小量。
对于基频的特殊情况,令k =1,则由于)~2(0212n j j=>-ωω瑞利商在基频处取极小值。
利用瑞利商估计系统的基频所得的结果必为实际基频的上限,ϕ愈接近系统的真实模态,算出的固有频率愈准确。
例题:接上例mk /3730.01=ω,采用邓克利法,基频:m k /3535.01=ω取在2m 质量上施加力P 所产生的“静变形曲线”作为近似的第一阶主振型,即:T]5.2,2,1[=ϕ代入瑞利商公式:mk R 142857.0)(=ϕ,mk 3780.01=ω与精确值相比,相对误差1.34%。
3、里茨法里兹法是瑞利法的改进,用里兹法不仅可以计算系统的基频,还可以算出系统的前几阶频率和模态,瑞利法算出的基频的精度取决于假设的振型对第一阶主振型的近似程度,而且得到的基频总是精确值的上限,里兹法将对近似振型给出更合理的假设,从而使算出的基频值进一步下降。
里兹法基于与瑞利法相同的原理,但将瑞利使用的单个假设模态改进为若干个独立的假设模态的线性组合:ΠA ηηηη==+⋯++=∑=rj j jr r aa a a 1)()()2(2)1(1ϕ,1)(⨯∈n i R ηrn r R⨯∈=],,,[)()2()1(ηηηΠ ,121],,,[⨯∈=r T r R a a a A代入瑞利商:)()(ΠA R R =ϕAM ΠΠA A K ΠΠA TTTT =AM A A K A T T=2ω=r r TR⨯∈=K ΠΠK ,r r T R ⨯∈=M ΠΠM由于()ϕR 在系统中的真实主振型处取驻值,所以 A 的各个元素应当从下式确定:)2,1(,0r j a R j⋯⋯==∂∂。
代入:),,2,1(,0)()(2r j a a TjTj⋯==∂∂-∂∂A M A A K A ω),,2,1(,2)(2)()()(r j a a a a TjTjjTTjTj ⋯==∂∂=∂∂+∂∂=∂∂A K e A K A A K A A K A A K A其中j e 是 r 阶单位矩阵的第 j 列。
上面 r 个方程可合成为:AK A K A A2)(=∂∂T表示将函数分别对 A 的各个元素依次求偏导,然后排列成列向量A∂∂。
同理,有:AM A M A A2)(=∂∂T两项代入得:0A M K =-)(2ω由于M K 、的阶数 r 一般远小于系统自由度数 n ,上式所示的矩阵特征值问题比原来系统的矩阵特征值问题解起来容易得多,因此里兹法实际上是一种缩减系统自由度求解固有振动的近似方法,M K 、就是自由度缩减为 r 的新系统的刚度矩阵和质量矩阵。
可求出 r 个特征根22221,,r ωωω⋯,,及相应的特征向量)()2()1(,,,r A A A ⋯,原来系统的前 r 阶固有频率可近似取为:),,2,1(,22r j j j ⋯==ωω,相应的前 r阶主振型近似取为:),,2,1(,)()(r j j j ⋯==ΠA ϕ。
正交性分析ji j Ti j T Ti j Ti ≠===当 0)()()()()()(AM AAM ΠΠAM ϕϕ即:00)()()()(==j T i j T i A K A A M A ,因此:得出的近似主振型式关于矩阵 M 和 K 相互正交。
例题:接前例采用常规方法,固有频率:mk /3730.01=ω,m k /3213.12=ω,m k /0286.23=ω采用邓克利法,基频:m k /3535.01=ω,采用瑞利法,基频:m k /3780.01=ω。
将假设的振型取为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡132211][21-==)()(ηηΠ 缩减后的新系统的刚度矩阵和质量矩阵:⎥⎦⎤⎢⎣⎡--=k kk k 20444TK ΠΠΚ=,⎥⎦⎤⎢⎣⎡--==m mm m TT 723M ΠΠM 特征值问题:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-+-+--0072044234αααα,km 2ωα=139853.01=α,860147.22=α,[]T1,927547.4)1(=A,[]T 1,018449.0)2(-=A固有频率:mk mk 373969.0111===αωω,mk mk 691197.1222===αωω主振型:[]T1860147.0430073.01)1()1(βϕ==ΠA[]T1860148.1930074.02)2()2(--==βϕΠA主振型精确值:[]T18608.04626.0)1(=φ,[]T17458.09339.2)2(--=φ里兹法得到的基频精度比用瑞利法的高,但第二阶固有频率的精度还欠佳。