毕萨定律及其应用
- 格式:ppt
- 大小:639.00 KB
- 文档页数:20

毕萨奥伐尔定律
摘要:
1.毕萨奥伐尔定律的简介
2.毕萨奥伐尔定律的公式及含义
3.毕萨奥伐尔定律在现实生活中的应用
4.毕萨奥伐尔定律的局限性及改进方法
5.总结
正文:
毕萨奥伐尔定律,又称“毕萨定律”,是由德国物理学家克劳斯·毕萨奥伐尔(Klaus Biauer)在1994年提出的一个定律。
该定律主要用于描述在固定压力下,流体通过管道时的流量与管道长度、管道直径之间的关系。
毕萨奥伐尔定律的公式为:Q = π/8 * d * √(2gh) ,其中Q表示流量,d 表示管道直径,g表示重力加速度,h表示管道长度。
在现实生活中,毕萨奥伐尔定律广泛应用于液体和气体的输送系统设计、优化及运行管理。
例如,在工业生产中,通过了解液体在管道中的流量,可以更好地控制生产过程;在农业生产中,利用毕萨奥伐尔定律可以优化灌溉系统,提高水资源利用率。
然而,毕萨奥伐尔定律也有其局限性。
首先,该定律适用于稳态流动,而在非稳态流动中,液体的流速与管道长度、直径的关系可能会发生改变。
其次,毕萨奥伐尔定律未考虑流体的黏性对流动的影响,因此在处理粘性流体时,需要对其进行修正。
为了解决这些问题,研究人员对毕萨奥伐尔定律进行了改进。
例如,引入了考虑流体黏性的修正系数,使得该定律在处理粘性流体时具有更好的准确性。
此外,还有一些研究者提出了基于毕萨奥伐尔定律的改进公式,以适应非稳态流动的计算需求。
总之,毕萨奥伐尔定律是一个具有广泛应用价值的定律,但在实际应用中也需要注意其局限性。


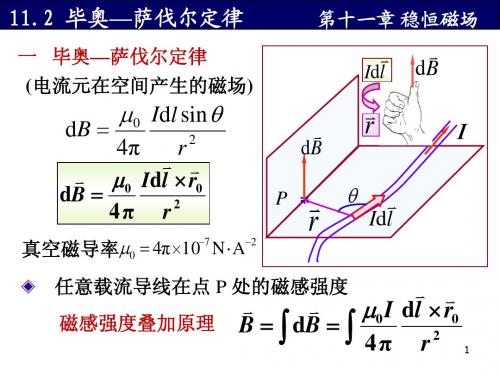
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例一、毕奥-萨伐尔定律1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。
微分形式为:整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。
磁感应线的方向服从右手定则,如图。
二、毕奥-萨伐尔定律应用举例两种基本电流周围的磁感应强度的分布:载流直导线;圆电流。
例1.载流长直导线的磁场解:建立如图坐标系,在载流直导线上,任取一电流元Idz,由毕-萨定律得元电流在P点产生的磁感应强度大小为:方向为垂直进入纸面。
所有电流元在P点产生的磁场方向相同,所以求总磁感强度的积分为标量积分,即:(1)由图得:,即:此外:,代入(1)可得:讨论:(1)无限长直通电导线的磁场:(2)半无限长直通电导线的磁场:(3)其他例子例2:圆形载流导线轴线上的磁场:设在真空中,有一半径为 R ,通电流为 I 的细导线圆环,求其轴线上距圆心 O 为 x 处的P点的磁感应强度。
解:建立坐标系如图,任取电流元,由毕-萨定律得:,方向如图:,所有dB形成锥面。
将dB进行正交分解:,则由由对称性分析得:,所以有:,因为: ,r=常量,所以:,又因为:所以:,方向:沿x轴正方向,与电流成右螺旋关系。
讨论:(1)圆心处的磁场:x=0 ,。
(2)当即P点远离圆环电流时,P点的磁感应强度为:。
例3:设有一密绕直螺线管。
半径为 R ,通电流 I。
总长度L,总匝数N(单位长度绕有n 匝线圈),试求管内部轴线上一点 P 处的磁感应强度。
解:建立坐标系,在距P 点 x 处任意截取一小段 dx ,其线圈匝数为: 电流为:。
其相当于一个圆电流,它在P点的磁感应强度为:。
因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右,所以整个螺线管在P点的磁感应强度的大小为:因为:代入上式得:所以:讨论:(1)管内轴线上中点的磁场:(2)当 L>>R时,为无限长螺线管。
此时,,管内磁场。
即无限长螺线管轴线上及内部为均匀磁场,方向与轴线平行满足右手定则。


毕奥——萨伐尔定律在极坐标系中的表达式及其应用
毕奥萨伐尔定律是世界上最经典的物理定律之一,它可以描述磁场在极坐标系中的表达式及其应用,是物理学中不可缺少的重要组成部分。
本文主要介绍毕奥萨伐尔定律在极坐标系中的表达式及其应用。
首先,我们来介绍毕奥萨伐尔定律在极坐标系中的表达式。
首先,毕奥萨伐尔定律定义了磁场从磁极出发的表达式,它表示磁场受到磁极强度的影响而产生,而且它的值取决于磁极的强度与磁极之间的距离,而这个距离关系可以用一个抛物线表达:即磁场强度随着距离的减小而增大,而随着距离的增加而减小,用公式表示为:B=B0*(1/r^2),其中B0为磁极强度,r为两磁极之间的距离。
此外,毕奥萨伐尔定律还可以描述磁场的产生方向,即它的向量表达式,它表明磁场是从磁极出发的,具体来说,磁场的方向是从磁极的正极指向负极的方向。
用公式表示为:B=B0*(1/r)*对应的单位
向量,其中B0为磁极强度,r为两磁极之间的距离,对应的单位向
量表示磁场方向。
接着,我们来讨论毕奥萨伐尔定律在极坐标系中的应用,首先,它可以用于研究磁性材料,因为磁性材料向外施加磁极的时候,磁场的变化遵循毕奥萨伐尔定律。
其次,毕奥萨伐尔定律可以用于研究空间磁场的变化,这对于放射性核物质的研究有着重要意义,因为空间磁场变化可以影响核子间的相互作用,从而影响放射性核物质的结构和品质,从而不同的空间磁场可以调节放射性核物质表现出不同的性质。
总而言之,毕奥萨伐尔定律可以描述磁场在极坐标系中的表达式及其应用,是物理学中不可缺少的重要组成部分。
它的表达式可以用简单的数学公式来描述,而它的应用范围也包括磁性材料和放射性核物质的研究。