毕萨定律
- 格式:pdf
- 大小:533.26 KB
- 文档页数:25


毕萨奥伐尔定律
摘要:
1.毕萨奥伐尔定律的简介
2.毕萨奥伐尔定律的公式及含义
3.毕萨奥伐尔定律在现实生活中的应用
4.毕萨奥伐尔定律的局限性及改进方法
5.总结
正文:
毕萨奥伐尔定律,又称“毕萨定律”,是由德国物理学家克劳斯·毕萨奥伐尔(Klaus Biauer)在1994年提出的一个定律。
该定律主要用于描述在固定压力下,流体通过管道时的流量与管道长度、管道直径之间的关系。
毕萨奥伐尔定律的公式为:Q = π/8 * d * √(2gh) ,其中Q表示流量,d 表示管道直径,g表示重力加速度,h表示管道长度。
在现实生活中,毕萨奥伐尔定律广泛应用于液体和气体的输送系统设计、优化及运行管理。
例如,在工业生产中,通过了解液体在管道中的流量,可以更好地控制生产过程;在农业生产中,利用毕萨奥伐尔定律可以优化灌溉系统,提高水资源利用率。
然而,毕萨奥伐尔定律也有其局限性。
首先,该定律适用于稳态流动,而在非稳态流动中,液体的流速与管道长度、直径的关系可能会发生改变。
其次,毕萨奥伐尔定律未考虑流体的黏性对流动的影响,因此在处理粘性流体时,需要对其进行修正。
为了解决这些问题,研究人员对毕萨奥伐尔定律进行了改进。
例如,引入了考虑流体黏性的修正系数,使得该定律在处理粘性流体时具有更好的准确性。
此外,还有一些研究者提出了基于毕萨奥伐尔定律的改进公式,以适应非稳态流动的计算需求。
总之,毕萨奥伐尔定律是一个具有广泛应用价值的定律,但在实际应用中也需要注意其局限性。

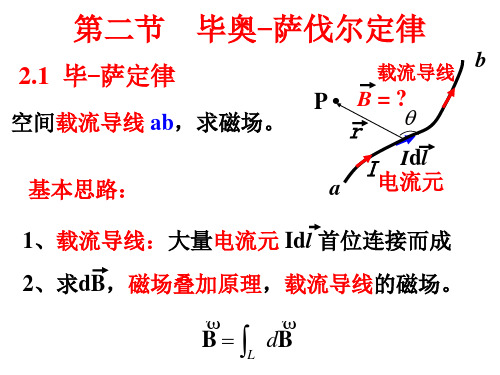
毕奥-萨伐尔定律公式
毕奥-萨伐尔定律公式是描述电磁感应现象的重要公式之一,它是由法国物理
学家毕奥和英国物理学家萨伐尔分别独立提出的,因此也被称为毕萨定律。
该定律表述了当一个闭合电路中的磁通量发生变化时,该电路内会产生电动势。
具体来说,如果一个电磁感应器中的磁通量Φ发生变化,那么在该感应器两端就
会产生一个电动势E,其大小与磁通量变化率的绝对值成正比。
毕奥-萨伐尔定律公式可以用一个简单的公式来表达:
E = -dΦ/dt
其中,E是感应电动势的大小,Φ是穿过感应电路的磁通量,t是时间,d/dt表示对时间的导数运算。
公式中的负号表示感应电动势的方向与磁通量变化的方向相反。
需要注意的是,该定律只适用于闭合电路中的感应电动势。
对于非闭合电路,根据法拉第电磁感应定律,产生的感应电动势大小与闭合电路中的相同,但方向可能不同。
总的来说,毕奥-萨伐尔定律公式是电磁学中一个非常重要的公式,广泛应用
于各种电磁感应现象的分析和设计中。

毕奥萨法定律
毕奥萨法定律是热力学的重要概念,它定义了一个系统的热力学状态受到外力作用后,可能发生的机制。
毕奥萨法定律最初由德国物理学家和化学家西蒙毕奥萨提出,被广泛应用于物理学、化学等学科,具有重要的科学价值和应用价值。
毕奥萨法定律由3个基本原理组成:
(1)第一定律:定容物体的热力学状态是恒定的,它的总能量恒定;
(2)第二定律:在一定温度和压力下,定容物体的总能不会改变,只会从一种形式(热能)转化为另一种形式(动能);
(3)第三定律:在恒定温度和压强下,一定体系中的熵总是不断增加,直到达到最大值。
毕奥萨法定律有以下3个特点:
(1)它是一个综合性定律,涵盖了动力学和热力学的微观规律,它成为统治物理学和化学的基础;
(2)它表明,一个体系受到外力作用后,不能仅仅受到能量的影响,还会受到熵的影响;
(3)它对绝热过程也有重要启示,即它表明,一个体系在绝热过程中,熵的增加是不可避免的,这也是热力学的终极定律。
毕奥萨法定律的重要性不言而喻。
它使我们能够更全面地理解热力学,从而帮助我们更准确地研究和预测物理现象。
它不仅可以应用于物理学,也可以应用于化学等学科,对于研究物理过程和本质有重
要作用。
此外,它还可以用于开发新型热力学技术,如热力学工艺技术、热交换技术等。
总之,毕奥萨法定律具有重要的科学价值和应用价值,是热力学的重要概念,也是物理学和化学的重要基础。
它的发现和发展,对人们研究物理和化学有重要意义,今后将具有更广泛的应用前景,并在更多领域发挥重要作用。