毕萨定律(解读
- 格式:ppt
- 大小:417.00 KB
- 文档页数:22

1820年,法国物理学家比奥特(Biot)和萨瓦特(Savart)通过实验,测量了一条长直电流线附近的小磁针的力定律,并发表了一篇论文,题为“传递给运动中的金属的电的磁化力”。
后来被称为比奥-萨瓦特定律。
后来,在数学家拉普拉斯(Laplace)的帮助下,该定律以数学公式表示。
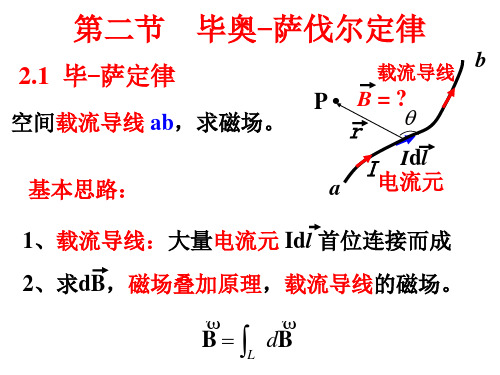
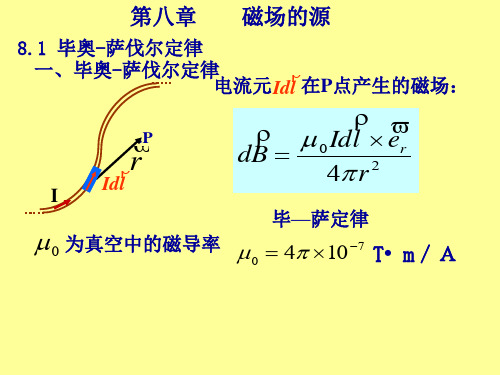
毕奥-萨伐尔定律:载流导线上的电流元Idl在真空中某点P的磁感度dB的大小与电流元Idl的大小成正比,与电流元Idl和从电流元到P点的位矢r之间的夹角θ的正弦成正比,与位矢r的大小的平方成反比。
dB的方向垂直于Idl和r所确定的平面,当右手弯曲,四指从方向沿小于π角转向r时,伸直的大拇指所指的方向为dB的方向,即dB、Idl、r三个矢量的方向符合右手螺旋法则。
叠加原理:
与点电荷的场强公式相似,毕奥——萨伐尔定律是求电流周围磁感强度的基本公式.磁感强度B也遵从叠加原理.因此,任一形状的载流导线在空间某一点P的磁感强度B,等于各电流元在该点所产生的磁感应强度dB的矢量和。
特点:
从课程论和物理学课自身特点的角度来分析毕奥-萨伐尔定律,它体现的学科特点有以下几点:(1)是稳恒电流磁场的关键知识点;(2)具有高度的抽象性;(3)使用数学工具的复杂性;(4)掌握“方法”比掌握“内容”更重要;(5)在探索知识的过程中体现“把握本质联
系,揭示事物发展内在规律性”的唯物辩证法观点。

毕萨奥伐尔定律
摘要:
1.毕萨奥伐尔定律的简介
2.毕萨奥伐尔定律的公式及含义
3.毕萨奥伐尔定律在现实生活中的应用
4.毕萨奥伐尔定律的局限性及改进方法
5.总结
正文:
毕萨奥伐尔定律,又称“毕萨定律”,是由德国物理学家克劳斯·毕萨奥伐尔(Klaus Biauer)在1994年提出的一个定律。
该定律主要用于描述在固定压力下,流体通过管道时的流量与管道长度、管道直径之间的关系。
毕萨奥伐尔定律的公式为:Q = π/8 * d * √(2gh) ,其中Q表示流量,d 表示管道直径,g表示重力加速度,h表示管道长度。
在现实生活中,毕萨奥伐尔定律广泛应用于液体和气体的输送系统设计、优化及运行管理。
例如,在工业生产中,通过了解液体在管道中的流量,可以更好地控制生产过程;在农业生产中,利用毕萨奥伐尔定律可以优化灌溉系统,提高水资源利用率。
然而,毕萨奥伐尔定律也有其局限性。
首先,该定律适用于稳态流动,而在非稳态流动中,液体的流速与管道长度、直径的关系可能会发生改变。
其次,毕萨奥伐尔定律未考虑流体的黏性对流动的影响,因此在处理粘性流体时,需要对其进行修正。
为了解决这些问题,研究人员对毕萨奥伐尔定律进行了改进。
例如,引入了考虑流体黏性的修正系数,使得该定律在处理粘性流体时具有更好的准确性。
此外,还有一些研究者提出了基于毕萨奥伐尔定律的改进公式,以适应非稳态流动的计算需求。
总之,毕萨奥伐尔定律是一个具有广泛应用价值的定律,但在实际应用中也需要注意其局限性。

“毕奥.萨伐尔”定律推导
毕奥·萨伐尔定律:
其中是从电流元指向参考点方向的单位矢量,是真空磁导率。
电流元产生的磁场的磁感应强度dB垂直Idl与e r组成的平面,并满足右手螺旋定则。
电流元
定义:Idl为电流元。
大小为Idl,的方向由线元所在处电流的流向来确定。
目的:用积分法来求出任意形状的磁场分布。
电流元的磁场
大小:
载流直导线的磁场
长为的载流直导线,其中电流为I,计算距离直导线为r0的P点的磁感应强度。
涉及到的数学公式
磁感应强度的积分推导
所以:
无限长载流直导线
则,
扩展知识:
磁现象
一切磁现象都源于电荷的运动。
一切磁力本质上都是电荷之间的作用力。
宇宙间四种基本作用力
1、引力又称重力,是四个基本相互作用中最弱的,但是同时又
是作用范围最大的。
而广义相对论中说引力是由于弯曲的空间和时间。
2、电磁力:世上大部分物质都具有电磁力,而磁与电是电磁力其中的一种表现模式。
3、强相互作用力又称为强核力,所有存在宇宙中的物质都是由原子构成,原子由电子和原子核组成,而原子核是由中子和质子组成。
4、弱相互作用力又称为弱核力,可以说是核能的另一种来源,主要是核子产生的天然辐射,四种相互作用力中,弱相互作用只比引力强一点。

简述毕奥萨伐尔定律
毕奥萨伐尔定律(Biossa-Fawer's law)是建筑物力学中的一项定律,它说明:支撑结构的垂直载荷或拉力大小与支撑结构的尺寸(或它的力学状态)之间存在着一定的关系。
换句话说,支撑结构的尺寸可以用来测量它所体现的垂直载荷或拉力的大小。
这个定律的定义是:一个结构件的最大垂向力(准确来说是最大结构备载)等于其端点的距离乘以另一个剪切力。
它可以用数学表达式来描述:F=Ld,其中F是结构的最大垂向力,L是其端点的距离,d是另一个剪切力。
毕奥萨伐尔定律还可以用来测量结构或系统的弯曲和扭转力,它可以用来确定结构或系统的最大受力情况,以便更好地设计其结构和系统。
这个定律也可以用来建立系统的力学分析,以便确定每个受力点的力和力矩。
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例一、毕奥-萨伐尔定律1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。
微分形式为:整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。
磁感应线的方向服从右手定则,如图。
二、毕奥-萨伐尔定律应用举例两种基本电流周围的磁感应强度的分布:载流直导线;圆电流。
例1.载流长直导线的磁场解:建立如图坐标系,在载流直导线上,任取一电流元Idz,由毕-萨定律得元电流在P点产生的磁感应强度大小为:方向为垂直进入纸面。
所有电流元在P点产生的磁场方向相同,所以求总磁感强度的积分为标量积分,即:(1)由图得:,即:此外:,代入(1)可得:讨论:(1)无限长直通电导线的磁场:(2)半无限长直通电导线的磁场:(3)其他例子例2:圆形载流导线轴线上的磁场:设在真空中,有一半径为 R ,通电流为 I 的细导线圆环,求其轴线上距圆心 O 为 x 处的P点的磁感应强度。
解:建立坐标系如图,任取电流元,由毕-萨定律得:,方向如图:,所有dB形成锥面。
将dB进行正交分解:,则由由对称性分析得:,所以有:,因为: ,r=常量,所以:,又因为:所以:,方向:沿x轴正方向,与电流成右螺旋关系。
讨论:(1)圆心处的磁场:x=0 ,。
(2)当即P点远离圆环电流时,P点的磁感应强度为:。
例3:设有一密绕直螺线管。
半径为 R ,通电流 I。
总长度L,总匝数N(单位长度绕有n 匝线圈),试求管内部轴线上一点 P 处的磁感应强度。
解:建立坐标系,在距P 点 x 处任意截取一小段 dx ,其线圈匝数为: 电流为:。
其相当于一个圆电流,它在P点的磁感应强度为:。
因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右,所以整个螺线管在P点的磁感应强度的大小为:因为:代入上式得:所以:讨论:(1)管内轴线上中点的磁场:(2)当 L>>R时,为无限长螺线管。
此时,,管内磁场。
即无限长螺线管轴线上及内部为均匀磁场,方向与轴线平行满足右手定则。
在静磁学中,毕奥-萨伐尔定律(英文:Biot-Savart Law)描述电流元在空间任意点P处所激发的磁场。
定律文字描述:电流元Idl 在空间某点P处产生的磁感应强度 dB 的大小与电流元Idl 的大小成正比,与电流元Idl 所在处到 P点的位置矢量和电流元Idl 之间的夹角的正弦成正比,而与电流元Idl 到P点的距离的平方成反比。
该定律在静磁近似中是有效的,并且与Ampère的电路规律和磁性高斯定律一致,以Jean-Baptiste Biot和FélixSavart命名。
定义在静磁学中,毕奥-萨伐尔定律(英文:Biot-Savart Law)描述电流元在空间任意点P处所激发的磁场。
定律文字描述:电流元Idl 在空间某点P处产生的磁感应强度dB 的大小与电流元Idl 的大小成正比,与电流元Idl 所在处到 P点的位置矢量和电流元Idl 之间的夹角的正弦成正比,而与电流元Idl 到P点的距离的平方成反比。
该定律在静磁近似中是有效的,并且与Ampère的电路规律和磁性高斯定律一致,以Jean-Baptiste Biot和FélixSavart命名。
电流(沿闭合曲线)毕奥-萨伐尔定律适用于计算一个稳定电流所产生的磁场。
这电流是连续流过一条导线的电荷,电流量不随时间而改变,电荷不会在任意位置累积或消失。
采用国际单位制,用方程表示:电流(整个导体体积)当电流可以近似为穿过无限窄的电线时,上面给出的配方工作良好。
如果导体具有一定厚度,则适用于Biot-Savart定律(再次以SI为单位):Biot-Savart:毕奥萨伐尔定律定律是实验定律,以一些简单的典型的载流导体产生的磁场为基础,经分析、归纳出的定律,而不是由电流元直接得出的,实际上不可能得到单独的电流元。