当前位置：文档之家 › 2.1毕萨定律求磁场

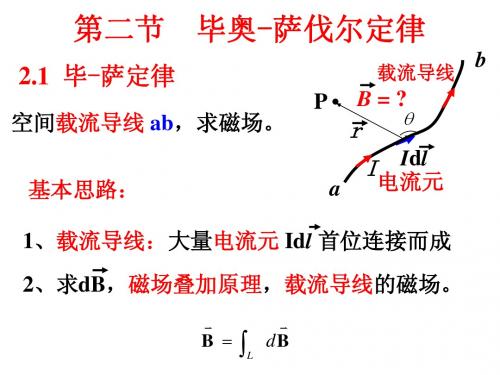
2.1毕萨定律求磁场

  • 格式：ppt
  • 大小：643.50 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

毕奥萨伐尔定律内容及公式(一)

毕奥萨伐尔定律内容及公式(一)

毕奥萨伐尔定律内容及公式(一)毕奥萨伐尔定律内容及公式毕奥萨伐尔定律简介毕奥萨伐尔定律（也称作毕奥-斯沃特定律）是电磁学中的一个重要定律，描述了电流所产生的磁场的特性。

由法国物理学家安德烈-玛丽-安普尔毕奥和德国物理学家卡尔-戴维德斯洛特共同发现并命名。

毕奥萨伐尔定律公式在真空中，毕奥萨伐尔定律可以用公式表达为：B = μ0 * I * (l / 2πr)其中， - B 是磁场的磁感应强度，单位为特斯拉（T）； - I 是载流导线的电流，单位为安培（A）； - l 是载流导线的长度，单位为米（m）； - r 是从载流导线测量到的点的距离，单位为米（m）；- μ0（读作mu-null）是磁导率，也称真空磁导率，约等于4π * 10^-7 T·m/A。

毕奥萨伐尔定律的解释与示例毕奥萨伐尔定律表明，电流所产生的磁场的强度与电流强度、导线长度以及距离的关系。

以下是一些示例来解释毕奥萨伐尔定律的应用：•示例一假设一段10米长的电缆中有电流流过，电流强度为5安培。

现在我们想要计算距离电缆1米处的磁场强度。

使用毕奥萨伐尔定律的公式，代入I=5A，l=10m，r=1m，以及μ0≈4π * 10^-7 T·m/A，我们可以计算得到：B = 4π *10^-7 * 5 * (10 / 2π * 1) = * 10^-6 T•示例二假设在一个闭合导线圈中有电流流过，导线圈的半径为米，电流强度为10安培。

现在我们想要计算导线圈中心的磁场强度。

使用毕奥萨伐尔定律的公式，代入I=10A，l=2π * （周长），r=，以及μ0≈4π * 10^-7 T·m/A，我们可以计算得到：B = 4π * 10^-7 * 10 * (2π * / 2π * ) = * 10^-6 T这些示例展示了应用毕奥萨伐尔定律计算不同条件下的磁场强度的过程。

通过理解该定律，我们可以更好地研究和应用电磁学中与磁场相关的现象和设备。

2 毕-萨定律05

2 毕-萨定律05
µ 0 IS B= = ⋅ 3 3 2π x 2x 载流圆弧， 圆心处的 处的B 载流圆弧，在圆心处的B =？ µ 0 IR 2
圆电流圆心 圆心O处 当 x = 0 ，圆电流圆心 处 BO =
µ0 I
I O R
S = πR
2
I
µ 0I l µ 0 I θ ( rad ) µ 0 I θ ( 0 ) B= = = 2 R 2π R 2 R 2π 2 R 360
b µ 0 I1 电流元处的磁场大小 B = 方向？ 方向？ 2πx v v v ( dF = I 2 d l2 × B1 ) 电流元受的安培力大小 电流元受的安培力 安培力大小 µ 0 I1 dF = B1 I 2 dl2 = I 2 dx 方向向上。 方向向上。 2πx
所有电流元受力都向上， 所有电流元受力都向上，合力 受力都向上
dx
µ0 dI
都向里
a
a + b − x
O
x
b
B=? I
y
R
x
无限长载流导半圆柱面 轴线上 B
θ
µ0 I = {− ln(a + b − x)} 2πa µ0 I a + b = ln 2πa b
dBx =
dx 2πa a + b − x
a 0
I dI = Rdθ πR
µ0 dI sin θ 2πR µ 0 dI cos θ 2πR
B = µ 0 nI
半无限长螺线管的端点， 左端 θ 1 = π / 2 θ 2 = 0 半无限长螺线管的端点， 右端 θ 1 = π θ 2 = π / 2 1 B = µ 0 nI
x = ctgθ R
R ( R 2 + x 2 )1/ 2

毕奥-萨伐尔定律 磁通量 磁场的高斯定理

毕奥-萨伐尔定律 磁通量 磁场的高斯定理
0 Idz sin B dB 4 r2
解：（1）判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D

2
z r 0 cot
dz
I

z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解： dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的，所以只能用它的矢量表示：
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体，其截面积为S，其 中载流子的密度为n，载流子带电 q，以漂移速度 v 运动。
毕奥—萨伐尔定律：
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o

r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )

2.1,2毕萨定律

2.1,2毕萨定律

磁 场
电
流
磁
铁
3、磁场的本源
磁 场
运动电荷
安培分子电流假说:组成物质的最小单元(磁分子)相当 于一个环形电流.当环形电流定向排列时,显示出磁性.
磁场是由运动电荷产生
四、安培定律 ( Amp` re e
ˆ 0 I1I 2 dl2 (dl1 r12 ) dF12 2 4 r12
作用力的大 小:
电流元: I1dl1、I 2 dl2
law)
1 dl1
n dl 2
r12
2
dF12
0 I1I 2 dl2 dl1 sin 1 sin 2 dF12 2 4 r12 作用力的方 向: ˆ dF12在dl1和r12组成的平面内，并与 dl2垂直 ˆ 0 I1I 2 dl1 (dl2 r21 ) ① dF21 dF12 , 2 4 r21
N
S
分子电流观点: 磁分子相当于一个环形电流, 当分子电流定向排列时,显示磁性.
§2.2 毕奥－萨伐尔定律
一、毕奥－萨伐尔定律
毕奥－萨伐尔根据电流磁作用的实验 结果分析得出，电流元产生磁场的规 律称为毕奥－萨伐尔定律。
Idl
r
1、内容 电流元Idl在空间P点产生的磁场B为：
0 Idl r ˆ dB 2 4 r
3、磁感应线(lines of magnetic induction)
六、解释磁现象的两种观点
磁荷观点: 认为磁极上存在正、负磁荷,有净 余磁荷,就产生磁场. 点磁荷之间的作用力大小为:
q m1 q m 2 F 4 0 r 2
磁场强度大小为:
F qm H qm 0 4 0 r 2 H Um H dl 0

毕奥萨伐尔定律求无限长直导线磁场

毕奥萨伐尔定律求无限长直导线磁场

毕奥萨伐尔定律求无限长直导线磁场嘿，伙计们，今天我们来聊聊一个非常有趣的话题：毕奥萨伐尔定律求无限长直导线磁场。

别看这个话题有点儿高深，其实咱们只要用点儿想象力和生活经验，就能轻松搞定它！咱们得知道毕奥萨伐尔定律是什么。

简单来说，这个定律就是告诉我们，一个无限长的直导线上，会产生一个磁场，而这个磁场的方向是这样的：从导线上的某一点出发，沿着直线方向，磁场线会越来越密，最后在导线的另一端达到一个峰值，然后又逐渐变得稀疏。

这个磁场的方向就像是一个指南针，总是指向北方。

为什么会出现这样一个磁场呢？这还得从电流说起。

咱们都知道，电流是由正电荷和负电荷组成的。

当正电荷和负电荷在导线中移动时，它们会产生一个磁场。

这个磁场的大小和方向取决于电流的大小、方向以及导线的形状。

而毕奥萨伐尔定律就是描述了这个磁场随着距离的变化而变化的规律。

现在，让咱们来看看这个磁场有什么用处吧。

咱们可以用它来制作电磁铁。

电磁铁是一种利用磁场产生力的特殊装置。

当我们给电磁铁通上电流时，它就会产生一个磁场，这个磁场会吸引或排斥其他物体。

这样一来，咱们就可以利用电磁铁来完成很多有趣的实验和工作了。

咱们还可以用这个磁场来制作电动机。

电动机是一种将电能转换为机械能的装置。

它的工作原理很简单：当电流通过导线时，导线会产生一个磁场，这个磁场会驱动电动机内的转子旋转，从而带动机械装置工作。

这样一来，咱们就可以利用电动机来驱动各种设备了。

咱们还可以用这个磁场来研究物理学的一些基本原理。

比如说，咱们可以通过观察毕奥萨伐尔定律来了解电流如何产生磁场，以及磁场如何影响电流的运动。

这样一来，咱们就可以更好地理解自然界的一些现象了。

毕奥萨伐尔定律虽然看起来有点儿复杂，但是只要咱们用点儿心去理解它，就会发现它其实是非常有趣的。

它不仅能帮助咱们解决实际问题，还能让我们更好地了解自然界的奥秘。

下次当你看到一根导线时，不妨想想它是如何产生磁场的，也许你会有意想不到的收获哦！。

2.2 磁感应强度 毕奥一萨伐尔定律

2.2 磁感应强度 毕奥一萨伐尔定律

实验结果：示零——不动，单位磁极受到的作用力矩相等。
结果分析： F1 H0 B1, F2 H0 B2 F1 B1 , F2 B2 单位磁极, H0=1，所以
1 2
F1r10 Br 1 10 1 F2 r20 B2 r20 B r 1 得到： 1 20 ， 即 ： B B2 r10 r0
两电流元——安培定律：
ˆ I I d l (d l r ) dF12 k 1 2 2 2 1 12 r 12 ˆ ˆ I d l (I d l r ) I dl r 0 2 2 21 1 12 I 2 d l2 0 1 1 12 ） （ 4 r 12 4 r 212 I 2 d l2 dB 0 I1d l1 r12 ˆ dB 4 r 212
电磁学电子教案
使用教材：
赵凯华、陈熙谋: 新概念物理学—电磁学
主讲：周贵德
沧州师范学院物电系
2012年2月修订
1
§2 磁感应强度 毕奥－萨伐尔定律
2.1 磁感应强度适量B
库仑定律： F 1 q1q2 ˆ r 2 4π 0 r
磁的库仑定律：
F
1 qm1qm 2 ˆ r 4πμ0 r 2
B

0
2
(cos 1 cos 2 )
B 0
B
0
2
16
几种载流导线的磁感应线
长直导线(电流元)
17
小结：

原则上，B-S定理加上叠加原理可以求任何载流导线在空 间某点的B 实际上，只在电流分布具有一定对称性，能够判断其磁场 方向，并可简化为标量积分时，才易于求解； 为完成积分，需要利用几何关系，统一积分变量； 一些重要的结果应牢记备用； 如果对称性有所削弱，求解将困难得多 如圆线圈非轴线上一点的磁场，就需要借助特殊函数 才能求解 又如在螺距不可忽略时，螺线管的电流既有环向分量 又有轴向分量，若除去密绕条件，就更为复杂。

2.毕奥--萨伐尔定律与静磁场


什 作 当 荷
§
2.2
电荷守恒定律
★ 系统总 电荷 保持不变； ◆ 电荷是物质的基本 属性 之一； ★ 电荷守恒定律是一条精确 、基 本的实验 定律； ★ 无论在化学反应还是原子核反应过程中，电荷守恒定律普 遍成立； ★ 电荷守恒定律的描述方法：
什 作 当 荷
§
2.2
电荷守恒定律
★ 系统总 电荷 保持不变； ◆ 电荷是物质的基本 属性 之一； ★ 电荷守恒定律是一条精确 、基 本的实验 定律； ★ 无论在化学反应还是原子核反应过程中，电荷守恒定律普 遍成立； ★ 电荷守恒定律的描述方法： ◆ 电流的连续性方程积分形式 J · dS = −
第二节
§
毕奥 {萨 伐尔 定律 与 静 磁 场
2.1
电流密度
磁 与 述
第二节
§
毕奥 {萨 伐尔 定律 与 静 磁 场
2.1
电流密度
磁 与 述
★ 电流密度的定义 J= dQ dI · eI = · eI dt dS cos θ dS cos θ I=
S
举 布 应
J · dS
电 间
第二节
§
毕奥 {萨 伐尔 定律 与 静 磁 场
S V
什 作 当 荷
∂ρ dV ∂t
任 进 项 荷 应
连 流
◆ 电流的连续性方程微分形式 J · dS =
S V
∇ · J dV = −
V
∂ρ dV ∂t
∂ρ +∇·J =0 ∂t
【讨论】
【讨论】 ★ 全空间总电荷守恒 d dt
从
ρ dV = 0
∞
【讨论】 ★ 全空间总电荷守恒 d dt
从
ρ dV = 0

毕奥萨伐尔定律求无限长直导线磁场

毕奥萨伐尔定律求无限长直导线磁场1. 引言：磁场的小秘密嘿，大家好！今天咱们来聊聊一个非常有趣的物理概念，毕奥萨伐尔定律。

这玩意儿听上去有点拗口，但其实没那么复杂，就像咱们生活中常见的事物一样，稍微一说，你就会明白。

你知道吗，磁场其实就像空气一样，虽然看不见，但无处不在，尤其是在电流通过的地方。

想象一下，如果你有一根无限长的直导线，电流从里面流过，嘿，那周围就会形成一个磁场，像是给这根导线披上了一层隐形的魔法斗篷！不过，咱们今天不聊魔法，而是来认真分析一下这道理，保证让你明白得透透的！2. 磁场的形成：像打水漂一样简单2.1 磁场是啥？首先，咱们得知道磁场到底是什么。

磁场就像是一种无形的力场，当电流流过导线的时候，周围的空间就会被一种看不见的“气场”充满。

这就好比你在水面扔个石头，水面上就会产生涟漪。

这里的电流就是石头，而磁场就是涟漪。

是不是很形象？所以，只要你有电流，磁场就会不请自来，跟影子一样，永远跟着你。

2.2 毕奥萨伐尔定律是什么？接下来，咱们来说说毕奥萨伐尔定律。

这个定律有点像一个小法则，它告诉我们怎么计算某一点的磁场强度。

简单来说，假设你在导线旁边的某个地方，毕奥萨伐尔定律就能告诉你那儿的磁场有多强。

具体公式是这样的：dB = (μ₀/4π) * (I * dl × r̂) / r²。

听起来复杂？别担心，我们一个个来解析。

这里面有个重要的概念，就是“μ₀”，也就是真空的磁导率，别问我是什么，反正就是个数字，能帮助我们计算！3. 磁场的计算：动手试试！3.1 无限长直导线的磁场好了，咱们来点实际的。

想象一下，你有一根无限长的导线，电流I从中流过。

根据毕奥萨伐尔定律，离导线r距离的点的磁场强度B，公式可以简化为B = (μ₀ * I) / (2π * r)。

简单明了吧？这里的r就像你跟导线的距离，离得越远，磁场就越弱，跟人走得远了，声音也听不清一样。

3.2 实际应用接下来咱们看看，这个磁场有什么用。

大学物理毕奥-萨伐尔定律


1
2
2
I
2 B
B 0I
4πr
3）延长线上的磁场
B=0
I
A
B
1
A
→r
r
＊p
B
+P
2、圆形载流导线（圆电流）轴线上的磁场（R, I）
Id l
o
IR
r dB d B
x
*
p dBx
x
dB'
解： （1）如图建立坐标系
（2）在导线上取电流元 Idl
dB
0
4π
Idl sin 900 r2
0 4
Idl r2
20
2
0, B 向外
0, B 向内
例7（例11-2） 一半径为R的无限长的半圆形金属薄片,沿轴 通有I 的电流,设电流在金属片上均匀分布,试求圆柱轴线上 任意一点P的磁感应强度.
解：将电流分割成许多无限长载流直导
线，电流为dI
I
利用无限长载流直导线的磁感应强度公式
B 0I
2πr
dB 0dI 2R
电流元中的运动电荷数
dN nSdl
电流元
Idl vSnqdl qv dN
将
Idl qv dN
代入上式得
从微观上看，电流元的dB就是dN个运动电荷共同产生的磁场
运动电荷的磁场
B
dB
0
qv r0
dN 4π r2
r0为电荷q到场点的矢径方向的单位矢量， 方向垂直于V，r确定的平面
是低速(v c)情形下匀速运动点电荷产生的磁场。
电流元 在空间P点产生的 磁感应强度 为
dB
k
Idl r2
r
0

电磁学毕奥-萨伐尔定律课件


1 π 2
cos 1 cos 2
cos 2
l/2
l / 22 R2
讨
B
论
0nI
cos2
0nI
2
l l 2 / 4 R2 1/2
l R
B 0nI
18
（2）无限长的螺线管（3）半无限长螺线管
1 π, 2 0
1 0.5π, 2 0
B 0nI
B 0nI / 2
1 2
0
nI
B 0nI
dB 0 dr
2
B 0
R
dr
0R
20
2
24
o 垂直于盘面的轴转动 ，求圆盘中心的磁
感强度.
22
向内 解法一 圆电流的磁场
0, B
向外
dI
2 π rdr
rdr
2π
dB 0dI 0 dr
2r 2
B 0 R dr 0R
20
2
0, B
23
END
v r
dB0
0
4π
dqv r2
dq 2解π法二rdr 运动电
荷的磁场
2 π x3
10
(1)
R
B0
x
推
Io
广 (2)
I
R
组
o×
合 (3) I
R ×o
B0
0I
2R
B0
0I
4R
B0
0I
8R
11
o
BA
0I
d
4πd
R1
R2
B0
0I I
4RA 2
0I
4R1
单击此处输入你的正文
I0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
CHAPTER II
恒磁场 THE MAGNETIC FIELD
1
在这一章里，我们要讨论磁场的源， 磁场的性质，磁场的效应 学习提示： 学习这一章，无论是方法还是结论 都和第一章有对称的地方 要注意区别磁场和电场

2
主要内容
磁场的概念 Ｂ的定义 毕萨定律 用毕萨定律求磁场 安培环路定理 用安培环路定理求磁场 磁场的高斯定理 磁场力 安培力 洛仑兹力 电流的磁场 运动带电粒子的磁场
18
Bz
o R 2 I
2( R r )
2 2 o 3 2
z
p
o I
2R
讨论
r0 0
B
ro
R I
p E
19
ro
2 ˆ 定义磁矩 P m IR S P e 电偶极矩 E P q l e 3 40 ro
2 o P m B 4ro3
ro

2
1
sin d
16
o I ro d sin o I B 2 2 2 L 4 sin ro / sin 4ro o I (cos 1 cos 2 ) 4ro
讨论

2
1
sin d
1 0 2
14
§２．毕萨定律
dB
Idl
r
Idl
0 I dl r dB 2 4 r dB dB p
有限长载流导线 闭合载流导线
ˆ o Idl r B dB 2 L L 4r o Idl r ˆ B dB 2 L L 4 r

3
§１
磁的基本现象和基本规律
电流的磁效应 奥斯特实验 Oersted Christian experiment
I
S N
4

一般磁现象The magnetic force
I
N S N
S
S
N
I I
B
I
I
5

磁场的概念The magnetic field
电场 电荷
电荷
磁场 运动电荷 运动电荷 磁场
Ｉ１ Ｉ２
dl2
dF12
r12
dF 12 sin 1
dl1
9
1
dl1
1
r12
n 2 dl2
dF12
dF 12 sin 2
I1dl1 I 2 dl2 sin 1 sin 2 dF 12 2 r12
10
I1dl1I 2 dl2 sin 1 sin 2 dF 12 k 2 r12 I 2 dl2 ( I1dl1 r12 ) 考虑到方向 dF12 k 2 r12

例３． 载流螺线管的磁场
dB R
2 2 2 3 2
o
R 2 In dl
2 [ R 2 ( x l )2 ]3 2 sin R
3
[R ( x l) ]
l
1

x l Rctg
R dl d 2 sin
p
R
2
o
x
dl
I
20
l
R2 [R ( x l) ]
B o nI
3.1 0, 2 / 2

x
–5R
5R
1 B 0 nI 2
B
螺线管的磁力 线
I
I
22

运动的带电粒子的磁场The field of a dB moving charge
o Idl r ˆ dB 2 4 r
Idl nqVSdl
7
若 dF 12 10 N
则 Ｉ＝１安培
12
用安培定律定义Ｂ
定义 则
I 2 dl2 ( I1dl1 r12 ) dF12 k 2 r12 0 I1dl1 r12 dB 2 4 r12
dF 12 I 2 dl2 dB
0 I dl r dB 2 4 r
dI 2rdl R sin d 2 r dI dB xR P R r 2[ r ( x y ) ] θ
2 e e
2
o
2
2
3
2
x
O
y
ω x
R sin d dB 2[ R x 2 Rx cos ]
4 2 0 e 2 2
3/ 2
24
令
u R x 3Rx cos
2 2
[4 x R (u R x ) ] dB . du u
2 2 2 2 2 3/ 2
B dB dB
0

R x 2
R x 2
2 B R 3
0 e
25
R
xR

P O x
r
θ y
ω
x
B dB dB
moving
q V
电流
电流
6
磁感应强度Ｂ
and B的比较 都描述场的基本性质 都可以有力线直观形象地描述 都有关于各自的通量和环流定理
E
7
安培定律及Ｂ的定义

电流元的概念 电流元之间的磁相互作 用规律
Ｉ１ Ｉ２
Idl
dl
B
I
8
I1dl1I 2 dl2 dF 12 2 r12
Idl
r
dN nsdl
ˆ o qV r ˆ dB o nqVSdl r 2 2 dN 4 nSdl r 4 r
这就是运动带电粒子的磁场
23

例:图为一均匀带电薄球壳,电荷密度为σe.现球壳以 角速度ω绕一直径转动,求球壳内外的磁场分布.
取细圆环如图,得等效电流
r
Idl
r
15
毕－萨定律的应用 例１．求载流直导线的磁场

o Idl sin B 2 L 4r
l r cos ro r sin
dl
I
l roo d / sin
o I ro d sin o I B 2 L 4 sin 2 ro / sin 2 4ro
两电流元间 讨论以下两电流元之间的作用力 的作用力不 满足牛顿第 三定律，但 是两环电流 之间的作用 力满足 11
电流强度单位的定义
令 k 0 4
I1dl1 I 2 dl2 sin 1 sin 2 dF 12 k 2 r12
取
7 2
I1 I 2 I r12 1m
0 4 10 N / A dl1 dl2 1m
B
I
17
o I B 2ro

例２．求载流圆环轴线上的磁场
o I 2 2 2 dB dl ; r ro R 2 4r
cos R R r
2 2 o
Bz dB cos
z
p
dB
ro
r
R I
o I cos Bz dl 2 4r
2 2 3 2
sin 3 R
2
1

p
R
2
o
3 2
x
dl
B
o
2
L2
L1
[R
R In dl
2
(x l) ]
2
I
B
o nI
2

2
1
sin d
B
o nI
2
(cos 1 cos 2 )
21
讨论
１．曲线
B
0.439
2.1 0, 2
一般地,电流元在磁场中受力为
dF I dl B
12 2 2
B大小等于单位长度,单位电流 元所受最大磁场力.方向为电流 元不受力所指的方向
13
量纲[MT2I1] 国际单位SI unit：1[T]=1tesla
1 tesla=1 newton/ampere.meter 1 tesla=104 gauss 中子星表面 108T 超导磁体附近 5Ｔ 地球表面 10-4 Ｔ
0
x R 2
x R 2
4 3
2 R 3 x
0 e
26