2017_2018学年高中数学课时跟踪训练(含答案)十三最大值最小值问题北师大版选修2_2

6 A . M >NB . M <N课时跟踪检测（十三） 不等关系与不等式层级一学业水平达标1 •李辉准备用自己节省的零花钱买一台学习机，他现在已存60元•计划从现在起以后每个月节省30元，直到他至少有 400元•设x 个月后他至少有 400元，则可以用于计算所需 要的月数x 的不等式是（ ）A . 30x — 60>400B • 30x + 60》400D . 30x + 40w 400解析：选B x 月后他至少有400元，可表示成30x + 60>400. 2 .若 abcd v 0,且 a >0, b > c , d v 0，则( )A . b v 0, c v 0B . b >0, c >0C. b > 0, c v 0D . 0v c v b 或 c v b v 0解析：选 D 由 a > 0, d v 0，且 abcd v 0,知 bc >0, 又■/ b >c ,「. 0v c v b 或 c v b v 0.3.已知：a , b , c , d € R,则下列命题中必成立的是 ()A. 若 a >b , c >b ,贝U a >cB. 若 a >— b ,贝V c — av c + ba bC. 若 a >b , c v d ,则一〉c d D. 若 a 2> b 2,则一a v — b解析：选B 选项A ,若a = 4, b = 2, c = 5,显然不成立，选项 C 不满足倒数不等式的条 件，女口 a >b >0, c v 0v d 时，不成立；选项 D 只有a >b >0时才可以.否则如 a =— 1, b = 0时不成立，故选B.0,由同向不等式相加得到一C. 30x — 60w 400 4 .设a € |0 , 亍，行0,nn,—牛的范围是A. 0,B.7t6，C.(0,7tD.7t6，7t解析：选D 0v 2 aVn , 0W -3wn35 .已知M 2x+ 1, N^ ,贝U M N的大小关系为（）寸1 + x6A. M>N B . M<NC. M= N D .不确定解析：选 A ••• 2x>0,「. M= 2x+ 1>1，而x2+ 1> 1,1 ,2三1，二M>N,故选A.1 + x6 .已知x v 1，则x2+ 2与3x的大小关系为 __________ .2解析：(x + 2) - 3x = (x—1)( x-2),因为x v 1,所以x- 1 v 0, x- 2v 0,所以(x- 1)( x- 2) >0,所以x2+ 2>3x.答案：x2+ 2>3x7 .比较大小：a2+ b2+ c2 ______ 2( a+ b+ c) - 4.2 2 2解析：a + b + c - [2( a+ b+ c) - 4]2 2 2=a + b + c - 2a- 2b- 2c+42 2 2=(a- 1) + (b- 1) + (c- 1) +1> 1> 0,Q Q Q故a + b + c > 2( a+ b+ c) - 4.答案：〉8 .已知一K x + y w4,且2< x- y w 3,贝U z= 2x- 3y的取值范围是_____________ (用区间表示).1 5解析：••• z= —2(x+ y) + 2( x-y),1 1 5 15-2w-2(x+ y) w2, 5w 2(x- y) ,1 5.3w- /x+ y) + 尹―y) w 8,••• z的取值范围是[3,8].答案：[3,8]9.若x工2或y工―1, M= x2+ y2- 4x + 2y, N=- 5，试比较M与N的大小.解：M- N= (x2+ y2- 4x + 2y) —( —5)2 2=(x -4x + 4) + (y + 2y+ 1)2 2=(x-2) + (y+ 1).因为(x-2)2> 0, (y+ 1)2> 0,所以(x-2)2+ (y+ J2》0,又因为x^2或y z—1,所以(x-2)2与(y + 1)2不会同时为0.所以(x-2)2+ (y+ 1)2> 0,所以M> Nb a10-⑴若a<b v 0，求证:a v b ；1 1(2)已知 a >b , -<匸，求证：ab >0.a b•/ a v b v 0,••• b + a v 0, b - a >0, ab >0,b + a b -a丄，b aObv 0,故 a v b .b — a 即 v 0,而 a > b ,「. b - a v 0,「. ab > 0.ab层级二应试能力达标1 •若 x € R , y € R,则()2222A . x + y >2xy — 1B . x + y = 2xy - 1 2 222C. x + y <2xy — 1D . x + y <2xy - 1解析：选 A 因为 x 2+ y 2- (2xy — 1) = x 2- 2xy + y 2 + 1 = (x — y )2+ 1>0,所以 x 2 + y 2>2xy — 1,故选 A.2. 已知 a 1€ (0,1) ,a 2 € (0,1)，记 M = a 1a 2, N= a 1 + a 2 1,则 M 与 N 的大小关系疋()A.M k NB . M >NC . M= ND . M> N解析：选 B a 1 € (0,1) , a 2€ (0,1) , • — 1<a 1 — 1<0, — 1<a 2—1<0,• M — N= a 1 a 2 — (a t+ a 2 — 1) = a 1a 2- a 1- a 2+ 1 = a(a 2— 1) — (a 2- 1) = (a — 1)( a 2 - 1)>0 ,• M^N,故选 B.3 •若一1<a <3 <1,则下列各式中恒成立的是 ( )A .— 2< a — 3 <0B . — 2< a — 3 < — 1 C.— 1< a — 3 <0D . — 1< a — 3 <1解析：选 A 由一1< a <1,— 1<3 <1,得一1<— 3 <1, • - — 2< a — 3 <2.又 T a < 3 ,故知—2< a — 3 <0. 4 .已知a , b , c 均为实数， ① a v b v 0,则 a 2v b 2； ② av c ,贝U a v bc ；证明:b a b 2- a 2⑴由于a -bb +ab -aababi i⑵―a vb ,i i a -bv 0,b③a>b,贝U c —2a v c—2b;1 1④ a> b ,则 a < b 上述说法正确的有（） A . 1个 B . 2个 C. 3个D . 4个解析：选A ①特殊值法.令 a =- 2, b =- 1，则4> 1，故①错; ② 当b v 0时，有a >be ,故②错；③ 当a > b 时，有—2a v- 2b ,从而e — 2a v e — 2b ,故③正确； 1 1④ 当a >0, b v 0时，显然有->-，故④错.a b综上，只有③正确，故选 A.15 .已知| a | v 1，则 许a 与1 - a 的大小关系为 _________ . 解析：由 | a | v 1,得一1 v a v 1. 1 + a > 0,1 — a > 0.1 — a 2.1 21 -0 v 1 — a w 1 ,•・1- a2> 1,16.已知不等式：① a v 0v b ;② b v a v 0；③ b v 0v a ;④ 0v b v a ;⑤ b v a 且 ab >0; ®a vb 且ab v 0.其中能使1 v -成立的是a b------------答案：①②④⑤⑥7.已知a , b € R, x = a 3— b , y = a 2b — a ,试比较x 与y 的大小.3222解：因为 x — y = a — b — a b + a = a (a — b ) + a — b = (a — b )( a + 1), 所以当a >b 时，x — y >0,所以x >y ; 当 a = b 时，x — y = 0,所以 x = y ;答案：1 1 + a 》1—a住》1—a . 解析:1 1 因为avbb —a ab v 0? b — a 与ab 异号 然后再逐个进行验证，可知①②④⑤⑥都当a<b 时，x—y<0,所以x<y.I?玉选做題8 .已知：f(x) = log a x, a> 1 > b> c> 0,证明：b-f c > c-f b b- c > a- c .证明：■/ a>b>c , • a- c>b-c>0 ,11…a-c <b-c，又;f (b) = log a b, f (c) = log a c, a> 1,••• f (b) >f(c),又•/ 1 > b>c> 0, • f (b) < 0, f (c) < 0 , • 0<- f (b) <- f (c),又b>c> 0 ,• b- f (c) >c —f (b) >0 ,1 1 b-f c c —f b又 > > 0 , •>——b-c a-c b- c a- c。

课时跟踪检测（九） 函数的最大值、最小值层级一 学业水平达标1．函数f (x )＝1x在[1,5)上( ) A ．有最大值，无最小值B ．有最小值，无最大值C ．有最大值，也有最小值D ．无最大值，也无最小值解析：选A 函数f (x )＝1x 在[1,5)上是减函数，∴函数f (x )＝1x 有最大值，无最小值．2．下列函数在[1,4]上最大值为3的是( )A ．y ＝1x ＋2B ．y ＝3x －2C ．y ＝x 2D ．y ＝1－x解析：选A 由函数性质知，B 、C 中的函数在[1,4]上均为增函数，A 、D 中的函数在[1,4]上均为减函数，代入端点值，即可求得最值，故选A.3．函数f (x )＝⎩⎪⎨⎪⎧2x ＋6，x ∈[1，2]，x ＋7，x ∈[－1，1)，则f (x )的最大值、最小值分别为( ) A ．10,6B ．10,8C ．8,6D ．以上都不对解析：选A 当1≤x ≤2时，8≤2x ＋6≤10，当－1≤x ＜1时，6≤x ＋7＜8.∴f (x )min ＝f (－1)＝6，f (x )max ＝f (2)＝10.4．若函数y ＝ax ＋1在[1,2]上的最大值与最小值的差为2，则实数a 的值是( )A ．2B ．－2C ．2或－2D ．0 解析：选C 当a ＞0时，y ＝ax ＋1在[1,2]上为增函数，∴(2a ＋1)－(a ＋1)＝a ＝2；当a ＜0时，y ＝ax ＋1在[1,2]上为减函数，∴(a ＋1)－(2a ＋1)＝－a ＝2，即a ＝－2.故a ＝2或－2.5．函数f (x )＝－x 2＋6x ＋8在[－2,1]上的最大值是( )A ．－8B ．13C ．17D ．8解析：选B f (x )＝－x 2＋6x ＋8＝－(x －3)2＋17，∴函数f (x )在[－2,1]上是增函数，∴f (x )的最大值为f (1)＝13.6．函数y ＝f (x )的定义域为[－4,6]，且在区间(－4，－2]上递减，在区间(－2,6]上递增，且f (－4)＜f (6)，则函数f (x )的最小值为________，最大值为________．解析：画出f (x )的一个大致图像，由图像可知最大值为f (6)，最小值为f (－2)．(或根据单调性和最大(小)值的定义求解)．答案：f (－2) f (6)7．函数y ＝1x －2，x ∈[3,4]的最大值为________． 解析：函数y ＝1x －2在[3,4]上是单调减函数，故y 的最大值为13－2＝1. 答案：18．函数f (x )＝x 2＋bx ＋1的最小值是0，则实数b ＝_____________________________. 解析：函数f (x )为二次函数，其图像开口向上，∴最小值为4－b 24×1＝0.∴b ＝±2. 答案：±29．已知函数f (x )＝|x |(x ＋1)，试画出函数f (x )的图像，并根据图像解决下列两个问题．(1)写出函数f (x )的单调区间；(2)求函数f (x )在区间⎣⎡⎦⎤－1，12的最大值．解：f (x )＝|x |(x ＋1)＝⎩⎪⎨⎪⎧－x 2－x ，x ≤0，x 2＋x ，x ＞0的图像如图所示． (1)f (x )的单调增区间是⎝⎛⎦⎤－∞，－12和[0，＋∞)，单调减区间是⎣⎡⎦⎤－12，0. (2)∵f ⎝⎛⎭⎫－12＝14，f ⎝⎛⎭⎫12＝34， ∴f (x )在区间⎣⎡⎦⎤－1，12的最大值为34. 10．已知函数f (x )＝2x x ＋1，x ∈[－3，－2]，求函数的最大值和最小值． 解：设－3≤x 1＜x 2≤－2，则f (x 1)－f (x 2)＝2x 1x 1＋1－2x 2x 2＋1 ＝2x 1(x 2＋1)－2x 2(x 1＋1)(x 1＋1)(x 2＋1)＝2(x 1－x 2)(x 1＋1)(x 2＋1). 由于－3≤x 1＜x 2≤－2，所以x 1－x 2＜0，x 1＋1＜0，x 2＋1＜0.所以f (x 1)－f (x 2)＜0，即f (x 1)＜f (x 2)．所以函数f (x )＝2x x ＋1，x ∈[－3，－2]是增函数． 又因为f (－2)＝4，f (－3)＝3，所以函数的最大值是4，最小值是3.层级二 应试能力达标1．已知函数y ＝k x在[2,4]上的最大值为1，则k 的值为( ) A ．2B ．－4C ．2或－4D ．4解析：选A 当k ＞0时，函数y ＝k x在[2,4]上为减函数， ∴k 2＝1，即k ＝2.当k ＜0时，函数y ＝k x 在[2,4]上为增函数，∴k 4＝1，即k ＝4.又∵k ＜0，∴k 无解．综上可知k ＝2.2．当0≤x ≤2时，a ＜－x 2＋2x 恒成立，则实数a 的取值范围是( )A ．(－∞，1]B ．(－∞，0]C ．(－∞，0)D ．(0，＋∞)解析：选C 令f (x )＝－x 2＋2x ＝－(x 2－2x ＋1)＋1＝－(x －1)2＋1(0≤x ≤2)，函数图像如图所示：∴f (x )最小值为f (0)＝f (2)＝0.而a ＜－x 2＋2x 恒成立，∴a ＜0.3．某公司在甲乙两地同时销售一种品牌车，利润(单位：万元)分别为L 1＝－x 2＋21x 和L 2＝2x (其中销售量单位：辆)．若该公司在两地共销售15辆，则能获得的最大利润为( )A ．90万元B ．60万元C ．120万元D ．120.25万元解析：选C 设公司在甲地销售x 台，则在乙地销售(15－x )台，公司获利为L ＝－x 2＋21x ＋2(15－x )＝－x 2＋19x ＋30＝－⎝⎛⎭⎫x －1922＋30＋1924， ∴当x ＝9或10时，L 最大为120万元．4．已知函数f (x )＝－x 2＋4x ＋a ，x ∈[0,1]，若f (x )的最小值为－2，则f (x )的最大值为( )A ．－1B ．0C ．1D ．2解析：选C 因为f (x )＝－(x －2)2＋4＋a ，由x ∈[0,1]可知当x ＝0时，f (x )取得最小值，即－4＋4＋a ＝－2，所以a ＝－2，所以f (x )＝－(x －2)2＋2，当x ＝1时，f (x )取得最大值为－1＋2＝1.故选C.5．函数y ＝|3x ＋1|在[－2,2]上的最大值为________．解析：y ＝|3x ＋1|＝⎩⎨⎧ －3x －1，－2≤x ≤－13，3x ＋1，－13＜x ≤2.当－2≤x ≤－13时，0≤－3x －1≤5； 当－13＜x ≤2时，0＜3x ＋1≤7. ∴0≤y ≤7，故其最大值为7.答案：7 6．函数f (x )＝x ＋1－1－x 的最大值为________．解析：函数的自变量x 需满足⎩⎪⎨⎪⎧x ＋1≥0，1－x ≥0， 解得－1≤x ≤1.因为y ＝x ＋1在区间[－1,1]上为增函数，y ＝1－x 在区间[－1,1]上为减函数，所以根据函数单调性的判断规律可得：f (x )＝x ＋1－1－x 在区间[－1,1]上为增函数，故f (x )max ＝f (1)＝ 2. 答案： 27．设函数f (x )＝⎩⎪⎨⎪⎧x 2－ax ＋5a ，x ≥2ax ＋5，x ＜2(a 为常数)． (1)对任意x 1，x 2∈R ，当x 1≠x 2时，f (x 1)－f (x 2)x 1－x 2＞0，求实数a 的取值范围； (2)在(1)的条件下，求g (x )＝x 2－4ax ＋3在区间[1,3]上的最小值h (a )．解：(1)由题意，函数在定义域上为增函数，则⎩⎪⎨⎪⎧ a 2≤2，a ＞0，22－2a ＋5a ≥2a ＋5，所以1≤a ≤4.故实数a 的取值范围为[1,4]．(2)g (x )＝x 2－4ax ＋3＝(x －2a )2＋3－4a 2，对称轴为x ＝2a ，由(1)得2≤2a ≤8.①当2≤2a ≤3，即1≤a ≤32时，h (a )＝g (2a )＝3－4a 2； ②当3＜2a ≤8，即32＜a ≤4时，h (a )＝g (3)＝12－12a . 综上，h (a )＝⎩⎨⎧3－4a 2，1≤a ≤32，12－12a ，32＜a ≤4.8．某市一家报刊摊点，从该市报社买进该市的晚报价格是每份0.40元，卖出价格是每份0.60元，卖不掉的报纸以每份0.05元的价格退回报社．在一个月(按30天计算)里，有18天每天可卖出400份，其余12天每天只能卖出180份．摊主每天从报社买进多少份，才能使每月获得最大的利润(设摊主每天从报社买进的份数是相同的)?解：设每天从报社买进x 份报纸，每月获利为y 元，则：y ＝0.20(18x ＋12×180)－0.35×12(x －180)＝－0.6x ＋1 188,180≤x ≤400，x ∈N.函数y ＝－0.6x ＋1 188在区间[180,400]上是减函数，所以当x ＝180时函数取最大值，最大值为y ＝－0.6×180＋1 188＝1 080.即摊主每天从报社买进180份时，每月获得的利润最大，最大利润为1 080元．。

2017-2018学年高中数学课时跟踪训练（十八）最大值、最小值问题北师大版选修1-1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017-2018学年高中数学课时跟踪训练（十八）最大值、最小值问题北师大版选修1-1）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017-2018学年高中数学课时跟踪训练（十八）最大值、最小值问题北师大版选修1-1的全部内容。

课时跟踪训练(十八）最大值、最小值问题1．函数f(x）＝错误!在x∈［2，4］上的最小值为（)A．0 B。

1 eC.错误!D.错误!2．函数f(x）＝x3－x2－x＋a在区间［0,2]上的最大值是3，则a的值为（）A．2 B．1C．－2 D．－13．已知函数f(x）＝ax－ln x，若f（x）>1在区间(1，＋∞）内恒成立，则实数a的取值范围是( )A．（－∞，1）B．（－∞,1]C．（1,＋∞) D．［1，＋∞）4.如图，将直径为d的圆木锯成长方体横梁，横截面为矩形，横梁的强度同它的断面高的平方与宽x的积成正比（强度系数为k，k＞0）．要将直径为d的圆木锯成强度最大的横梁，断面的宽x应为（）A。

错误! B.错误!C.错误!dD.错误!d5．已知函数f(x)＝x3－12x＋8在区间［－3，3］上的最大值与最小值分别为M，m,则M－m＝________.6。

如图,已知一罐圆柱形红牛饮料的容积为250 mL,则它的底面半径等于______时（用含有π的式子表示)，可使所用的材料最省．7．函数f（x）＝x3＋f′错误!x2－x.（1）求f（x)的单调区间;（2)求f（cos x）的最小值和最大值．8．某地建一座桥,两端的桥墩已建好，这两墩相距m米．余下工程只需建两端桥墩之间的桥面和桥墩．经测算,一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2＋错误!)x万元．假设桥墩等距离分布，所有桥墩都视为点，且不考虑其他因素．记余下工程的费用为y万元．(1）试写出y关于x的函数关系式；（2)当m＝640米时，需新建多少个桥墩才能使y最小?答案1．选C ∵f(x)＝错误!，∴f′(x）＝错误!＝错误!。

课时跟踪检测(二) 数列的函数特性层级一学业水平达标1．下列四个数列中，既是无穷数列又是递增数列的是（）A．1，错误!，错误!,错误!，… B．sin错误!，sin错误!，sin错误!，…C．－1，－错误!，－错误!，－错误!，… D．1，错误!,错误!，…,错误!解析：选C A是递减数列，B是摆动数列，D是有穷数列，故选C.2．已知数列{a n｝的通项公式是a n＝错误!，那么这个数列是( ) A．递增数列B．递减数列C．常数列D．摆动数列解析：选A a n＝错误!＝1－错误!，随着n的增大而增大．3．数列｛a n}中,a n＝－n2＋11n，则此数列最大项的值是( ）A。

错误!B．30C．31 D．32解析：选B a n＝－n2＋11n＝－错误!2＋错误!，∵n∈N＋，∴当n＝5或6时，a n取最大值30,故选B.4．数列｛a n}中，a1＝1,以后各项由公式a1·a2·a3·…·a n＝n2给出，则a3＋a5等于（）A。

错误!B。

错误!C。

错误! D.错误!解析：选C ∵a1·a2·a3·…·a n＝n2，∴a1·a2·a3＝9,a1·a2＝4，∴a3＝错误!。

同理a5＝错误!,∴a3＋a5＝错误!＋错误!＝错误!.5．已知数列｛a n}满足a1〉0，且a n＋1＝错误!a n，则数列{a n}的最大项是( )A．a1B．a9C．a10D．不存在解析：选A ∵a1>0且a n＋1＝错误!a n，∴a n〉0，错误!＝错误!〈1,∴a n＋1〈a n，∴此数列为递减数列，故最大项为a1.6．若数列｛a n}的通项公式为a n＝错误!(k>0，且k为常数），则该数列是________（填“递增”“递减”）数列．解析：错误!＝错误!·错误!＝错误!<1.∵k>0，∴a n〉0，∴a n＋1<a n，∴｛a n}是递减数列．答案：递减7．数列{－2n2＋9n＋3｝中最大项的值为________．解析：由已知a n＝－2n2＋9n＋3＝－2错误!2＋错误!。

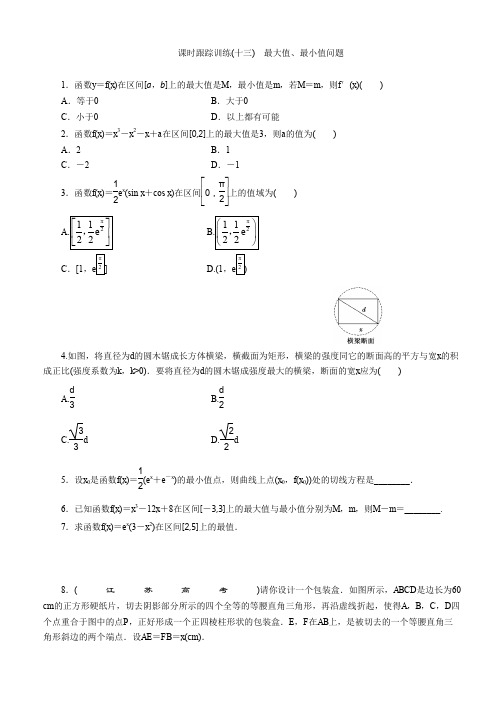
课时跟踪训练(十三) 最大值、最小值问题1．函数y ＝f (x )在区间[a ，b ]上的最大值是M ，最小值是m ，若M ＝m ，则f ′(x )( )A ．等于0B ．大于0C ．小于0D ．以上都有可能2．函数f (x )＝x 3－x 2－x ＋a 在区间[0,2]上的最大值是3，则a 的值为( )A ．2B ．1C ．－2D ．－13．函数f (x )＝12e x (sin x ＋cos x )在区间⎣⎢⎡⎦⎥⎤0，π2上的值域为( )C ．[1， D.(1，4.如图，将直径为d 的圆木锯成长方体横梁，横截面为矩形，横梁的强度同它的断面高的平方与宽x 的积成正比(强度系数为k ，k >0)．要将直径为d 的圆木锯成强度最大的横梁，断面的宽x 应为( )A.d 3B.d 2C.33d D.22d5．设x 0是函数f (x )＝12(e x ＋e －x )的最小值点，则曲线上点(x 0，f (x 0))处的切线方程是________． 6．已知函数f (x )＝x 3－12x ＋8在区间[－3,3]上的最大值与最小值分别为M ，m ，则M －m ＝________.7．求函数f (x )＝e x (3－x 2)在区间[2,5]上的最值．8．(江苏高考)请你设计一个包装盒．如图所示，ABCD 是边长为60 cm 的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A ，B ，C ，D 四个点重合于图中的点P ，正好形成一个正四棱柱形状的包装盒．E ，F 在AB 上，是被切去的一个等腰直角三角形斜边的两个端点．设AE ＝FB ＝x (cm)．(1)若广告商要求包装盒的侧面积S (cm 2)最大，试问：x 应取何值？(2)某厂商要求包装盒的容积V (cm 3)最大，试问：x 应取何值？并求出此时包装盒的高与底面边长的比值．答 案1．选A2．选B f ′(x )＝3x 2－2x －1，令f ′(x )＝0，解得x ＝－13(舍去)或x ＝1， 又f (0)＝a ，f (1)＝a －1，f (2)＝a ＋2，则f (2)最大，即a ＋2＝3，所以a ＝1.3．选A f ′(x )＝12e x (sin x ＋cos x )＋12e x (cos x －sin x )＝e x cos x ， 当0≤x ≤π2时，f ′(x )≥0， ∴f (x )在⎣⎢⎡⎦⎥⎤0，π2上是增函数． ∴f (x )的最大值为f ⎝ ⎛⎭⎪⎫π2＝12e π2， f (x )的最小值为f (0)＝12. 4．选C 设断面高为h ，则h 2＝d 2－x 2.设横梁的强度函数为f (x )，则f (x )＝k ·xh 2＝k ·x (d 2－x 2)，0<x <d .令f ′(x )＝k (d 2－3x 2)＝0，解得x ＝±33d (舍去负值)．当0<x <33d 时，f ′(x )>0，f (x )单调递增；当33d <x <d 时，f ′(x )<0，f (x )单调递减．所以函数f (x )在定义域(0，d )内只有一个极大值点x ＝33d .所以x ＝33d 时，f (x )有最大值，故选C.5．解析：f ′(x )＝12(e x －e －x )，令f ′(x )＝0，∴x ＝0， 可知x 0＝0为最小值点．切点为(0,1)，f ′(0)＝0为切线斜率，∴切线方程为y ＝1.答案：y ＝16．解析：令f ′(x )＝3x 2－12＝0，解得x ＝±2.计算f (－3)＝17，f (－2)＝24，f (2)＝－8，f (3)＝－1，所以M ＝24，m ＝－8，故M －m ＝32.答案：327．解：∵f (x )＝3e x －e x x 2，∴f ′(x )＝3e x －(e x x 2＋2e x x )＝－e x (x 2＋2x －3)＝－e x (x ＋3)(x －1)， ∵在区间[2,5]上，f ′(x )＝－e x (x ＋3)(x －1)<0，即函数f (x )在区间[2,5]上单调递减，∴x ＝2时，函数f (x )取得最大值f (2)＝－e 2；x ＝5时，函数f (x )取得最小值f (5)＝－22e 5.8．解：设包装盒的高为h (cm)，底面边长为a (cm)．由已知得a ＝2x ，h ＝60－2x 2＝2(30－x )，0＜x ＜30.(1)S ＝4ah ＝8x (30－x )＝－8(x －15)2＋1 800，所以当x ＝15时，S 取得最大值．(2)V ＝a 2h ＝22(－x 3＋30x 2)，V ′＝62x (20－x )．由V ′＝0得x ＝0(舍去)或x ＝20.当x ∈(0,20)时，V ′＞0；当x ∈(20,30)时，V ′＜0.所以当x ＝20时，V 取得极大值，也是最大值． 此时h a ＝12，即包装盒的高与底面边长的比值为12.。

课时跟踪检测（四）全集与补集层级一学业水平达标1．设集合U＝{1,2,3,4,5}，A＝{1,2}，B＝{2,3,4}，则∁U(A∪B)等于( )A．{2} B．{5}C．{1,2,3,4} D．{1,3,4,5}解析：选B∵A＝{1,2}，B＝{2,3,4}，∴A∪B＝{1,2,3,4}．又U＝{1,2,3,4,5}，∴∁U(A∪B)＝{5}．2．已知集合A＝{x∈R|－2＜x＜6}，B＝{x∈R|x＜2}，则A∪(∁R B)＝( )A．{x|x＜6} B．{x|－2＜x＜2}C．{x|x＞－2} D．{x|2≤x＜6}解析：选C由B＝{x∈R|x＜2}，得∁R B＝{x|x≥2}．又A＝{x∈R|－2＜x＜6}，所以A∪(∁R B)＝{x|x＞－2}．3．若P＝{x|x＜1}，Q＝{x|x＞－1}，则( )A．P⊆Q B．Q⊆PC．∁R P⊆Q D．Q⊆∁R P解析：选C∵P＝{x|x＜1}，∴∁R P＝{x|x≥1}，又Q＝{x|x＞－1}，∴∁R P⊆Q.4．已知全集U＝{1,2,3,4,5,6,7}，A＝{3,4,5}，B＝{1,3,6}，那么集合{2,7}是( )A．A∪B B．A∩BC．∁U(A∩B) D．∁U(A∪B)解析：选D∵A＝{3,4,5}，B＝{1,3,6}∴A∪B＝{1,3,4,5,6}又U＝{1,2,3,4,5,6,7}∴∁U(A∪B)＝{2,7}．5．已知A＝{x|x＋1＞0}，B＝{－2，－1,0,1}，则(∁R A)∩B＝( )A．{－2，－1} B．{－2}C．{－1,0,1} D．{0,1}解析：选A因为A＝{x|x＞－1}，所以∁R A＝{x|x≤－1}，所以(∁R A)∩B＝{－2，－1}．6．设全集为U，用集合A，B的交集、并集、补集符号表示图中的阴影部分．(1)________；(2)________．答案：(1)∁U(A∪B) (2)(∁U A)∩B7．已知全集U＝{x|x≥－3}，集合A＝{x|－3＜x≤4}，则∁U A＝________.解析：借助图形可知∁U A＝{x|x＝－3或x＞4}．答案：{x|x＝－3或x＞4}8．已知全集U＝{2,3，a2－a－1}，A＝{2,3}，若∁U A＝{1}，则实数a的值是________．解析：∵U＝{2,3，a2－a－1}，A＝{2,3}，∁U A＝{1}，∴a2－a－1＝1，即a2－a－2＝0，∴a＝－1或a＝2.答案：－1或29．已知集合A＝{x|－2＜x＜3}，B＝{x|m＜x＜m＋9}，若(∁R A)∩B＝B.求实数m的取值范围．解：∁R A＝{x|x≤－2，或x≥3}，由(∁R A)∩B＝B，得B⊆∁R A，∴m＋9≤－2，或m≥3.故m 的取值范围是{m|m≤－11，或m≥3}．10．已知全集U＝{x|x≤4}，集合A＝{x|－2＜x＜3}，B＝{x|－3≤x≤2}，求A∩B，∁A∪B，A∩∁U B，∁U(A∪B)．U解：如图所示．∵A＝{x|－2＜x＜3}，B＝{x|－3≤x≤2}，U＝{x|x≤4}，∴∁U A＝{x|x≤－2，或3≤x≤4}，∁U B＝{x|x＜－3，或2＜x≤4}，A∪B＝{x|－3≤x＜3}．∴A∩B＝{x|－2＜x≤2}，(∁U A)∪B＝{x|x≤2，或3≤x≤4}，A∩(∁B)＝{x|2＜x＜3}，∁U(A∪B)＝{x|x＜－3，或3≤x≤4}．U层级二应试能力达标1．设全集U＝M∪N＝{1,2,3,4,5}，M∩(∁U N)＝{2,4}，则N＝( )A．{1,2,3} B．{1,3,5}C．{1,4,5} D．{2,3,4}解析：选B由M∩(∁U N)＝{2,4}，可得集合N中不含元素2,4，集合M中含有元素2,4，故N ＝{1,3,5}．2.已知全集U＝Z，集合A＝{0,1}，B＝{－1,0,1,2}，则图中阴影部分所表示的集合为( )A．{－1,2} B．{－1,0}C．{0,1} D．{1,2}解析：选A图中阴影部分表示的集合为(∁U A)∩B，因为A＝{0,1}，B＝{－1,0,1,2}，所以(∁U A)∩B ＝{－1,2}．3．设S为全集，则下列几种说法中，错误的个数是( )①若A∩B＝∅，则(∁S A)∪(∁S B)＝S；②若A∪B＝S，则(∁S A)∩(∁S B)＝∅；③若A∪B＝∅，则A＝B.A．0 B．1C．2 D．3解析：选A①如图，(∁S A)∪(∁S B)＝S，正确．②若A∪B＝S，则(∁S A)∩(∁S B)＝∁S(A∪B)＝∅，正确．③若A∪B＝∅，则A＝B＝∅，正确．4．已知M，N为集合I的非空真子集，且M，N不相等，若N∩(∁I M)＝∅，则M∪N等于( )A ．MB ．NC ．ID ．∅解析：选A 根据题意画出Venn 图，由图可知M ∪N ＝M .5．设全集U 是实数集R ，M ＝{x |x ＜－2，或x ＞2}，N ＝{x |1≤x ≤3}，如图所示，则阴影部分所表示的集合为________．解析：∵M ＝{x |x ＜－2，或x ＞2}，N ＝{x |1≤x ≤3}， ∴M ∪N ＝{x |x ＜－2，或x ≥1}． ∴阴影部分所表示的集合为 ∁U (M ∪N )＝{x |－2≤x ＜1}． 答案：{x |－2≤x ＜1}6．某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为________人．解析：设两项运动都喜欢的人数为x ，画出Venn 图得到方程15－x ＋x ＋10－x ＋8＝30⇒x ＝3，∴喜爱篮球运动但不爱乒乓球运动的人数为15－3＝12(人)．答案：127．已知集合A ＝{x |x 2＋ax ＋12b ＝0}和B ＝{x |x 2－ax ＋b ＝0}，满足(∁R A )∩B ＝{2}，A ∩(∁R B )＝{4}，求实数a ，b 的值．解：由条件(∁R A )∩B ＝{2}和A ∩(∁R B )＝{4}，知2∈B ，但2∉A ；4∈A ，但4∉B .将x ＝2和x ＝4分别代入B ，A 两集合中的方程得⎩⎪⎨⎪⎧ 22－2a ＋b ＝0，42＋4a ＋12b ＝0，即⎩⎪⎨⎪⎧4－2a ＋b ＝0，4＋a ＋3b ＝0.解得a ＝87，b ＝－127即为所求．8．设全集是实数集R ，A ＝⎩⎨⎧⎭⎬⎫x 12≤x ≤3，B ＝{x |x 2＋a ＜0}．(1)当a ＝－4时，求A ∩B 和A ∪B ； (2)若(∁R A )∩B ＝B ，求实数a 的取值范围．解：(1)∵A ＝⎩⎨⎧⎭⎬⎫x 12≤x ≤3，当a ＝－4时，B ＝{x |－2＜x ＜2}，∴A ∩B ＝⎩⎨⎧⎭⎬⎫x 12≤x ＜2，A ∪B ＝{x |－2＜x ≤3}．(2)∁R A ＝⎩⎨⎧⎭⎬⎫xx ＜12，或x ＞3，当(∁R A )∩B ＝B 时，B ⊆∁R A .当B ＝∅，即a ≥0时，满足B ⊆∁R A ；当B ≠∅，即a ＜0时，B ＝{x |－－a ＜x ＜－a }．要使B ⊆∁R A ，需要－a ≤12，解得－14≤a ＜0.综上可得，实数a 的取值范围是⎣⎡⎭⎫－14，＋∞.。

课时跟踪检测（十八） 基本不等式与最大(小)值层级一 学业水平达标1．已知a ≥0，b ≥0，且a ＋b ＝2，则( )A ．ab ≤12B ．ab ≥12C ．a 2＋b 2≥2D ．a 2＋b 2≤2解析：选C 由a ＋b ＝2，得ab ≤⎝⎛⎭⎫a ＋b 22＝1，排除A 、B ；又a 2＋b 22≥⎝⎛⎭⎫a ＋b 22，∴a 2＋b 2≥2.故选C.2．若a ＞1，则a ＋1a －1的最小值是( ) A ．2B ．a C.2a a －1 D ．3解析：选D a ＞1，∴a －1＞0，∴a ＋1a －1＝a －1＋1a －1＋1≥2 (a －1)·1a －1＋1＝3，当且仅当a －1＝1a －1，即a ＝2时取等号． 3．已知x ＞1，y ＞1且lg x ＋lg y ＝4，那么lg x ·lg y 的最大值是( )A ．2B.12C.14D ．4 解析：选D ∵x ＞1，y ＞1，∴lg x ＞0，lg y ＞0，∴lg x ·lg y ≤⎝⎛⎭⎫lg x ＋lg y 22＝⎝⎛⎭⎫422＝4，当且仅当lg x ＝lg y ＝2，即x ＝y ＝100时成立等号成立．4．下列函数中，最小值为4的函数是( )A ．y ＝x ＋4xB ．y ＝sin x ＋4sin x (0＜x ＜π)C ．y ＝e x ＋4e －xD ．y ＝log 3x ＋log x 81解析：选C 对于A ，x ＋4x ≥4或者x ＋4x ≤－4；对于B ，等号成立的条件不满足；对于D ，也是log 3x ＋log x 81≥4或者log 3x ＋log x 81≤－4，故选C.5．某车间分批生产某种产品，每批的生产准备费用为800元．若每批生产x 件，则平均仓储时间为x 8天，且每件产品每天的仓储费用为1元．为使平均到每件产品的生产准备费用与仓储费用之和最小，每批应生产产品( )A. 60件B ．80件C ．100件D ．120件解析：选B 若每批生产x 件产品，则每件产品的生产准备费用是800x ，存储费用是x 8，总的费用是800x ＋x 8≥2 800x ·x 8＝20，当且仅当800x ＝x 8时取等号，得x ＝80. 所以每批应生产产品80件，才能使平均每件产品的生产准备费用与仓储费用之和最小．6．函数y ＝3x 2＋6x 2＋1的最小值是________． 解析：3x 2＋6x 2＋1＝3(x 2＋1)＋6x 2＋1－3≥62－3. 当且仅当3(x 2＋1)＝6x 2＋1时取等号． 答案：62－37．若log m n ＝－1，则3n ＋m 的最小值是________．解析：∵log m n ＝－1，∴mn ＝1且m >0，n >0，m ≠1.∴3n ＋m ≥23mn ＝2 3.当且仅当3n ＝m 即n ＝33，m ＝3时等号成立． 答案：2 38．函数y ＝log 2x ＋log x (2x )的值域是________．解析：y ＝log 2x ＋log x 2＋1.由|log 2x ＋log x 2|＝|log 2x |＋|log x 2|≥2|log 2x |·|log x 2|＝2，得log 2x ＋log x 2≥2或log 2x ＋log x 2≤－2，∴y ≥3或y ≤－1.答案：(－∞ ，－1]∪ [3，＋∞ )9．已知正常数a ，b 和正变数x ，y ，满足a ＋b ＝10，a x ＋b y ＝1，x ＋y 的最小值是18，求a ，b 的值．解：x ＋y ＝(x ＋y )⎝⎛⎭⎫a x ＋b y ＝a ＋b ＋bx y ＋ay x≥a ＋b ＋2ab ＝(a ＋b )2，∴(a ＋b )2＝18.又∵a ＋b ＝10，∴a ＝2，b ＝8或a ＝8，b ＝2.10．某单位决定投资3 200元建一仓库(长方体状)，高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米长造价45元，顶部每平方米造价20元，求：(1)仓库面积S 的最大允许值是多少？(2)为使S 达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？解：(1)设铁栅长为x 米，一堵砖墙长为y 米，而顶部面积为S ＝xy ，依题意得，40x ＋2×45y ＋20xy ＝3 200，由基本不等式得3 200≥240x ×90y ＋20xy＝120xy ＋20xy ，＝120S ＋20S .所以S ＋6S －160≤0，即(S －10)(S ＋16)≤0， 故S ≤10，从而S ≤100，所以S 的最大允许值是100平方米，(2)取得最大值的条件是40x ＝90y 且xy ＝100，求得x ＝15，即铁栅的长是15米．层级二 应试能力达标1．已知点P (x ，y )在经过A (3,0)，B (1,1)两点的直线上，则2x ＋4y 的最小值为( )A ．22B ．4 2C ．16D ．不存在解析：选B ∵点P (x ，y )在直线AB 上，∴x ＋2y ＝3.∴2x ＋4y ≥22x ·4y ＝22x ＋2y ＝42x ＝32，y ＝34时取等号． 2．已知x >0，y >0，x ＋2y ＋2xy ＝8，则x ＋2y 的最小值是( )A. 3B. 4C.92D.112解析：选B 依题意得(x ＋1)(2y ＋1)＝9，(x ＋1)＋(2y ＋1)≥2(x ＋1)(2y ＋1)＝6，即x ＋2y ≥4，当且仅当x ＋1＝2y ＋1，即x ＝2，y ＝1时取等号，故x ＋2y 的最小值是4.3．y ＝(3－a )(a ＋6)(－6≤a ≤3)的最大值为( )A ．9B.92 C ．3 D.322解析：选B 法一：因为－6≤a ≤3，所以3－a ≥0，a ＋6≥0，则由基本不等式可知，(3－a )(a ＋6)≤(3－a )＋(a ＋6)2＝92，当且仅当a ＝－32时等号成立． 法二：(3－a )(a ＋6)＝ －⎝⎛⎭⎫a ＋322＋814≤92，当且仅当a ＝－32时等号成立． 4．已知x >0，y >0，x ，a ，b ，y 成等差数列，x ，c ，d ，y 成等比数列，则(a ＋b )2cd 的最小值是( )A ．0B ．1C ．2D ．4解析：选D 因为x ，a ，b ，y 成等差数列，所以a ＋b ＝x ＋y .因为x ，c ，d ，y 成等比数列，所以cd ＝xy ，所以(a ＋b )2cd ＝(x ＋y )2xy ＝x 2＋y 2＋2xy xy ＝x 2＋y 2xy ＋2.因为x >0，y >0，所以x 2＋y 2xy＋2≥2xy xy＋2＝4，当且仅当x ＝y 时，等号成立． 5．建造一个容积为8 m 3，深为2 m 的长方体无盖水池，如果池底和池壁的造价分别为每平方米120元和80元，那么水池的最低总造价为__________元．解析：设水池池底的一边长为 x m ，则另一边长为4x m ，则总造价为：y ＝480＋80×⎝⎛⎭⎫2x ＋2×4x ×2＝480＋320⎝⎛⎭⎫x ＋4x ≥480＋320×2x ×4x ＝1 760. 当且仅当x ＝4x 即x ＝2时，y 取最小值1 760.所以水池的最低总造价为1 760元．答案：1 760 6．已知不等式(x ＋y )⎝⎛⎭⎫1x ＋a y ≥9对任意正实数x ，y 恒成立，则正实数a 的值为________． 解析：∵a >0，∴(x ＋y )⎝⎛⎭⎫1x ＋a y ＝1＋a ＋y x ＋xa y ≥1＋a ＋2a ，由条件知a ＋2a ＋1＝9，∴a ＝4.答案： 47．当x <32时，求函数y ＝x ＋82x －3的最大值． 解：y ＝12(2x －3)＋82x －3＋32＝－⎝⎛⎭⎪⎫3－2x 2＋83－2x ＋32， ∵当x <32时，3－2x >0， ∴3－2x 2＋83－2x ≥23－2x 2·83－2x ＝4，当且仅当3－2x 2＝83－2x，即x ＝－12时取等号． 于是y ≤－4＋32＝－52，故函数y 有最大值－52.8．北京市有关部门经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量y (千辆/小时)与汽车的平均速度v (千米/小时)之间的函数关系为y ＝920v v 2＋3v ＋1 600(v ＞0)． (1)在该时段内，当汽车的平均速度v 为多少时，车流量最大？最大车流量为多少？(精确到0.1千辆/小时)(2)若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？ 解：(1)由题意y ＝920v v 2＋3v ＋1 600＝920⎝⎛⎭⎫v ＋1 600v ＋3 ≤9202v ·1 600v＋3＝92083， 当且仅当v ＝1 600v ，即v ＝40时取等号． ∴y max ＝92083≈11.1(千辆/小时)， ∴当车速v ＝40千米/小时时，车流量最大为11.1千辆/小时．(2)由题意：920v v 2＋3v ＋1 600＞10， 整理得v 2－89v ＋1 600＜0，即(v －25)(v －64)＜0，解得25＜v ＜64.∴当车辆平均速度大于25千米/小时且小于64千米/小时时，车流量超过10千辆/小时．。

课时跟踪检测（十三）解三角形的实际应用举例层级一学业水平达标1.如图，两座灯塔A和B与海岸观察站C的距离相等，灯塔A在观察站南偏西40°,灯塔B在观察站南偏东60°，则灯塔A在灯塔B的（）A．北偏东10°B．北偏西10°C．南偏东80° D．南偏西80°解析：选D 由条件及题图可知，∠A＝∠B＝40°，又∠BCD ＝60°，所以∠CBD＝30°，所以∠DBA＝10°，因此灯塔A在灯塔B南偏西80°.2．甲、乙两人在同一地平面上的不同方向观测20 m高的旗杆，甲观测的仰角为50° ，乙观测的仰角为40° ，用d1，d2分别表示甲、乙两人离旗杆的距离，那么有（）A．d1＞d2B．d1＜d2C．d1＞20 m D．d2＜20 m解析：选B 由tan 50°＝错误!，tan 40°＝错误!及tan 50°＞tan 40°可知，d1＜d2。

3．一艘船以4 km/h的速度与水流方向成120°的方向航行，已知河水流速为2 km/h，则经过 3 h，则船实际航程为( )A．215 km B．6 kmC．2错误!km D．8 km解析：选B 如图所示，在△ACD中，AC＝2错误!,CD＝4错误!，∠ACD＝60°，∴AD2＝12＋48－2×23×43×错误!＝36.∴AD＝6。

即该船实际航程为6 km。

4．从高出海平面h米的小岛看正东方向有一只船俯角为30°，看正南方向一只船俯角为45°，则此时两船间的距离为( ）A．2h米B。

错误!h米C.3h米D．22h米解析：选A 如图所示，BC＝错误!h,AC＝h，∴AB＝错误!＝2h。

5．在200米高的山顶上，测得山下一塔顶与塔底的俯角分别为30°，60°，则塔高为( )A.错误!米B.错误!米C．200错误!米D．200米解析:选A 如图，设AB 为山高，CD 为塔高,则AB ＝200，∠ADM ＝30°，∠ACB ＝60°∴BC ＝错误!＝错误!，AM ＝DM tan 30°＝BC tan 30°＝错误!,∴CD ＝AB －AM ＝错误!。

北师大版2017-2018学年高中数学选修2-3全册课时跟踪训练目录课时跟踪训练(一) 分类加法计数原理和分步乘法计数原理1 课时跟踪训练(二)排列与排列数公式 (4)课时跟踪训练(三)排列的应用 (7)课时跟踪训练(四)组合与组合数公式 (10)课时跟踪训练(五)组合的应用 (13)课时跟踪训练(六)简单计数问题 (16)课时跟踪训练(七)二项式定理 (19)课时跟踪训练(八)二项式系数的性质 (22)课时跟踪训练(九)离散型随机变量及其分布列 (25)课时跟踪训练(十)超几何分布 (28)课时跟踪训练(十一)条件概率与独立事件 (31)课时跟踪训练(十二)二项分布 (35)课时跟踪训练(十三)离散型随机变量的均值 (39)课时跟踪训练(十四)离散型随机变量的方差 (44)课时跟踪训练(十五)正态分布 (48)阶段质量检测（一） (51)阶段质量检测（二） (56)阶段质量检测（三） (64)阶段质量检测(一) 计数原理 (72)阶段质量检测(二) 概率 (78)阶段质量检测(三) 统计案例 (86)阶段质量检测(四) 模块综合检测 (94)课时跟踪训练(一) 分类加法计数原理和分步乘法计数原理1．一个三层书架，分别放置语文书12本，数学书14本，英语书11本，从中任取一本，则不同的取法共有( )A ．37种B ．1 848种C ．3种D ．6种2．从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a ，b 组成复数a ＋b i ，其中虚数有( )A ．30个B ．42个C ．36个D ．35个3．现有高一学生9人，高二学生12人，高三学生7人，自发组织参加数学课外活动小组，从中推选两名来自不同年级的学生做一次活动的主持人，不同的选法共有( )A ．756种B ．56种C ．28种D ．255种4.用4种不同的颜色给矩形A ，B ，C ，D 涂色，要求相邻的矩形涂不同的颜色，则不同的涂色方法共有( )A ．12种B ．24种C ．48种D ．72种5．为了对某农作物新品种选择最佳生产条件，在分别有3种不同土质，2种不同施肥量，4种不同的种植密度，3种不同的种植时间的因素下进行种植试验，则不同的实验方案共有________种．6．如图，A →C ，有________种不同走法．7．设椭圆x 2a 2＋y 2b 2＝1，其中a ，b ∈{1,2,3,4,5}．(1)求满足条件的椭圆的个数；(2)如果椭圆的焦点在x 轴上，求椭圆的个数．8．某艺术小组有9人，每人至少会钢琴和小号中的1种乐器，其中7人会钢琴，3人会小号，从中选出会钢琴和会小号的各1人，有多少种不同的选法？答案1．选A根据分类加法计数原理，得不同的取法为N＝12＋14＋11＝37(种)．2．选C完成这件事分为两个步骤：第一步，虚部b有6种选法；第二步，实部a有6种选法．由分步乘法计数原理知，共有虚数6×6＝36 个．3．选D推选两名来自不同年级的两名学生，有N＝9×12＋12×7＋9×7＝255(种)．4．选D先涂C，有4种涂法，涂D有3种涂法，涂A有3种涂法，涂B有2种涂法．由分步乘法计数原理，共有4×3×3×2＝72种涂法．5．解析：根据分步乘法计数原理，不同的方案有N＝3×2×4×3＝72(种)．答案：726．解析：A→C的走法可分两类：第一类：A→C，有2种不同走法；第二类：A→B→C，有2×2＝4种不同走法．根据分类加法计数原理，得共有2＋4＝6种不同走法．答案：67．解：(1)由椭圆的标准方程知a≠b，要确定一个椭圆，只要把a，b一一确定下来这个椭圆就确定了．∴要确定一个椭圆共分两步：第一步确定a，有5种方法；第二步确定b，有4种方法，共有5×4＝20个椭圆．(2)要使焦点在x轴上，必须a>b，故可以分类：a＝2,3,4,5时，b的取值列表如下：故共有1＋2＋38．解：由题意可知，在艺术小组9人中，有且仅有1人既会钢琴又会小号(把该人称为“多面手”)，只会钢琴的有6人，只会小号的有2人，把选出会钢琴、小号各1人的方法分为两类：第一类：多面手入选，另1人只需从其他8人中任选一个，故这类选法共有8种．第二类：多面手不入选，则会钢琴者只能从6个只会钢琴的人中选出，会小号者也只能从只会小号的2人中选出，故这类选法共有6×2＝12种．因此有N＝8＋12＝20种不同的选法．课时跟踪训练(二) 排列与排列数公式1．5A 35＋4A 24等于( )A ．107B ．323C ．320D ．3482.A 345！等于( ) A.120 B.125 C.15D.1103．设a ∈N ＋，且a <27，则(27－a )(28－a )·…·(34－a )等于( ) A ．A 827－a B ．A 27－a34－aC ．A 734－aD ．A 834－a4．若从4名志愿者中选出2人分别从事翻译、导游两项不同工作，则选派方案共有( ) A ．16种 B ．6种 C ．15种D ．12种5．已知9！＝362 880，那么A 79＝________. 6．给出下列问题：①从1,3,5,7这四个数字中任取两数相乘，可得多少个不同的积？ ②从2,4,6,7这四个数字中任取两数相除，可得多少个不同的商？③有三种不同的蔬菜品种，分别种植在三块不同的试验田里，有多少种不同的种植方法？④有个头均不相同的五位同学，从中任选三位同学按左高右低的顺序并排站在一排照相，有多少种不同的站法？上述问题中，是排列问题的是________．(填序号)7．(1)计算4A 48＋2A 58A 88－A 59；(2)解方程3A x 8＝4A x －19.8．从语文、数学、英语、物理4本书中任意取出3本分给甲、乙、丙三人，每人一本，试将所有不同的分法列举出来．答案1．选D 原式＝5×5×4×3＋4×4×3＝348. 2．选C A 345！＝4×3×25×4×3×2×1＝15.3．选D 8个括号里面是连续的自然数，依据排列数的概念，选D.4．选D 4名志愿者分别记作甲、乙、丙、丁，则选派方案有：甲乙，甲丙，甲丁，乙甲，乙丙，乙丁，丙甲，丙乙，丙丁，丁甲，丁乙，丁丙，即共有A 24＝12种方案．5．解析：A 79＝9！(9－7)！＝362 8802＝181 440. 答案：181 4406．解析：对于①，任取两数相乘，无顺序之分，不是排列问题；对于②，取出的两数，哪一个作除数，哪一个作被除数，其结果不同，与顺序有关，是排列问题；对于③，三种不同的蔬菜品种任一种种植在不同的试验田里，结果不同，是排列问题；对于④，选出的三位同学所站的位置已经确定，不是排列问题．答案：②③7．解：(1)原式＝4A 48＋2×4A 484×3×2A 48－9A 48＝4＋824－9＝1215＝45. (2)由3A x 8＝4A x －19，得3×8！(8－x )！＝4×9！(10－x )！，化简，得x 2－19x ＋78＝0，解得x 1＝6，x 2＝13. 又∵x ≤8，且x －1≤9，∴原方程的解是x ＝6.8．解：从语文、数学、英语、物理4本书中任意取出3本，分给甲、乙、丙三人，每人一本，相当于从4个不同的元素中任意取出3个元素，按“甲、乙、丙”的顺序进行排列，每一个排列就对应着一种分法，所以共有A 34＝4×3×2＝24种不同的分法．不妨给“语文、数学、英语、物理”编号，依次为1,2,3,4号，画出下列树形图：由树形图可知，按甲乙丙的顺序分的分法为：语数英语数物语英数语英物语物数语物英数语英数语物数英语数英物数物语数物英英语数英语物英数语英数物英物语英物数物语数物语英物数语物数英物英语物英数课时跟踪训练(三)排列的应用1．6个人站成一排，甲、乙、丙3人必须站在一起的所有排列的总数为()A．A66B．3A33C．A33·A33D．A44·A332．(北京高考)从0,2中选一个数字，从1,3,5中选两个数字，组成无重复数字的三位数，其中奇数的个数为()A．24 B．18C．12 D．63．由数字1,2,3,4,5组成的所有没有重复数字的5位数中，大于23 145且小于43 521的数共有()A．56个B．57个C．58个D．60个4．(辽宁高考)6把椅子摆成一排，3人随机就座，任何两人不相邻的坐法种数为() A．144 B．120C．72 D．245．(大纲全国卷)6个人排成一行，其中甲、乙两人不相邻的不同排法共有________种．(用数字作答)6．有A，B，C，D，E五位学生参加网页设计比赛，决出了第一到第五的名次，A，B 两位学生去问成绩，老师对A说：“你的名次不知道，但肯定没得第一名”；又对B说：“你是第三名”．请你分析一下，这五位学生的名次排列共有________种不同的可能．7．由A，B，C等7人担任班级的7个班委．(1)若正、副班长两职只能由这三人中选两人担任，有多少种分工方案？(2)若正、副班长两职至少要选三人中的1人担任，有多少种分工方案？8．如图，某伞厂生产的“太阳”牌太阳伞蓬是由太阳光的七种颜色组成的，七种颜色分别涂在伞蓬的八个区域内，且恰有一种颜色涂在相对区域内，则不同的颜色图案的此类太阳伞至多有多少种？答案1．选D甲、乙、丙3人站在一起有A33种站法，把3人作为一个元素与其他3人排列有A44种，共有A33·A44种．2．选B若选0，则0只能在十位，此时组成的奇数的个数是A23；若选2，则2只能在十位或百位，此时组成的奇数的个数是2×A23＝12，根据分类加法计数原理得总个数为6＋12＝18.3．选C首位为3时，有A44＝24个；首位为2时，千位为3，则有A12A22＋1＝5个，千位为4或5时有A12A33＝12个；首位为4时，千位为1或2有A12A33＝12个，千位为3时，有A12A22＋1＝5个．由分类加法计数原理知，共有符合条件的数字24＋5＋12＋12＋5＝58(个)．4．选D剩余的3个座位共有4个空隙供3人选择就座，因此任何两人不相邻的坐法种数为A34＝4×3×2＝24.5．解析：法一：先把除甲、乙外的4个人全排列，共有A44种方法．再把甲、乙两人插入这4人形成的五个空位中的两个，共有A25种不同的方法．故所有不同的排法共有A44·A25＝24×20＝480(种)．法二：6人排成一行，所有不同的排法有A66＝720(种)，其中甲、乙相邻的所有不同的排法有A55A22＝240(种)，所以甲、乙不相邻的不同排法共有720－240＝480(种)．答案：4806．解析：先安排B有1种方法，再安排A有3种方法，最后安排C，D，E共A33种方法．由分步乘法计数原理知共有3A33＝18种方法．答案：187．解：(1)先安排正、副班长有A23种方法，再安排其余职务有A55种方法，依分步乘法计数原理，共有A23A55＝720种分工方案．(2)7人的任意分工方案有A77种，A，B，C三人中无一人任正、副班长的分工方案有A24 A55种，因此A，B，C三人中至少有1人任正、副班长的方案有A77－A24A55＝3 600种．8.解：如图，对8个区域进行编号，任选一组对称区域(如1与5)同色，用7种颜色涂8个区域的不同涂法有7！种，又由于1与5,2与6,3与7,4与8是对称的，通过旋转后5,6,7,8,1,2,3,4与1,2,3,4,5,6,7,8是同一种涂色，即重复染色2次，故此种图案至多有7！2＝2 520种．课时跟踪训练(四)组合与组合数公式1．给出下面几个问题：①10人相互通一次电话，共通多少次电话？②从10个人中选出3个作为代表去开会，有多少种选法？③从10个人中选出3个不同学科的课代表，有多少种选法？④由1,2,3组成无重复数字的两位数．其中是组合问题的有()A．①③B．②④C．①②D．①②④2．若A3n＝12C2n，则n等于()A．8 B．5或6C．3或4 D．43．下列四个式子中正确的个数是()(1)C m n＝A m nm！；(2)A m n＝n A m－1n－1；(3)C m n÷C m＋1n ＝m＋1n－m；(4)C m＋1n＋1＝n＋1m＋1C m n.A．1个B．2个C．3个D．4个4．若C7n＋1－C7n＝C8n，则n等于()A．12 B．13C．14 D．155．从2,3,5,7四个数中任取两个不同的数相乘，有m个不同的积，任取两个不同的数相除，有n个不同的商，则m∶n＝________.6．方程C x28＝C3x－828的解为________．7．计算：(1)C58＋C98100C77；(2)C05＋C15＋C25＋C35＋C45＋C55.8．在一次数学竞赛中，某学校有12人通过了初试，学校要从中选出5人去参加市级培训，在下列条件下，有多少种不同的选法？(1)任意选5人；(2)甲、乙、丙三人必须参加； (3)甲、乙、丙三人不能参加； (4)甲、乙、丙三人只能有1人参加．答案1．选C ①是组合问题，因为甲与乙通了一次电话，也就是乙与甲通了一次电话，没有顺序的区别；②是组合问题，因为三个代表之间没有顺序的区别；③是排列问题，因为三个人担任哪一科的课代表是有顺序区别的；而④中选出的元素还需排列，有顺序问题是排列．所以①②是组合问题．2．选A ∵A 3n ＝12C 2n ，∴n (n －1)(n －2)＝12×n (n －1)2.解得n ＝8. 3．选D 因为C m n ＝n ！m ！(n －m )！＝1m ！·n ！(n －m )！＝A m nm ！，故(1)正确；因为n A m －1n －1＝n ·(n －1)！(n －m )！＝n ！(n －m )！＝A m n ，故(2)正确； 因为Cmn÷Cm ＋1n＝n ！m ！(n －m )÷n ！(m ＋1)！(n －m －1)！＝n ！m ！(n －m )！×(m ＋1)！(n －m －1)！n ！＝m ＋1n －m，故(3)正确．因为C m ＋1n ＋1＝(n ＋1)！(m ＋1)！(n －m )！，n ＋1m ＋1C m n ＝n ＋1m ＋1·n ！m ！(n －m )！＝(n ＋1)！(m ＋1)！(n －m )！，所以C m ＋1n ＋1＝n ＋1m ＋1C m n，故(4)正确． 4．选C C 7n ＋1－C 7n ＝C 8n ，即C 7n ＋1＝C 8n ＋C 7n ＝C 8n ＋1，所以n ＋1＝7＋8，即n ＝14.5．解析：∵m ＝C 24，n ＝A 24，∴m ∶n ＝12. 答案：126．解析：当x ＝3x －8，解得x ＝4；当28－x ＝3x －8，解得x ＝9. 答案：4或97．解：(1)原式＝C 38＋C 2100×1＝8×7×63×2×1＋100×992×1 ＝56＋4 950＝5 006.(2)原式＝2(C 05＋C 15＋C 25)＝2(C 16＋C 25)＝2×⎝ ⎛⎭⎪⎫6＋5×42×1＝32. 8．解：(1)C 512＝792种不同的选法．(2)甲、乙、丙三人必须参加，只需从另外的9人中选2人，共有C 29＝36种不同的选法． (3)甲、乙、丙三人不能参加，只需从另外的9人中选5人，共有C 59＝126种不同的选法．(4)甲、乙、丙三人只能有1人参加，分两步：第一步从甲、乙、丙中选1人，有C 13＝3种选法；第二步从另外的9人中选4人有C 49种选法．共有C 13C 49＝378种不同的选法．课时跟踪训练(五)组合的应用1．9件产品中，有4件一等品，3件二等品，2件三等品，现在要从中抽出4件产品，抽出产品中至少有2件一等品的抽法种数为()A．81B．60C．6 D．112．以一个正三棱柱的顶点为顶点的四面体有()A．6个B．12个C．18个D．30个3．从10名大学毕业生中选3个人担任村长助理，则甲、乙至少有1人入选，而丙没有入选的不同选法的种数为()A．85 B．56C．49 D．284．在某种信息传输过程中，用4个数字的一个排列(数字允许重复)表示一个信息，不同排列表示不同信息，若所用数字只有0和1，则与信息0110至多有两个对应位置上的数字相同的信息个数为()A．10 B．11C．12 D．155．(大纲全国卷)从进入决赛的6名选手中决出1名一等奖，2名二等奖，3名三等奖，则可能的决赛结果共有________种．(用数字作答)6．某校开设9门课程供学生选修，其中A，B，C三门由于上课时间相同，至多选一门．学校规定，每位同学选修4门，共有________种不同选修方案．(用数字作答) 7．12件产品中，有10件正品，2件次品，从这12件产品中任意抽出3件．(1)共有多少种不同的抽法？(2)抽出的3件中恰好有1件次品的抽法有多少种？(3)抽出的3件中至少有1件次品的抽法有多少种？8．10双互不相同的鞋子混装在一只口袋中，从中任意取出4只，试求各有多少种情况出现如下结果：(1)4只鞋子没有成双的；(2)4只鞋子恰成两双；(3)4只鞋中有2只成双，另2只不成双．答案1．选A分三类：恰有2件一等品，有C24C25＝60种取法；恰有3件一等品，有C34C15＝20种取法；恰有4件一等品，有C44＝1种取法．∴抽法种数为60＋20＋1＝81.2．选B从6个顶点中任取4个有C46＝15种取法，其中四点共面的有3种．所以满足题意的四面体有15－3＝12个．3．选C由条件可分为两类：一类是甲、乙两人只有一人入选，有C12·C27＝42种不同选法，另一类是甲、乙都入选，有C22·C17＝7种不同选法，所以共有42＋7＝49种不同选法．4．选B与信息0110至多有两个位置上的数字对应相同的信息包括三类：第一类：与信息0110只有两个对应位置上的数字相同有C24＝6个；第二类：与信息0110只有一个对应位置上的数字相同有C14＝4个；第三类：与信息0110没有一个对应位置上的数字相同有C04＝1个．∴与信息0110至多有两个对应位置上的数字相同的信息有6＋4＋1＝11个．5．解析：第一步决出一等奖1名有C16种情况，第二步决出二等奖2名有C25种情况，第三步决出三等奖3名有C33种情况，故可能的决赛结果共有C16C25C33＝60种情况．答案：606．解析：分两类完成：第一类，A，B，C三门课程都不选，有C46种不同的选修方案；第二类，A，B，C三门课程恰好选修一门，有C13·C36种不同选修方案．故共有C46＋C13·C36＝75种不同的选修方案．答案：757．解：(1)有C312＝220种抽法．(2)分两步：先从2件次品中抽出1件有C12种方法；再从10件正品中抽出2件有C210种方法，所以共有C12C210＝90种抽法．(3)法一(直接法)：分两类：即包括恰有1件次品和恰有2件次品两种情况，与(2)小题类似共有C12C210＋C22C110＝100种抽法．法二(间接法)：从12件产品中任意抽出3件有C312种方法，其中抽出的3件全是正品的抽法有C310种方法，所以共有C312－C310＝100种抽法．8．解：(1)从10双鞋子中选取4双，有C410种不同选法，每双鞋子中各取一只，分别有2种取法，根据分步乘法计数原理，选取种数为N＝C410·24＝3 360(种)．即4只鞋子没有成双有3 360种不同取法．(2)从10双鞋子中选取2双有C210种取法，所以选取种数为N＝C210＝45(种)，即4只鞋子恰成双有45种不同取法．(3)先选取一双有C110种选法，再从9双鞋中选取2双有C29种选法，每双鞋只取一只各有2种取法．根据分步乘法计数原理，不同取法为N＝C110C29·22＝1 440(种)．课时跟踪训练(六)简单计数问题1．从4名男生和3名女生中选3人分别从事三项不同的工作，若这3人中至少有1名女生，则选派的方案共有()A．108种B．186种C．216种D．270种2．12名同学合影，站成了前排4人后排8人，现摄影师要从后排8人中抽2人调整到前排，若其他人的相对顺序不变，则不同调整方法的种数是()A．C28A23B．C28A66C．C28A26D．C28A253．(大纲全国卷)将字母a，a，b，b，c，c排成三行两列，要求每行的字母互不相同，每列的字母也互不相同，则不同的排列方法共有()A．12种B．18种C．24种D．36种4．6个人分乘两辆不同的汽车，每辆车最多坐4人，则不同的乘车方法有() A．40种B．50种C．60种D．70种5．将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，则不同的放球方法有________种．6.要在如图所示的花圃中的5个区域中种入4种颜色不同的花，要求相邻区域不同色，有________种不同的种法．7．如图，在∠AOB的两边上，分别有3个点和4个点，连同角的顶点共8个点．这8个点能作多少个三角形？8．有9本不同的课外书，分给甲、乙、丙三名同学，求在下列条件下，各有多少种分法？(1)甲得4本，乙得3本，丙得2本；(2)一人得4本，一人得3本，一人得2本．答案1．选B(1)直接法：从4名男生和3名女生中选出3人，至少有1名女生的选派方案可分为三类：①恰好有1名女生，2名男生，有C13C24A33种方法；②恰好有2名女生，1名男生，有C23C14A33种方法；③恰好有3名女生，有C33A33种方法；由分类加法计数原理得共有C13 C24A33＋C23C14A33＋C33A33＝186种不同的选派方案．(2)间接法：从全部方案数中减去只派男生的方案数，则有A37－A34＝186种不同的选派方案．2．选C从后排8人中选2人安排到前排6个位置中的任意两个位置即可，所以选法种数是C28A26.3．选A由分步乘法计数原理，先排第一列，有A33种方法，再排第二列，有2种方法，故共有A33×2＝12种排列方法．4．选B先分组再排列，一组2人一组4人有C26＝15种不同的分法；两组各3人共有C36A22＝10种不同的分法，所以共有(15＋10)×2＝50种不同的乘车方法．5．解析：有两种满足题意的放法：(1)1号盒子里放2个球，2号盒子里放2个球，有C24C22种放法；(2)1号盒子里放1个球，2号盒子里放3个球，有C14C33种放法．综上可得，不同的放球方法共有C24C22＋C14C33＝10种．答案：106．解析：区域5有4种种法，区域1有3种种法，区域4有2种种法，若1,3同色，区域2有2种种法，或1,3不同色，区域2有1种种法，所以共有4×3×2×(1×2＋1×1)＝72种不同的种法．答案：727．解：从8个点中，任选3点共有C38种选法，其中有一个5点共线和4点共线，故共有C38－C34－C35＝42个不同的三角形．8．解：(1)分三步完成：第一步：从9本不同的书中，任取4本分给甲，有C49种方法；第二步：从余下的5本书中，任取3本给乙，有C35种方法；第三步：把剩下的书给丙，有C22种方法．∴共有不同的分法为C49C35C22＝1 260种．(2)分两步完成：第一步：按4本、3本、2本分成三组有C49C35C22种方法；第二步：将分成的三组书分给甲、乙、丙三个人，有A33种方法．∴共有C49C35C22A33＝7 560种．课时跟踪训练(七) 二项式定理1．(x －2y )7的展开式中的第4项为( ) A ．－280x 4y 3 B ．280x 4y 3 C ．－35x 4y 3D ．35x 4y 32．在(x －3)10的展开式中，x 6的系数是( ) A ．－27C 610B ．27C 410 C ．－9C 610D ．9C 4103．(大纲全国卷)(1＋x )8(1＋y )4的展开式中x 2y 2的系数是( ) A ．56 B ．84 C ．112D ．1684．已知⎝⎛⎭⎫2x 3＋1x n 的展开式中的常数项是第7项，则正整数n 的值为( ) A ．7 B ．8 C ．9D ．105．(安徽高考)若⎝ ⎛⎭⎪⎫x ＋a 3x 8的展开式中x 4的系数为7，则实数a ＝________. 6．(浙江高考)设二项式⎝ ⎛⎭⎪⎫x －13x 5的展开式中常数项为A ，则A ＝________.7.⎝⎛⎭⎪⎫x ＋23x n展开式第9项与第10项二项式系数相等，求x 的一次项系数．8．在⎝⎛⎭⎪⎫2x 2－13x 8的展开式中，求：(1)第5项的二项式系数及第5项的系数； (2)倒数第3项．答案1．选A (x －2y )7的展开式中的第4项为T 4＝C 37x 4(－2y )3＝(－2)3C 37x 4y 3＝－280x 4y 3. 2．选D T k ＋1＝C k 10·x 10－k (－3)k ，令10－k ＝6，知k ＝4，∴T 5＝C 410x 6(－3)4，即x 6的系数为9C 410.3．选D 在(1＋x )8展开式中含x 2的项为C 28x 2＝28x 2，(1＋y )4展开式中含y 2的项为C 24y2＝6y 2，所以x 2y 2的系数为28×6＝168，故选D.4．选B ⎝⎛⎭⎫2x 3＋1x n 的展开式的通项T r ＋1＝C r n 2n －r x 3n －4r，由r ＝6时，3n －4r ＝0.得n ＝8.5．解析：二项式⎝⎛⎭⎪⎫x ＋a 3x 8展开式的通项为T r ＋1＝C r 8a rx 8－43r ，令8－43r ＝4，可得r ＝3，故C 38a 3＝7，易得a ＝12. 答案：126．解析：T r ＋1＝(－1)r C r 5x 15－5r 6，令15－5r ＝0，得r ＝3，故常数项A ＝(－1)3C 35＝－10.答案：－107．解：由题意知，C 8n ＝C 9n .∴n ＝17.∴T r ＋1＝C r 17x 17－r 2·2r ·x －r 3＝C r 17·2r ·x 17－r 2－r 3. ∴17－r 2－r3＝1. 解得r ＝9.∴T r ＋1＝C 917·x 4·29·x －3， 即T 10＝C 917·29·x . 其一次项系数为C 917·29. 8．解：法一：利用二项式的展开式解决．(1)⎝ ⎛⎭⎪⎫2x 2－13x 8＝(2x 2)8－C 18(2x 2)7·13x＋C 28(2x 2)6·⎝ ⎛⎭⎪⎫13x 2－C 38(2x 2)5·⎝ ⎛⎭⎪⎫13x 3＋C 48(2x 2)4·⎝ ⎛⎭⎪⎫13x 4－C 58(2x 2)3·⎝ ⎛⎭⎪⎫13x 5＋C 68(2x 2)2·⎝ ⎛⎭⎪⎫13x 6－C 78(2x 2)·⎝ ⎛⎭⎪⎫13x 7＋C 88⎝ ⎛⎭⎪⎫13x 8，则第5项的二项式系数为C 48＝70，第5项的系数C 48·24＝1 120. (2)由(1)中⎝ ⎛⎭⎪⎫2x 2－13x 8的展开式可知倒数第3项为C 68·(2x 2)2·⎝ ⎛⎭⎪⎫13x 6＝112x 2. 法二：利用二项展开式的通项公式．(1)T 5＝C 48(2x 2)8－4·⎝⎛⎭⎪⎫－13x 4＝C 48·24·x 203， 则第5项的二项式系数是C 48＝70， 第5项的系数是C 48·24＝1 120. (2)展开式中的倒数第3项即为第7项， T 7＝C 68·(2x 2)8－6·⎝⎛⎭⎪⎫－13x 6＝112x 2.课时跟踪训练(八) 二项式系数的性质1．(x －1)11展开式中x 的偶次项系数之和是( ) A ．－2 048 B ．－1 023 C ．－1 024D ．1 0242．若C 1n x ＋C 2n x 2＋…＋C n n x n能被7整除，则x ，n 的值可能为( )A ．x ＝4，n ＝3B ．x ＝4，n ＝4C ．x ＝5，n ＝4D ．x ＝6，n ＝53．若⎝⎛⎫x ＋1x n 展开式的二项式系数之和为64，则展开式的常数项为( ) A ．10 B ．20 C ．30D ．1204．在⎝⎛⎭⎫ax －1x 4的展开式中各项系数之和是16.则a 的值是( ) A ．2 B ．3 C ．4D ．－1或35．若(x 2＋1)(2x ＋1)9＝a 0＋a 1(x ＋2)＋a 2(x ＋2)2＋…＋a 11(x ＋2)11，则a 0＋a 1＋a 2＋…＋a 11的值为________．6．若(2x ＋3)4＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4，则(a 0＋a 2＋a 4)2－(a 1＋a 3)2的值为________． 7．已知(1＋3x )n 的展开式中，末三项的二项式系数的和等于121，求展开式中二项式系数最大的项．8．对二项式(1－x )10，(1)展开式的中间项是第几项？写出这一项． (2)求展开式中各二项式系数之和．(3)求展开式中除常数项外，其余各项的系数和．答案1．选C 令f (x )＝(x －1)11，偶次项系数之和是f (1)＋f (－1)2＝(－2)112＝－1 024.2．选C 由C 1n x ＋C 2n x 2＋…＋C n n x n ＝(1＋x )n－1分别将选项A ，B ，C ，D 代入检验知，仅有x ＝5，n ＝4适合．3．选B 由2n ＝64，得n ＝6，∴T k ＋1＝C k 6x 6－k ⎝⎛⎭⎫1x k ＝C k 6x6－2k(0≤k ≤6，k ∈N )．由6－2k ＝0，得k ＝3.∴T 4＝C 36＝20.4．选D 由题意可得(a －1)4＝16，a －1＝±2， 解得a ＝－1或a ＝3.5．解析：令x ＝－1，则原式可化为[(－1)2＋1][2×(－1)＋1]9＝－2＝a 0＋a 1(2－1)＋…＋a 11(2－1)11，∴a 0＋a 1＋a 2＋…＋a 11＝－2.答案：－26．解析：(a 0＋a 2＋a 4)2－(a 1＋a 3)2＝(a 0＋a 2＋a 4＋a 1＋a 3)·(a 0＋a 2＋a 4－a 1－a 3)＝(a 0＋a 1＋a 2＋a 3＋a 4)·(a 0－a 1＋a 2－a 3＋a 4)，令x ＝1，则a 0＋a 1＋a 2＋a 3＋a 4＝(2＋3)4，令x ＝－1，则a 0－a 1＋a 2－a 3＋a 4＝(－2＋3)4＝(2－3)4，于是(2＋3)4·(2－3)4＝1.答案：17．解：由题意知C n n ＋C n －1n ＋C n －2n ＝121，即C 0n ＋C 1n ＋C 2n ＝121，∴1＋n ＋n (n －1)2＝121，即n 2＋n －240＝0，解得n ＝15或－16(舍)．∴在(1＋3x )15的展开式中二项式系数最大的项是第八、九两项．且T 8＝C 715(3x )7＝C 71537x 7， T 9＝C 815(3x )8＝C 81538x 8.8．解：(1)展开式共11项，中间项为第6项，T 6＝C 510(－x )5＝－252x 5. (2)C 010＋C 110＋C 210＋…＋C 1010＝210＝1 024.(3)设(1－x )10＝a 0＋a 1x ＋a 2x 2＋…＋a 10x 10. 令x ＝1，得a 0＋a 1＋a 2＋…＋a 10＝0. 令x ＝0，得a 0＝1.∴a1＋a2＋…＋a10＝－1.课时跟踪训练(九)离散型随机变量及其分布列1．一个袋子中有质量相等的红、黄、绿、白四种小球各若干个，一次倒出三个小球，下列变量是离散型随机变量的是()A．小球滚出的最大距离B．倒出小球所需的时间C．倒出的三个小球的质量之和D．倒出的三个小球的颜色种数2．袋中有大小相同的5个钢球，分别标有1,2,3,4,5五个号码．在有放回地抽取条件下依次取出2个球，设两个球号码之和为随机变量X，则X所有可能值的个数是() A．25B．10C．9 D．53．设随机变量X等可能取值1,2,3，…，n，若P(X<4)＝0.3，则n＝()A．3 B．4C．10 D．不确定4．设随机变量X等可能地取值1,2,3,4，…，10.又设随机变量Y＝2X－1，P(Y<6)的值为()A．0.3 B．0.5C．0.1 D．0.25．随机变量Y的分布列如下：则(1)x＝(3)P(1＜Y≤4)＝________.6．随机变量X的分布列为P(X＝k)＝Ck(k＋1)，k＝1,2,3，其中C为常数，则P(X≥2)＝________.7．若离散型随机变量X的分布列为：求常数a8．设S 是不等式x 2－x －6≤0的解集，整数m ，n ∈S .(1)记“使得m ＋n ＝0成立的有序数组(m ，n )”为事件A ，试列举A 包含的基本事件； (2)设X ＝m 2，求X 的分布列．答案1．选D A ，B 不能一一列举，不是离散型随机变量，而C 是常量，是个确定值，D 可能取1,2,3，是离散型随机变量．2．选C 第一次可取1,2,3,4,5中的任意一个，由于是有放回抽取，第二次也可取1,2,3,4,5中的任何一个，两次的号码和可能为2,3,4,5,6,7,8,9,10.3．选C ∵X 等可能取1,2,3，…，n ， ∴X 的每个值的概率均为1n.由题意知P (X <4)＝P (X ＝1)＋P (X ＝2)＋P (X ＝3)＝3n ＝0.3，∴n ＝10.4．选A Y <6，即2X －1<6，∴X <3.5.X ＝1,2,3，P ＝310.5．解析：(1)由 i ＝16p i ＝1，∴x ＝0.1.(2)P (Y ＞3)＝P (Y ＝4)＋P (Y ＝5)＋P (Y ＝6) ＝0.1＋0.15＋0.2＝0.45.(3)P (1＜Y ≤4)＝P (Y ＝2)＋P (Y ＝3)＋P (Y ＝4) ＝0.1＋0.35＋0.1＝0.55. 答案：(1)0.1 (2)0.45 (3)0.556．解析：由P (X ＝1)＋P (X ＝2)＋P (X ＝3)＝1，得C 1×2＋C 2×3＋C 3×4＝1，∴C ＝43.P (X ≥2)＝P (X ＝2)＋P (X ＝3)＝432×3＋433×4＝13.答案：137．解：由离散型随机变量的性质得 ⎩⎪⎨⎪⎧9a 2－a ＋3－8a ＝1，0≤9a 2－a ≤1，0≤3－8a ≤1，解得a ＝13，或a ＝23(舍)．所以随机变量X 的分布列为：8．解：(1)由x 2－x －6≤0，得－2≤x ≤3， 即S ＝{x |－2≤x ≤3}．由于m ，n ∈Z ，m ，n ∈S 且m ＋n ＝0，所以A 包含的基本事件为(－2,2)，(2，－2)，(－1,1)，(1，－1)，(0,0)．(2)由于m 的所有不同取值为－2，－1,0,1,2,3， 所以X ＝m 2的所有不同取值为0,1,4,9， 且有P (X ＝0)＝16，P (X ＝1)＝26＝13，P (X ＝4)＝26＝13，P (X ＝9)＝16.故X 的分布列为课时跟踪训练(十) 超几何分布1．一个小组有6人，任选2名代表，求其中甲当选的概率是( ) A.12 B.13 C.14D.152．在一个口袋中装有5个白球和3个黑球，这些球除颜色外完全相同，从中摸出3个球，至少摸到2个黑球的概率等于( )A.27 B.38 C.37D.9283．某12人的兴趣小组中，有5名“三好生”，现从中任意选6人参加竞赛，用X 表示这6人中“三好生”的人数，则C 35C 37C 612是表示的概率是( )A ．P (X ＝2)B ．P (X ＝3)C ．P (X ≤2)D ．P (X ≤3)4．从一副不含大、小王的52张扑克牌中任意抽出5张，则至少有3张A 的概率为( )A.C 34C 248C 552B.C 348C 24C 552C ．1－C 148C 44C 552D.C 34C 248＋C 44C 148C 5525．某小组共有10名学生，其中女生3名，现选举2名代表，至少有1名女生当选的概率为________．6．知识竞答，共有10个不同的题目，其中选择题6个，判断题4个，小张抽4题，则小张抽到选择题至少2道的概率为________．7．一盒中有12个乒乓球，其中9个新的，3个旧的，从盒中任取3个球来用，用完后装回盒中，此时盒中旧球个数X 是一个随机变量，求X 的分布列．8．在一次购物抽奖活动中，假设10张奖券中有一等奖奖券1张，可获价值50元的奖品，有二等奖奖券3张，每张可获价值10元的奖品，其余6张没有奖品．(1)顾客甲从10张奖券中任意抽取1张，求中奖次数X 的分布列． (2)顾客乙从10张奖券中任意抽取2张． ①求顾客乙中奖的概率；②设顾客乙获得的奖品总价值Y 元，求Y 的分布列．答案1．选B 设X 表示2名代表中有甲的个数，X 的可能取值为0,1， 由题意知X 服从超几何分布，其中参数为N ＝6，M ＝1，n ＝2，则P (X ＝1)＝C 11C 15C 26＝13.2．选A 黑球的个数X 服从超几何分布，则至少摸到2个黑球的概率P (X ≥2)＝P (X ＝2)＋P (X ＝3)＝C 23C 15C 38＋C 33C 05C 38＝27.3．选B 6人中“三好生”的人数X 服从超几何分布，其中参数为N ＝12，M ＝5，n＝6，所以P (X ＝3)＝C 35C 37C 612.4．选D 设X 为抽出的5张扑克牌中含A 的张数．则P (X ≥3)＝P (X ＝3)＋P (X ＝4)＝C 34C 248C 552＋C 44C 148C 552.5．解析：至少有1名女生当选包括1男1女，2女两种情况，概率为C 13C 17＋C 23C 210＝815. 答案：8156．解析：由题意知小张抽到选择题数X 服从超几何分布(N ＝10，M ＝6，n ＝4)， 小张抽到选择题至少2道的概率为：P (X ≥2)＝P (X ＝2)＋P (X ＝3)＋P (X ＝4)＝C 26C 24C 410＋C 36C 14C 410＋C 46C 04C 410＝3742.答案：37427．解：由题意知，旧球个数X 的所有可能取值为3,4,5,6.则P (X ＝3)＝C 33C 312＝1220，P (X ＝4)＝C 23C 19C 312＝27220，P (X ＝5)＝C 29C 13C 312＝108220＝2755，P (X ＝6)＝C 39C 312＝84220＝2155.所以X 的分布列为8．解：(1)抽奖一次，只有中奖和不中奖两种情况，故X 的取值只有0和1两种情况． P (X ＝1)＝C 14C 110＝410＝25，则P (X ＝0)＝1－P (X ＝1)＝1－25＝35.因此X 的分布列为(2)①顾客乙中奖可分为互斥的两类：所抽取的2张奖券中有1张中奖或2张都中奖．故所求概率P ＝C 14C 16＋C 24C 06C 210＝3045＝23. ②Y 的所有可能取值为0,10,20,50,60，且P (Y ＝0)＝C 04C 26C 210＝1545＝13，P (Y ＝10)＝C 13C 16C 210＝1845＝25，P (Y ＝20)＝C 23C 06C 210＝345＝115，P (Y ＝50)＝C 11C 16C 210＝645＝215，P (Y ＝60)＝C 11C 13C 210＝345＝115.因此随机变量Y 的分布列为课时跟踪训练(十一) 条件概率与独立事件1．抛掷一颗骰子一次，A 表示事件：“出现偶数点”，B 表示事件：“出现3点或6点”，则事件A 与B 的关系是( )A ．相互互斥事件B ．相互独立事件C ．既相互互斥又相互独立事件D ．既不互斥又不独立事件2．设A ，B 为两个事件，若事件A 和B 同时发生的概率为310，在事件A 发生的条件下，事件B 发生的概率为12，则事件A 发生的概率为( )A.25 B.35 C.45D.3103．某农业科技站对一批新水稻种子进行试验，已知这批水稻种子的发芽率为0.8，出芽后的幼苗成活率为0.9，在这批水稻种子中，随机地取出一粒，则这粒水稻种子发芽能成长为幼苗的概率为( )A ．0.02B ．0.08C ．0.18D ．0.724．从某地区的儿童中挑选体操学员，已知儿童体型合格的概率为15，身体关节构造合格的概率为14，从中任挑一儿童，这两项至少有一项合格的概率是(假定体型与身体关节构造合格与否相互之间没有影响)( )A.1320B.15C.14D.255．有一个数学难题，在半小时内，甲能解决的概率是12，乙能解决的概率是13，两人试图独立地在半小时内解决它，则两人都未解决的概率为________，问题得到解决的概率为________．6．从编号为1,2，…，10的10个大小相同的球中任取4个，已知选出4号球的条件下，选出球的最大号码为6的概率为________．7．1号箱中有2个白球和4个红球，2号箱中有5个白球和3个红球，现随机地从1。