半径、缓和曲线设计及主点里程桩号计算

第四章 横断面设计4-1 某新建三级公路，设计速度V ＝30km/h ，路面宽度B ＝7m ，路拱%2=G i ，路肩m b J 75.0=，路肩横坡%3=J i 。

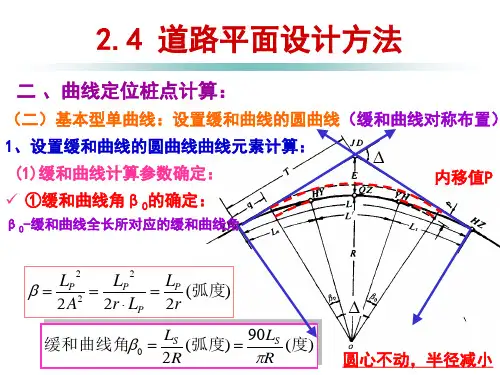
某平曲线转角800534'''= α，半径m R 150=，缓和曲线m L s 40=，加宽值m b 7.0=，超高%3=h i ，交点桩号为K7+086.42。

试求平曲线上5个主点及下列桩号的路基路面宽度、横断面上的高程与设计高程之差：① K7+030；②K7+080；③K7+140；④K7+160。

解：已知：JD ＝K7+086.42，800534'''= α，m R 150=，m L s 40=⑴平曲线要素计算：）（m R L p s44.015024402422=⨯==）（m R L l q S s 99.191502404024024022323=⨯-=-=）（m tg q tg p R T 19.6799.192800534)0.44150(2)(=+'''⋅+=+⋅+== α)(21.13140800534150180L 180m R L s =+'''⨯⨯=+=παπ)(67.75012800534sec )0.44150(2sec )(m R p R E =-'''⋅+=-⋅+= α）（m L T D 17.321.13119.6722=-⨯=-= （2）主点里程桩号计算 JD K7+086.42 -T -67.19 ZH K7+019.23 +Ls +40 HY K7+059.23ZH K7+019.23+L/2 +131.21/2 QZ K7+84.84ZH K7+019.23+L +131.21 HZ K7+150.44-Ls -40YH K7+110.44⑶超高过渡及加宽计算：新建三级公路，设计速度V ＝30km/h ，无中间带，超高过渡采用采用内边线旋转，加宽线性过渡，路基边缘为设计高程，加宽值m b 7.0=，超高%3=h i ，临界断面距过渡段起点m L i i x c h G 67.2640%3%20=⨯=•=。

顶岗实习报告道路工程测量(圆曲线缓和曲线计算公式) 实习时间：2013年7月至2013年9月17日 工程项目名称：乌鲁木齐绕城高速公路（东线）WRDX-3实习报告内容：经过实习的一段时间发现道路测量与建筑测量之间有很大的差别，道路测量主要就是曲线上放样，而建筑测量中为直线直角放样。

因此道路测量人员必须掌握曲线放样的内容。

而曲线放样的内容主要就是圆曲线和缓和曲线，一般采用的方法就是交点放样法和偏角法下面就是我在这一段时间内学习到的关于曲线放样的基本内容。

重点：圆曲线、缓和曲线的要素计算和主点测设方法；切线支距法和偏角法的计算公式和测设方法；路线纵断面的基平、中平测量和横断面测量方法 难点：缓和曲线的要素计算和主点测设方法；缓和曲线的切线支距法和偏角法的计算公式和测设方法。

交点转点转角及里程桩的测设一、 道路工程测量概述分为：路线勘测设计测量 (route reconnaissance and design survey) 和道路施工测量 (road construction survey) 。

（一） 勘测设计测量 (route reconnaissance and design survey) 分为：初测 (preliminary survey) 和定测 (location survey) 1、 初测内容：控制测量 (control survey) 、测带状地形图 (topographical map of a zone)和纵断面图 (profile) 、收集沿线地质水文资料、作纸上定线或现场定线，编制比较方案，为初步设计提供依据。

2、 2、定测内容：在选定设计方案的路线上进行路线中线测量 (center line survey) 、测纵断面图 (profile) 、横断面图 (cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查，为施工图设计提供资料。

《道路勘测设计》课程设计说明书课题名称: 某三级公路路线设计院（系）: 土木建筑分院专业: 交通工程姓名: 饶先鹏班级: 2014级交通工程2班0224号教师签字2016年12月26日目录一、设计说明 (1)1.1课程设计的目的 (1)1.2设计要求 (1)1.3设计原始资料 (1)二、道路定线 (2)2.1道路选线的一般原则 (2)2.2选线的步骤和方法 (2)2.3路线方案比选评价指标 (2)三、平面设计 (4)3.1平面设计的要求和原则 (4)3.2直线设计 (4)3.3曲线设计 (5)3.4有缓和曲线的平曲线要素计算实例 (6)四、纵断面设计 (7)4.1纵断面设计的原则 (7)4.2纵坡及坡长设计 (7)4.3平纵线形组合设计 (8)4.4竖曲线设计 (8)五、横断面设计 (9)5.1道路横断面设计的要求 (10)5.2路肩设计 (10)5.3平曲线加宽超高设计 (10)5.4路基土石方数量计算与调配 (11)六、总结 (12)参考文献 (12)一、设计说明1.1课程设计的目的通过课程设计，让我们的理论知识得到实践，让我们对道路勘察设计有更深刻的了解，以及巩固和扩大所学的专业知识；道路勘测设计是教学计划中重要的实践性教学环节之一，在设计过程中，通过实际工程设计，同时结合课堂学习的知识及课本知识，掌握公路勘测设计的程序和技术方法。

使理论知识与实践相结合，熟悉路线设计的步骤和方法。

进一步巩固和加深及运用课堂上所学的勘测设计原理、标准、方法、理论基础知识，培养我们的分析问题、解决问题、独立设计的能力，使知识更加系统化。

1.2设计要求按地形图上给定的起、讫点及相应设计高程（为起讫点的原地面高程），完成该公路的初步设计的主要设计工作，具体要求如下：1、确定道路等级及主要技术指标。

2、方案图：要求线路的布设能适应地形，土石方工程量少，线形指标满足《规》要求；尽量做到技术上可行，经济上合理。

3、完成路线平面设计图；4、完成路线纵断面设计图；5、完成路基横断面设计图；6、逐桩坐标表；7、完成“直线、曲线及转角表”和“竖曲线表”的填写；8、完成“路基设计表”和“路基土石方计算表”的填写；9、编写设计计算说明书。

第三讲公路平面坐标计算1、平曲线认识道路是一个三维空间的工程结构物，它的中线是一个空间曲线，叫路线，其在水平面的投影就是平面线形。

道路平面线形由于受到沿线地形、地质、水文、气候等自然条件和人为条件的制约而改变方向。

在路线平面方向的转折处为满足行车要求，需要用适当的曲线把前、后直线连接起来，这种曲线称为平曲线。

平曲线包括圆曲线和缓和曲线。

①圆曲线要素主点桩号计算：ZY点里程=JD点里程-TQZ点里程=ZY点里程+L/2 YZ点里程=ZY点里程+LJD里程=QZ里程+D/2（校核）②缓和曲线要素切线长： 外距：曲线长：()s s 18022180l aR l a R L h +=+-=πβπ切线加长：q =/2－3/(240R2)圆曲线相对切线内移量：p = 2/(24R)切曲差 Dh = 2T －Lh上式中：α 为线路转向角；β0为缓和曲线角； 其中q 、p 、β0缓和曲线参数。

ZH 桩号 = JD 桩号－T HY 桩号 = ZH 桩号＋QZ 桩号 = HY 桩号＋L/2YH 桩号 = QZ 桩号＋L/2 = HY 桩号＋L = ZH 桩号＋＋LHZ 桩号 = YH 桩号＋= ZH 桩号＋LhJD 桩号 = ZY 桩号－Th ＋Dh （检核）m)2)(（q tgp R T ++=α）（m 2sec)(R p R E -+=αLs Ls Ls Ls Ls Ls注意：上面计算需要大家掌握主点桩号计算，五大主点：ZH、HY、QZ、YH、HZ，还会遇到一些特殊点例如起点QD、终点ZD、公切点GQ。

可以判断下图即可。

重点知识必须掌握（线元法基础）：直线：曲率为0，起终点半径无穷大。

圆曲线：具有一定曲率半径的圆弧，半径为固定值。

缓和曲线：在直线与圆曲线之间或两个不同半径的圆曲线之间设置的曲率连续变化的曲线（指从直线上半径无穷大到圆曲线的定值之间曲率半径逐渐变化的过渡段），我国公路缓和曲线的形式采用回旋线。

（曲率为半径的倒数）A1,A2——缓和曲线参数R——圆曲线半径Ls1,Ls2——缓和曲线长度一段完整缓和曲线满足公式：A²=R x Ls1，A²=R x Ls2入缓和曲线：从ZH点到HY点，A固定不变，随着Ls1的增大，半径从∞减小到R出缓和曲线：从YH点到HZ点，A固定不变，随着Ls2的减小，半径从R增大到∞如果A²≠R x Ls，那么这段缓和曲线是不完整的，叫做不完整缓和曲线。

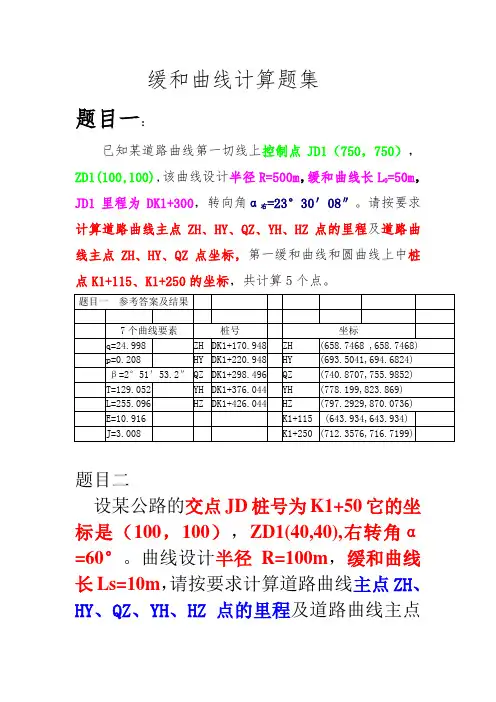
缓和曲线计算题集题目一：已知某道路曲线第一切线上控制点JD1（750，750），ZD1(100,100),该曲线设计半径R=500m，缓和曲线长L0=50m，JD1里程为DK1+300，转向角α右=23°30′08″。

请按要求计算道路曲线主点ZH、HY、QZ、YH、HZ点的里程及道路曲线主点ZH、HY、QZ点坐标，第一缓和曲线和圆曲线上中桩点K1+115、K1+250的坐标，共计算5个点。

题目一参考答案及结果7个曲线要素桩号坐标q=24.998 ZH DK1+170.948 ZH (658.7468 ,658.7468)p=0.208 HY DK1+220.948 HY (693.5041,694.6824)β=2°51′53.2″ QZ DK1+298.496 QZ (740.8707,755.9852)T=129.052 YH DK1+376.044 YH (778.199,823.869)L=255.096 HZ DK1+426.044 HZ (797.2929,870.0736)E=10.916 K1+115 (643.934,643.934)J=3.008 K1+250 (712.3576,716.7199)题目二设某公路的交点JD桩号为K1+50它的坐标是（100，100），ZD1(40,40),右转角α=60°。

曲线设计半径R=100m，缓和曲线长Ls=10m，请按要求计算道路曲线主点ZH、HY、QZ、YH、HZ点的里程及道路曲线主点ZH、HY点坐标及桩点K0+988、K1+000的坐标。

(示意图略)问题：请计算出7个曲线要素，5个主点里程，4个点的坐标。

题目二参考答案及结果7个曲线要素桩号坐标q=4.998 ZH K0+987.241 ZH (坐标X=55.6229 , 坐标Y=55.6229) p=0.042 HY K0+997.241 HY (坐标X=62.5744 , 坐标Y=62.8101) β=2°51′53.2″QZ K1+44.601 QZ (坐标X=85.0106 , 坐标Y=104.0164) T=62.759 YH K1+91.961 YH (坐标X=86.1834 , 坐标Y=150.9202) L=114.72 HZ K1+101.961 HZ (坐标X=83.7569 , 坐标Y=160.6202) E=15.519J=10.798。

45道路工程习题课 第2章道路平面设计一. 含缓和曲线的平曲线几何要素计算公式1.已知平原区某二级公路有一弯道，偏角α右=13°38′42″=13.645°，半径R=800m ，JD=K5+136.53。

假的缓和曲线长度为70，计算曲线主点里程桩号。

或者试计算 ： 1）平曲线要素2）主点ZH ，HY ，QZ ，YH ，HZ 点的桩号解：（1）计算平曲线的几何要素：=（800+0.255）*0.1196+34.998=95.710+34.998=130.708J=2T-L=2×130.708-260.514=0.902（2）主点里程桩号计算：以交点里程桩号为起算点：JD=K5+136.53ZH = JD – T = K5+136.53 -130.708 = K5+5.822HY = ZH + Ls = K5+5.822 +70 = K5+75.822QZ = ZH + L/2= K5+5.822 +260.514/2 =K5+136.079HZ = ZH + L = K5+5.822 +260.514=K5+266.336YH = HZ – Ls = K5+266.336–70=K5+196.336[公式提示] 有缓和曲线的平曲线几何要素计算公式q=L S /2－ L S 3/(240R 2)22700.2552424800Ls p R ===⨯3322707034.99822402240800Ls Ls q R =-=-=⨯13.64580070260.514180180L R Ls ππα=+=⨯⨯+=()sec (8000.255)sec 800 5.85722E R p R αα=+-=+-=()tan 130.7082T R P q α=++=p=L S 2/24R —L S 4/(2688R 3）= L S 2/24R β0=28.6479L S /R T=(R ＋P)tg a/2＋qL=(a －2β0)πR/180＋2L S= 180L R Ls πα=+E=(R ＋P)sec a/2－RJ=2T －L2.圆曲线几何要素计算公式（不含缓和曲线） 曲线主点里程桩号计算计算基点为交点里程桩号，记为JD ，ZY=JD-TYZ=ZY+LQZ=ZY+L/2JD=QZ+D/2 （桩号计算校核）2.某二级公路设计速度为60km/小时，已知JD4交点桩号为K0+750.00, 偏角α右=13°30′,该处的平面线形为单圆曲线，圆曲线半径为600m,试计算该圆曲线的几何元素及曲线主点桩的桩号？解： 圆曲线几何要素计算：已知R=600m, α右=13°30′=13.5°, 则 T=Rtan(a/2)=600×tan(13.5/2)=71.015(m)ππ13.5600L αR=141.372()180180m ⨯⨯==α13.5E R(sec 1)=600(sec 1)=4.188(m)22=-⨯- D=2T-L =2×71.015-141.372=0.658(m)曲线主点桩号计算：ZY=JD-T= K0+750.000-71.015= K0+678.985YZ=ZY+L= K0+678.985 +141.372= K0+820.357QZ=ZY+L/2= K0+678.985+70.866= K0+749.671桩号计算校核 JD 桩号=QZ+D/2= K0+749.671+（0.658/2）= K0+750.00= JD 桩号αT Rtg2πL αR=0.01745αR 180αE R(sec 1)22T L D ===-=-3.与横向力计算公式与因素根据汽车行驶在曲线上力的平衡式计算曲线半径：当设超高时： 式中：V ——计算行车速度，（km/h ）；μ——横向力系数；i h ——超高横坡度；i 1——路面横坡度。

缓和曲线计算(仅供参考)一、概念曲率半径从某一个值连续匀变为另一个值的曲线称为缓和曲线。

二、缓和曲线的已知参数和特征参数1、已知参数(1) 转角α(2) 圆曲线半径R(3) 缓和曲线长度l s2、缓和曲线特征参数与表达式为了便于说明缓圆曲线特征参数，预先建立直角坐标系ZH点是坐标系原点，ZH至JD点为X轴，过ZH点作X轴的垂直方向为Y轴，形成一个直角坐标系，ZH-HY、HY-ZH是缓圆曲线如图所示。

图、对称缓圆曲线(1) 回旋曲线参数：取图一部分放大如图中，曲线段ZH-HY是缓圆曲线。

回旋曲线是我国应用缓圆曲线的常用线型。

根据一般曲线曲率半径的表达特征，回旋曲线曲率半径表达式为ρ＝c／l （3-01）而半径的表达式为 c ＝Rl s （3-02）(2) 切线角：过缓圆曲线上P 点的切线与缓圆曲线ZH 点切线夹角，称为切线角用β表示。

设P 点附近存在dl 对应的d β为dβ＝dl/ρ整理得d β＝dl/Rl s积分上式得切线角表达式β=l 2／2Rl s (3-03)角度表达式 β=l 290°／Rl s (3-04)当l=ls 时，有 βs =l s ／2R (3-05)角度表达式 βs=l s 90°／R(3-06) (3) 缓圆曲线HY 点的点位坐标：图中，把过ZH 点的切线设为X 轴，过ZH 点作X 轴的垂直方向的直线设为Y 轴，形成缓圆曲线直角坐标系。

在P 点处相对于dl 的变化引起P 点的坐标变化，即dx=dl , dy=dl (3-07)积分处理，舍高次项得缓和曲线上任一点点坐标为x=l-l 5/40R 2l 2s +l 9/3456R 4l 4s -l 13/599040R 6l 6s +l 17/175472640R 8l 8s -l 21/78033715200R 10l10s (3-13) y=l 3/6Rl s -l 7/336R 3l 3s +l 11/42240R 5l 5s -l 15/9676800R 7l 7s +l 19/3530096640R 9l 9s -l 23/1880240947200R 11l11s (3-14)舍去第4项以后各项,有 x=l-l 5/40R 2l 2 s +l 9/3456R 4l 4 sy=l 3/6Rl s -l 7/336R 3l 3s +l 11/42240R 5l 5s (3-15)当l=l s 时,缓圆曲线HY 点的坐标为x s =l s -l 3 s /40R 2+l 5 s /3456R 4,y s =l 2 s /6R-l 4 s /336R 3+l 6 s /42240R 5(3-18) (4) 缓圆曲线内移参数p 与切线增值参数q:图中,在路线中线转弯处如果只设计缓圆曲线,路线中线的F,G 点分别是缓圆曲线(虚线)的ZY,YZ 点.在这种情况 下, 车辆沿AF 直线段运行后在F 处处转入圆曲线,这时的线型必须有相应的变化。

曲线坐标计算一、 圆曲线 圆曲线要素：α---------------曲线转向角R---------------曲线半径根据α及R 可以求出以下要素：T----------------切线长L----------------曲线长E----------------外矢距q----------------切曲差两切线长与曲线全长之差 各要素的计算公式为：︒⋅=180παR L 弧长)12(sec -=αR E sec α=cos α的倒数圆曲线主点里程：ZY=JD －TQZ=ZY ＋L ／2 或 QZ=JD －q /2YZ=QZ ＋L ／2 或 YZ=JD ＋T －qJD=QZ ＋q ／2校核用1、基本知识◆ 里程：由线路起点算起,沿线路中线到该中线桩的距离;◆ 表示方法：DK26＋;“+”号前为公里数,即26km,“+”后为米数,即284.56m;CK ——表示初测导线的里程;DK ——表示定测中线的里程;Ｋ——表示竣工后的连续里程;铁路和公路计算方法略有不同;2、曲线点坐标计算偏角法或弦切角法已知条件：起点、终点及各交点的坐标;1计算ZY、YZ点坐标通用公式：2计算曲线点坐标①计算坐标方位角i 点为曲线上任意一点;li 为i 点与ZY点里程之差;弧长所对的圆心角弦切角弦的方位角当曲线左转时用“-”,右转时用“+”;②计算弦长③计算曲线点坐标此时的已知数据为：ZY x ZY,y ZY、 ZY- i、 C;根据坐标正算原理：切线支距法这种方法是以曲线起点ZY或终点YZ为坐标原点,以切线为X 轴,以过原点的半径为Y轴,则圆曲线上任意一点的切线支距坐标可通过以下公式求得：利用坐标平移和旋转,该点在大地平面直角坐标系中的坐标可由以下公式求得：式中：α为ZYYZ点沿线路前进方向的切线方位角;当起点为ZY时,“±”取“＋”,X0=XZY, Y0=YZY, 曲线为左偏时应以yi=-yi代入；当起点为YZ 时,“±”取“-”,X0=XYZ, Y0=YYZ, 曲线为左偏时应以yi=-yi代入；注：1、同弧所对的圆周角等于圆心角的一半2、切线性质圆的切线与过切点的半径相垂直3、弦切角定理弦切角等于它所夹弧上的圆周角4、弧长公式由 L/πR=n°/180°得L=n°πR/ 180°=nπR/180二、缓和曲线回旋线缓和曲线主要有以下几类：A：对称完整缓和曲线基本形------切线长、ls1与ls2都相等;B: 非对称完整缓和曲线---------------切线长、ls1与ls2都不相等C: 非完整缓和曲线卵形曲线----连接两个同向、半径不等的圆的缓和段所组成的卵形曲线D: 回头曲线------------回头曲线是一种半径小、转弯急、线型标准低的曲线形式,其转角接近、等于或大于180度;1、基本形缓和曲线基本公式：ρ=A2/l A=√Rlsρ为缓和曲线上任意点的曲率半径A为回旋线参数l为缓和曲线上任意点到起点ZH的距离弧长ls为缓和曲线的全长切线角公式：缓和曲线直角坐标任意一点P 处取一微分弧段ds ,其所对应的中心角为d β xdx=dscos β xdy=dssin β x缓和曲线常数主曲线的内移值p 及切线增长值q内移值：p=Y s-R1-cosβs=l s2/24R切线增长值：q=X s-Rsinβs=l s/2-ls3/240R2缓和曲线的总偏角及总弦长总偏角：βs=l s/2R 180／Π总弦长：C s=l s-l s3/90R2缓和曲线要素计算切线长外距曲线长圆曲线长切线差平曲线五个基本桩号：ZH ——HY ——QZ ——YH ——HZ缓和曲线主点里程：ZH=JD-T HY=ZH+Ls YH=HY+Ly HZ=YH+LsQZ=ZH+L总/2=HZ-L总/2 JD=QZ+q/2校核缓和曲线上任意点坐标计算切线支距法：以缓和曲线起点ZHHZ点为坐标原点,起点的切线为x轴,过原点的垂直于切线的垂线为y轴建立坐标系,则缓和曲线上任意一点的切线支距坐标可通过以下公式求得：利用坐标平移和旋转,该点在大地平面直角坐标系中的坐标可由以下公式求得：式中：α为ZHHZ点沿线路前进方向的切线方位角;当起点为ZH时,“±”取“＋”,X0=XZH, Y0=YZH, 曲线为左偏时应以yi=-yi代入；当起点为HZ 时,“±”取“-”,X0=XHZ, Y0=YHZ, 曲线为左偏时应以yi=-yi代入；曲线上任意点的方位角αi=αZH或HZ±ββ为切线角±为右转“﹢”左转“﹣”当点位于圆曲线上,有：其中, , 为点到坐标原点的曲线长;2、非对称完整缓和曲线由于受特殊地形和地物条件限制采用对称缓和曲线型平曲线难以与地形条件相结合,于是引入非对称缓和曲线型平曲线;非对称缓和曲线在计算时较困难,不能简单套用对称缓和曲线的公式;以下阐述非对称缓和曲线几何要素和任意点坐标及方位角的计算原理;1计算原理如图1所示,平曲线由非对称缓和曲线Ls1、Ls2及半径R的圆曲线组成,JD 为平曲线切线交点,转角α;由于平曲线两端的缓和曲线不等长,因此在计算平曲线各要素时就不能简单套用等长缓和曲线的计算公式;平曲线各要素计算：注：第一式最后一项应 +q1根据交点坐标和切线长计算缓和曲线起点ZH或HZ坐标：XZH=XJD+T1×COSαYZH=YJD+T1×Sinαα为JD～ZH方位角XHZ=XJD+ T2×COSαYZH=YJD+T2×Sinαα为JD～HZ方位角曲线上任意点坐标按基本型缓和曲线的切线支距法和坐标变换、旋转来计算求出;3、非完整缓和曲线卵形曲线卵形曲线是指在两个同向、半径不等的圆曲线间插入一段不完整的缓和曲线,即卵形曲线是缓和曲线的一段,在插入时去掉了靠近半径无穷大方向的一段;首先需要计算出实际并不存在只是在计算过程中起辅助作用的完整缓和曲线段的起点即ZH或HZ点桩号、坐标和切线方位角;这样卵形曲线段的计算就转化为完整缓和曲线段的计算;（1）卵形曲线参数式中：R大,R小为卵形曲线相连的两圆曲线半径,为非完整缓和曲线段即卵形曲线段长度;（2）与相对应的完整缓和曲线的长度为（3）卵形曲线的起点Q接大半径圆的点至假设存在的完整缓和曲线起点ZH 或HZ点的弧长为或 =－（4）与对应的弦长为又因为βQ-------切线角ΔQ-------切点Q至假设起点ZHHZ的弦切角故可得,Q点至ZH点的方位角ZH点的切线方位角Q点至HZ点的方位角HZ点的切线方位角求得卵形曲线起点Q至ZHHZ的弦长和方位角后,则ZHHZ点的坐标为求出假设的ZHHZ点的坐标后,就可以根据基本形缓和曲线的计算方法来计算曲线上任意点的坐标;上面的公式3到11是以不完整缓和曲线的起点Q 接大圆点来计算假设的完整缓和曲线起点ZHHZ 的坐标;也可以以接小圆的缓和曲线终点YHHY 来计算起点ZHHZ 坐标;如下：① 与相对应的完整缓和曲线的长度为 ② 与对应的的弦长为 总弦长： C s = l s -l s 5/90R 2 l s 2= l s -l s 3/90R 2③ 接小圆的YHHY 点的切线角总偏角： βs =l s /2R 180／Π④ 接小圆的YHHY 点到假设起点ZHHZ 的弦切角⑤ 设接小圆的YHHY 点为Z,则Z 点至ZH 点的方位角αZ-ZH=αZ ＋180±Rl b s3200==δ ⑥ ZH 点的切线方位角αZH=αZ ±βZ⑦ Z 点至HZ 点的方位角αZ-HZ=αZ ±Rl b s3200==δ ⑧ HZ 点的切线方位角αHZ=αZ ±βZ⑨ ZHHZ 点的坐标为 设接小圆的YHHY 点为ZXZH 或HZ=XZ+ C s cos αZ-ZHHZYZH 或HZ=YZ+ C s Sin αZ-ZHHZ C s 为弦长注：卵形曲线上大圆包含小圆,也就是说接小圆处的曲率半径为R 小,沿大圆方向曲率半径渐大;假设的完整缓和曲线的起点ZHHZ在大圆那边;4、回头曲线什么是回头曲线回头曲线是一种半径小、转弯急、线型标准低的曲线形式,其转角接近、等于或大于180度;在实际中,我们确实经常在山区道路碰到回头曲线,基本的感觉就是一个急弯,并且转了一百八十度,跟掉头差不多,也就是前面描述的：转角接近、等于或大于180度;下图是湘西“公路奇观”的连续回头曲线;这里所讨论的回头曲线,主要是基于其平面坐标计算的特殊性而言的,它只有一个定义,就是：转角大于或等于180度,由于实际使用中很少有转角正好等于180度的情况,所以就是指转角大于180度这种情况了;为什么这么定义呢,因为一般情况下,交点与曲线的关系是：交点在曲线的外侧,即便是转角接近180度,它的交点也在曲线外侧,如下图：而当转角等于180度时,则成为两条平行线,没有交点,或者说无限远,其曲线位置不具有唯一性,这种情况实际中几乎不会采用；而当转角大于180度时,则交点的位置就比较特殊了,如下图：这个图中,JD1和JD3是普通情况下的交点,均在曲线的外侧,而JD2的转角大于180度,其位置在曲线的内侧,这种情况,才是本此讨论的回头曲线;回头曲线的计算1曲线要素的计算先看一个案例,邵怀高速公路溆浦连接线二级公路,有一个回头曲线,其曲线设计参数如下：JD5,交点坐标X=,Y=,转角224°08′″左转,半径60m,缓和曲线长35m,曲线ZH 点桩号K49+,切线方位角359°23′″,平面图形如下所示：交点桩号：ZH点桩号K49+加上切线长T,结果为K49+;从这个计算结果来看,我们发现与一般曲线要素不同的地方是：1．切线长T和外距E为负值；2．交点桩号比ZH点桩号小;设计文件中的直曲表数据也表明了这一点：2中桩坐标的计算虽然回头曲线的曲线要素与普通曲线有一些特别的地方,但现在我们更关心的是,按照普通平曲线的中桩坐标计算公式,能否计算出准确的结果;答案肯定是不能的,否则我也不会写这篇文章,在这里白费神了;中间具体的计算过程我就不展示了,按照普通平曲线的中桩坐标计算公式,能够计算出各个桩号的坐标,只可惜是错误的结果;按照这个错误的结果,展示该回头曲线的图形如下：回头曲线的处理回头曲线按照普通曲线中桩坐标计算方法不能得到正确的结果,原因在于它的交点实际在曲线内侧,而程序则把它当作普通曲线来处理,从上面那个图形即可看出;处理的方法很简单,就是把回头曲线一分为二,分成两个普通曲线,如下图所示,将JD5对称地分为JD5a和JD5b;这样,只要把JD5 a和JD5b当作普通曲线交点进行计算就行了;首先需要确定JD5 a和JD5b的相关参数,先看JD5a;1计算终点;显然,JD5a的计算终点就是回头曲线的曲中点,从设计文件直曲表上可查得,是K49+；2本交点桩号;JD5a的桩号嘛,应该是回头曲线的ZH点加上JD5a曲线的第一切线长;回头曲线的ZH点在直曲表上有,K49+,而JD5a曲线的第一切线长,那就需要计算一下了;根据示意图,由于图形的对称性,JD5a和JD5b的切线长有两个：T1和T2, JD5a的曲线要素为：半径R=60m,第一缓和曲线Ls1=35m,第二缓和曲线Ls2=0m,交点转角是回头曲线转角的一半,即224°08′″/2=112°04′″,可计算得：T1=106.865m,T2=89.986m;则JD5a的桩号= +=3本交点X/Y坐标;根据坐标正算原理,按照几何关系,已知JD5的坐标为X=,Y=,JD5-JD5a的距离=+=239.493m,JD5-JD5a的坐标方位角359°23′″,容易得出JD5a的坐标为：X=,Y=;4交点之前直线方位角,就是JD5-JD5a的坐标方位角359°23′″也是JD5ZH 点的方位角;5交点转角;交点转角是回头曲线转角的一半,即224°08′″/2=112°04′″,左转; 6平曲线半径及缓和曲线长度;半径R=60m,第一缓和曲线Ls1=35m,第二缓和曲线Ls2=0m;7交点计算起终点桩号;就是曲线的起终点桩号,~到此,JD5a数据搞定;JD5b的数据,计算方法和前面基本一致,结果如下：计算终点：；交点桩号：；交点坐标：X=,Y=；交点之前直线方位角：247°19′07″；交点转角：112°04′″,左转；半径R=60m, Ls1=0m,第二缓和曲线Ls2=35m；交点计算起终点桩号：~;参数数据计算出来后,就可以按普通平曲线的计算方法来计算出回头曲线上任意点的坐标;案例当中回头曲线逐桩坐标表：。