第一部分 第一章 小专题大智慧 对角线规则
- 格式:ppt
- 大小:1.04 MB
- 文档页数:12


高中数学选修知识点总结(全)高中数学选修知识点总结(全)高中数学选修4-1知识点总结平行线等分线段定理平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等。
推理1:经过三角形一边的中点与另一边平行的直线必平分第三边。
推理2:经过梯形一腰的中点,且与底边平行的直线平分另一腰。
平分线分线段成比例定理平分线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。
相似三角形的判定及性质相似三角形的判定:定义:对应角相等,对应边成比例的两个三角形叫做相似三角形。
相似三角形对应边的比值叫做相似比(或相似系数)。
由于从定义出发判断两个三角形是否相似,需考虑6个元素,即三组对应角是否分别相等,三组对应边是否分别成比例,显然比较麻烦。
所以我们曾经给出过如下几个判定两个三角形相似的简单方法:(1)两角对应相等,两三角形相似;(2)两边对应成比例且夹角相等,两三角形相似;(3)三边对应成比例,两三角形相似。
预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似。
判定定理1:对于任意两个三角形,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
简述为:两角对应相等,两三角形相似。
判定定理2:对于任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似。
简述为:两边对应成比例且夹角相等,两三角形相似。
判定定理3:对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似。
简述为:三边对应成比例,两三角形相似。
引理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
定理:(1)如果两个直角三角形有一个锐角对应相等,那么它们相似;(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似。


“对角线规则”教学内容的挖掘与拓展作者:苑凌云岳文虹杨吉来源:《化学教学》2020年第03期摘要:通过梳理初、高中教材“对角线规则”相关知识,明确各阶段学生需达到的进阶目标和思维层级;简述“对角线规则”在近年高考试题中的应用,说明对角线规则对推理预测陌生元素性质的重要作用。
补充教材中位于对角线上的元素“锂-镁、铍-铝、硼-硅”性质的相似之处,并拓展至“碳-磷、氮-硫、氧-氯”元素,于深度和广度上挖掘和拓展“对角线规则”,帮助学生建立完整的元素周期律体系,培养基于“位-构-性”认知模型分析复杂问题的能力。
关键词:元素周期律; 对角线规则; 位-构-性文章编号: 1005-6629(2020)03-0080-06中图分类号: G633.8文献标识码: B1; 问题的提出1869年,俄国化学家门捷列夫通过对已经发现的63种元素进行详尽地分析和考察,依原子量的相对大小按序排列,并把相似性质的元素放于同一纵行,编制出了第一张较为系统的元素周期表。
恩格斯称这一发现“完成了科学史上的一个勋业,这个勋业恐怕可以和勒维烈计算尚未知道的行星海王星的轨道居于同等地位”[1]。
编制元素周期表时,门捷列夫大胆地为尚未发现的元素留下空位,随着科学技术的进步,这些元素一一被发现,充分证明了元素周期表的推理预测功能。
元素周期表不仅可以反映原子的位置结构,更揭示了众多元素间的内在联系和递变规律,是化学发展史上的重要里程碑,“对角线规则”即为元素周期律的重要应用之一。
“对角线规则”是人教版化学选修3《物质结构与性质》第一章第二节“科学探究”栏目中的一则内容,教材叙述较为简单,很多教师在授课时也只是一语带过,但笔者通过分析近几年高考试题,发现很多考题中都潜藏了对角线规则的拓展应用;另外,脑科学证明:零散、孤立的知识点很难在大脑中留下长久印象,只有掌握了系统的分析方法,才能够对信息进行加工处理,从而内化到自己的认知系统中。
元素周期律旨在帮助学生建立“位置-结构-性质”的系统思维框架,从而培养学生基于元素周期律的推理演绎能力;“对角线规则”则丰富了学生的认知系统,提供了更多的逻辑判据,對更全面地诠释元素周期律、发挥元素周期表的功能大有裨益。

初中几何辅助线口诀三角形图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接那么成中位线。
三角形中有中线,延长中线等中线。
四边形平行四边形出现,对称中心等分点。
梯形里面作高线,平移一腰试试看。
平行移动对角线,补成三角形常见。
证相似,比线段,添线平行成习惯。
等积式子比例换,寻找线段很关键。
直接证明有困难,等量代换少麻烦。
斜边上面作高线,比例中项一大片。
圆半径与弦长计算,弦心距来中间站。
圆上假设有一切线,切点圆心半径连。
切线长度的计算,勾股定理最方便。
要想证明是切线,半径垂线仔细辨。
是直径,成半圆,想成直角径连弦。
弧有中点圆心连,垂径定理要记全。
圆周角边两条弦,直径和弦端点连。
弦切角边切线弦,同弧对角等找完。
要想作个外接圆,各边作出中垂线。
还要作个内接圆,内角平分线梦圆如果遇到相交圆,不要忘作公共弦。
内外相切的两圆,经过切点公切线。
假设是添上连心线,切点肯定在上面。
要作等角添个圆,证明题目少困难。
辅助线,是虚线,画图注意勿改变。
假设图形较分散,对称旋转去实验。
根本作图很关键,平时掌握要熟练。
解题还要多心眼,经常总结方法显。
切勿盲目乱添线,方法灵活应多变。
分析综合方法选,困难再多也会减。
虚心勤学加苦练,成绩上升成直线作辅助线的方法一、中点、中位线,延线,平行线。
如遇条件中有中点,中线、中位线等,那么过中点,延长中线或中位线作辅助线,使延长的某一段等于中线或中位线;另一种辅助线是过中点作边或线段的平行线,以到达应用某个定理或造成全等的目的。
二、垂线、分角线,翻转全等连。
如遇条件中,有垂线或角的平分线,可以把图形按轴对称的方法,并借助其他条件,而旋转180度,得到全等形,,这时辅助线的做法就会应运而生。
其对称轴往往是垂线或角的平分线。
三、边边假设相等,旋转做实验。

2 6.3(1)11 x 2y 0 12 2x 4y 3 0 (2)1i 2x y 0123x y 70.1(1)⑵2C ifi (x y) 0 ⑴P o (X O y o )C i C 2⑵[归纳・升华・领悟]ax 2 bx c 0a 0 >0 2a 0 0 1a 0<0 0a 01a 0>0 2抬象问題情境化,新知无弗自通[ P43]C 2f2(x y) 0.? fi(x o yo ) 0fg(xg yo )_0. ji(x y ) 0f 2X y _0a丰0, △= 01相切a z 0,&00相离直线与a= 01直线与抛物线的对称轴平行,两者相交抛物线a z 0,A>02相交a z 0,△= 01相切a z 0,&00相离E■量 U |直线与圆锥曲线的位置关系[例1]已知直线I: kx-y + 2= 0,双曲线C: x2—4y2= 4,当k为何值时:(1) 1与C无公共点;(2) 1与C有惟一公共点;(3) 1与C有两个不同的公共点.[思路点拨]直线与圆锥曲线公共点的个数就是直线与圆锥曲线方程所组成的方程组解的个数,从而问题可转化为由方程组的解的个数来确定参数k的取值.[精解详析]将直线与双曲线方程联立消去y,得(1 —4k2)x2—16kx—20= 0•①当1 —4k2工0时,有△= (—16k)2—4(1 —4k2) (—20) = 16(5 —4k2).(1) 当1 —4k2工0且△< 0,即卩k v —宁或心于时,I与C无公共点.(2) 当1 —4k2= 0,即k=号时,显然方程①只有一解.当1 —4k2工0, △= 0,即k = 时,方程①只有一解.故当k= ±1或k= 时,I与C有惟一公共点.(3) 当1 —4k2M 0,且△> 0时,即一_25v k v宁,且k z g时,方程有两解,I与C有两个公共点.鬲频考点题组化.名师一点就通[对应学生用书P44][一点通]直线与圆锥曲线的位置关系,可以通过讨论直线方程与曲线方程组成的方程组的实数解的个数来确定,通常消去方程组中变量y(或x)得到关于变量x(或y)的一元二次方程,考虑该一元二次方程的判别式△,则有:40?直线与圆锥曲线相交于两个点;△= 0?直线与圆锥曲线相交于一个点;&0?直线与圆锥曲线无交点.x221•对不同的实数值m,讨论直线y= x + m与椭圆4 + 卜1的位置关系.解:y= x+ m, 由2 2田X 2 .14+y =1,消去y得4 +(x+m)2= 1,整理得5x2+ 8mx+ 4m2—4= 0.△= (8m)2—4 X 5(4m2—4)= 16(5 —m2).当一_5<m< ,5时,少0,直线与椭圆相交;当m=—5或m= 5时,A= 0,直线与椭圆相切;当m< —V5或m> ,5时,&0 ,直线与椭圆相离.2•已知抛物线的方程为y2= 4x,直线I过定点P(—2,1),斜率为k, k为何值时,直线I与抛物线y2= 4x只有一个公共点;有两个公共点;没有公共点?解:(1)当k= 0时,直线I与x轴平行,易知与抛物线只有一个交点.y= k(x + 2 什1, ⑵当k z 0时,联立2 ,l y = 4x,消去x,得ky2—4y + 4(2k+ 1) = 0,△= 16 —4k X 4(2k+ 1).①当△= 0,即k =—1或2时,直线I与抛物线相切,只有一个公共点;②当A>0,即一1<k<2且k z 0时,直线I与抛物线相交,有两个公共点;<0 k<1 k>l 2kl 11 -1 1<k< 丄2 kk< 1lAB 亦 1 X 2 2 (y !y^2 7(X 1 X 2$(1 kAT ) Vo k Ab [(X 1 x 2 ( 4X1X 2]/22谪 2 4 0]普[2]2x y1 5 4F 1AB[]A B2 2[]1x - y- 1 5 4F1(1,0)ly 2(x1)2x y 2 0.”2x y 2 0* 2 2x_ y 15 4A(02)BP 4) 迟3丿2.AB ,^y (X A ~X B $ (y A ~y B J5 2 c 4 2125 5.53)( 2 4)Vr 3A(X 1 y 1) B(X 2 y 2)A By3x 2 5x 0.5X 1 X 23x1X 20.2x y 22 2 X-工1 15 42 22x — y — 2 = 0, 法三:设 Ag y i ), Bg y 2),联立 j x 1 2 3 4 y 2*+.= 1, 、5 4消去 y ,得 3X 2— 5x = 0,则X i , X 2是方程3x 2— 5x = 0的两根. 二 X i + X 2= |.由圆锥曲线的统一定义,得AF i = 15 X (5 -x i ),1F 1B = — X (5 — X 2),[一点通] 弦长的求法:(1) 求出端点坐标,禾U 用两点间的距离公式求解. (2) 结合根与系数的关系,利用变形公式 1=7 (1 + k 2 [(X 1 + X 2 2 — 4X 1X 2]或24 20…X i + X 2= ~ , X i X 2= ~,|AB| =Q 1 + 22|x i — X 2|= V 5 • (x i + X 2 — 4x i x 21= , i + k 2[y i + y 22—4y i y 2]求解. (3) 利用圆锥曲线的统一定义求解.3 过抛物线y 2= 8x 的焦点作倾斜角为 45°的直线,则被抛物线截得的弦长为 _____________ 解析:由抛物线y 2 = 8x 的焦点为(2,0), 得直线的方程为 y = x — 2,代入 /= 8x 得(x — 2)2= 8x ,即卩x 2— 12x + 4= 0. X i + X 2 = 12,弦长=X i + X 2 + p = 12 + 4= 16. 答案:16x 224 直线y = 2x — 3与双曲线——y = 1相交于两点A 、B ,贝V AB = _________________ .2解析:设直线y = 2x — 3与双曲线X2 — y 2= 1两交点坐标分别为 A(x i , y i ), B(x 2, y 2).贝U AB = AF i + F i B =X [10 — (X i + X 2)]==.5-=节.得 7x 2— 24x + 20= 0,2 2X6+ 9 = 1的左、右焦点分别为 F i , F 2, 一条直线 A , B 两点,若直线I 的倾斜角为45°求厶ABF 2 2 2 解:由椭圆的方程1-+ y9 = 1知,a = 4, b = 3,I O vJ c =寸 a 2— b 2=-』7.由 c = 7知 F i (— 7, 0), F 2( .7, 0), 又直线I 的斜率k = tan 45 = 1, ■直线I 的方程为x — y + 7= 0.x —y + W = o ,设 A(x 1, y 1), B (X 2, 丫2),则由 £消去 x ,整理得 25y 2— 18 7 y — 81 = 0,+ = 116 9■- |y 1 — y 2|= 寸y + y 2$ — 4y 1y 2= ■ S A ABF 2 = 2|F 1F 2| |y 1 — y 2|=舟 X 2 , 7 X 'g 2 =笃:4"I1两曲线相交的综合问题2 2[例3]已知椭圆补+ y = 1,过点p (2,1)作一弦,使弦在这点被平分,求此弦所在直线16 4 方程.[思路点拨]设出直线的斜率,联立直线与椭圆方程,消去 y ,得关于x 的方程,用根 与系数的关系和弦中点坐标,得斜率的方程,求解即可,也可用“点差法”求解.[精解详析]法一:设所求直线的方程为 y — 1 = k (x — 2),代入椭圆方程并整理,得 (4 k 2 + 1)x 2— 8(2k 2— k)x + 4(2k — 1)2— 16= 0. 又设直线与椭圆的交点为 A(X 1, y 1)、B(x 2, y 2), 则X 1, X 2是上面的方程的两个根,2所以 X 1 + X 2= 84k k + :,4k + 1 因为P 为弦AB 的中点,答案:4755•如图,椭圆 经过F i 与椭圆交于 面积.y 1 + y 2=188125 ,y1y2=—25.4 24 (1)X 1X 2 y 2 2px(p 0)FA(X 1B(X 2 y 2)(2)FA1 FB(1) y 22pxAB x ABpy k(x 处 0) ” k (x p ) ly 2 2px k 2x 2 P(k 22)xk 2^0.X 1X 2AB x X 1 x 2X1X 2FA X 1FB X 2 卫 2.2 .X 1 X 24 (2k k 2 4k 2 1 J 1k -x 2y 4 0.2A(x i y i ) B (X 2 y 2)P AB x 1 x 2 4 y 1 y 2 2A Bx 2 4y 2 16 x 2 4y ; 16(x 2 x 2) 4(y 2 y 2)0 (X 1 X 2)(x 1 X 2) 4(y 1 y 2)(y 1 y 2) 0y 1 y 2 (X 1 x 2) 1 X 1 X 2 4 y 1 y 2 2x 2y 40.[ ]FP1 1 1 1 +一= + - FA FB丄p 丄p X 1+ 2 X 2 + 2X i + X 2 + p 2p X 1 + X 2 + X 1X 2+ 4 X i + X 2 + p2px1+x2+ 2x i + X 2+ p p X i + x 2 + p2— y 2= 1(a > 0)与直线I : x + y = 1相交于两个不同点 A , B.(1)求双曲线C 的离心率e 的取值范围;⑵设直线I 与y 轴的交点为P ,若PA = 12 PB ,求a 的值.2X 2 — y 2 = 1(a > 0)中得(1 — a 2), x 2 + 2a 2x — 2a 2= 0. a1 — a 2z 0, 所以’ 4 o 224a + 8a (1 — a > 0, 解得 0v a v •.2,且 a z 1. 又双曲线的离心率 e =1+ aa 所以e >¥且e z 2.⑵设 A (X 1, y”, B(x 2, y 2), P(0,1),因为 PA = 5P B ,5所以(X 1, y 1— 1) = 12(x 2, y 2 — 1) • 由此得x 1 =亂2由于 X 1, X 2 是方程(1 — a 2)x ?+ 2a ?x — 2a ?= 0 的两根,且 1 — 0,所以不X 2 = — 2,12 1 — a5 2_ 2a 212X2=—1 — a 2.2a 2 289 .17消去x 2,得—匚了= 289•由a >0,解得a =不& (陕西高考)已知动圆过定点 A(4,0),且在y 轴上截得弦 MN 的长为8. (1)求动圆圆心的轨迹 C 的方程;⑵已知点B( — 1,0),设不垂直于x 轴的直线I 与轨迹C 交于不同的两点 P ,Q ,若x 轴7•设双曲线C : 解:(1)将y = — x + 1代入双曲线PBQ l(1)O1(x y)O1A O1M.01y O1O1H MN MN H H MNO1M01A4)y27 (x 4)2 y2旷422y8x(x0)O1 y010O1(0,0)y2 8xC y2 8x.⑵l y kx b(k0)P a P(x1 yj Q(X2y2)/y kx b y2 8x 2 2k2x2 (2bk28) x b2032kb64>0.X1 X28 2bk2k2 b X1X2X y1y2PBQ X1 1X2 1y i(x2 1) y2(x i 1) 0(kx i b)(X2 1) (kx2 b)(X! 1) 02kx i X2 (b k)(X1 X2) 2b 02 22kb2 (k b)(8 2bk) 2k2b 0 k b >0l y k(x 1)l (1,0)[方法-规律•小结]-课下训练经典化"贵在鮭类旁通[ ()]1.曲线X2—xy—y2—3x+ 4y—4= 0与x轴的交点坐标是解当y= 0 时,得X2—3x—4= 0,析:解得X i= 4 或X2=— 1.所以交点坐标为(4,0)和(一1,0).答案:(4,0), (—1,0)22. 曲线X2+ y2= 4与曲线X2+七=1的交点个数为解析:由数形结合可知两曲线有4个交点.答案:43. _________________________ 设抛物线y2= 8X的准线与X轴交于点Q,若过点Q的直线I 与抛物线有公共点,则直线I的斜率的取值范围是.解析:由y2= 8x,得准线方程为x=— 2. 则Q点坐标为(一2,0).设直线y= k(x+ 2).由 /= k(X+ 2) 得k2x2+ (4k2—8)x+ 4k2= 0.y = 8x,若直线I与y2= 8x有公共点,则△=(4k2—8)2—16k4> 0.解得—1 w k w 1.答案:[—1,1]m的范围是4. 曲线y= x2—x+ 2和y= x+ m有两个不同的公共点,则实数解析:消去y,得x2—2x+ 2—m = 0.若有两个不同的公共点,则△= 4 —4(2 —m)>0,/• m>1.答案:(1 ,+^ )2 25•如果椭圆乞+ y = 1的一条弦被点(4,2)平分,那么这条弦所在直线的方程是36 9解析:设直线与椭圆的交点为A(X1, y) B(x2,讨2).T P(4,2)为AB 中点,二X1 + X2= 8, y1 + y2= 4.又••• A, B 在椭圆上,••• x?+ 4y?= 36, x2+ 4y2= 36. 两式相减得(X —x2) + 4(y2—y2)= 0,高中数学即(X i + X 2)(x i — X 2)+ 4(y i + y 2)(y i — y 2)= 0, .y i — y 2 — (X i + X 2= 1X i — X 2 4y + y 2 J 2.1 即直线i 的斜率为一才• ••所求直线方程为 x + 2y — 8= 0. 答案:x + 2y — 8 = 06.已知椭圆的中心在原点,焦点在 X 轴上,长轴长为4.2,离心率为q 6.(1)求椭圆的标准方程;⑵直线l 与该椭圆交于 M 、N 两点,MN 的中点为A(2,— 1),求直线I 的方程.解:(1)由题意2a = 4 2, • a = 2 2,又 e = £ •- c = v :3.•- b 2= a 2 — c 2 = 8— 3= 5.2 2故所求椭圆的标准方程为令+y =1.8 5 (2) •••点A 在椭圆内部,•••过A 点的直线必与椭圆有两交点.当直线斜率不存在时, A 点不可能为弦的中点,故可设直线方程为 y + 1 = k(X — 2),它与椭圆的交点分别为 M(X 1, y 1), N(X 2, y 2),y +1 = kX —2 , 则J X 2 y 2消去y 得匸+七=1.(8k 2+ 5)x 2— 16k(2k + 1)x + 8[(2k + 1)2— 5]= 0,又••• A(2,— 1)为弦MN 的中点, ...x 1 + x 2= 4,5• k = 4,从而直线方程为 5x — 4y — 14= 0.7•已知椭圆C 1与抛物线C 2的焦点均在x 轴上,C 1的中心和C 2的顶点均为原点 0,从 每条曲线上取两个点,将其坐标记录于下表中:• I X 1 + X 2 = 16k 2k + 1^2 '8k 2+ 5 '2x_ 4y2心42(1) C 1 C 2(2)O M O NllC 2FC 1(1)C 2 y 2 2px(p 0)2 yX2p(x 0)4(4 4)C 2 y 2 4x./.、 佗 1b 2 1.F(1,0)k(x 1)C 1M(x 1y 1) N(X 2 y 2)(1x 2y 2 k x2 24k )x X 1 X 28k 2x 4(k 2 1) 8k 2厂47 x1x2o 4y 『2 k(X 1 1) k(X 2 1) k 2[X 1X 2 4 k 21k 2OM(X 1 X 2) 1]8kL 1、4k 2OM ON4k 2 1ON23k21 4k 'X 1X2y 1y 2 0.1.(1)l y kx13k 2 4k 2 1 4k 472 0 y 2x(Ak 2. y 2x 2.AB2 2C i b 1(a>b>0)(2,0)幅豹 < 2 1l 孑 2b 1C 11.高中数学径的圆过椭圆C 的右顶点•求证:直线I 过定点,并求出该定点的坐标.2 2解:⑴由题意设椭圆C 的标准方程为X 2+ y 2= 1(a>b>0) •a b 由题意得a + c = 3, a — c = 1, a = 2, c = 1, b 2 = 3.2 2•••椭圆的标准方程为X +y = i.4 3y = kx + m , I o o ⑵证明:设 A (X 1, y i ), B(X 2, y 2),由S x 2 y 2—+ 匚=1 討 3 (3 + 4k 2) x 2 + 8mkx + 4(m 2— 3) = 0,△= 64m 2k 2 — 16(3 + 4k 2)(m 2— 3)>0 , 即 3 + 4k ? — m 2>0.y 1y 2= (kx 1 + m) (kx 2 + m)2 2=k X 1X 2 + mk(X 1 + X 2) + m =•••以AB 为直径的圆过椭圆的右顶点 D(2,0), k AD k BD =— 1 ,y 1y 2 + X 1X 2 — 2(X 1 + X 2) + 4= 0, 即3亦—4f +皿书+哼+ 4= 0 3+ 4k 3+ 4k 3 + 4k化简得 7m 2+ 16mk + 4k 2 = 0,解得 m 1=— 2k , m 2=—牙,且满足 3 + 4k 2— m 2>0.当m =— 2k 时,I : y = k(x — 2),直线过定点(2,0),与已知矛盾; 当m =—学时,I : y = k x —舟,直线过定点 7, ° • 综上可知,直线I 过定点,定点坐标为7, 0 •得, --X1 + X2 = 一3 m 2 — 4k 2 * 2 *3 + 4k -y 1 . y 2X 1 — 2 X 2— 2 化简得8mk3+ 4k 2'。

大智慧公式教程一、线形函数线形函数要和其它指标函数一起用才能发挥效力,因为它们都是描述其它指标函数的。
正确用好线形函数可以使主副图指标显示丰富多彩,色彩缤纷。
1、函数:STICK 说明:画棒状线,STICK的英文是棍、棒的意思。
如副图公式:C〉REF(C,1) AND C〉REF(C,2),STICK;2、函数:COLORSTICK 说明:以零轴为中心画彩色棒状线,零轴下为阴线颜色,零轴上为阳线颜色,这样零轴就如楚汉交界,泾渭分明了。
如副图公式:C-REF(C,1),COLORSTICK;3、函数:LINESTICK 说明:同时画棒状线与指标线。
LINE是线,STICK是棒,LINESTICK自然是线棒一起显示了。
如副图公式: A:=C-REF(C,1);A,LINESTICK;即想显示指标线和棒状线,又想以零轴为中心上下显示两种彩色棒状线,可以用分开的两句语句来达到目的,如副图公式:A:=C-REF(C,1);A,LINESTICK;A,COLORSTICK;4、函数:VOLSTICK 说明:画成交量柱状线。
这是专门为显示成交量设计的。
如副图公式:VOL,VOLSTICK;5、函数:CROSSDOT 说明:画叉状线或x状线。
CROSS是交叉,DOT是点。
如副图公式:ma1:ma(c,30),CROSSDOT;6、函数:CIRCLEDOT 说明:画小圆圈线,如副图公式:ma1:ma(c,30),CIRCLEDOT;7、函数:LINETHICK 说明:改变指标线粗细。
取1、2、3、4、5、6、7放在LINETHICK后面如:LINETHICK2,数字越大,线越粗,最大可取7。
如副图公式:例1:ma1:ma(close,30),COLORFF00FF,linethick2;例2:A:=C-REF(C,1);A,COLORSTICK,LINETHICK4;8、函数:POINTDOT 说明:画点状线,POINT是点、加点的意思。

(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1) 确定最大边(不妨设为 c );(2) 若c 2= a 2+ b 2,则厶ABC 是以/ C 为直角的三角形;a 2 +b 2vc 2,则此三角形为钝角三角形(其中a 2 +b 2>c 2,则此三角形为锐角三角形(其中 直角三角形斜边上的中线等于斜边的一半 在直角三角形中,如4.注意:(1) (2) (3) c 为最大边); c 为最大边) 那么它所对的直角边等于斜边的一半。
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
学海教育一对一个性化辅导讲义勾股定理及其逆定理1、掌握勾股定理与逆定理3、会用勾股定理及逆定理解决实际问题教学内容【基础知识梳理】」、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为 a ,b ,斜边长为c ,那么勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边2、勾股定理的逆定理: 如果三角形的三边长 a , b , c 有下面关系:a 2+ b 2= c 2,那么这个三角形是直角三角形。
勾股数:满足a 2+ b 2= c 2的三个正整数叫做勾股数(注意:若a , b , c 、为勾股数,那么 k a , kb , kc 同样也是勾股数组。
)* 附:常见勾股数:3,4,5 ; 6,8,10 ; 9,12,15 ; 5,12,132 2 23、判断直角三角形:如果三角形的三边长 a 、b 、c 满足a +b =c ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
学员姓名 年级及科目 八年级数学学校 教师 Wang Ion gbiao授课时间:教学目标 2、会用逆定理判断三角形的形状5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。


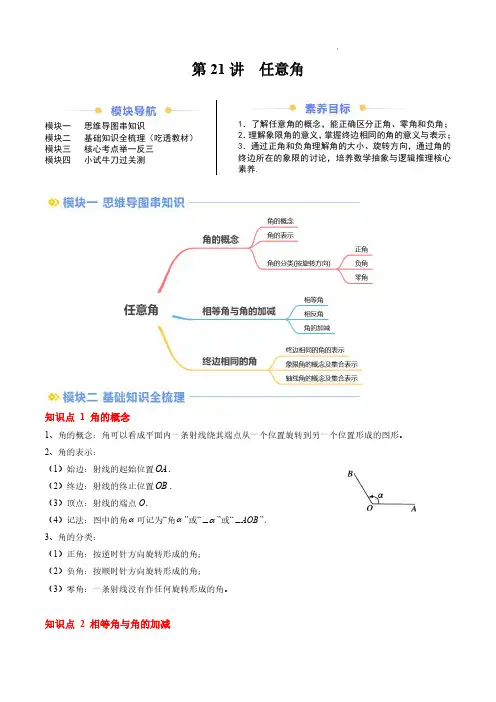
第21讲任意角模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.了解任意角的概念,能正确区分正角、零角和负角;2.理解象限角的意义,掌握终边相同的角的意义与表示;3.通过正角和负角理解角的大小、旋转方向,通过角的终边所在的象限的讨论,培养数学抽象与逻辑推理核心素养.知识点1角的概念1、角的概念:角可以看成平面内一条射线绕其端点从一个位置旋转到另一个位置形成的图形。
2、角的表示:(1)始边:射线的起始位置OA .(2)终边:射线的终止位置OB .(3)顶点:射线的端点O .(4)记法:图中的角α可记为“角α”或“α∠”或“AOB ∠”.3、角的分类:(1)正角:按逆时针方向旋转形成的角;(2)负角:按顺时针方向旋转形成的角;(3)零角:一条射线没有作任何旋转形成的角。
知识点2相等角与角的加减1、相等角:设角α由射线OA 绕端点O 旋转而成,角β由射线O'A'绕端点O'旋转而成,如果他们的旋转方向相同且旋转量相等,那么就称αβ=.2、相反角:把射线OA 绕端点O 按不同方向旋转相同的量所成的两个角叫做互为相反角,角α的相反角记为α-.3、角的加减:记α,β是任意两个角,我们规定:把角α的终边按逆时针旋转角β,这时终边所对应的角是αβ+;按顺时针旋转角β,这时终边所对应的角是αβ-知识点3终边相同的角1、终边相同的角的表示:所有与角α终边相同的角,连同角α在内,可构成一个集合S ,它们彼此相差360()k k Z ⋅∈ ,即{}360,S k k Z ββα==+⋅∈ .【要点辨析】相等的角终边一定相同,但终边相同的角却不一定相等,终边相同的角有无数个,它们之间相差360°的整数倍,要注意角的集合的表示形式不是唯一的。
1、象限角:当角的顶点与坐标原点重合,角的始边与x 轴的非负半轴重合,那么角的终边(除端点外)在第几象限,就说这个角是第几象限;3、轴线角:称这个角为轴线角,这时,这个角不属于任何象限。
102条做初中几何辅导线的规律几何中,同学们最头疼的就是做辅助线了,今天收集了做辅助线的102条规律,从此,孩子们再也不怕了不会做了!家长们赶快为孩子收藏吧!线、角、相交线、平行线规律1如果平面上有n(n≥2)个点,其中任何三点都不在同一直线上,那么每两点画一条直线,一共可以画出n(n-1)条。
规律2平面上的n条直线最多可把平面分成〔n(n+1)+1〕个部分。
规律3如果一条直线上有n个点,那么在这个图形中共有线段的条数为n(n -1)条。
规律4线段(或延长线)上任一点分线段为两段,这两条线段的中点的距离等于线段长的一半。
规律5有公共端点的n条射线所构成的交点的个数一共有n(n-1)个。
规律6如果平面内有n条直线都经过同一点,则可构成小于平角的角共有2n(n-1)个。
规律7如果平面内有n条直线都经过同一点,则可构成n(n-1)对对顶角。
规律8平面上若有n(n≥3)个点,任意三个点不在同一直线上,过任意三点作三角形一共可作出n(n-1)(n-2)个。
规律9互为邻补角的两个角平分线所成的角的度数为90°。
规律10平面上有n条直线相交,最多交点的个数为n(n-1)个。
规律11互为补角中较小角的余角等于这两个互为补角的角的差的一半。
观察内容的选择,我本着先静后动,由近及远的原则,有目的、有计划的先安排与幼儿生活接近的,能理解的观察内容。
随机观察也是不可少的,是相当有趣的,如蜻蜓、蚯蚓、毛毛虫等,孩子一边观察,一边提问,兴趣很浓。
我提供的观察对象,注意形象逼真,色彩鲜明,大小适中,引导幼儿多角度多层面地进行观察,保证每个幼儿看得到,看得清。
看得清才能说得正确。
在观察过程中指导。
我注意帮助幼儿学习正确的观察方法,即按顺序观察和抓住事物的不同特征重点观察,观察与说话相结合,在观察中积累词汇,理解词汇,如一次我抓住时机,引导幼儿观察雷雨,雷雨前天空急剧变化,乌云密布,我问幼儿乌云是什么样子的,有的孩子说:乌云像大海的波浪。
初中几何辅助线的规律初中几何辅助线的规律(一)线、角、相交线、平行线规律1假如平面上有n(n&ge;2)个点,其中任何三点都不在同一直线上,那么每两点画一条直线,一共能够画出n(n-1)条。
规律2平面上的n条直线最多可把平面分成〔n(n+1)+1〕个部分。
规律3假如一条直线上有n个点,那么在这个图形中共有线段的条数为n(n-1)条。
规律4线段(或延长线)上任一点分线段为两段,这两条线段的中点的距离等于线段长的一半。
规律5有公共端点的n条射线所构成的交点的个数一共有n(n—1)个。
规律6假如平面内有n条直线都经过同一点,则可构成小于平角的角共有2n(n-1)个。
规律7假如平面内有n条直线都经过同一点,则可构成n(n-1)对对顶角。
规律8平面上若有n(n≥3)个点,任意三个点不在同一直线上,过任意三点作三角形一共可作出n(n-1)(n-2)个、规律9互为邻补角的两个角平分线所成的角的度数为90&de g;、规律10平面上有n条直线相交,最多交点的个数为n(n—1)个。
规律11互为补角中较小角的余角等于这两个互为补角的角的差的一半。
规律12当两直线平行时,同位角的角平分线互相平行,内错角的角平分线互相平行,同旁内角的角平分线互相垂直。
规律13已知AB∥DE,如图⑴~⑹,规律如下:规律14成“8"字形的两个三角形的一对内角平分线相交所成的角等于另两个内角与的一半。
三角形部分规律15在利用三角形三边关系证明线段不等关系时,假如直截了当证不出来,可连结两点或延长某边构造三角形,使结论中出现的线段在一个或几个三角形中,再利用三边关系定理及不等式性质证题。
注意:利用三角形三边关系定理及推论证题时,常通过引辅助线,把求证的量(或与求证有关的量)移到同一个或几个三角形中去然后再证题。
规律16三角形的一个内角平分线与一个外角平分线相交所成的锐角,等于第三个内角的一半、规律17三角形的两个内角平分线相交所成的钝角等于90o加上第三个内角的一半。