物质结构——晶体分类及空间利用率的计算
- 格式:pdf
- 大小:1.37 MB
- 文档页数:10

晶体密度、空间利用率的通用计算方法以金属晶体为例进行分析,计算方法如下:第一步,确定晶胞含有的微粒数。
若1个晶胞中含有x 个微粒,则: (1)1个晶胞中原子利用的体积 = x ·4 π r 3 / 3 ,其中r 表示金属原子半径。
(2)1个晶胞质量 = x ·M / N A ,其中M 表示金属的摩尔质量,N A 表示阿伏加德罗常数。
若计算对象是离子晶体,该式亦然成立,M 则表示离子化合物的摩尔质量。
第二步,计算晶胞体积。
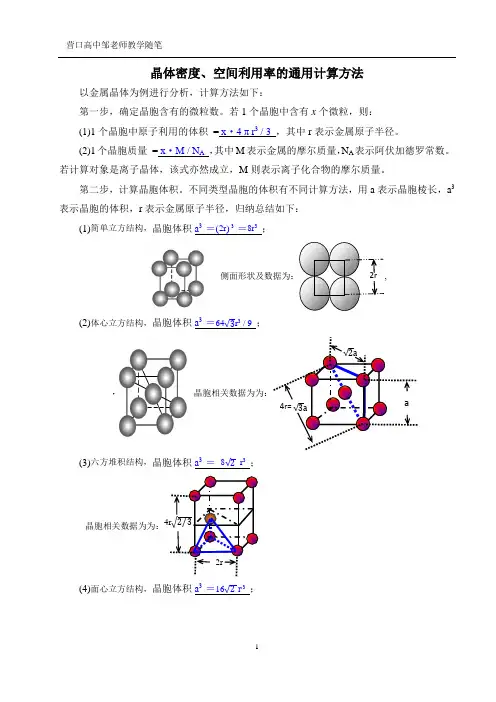
不同类型晶胞的体积有不同计算方法,用a 表示晶胞棱长,a 3表示晶胞的体积,r 表示金属原子半径,归纳总结如下:(1)简单立方结构,晶胞体积a 3 =(2r ) 3 =8r 3 ;侧面形状及数据为:,(2)体心立方结构,晶胞体积a 3 =64√3r 3 / 9 ;(3)六方堆积结构,晶胞体积a 3 = 8√2 r 3 ;晶胞相关数据为为:(4)面心立方结构,晶胞体积a 3 =16√2 r 3 ;a√2a√3a4r= 2r(1)有关晶体密度的计算通用关系式:x·M /N A=ρ·a3,依据是晶体密度等于晶胞密度,具体计算时把各类型晶胞的体积,代入关系式即可,下式亦同。
(2)有关空间利用率的计算通用关系式:x·4 πr3 / 3=w%·a3,其中w% 表示晶胞空间利用率。
注意事项:(1)在实际计算时要注意长度单位换算,晶胞棱长及原子半径单位常用pm,而密度中的体体积单位常用(cm)3,存在换算关系1pm=10-10cm。
(2)若计算离子晶体密度,方法大同小异,需要综合考虑阴、阳离子半径来求晶胞体积。
常见金属晶胞结构与性质归纳一览表:。


晶胞空间利用率公式晶胞空间利用率公式是描述晶体结构中原子或离子排列紧密程度的一个重要参数。
晶体结构是由一定数量的原子或离子按照一定的规律排列而成的,晶胞是晶体中最小的重复单元,晶胞空间利用率是指晶胞中实际占据的原子或离子体积与晶胞总体积之比,是描述晶体结构紧密程度的一个重要参数。
晶胞空间利用率公式为:V = (n × Vm) / Vc其中,V表示晶胞空间利用率,n表示晶胞中实际占据的原子或离子数,Vm表示一个原子或离子的摩尔体积,Vc表示晶胞的体积。
晶胞空间利用率是晶体结构中一个重要的物理量,它反映了晶体中原子或离子排列的紧密程度。
晶体结构中原子或离子的排列方式决定了晶体的物理性质,如硬度、密度、热膨胀系数等。
因此,晶胞空间利用率是研究晶体结构和性质的重要参数。
晶胞空间利用率的大小与晶体结构有关。
对于紧密堆积的晶体结构,晶胞空间利用率较大,如钻石、金刚石等;对于松散堆积的晶体结构,晶胞空间利用率较小,如石墨、石英等。
晶胞空间利用率还与晶体中原子或离子的大小有关,原子或离子越大,晶胞空间利用率越小。
晶胞空间利用率的计算需要知道晶体结构中原子或离子的排列方式和晶胞的大小。
晶体结构可以通过X射线衍射、电子衍射等方法进行测定,晶胞的大小可以通过晶体的晶胞参数计算得到。
因此,晶胞空间利用率的计算需要先确定晶体结构和晶胞参数,然后根据公式进行计算。
晶胞空间利用率的大小对晶体的物理性质有重要影响。
晶胞空间利用率较大的晶体结构通常具有较高的密度和硬度,如钻石、金刚石等;晶胞空间利用率较小的晶体结构通常具有较低的密度和硬度,如石墨、石英等。
晶胞空间利用率还与晶体的热膨胀系数有关,晶胞空间利用率较大的晶体结构通常具有较小的热膨胀系数,如钻石、金刚石等;晶胞空间利用率较小的晶体结构通常具有较大的热膨胀系数,如石墨、石英等。
晶胞空间利用率的大小还与晶体的稳定性有关。
晶胞空间利用率较大的晶体结构通常比较稳定,如钻石、金刚石等;晶胞空间利用率较小的晶体结构通常比较不稳定,如石墨、石英等。


金属晶体四类晶胞空间利用率的计算金属晶体四类晶胞空间利用率的计算高二化学·唐金圣在新课标人教版化学选修3《金属晶体》一节中,给出了金属晶体四种堆积方式的晶胞空间利用率。
空间利用率就是晶胞上占有的金属原子的体积与晶胞体积之比。
下面就金属晶体的四种堆积方式计算晶胞的空间利用率。
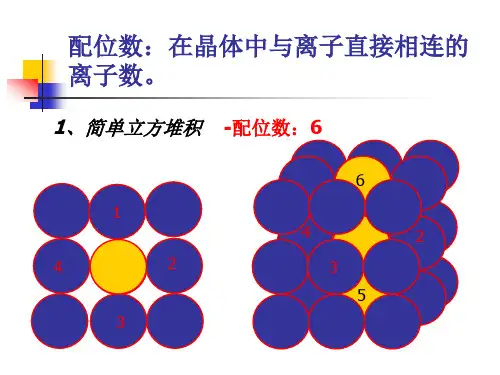
一、简单立方堆积:在简单立方堆积的晶胞中,晶胞边长a等于金属原子半径r的2倍,晶胞的体积V晶胞=(2r)3。
晶胞上占有1个金属原子,金属原子的体积V原子=4πr3/3 ,所以空间利用率V原子/V晶胞 = 4πr3/ (3×(2r)3)=52.33﹪。
二、体心立方堆积:在体心立方堆积的晶胞中,体对角线上的三个原子相切,体对角线长度等于原子半径的4倍。
假定晶胞边长为a ,则a2 + 2a2 = (4r)2, a=4 r/√3 ,晶胞体积V晶胞 =64r3/ 3√3 。
体心堆积的晶胞上占有的原子个数为2,原子占有的体积为V原子=2×(4πr3/3)。
晶胞的空间利用率等于V原子/V晶胞 =(2×4πr3×3√3)/(3×64r3)= 67.98﹪。
三、面心立方最密堆积在面心立方最密堆积的晶胞中,面对角线长度是原子半径的4倍。
假定晶胞边长为a,则a2 + a2 = (4r)2 ,a = 2√2r ,晶胞体积V晶胞=16√2r3。
面心立方堆积的晶胞上占有的原子数为4,原子占有的体积为V原子 = 4×(4πr3/3)。
晶胞的空间利用率等于V原子/V晶胞 =(4×4πr3)/(3×16√2r3)= 74.02﹪.四、六方最密堆积六方最密堆积的晶胞不再是立方结构。
晶胞上、下两个底面为紧密堆积的四个原子中心连成的菱形,边长a = 2r ,夹角分别为60°、120°,底面积s = 2r×2r×sin(60°) 。

晶体空间利用率计算晶体空间利用率(Crystal Packing Efficiency)是指晶体中原子或离子占据晶胞体积的比例,是晶体内部空间的紧密程度的量化指标之一、晶体空间利用率的计算是晶体学中一个重要的概念,可以帮助我们理解晶体结构的紧密程度和稳定性。
在计算晶体空间利用率时,需要考虑晶胞的体积和晶体中原子或离子的体积。
晶体是由晶胞(unit cell)重复堆积而成的,晶胞是晶体的最小重复单元。
晶胞是三维空间中的一个平行六面体,具有一定的形态和尺寸。
晶体中的原子或离子分布在晶胞的特定位置上。
晶胞的体积可以通过晶胞的各个边长(a、b、c)及夹角(α、β、γ)来计算。
晶胞的体积(V)可以用以下公式表示:V = a * b * c * sin(α) * sin(β) * sin(γ)在计算晶体空间利用率时,我们需要考虑晶体中原子或离子的体积。
原子或离子的体积可以通过元素的晶胞中原子或离子数(Z)及原子或离子的半径(r)来计算。
原子或离子的体积(V_atom)可以用以下公式表示:V_atom = (4/3) * π * r^3 * Zη = (V_atom / V) * 100%晶体空间利用率通常介于0到100%之间。
当晶体空间利用率接近100%时,表示晶体中的原子或离子堆积非常紧密,晶体结构稳定性较高。
而当晶体空间利用率较低时,表示晶体中的原子或离子之间存在较多的空隙或间隙,晶体结构相对较松散。
计算晶体空间利用率的一个重要应用是对晶体的密度进行估计。
晶体的密度可以通过晶体的分子量(M)及晶胞的体积(V)来计算。
晶体的密度(ρ)可以用以下公式表示:ρ=(M/V)*10^24通过计算晶体的密度,可以帮助我们研究晶体的物理特性、确定其材料的性质,并且在材料科学和工程领域中具有重要的应用价值。
总结起来,晶体空间利用率是一个衡量晶体内部空间紧密程度的重要指标,可以通过晶胞的体积和晶体中原子或离子的体积来计算。



晶体空间利用率的计算公式晶体空间利用率是指晶体中原子或离子所占据的空间与晶体总空间的比值,是评价晶体紧密程度的重要指标。
晶体空间利用率的计算公式为:V = V_atom / V_cell其中,V表示晶体空间利用率,V_atom表示晶体中原子或离子所占据的空间,V_cell表示晶胞的体积。
晶体空间利用率的计算方法晶体空间利用率的计算方法需要先确定晶体的晶胞类型和晶胞参数,然后计算出晶胞的体积和晶体中原子或离子所占据的空间,最后将两者相除即可得到晶体空间利用率。
以简单立方晶体为例,其晶胞类型为P,晶胞参数为a,晶胞体积为V_cell = a^3。
假设晶体中只有一个原子,其半径为r,则原子所占据的空间为V_atom = (4/3)πr^3。
将V_atom和V_cell代入晶体空间利用率的计算公式中,即可得到简单立方晶体的晶体空间利用率:V = V_atom / V_cell = (4/3)πr^3 / a^3同样的,对于其他晶体类型,也可以根据其晶胞类型和晶胞参数计算出晶胞体积和原子或离子所占据的空间,从而得到晶体空间利用率。
晶体空间利用率的意义晶体空间利用率是评价晶体紧密程度的重要指标,其数值越大,表示晶体中原子或离子所占据的空间越大,晶体越紧密。
晶体空间利用率的大小还与晶体的物理性质密切相关,如密度、硬度、热膨胀系数等,因此晶体空间利用率的计算对于研究晶体的物理性质具有重要意义。
晶体空间利用率还可以用于比较不同晶体之间的紧密程度,从而为晶体的合成和应用提供参考。
例如,在材料科学中,晶体空间利用率可以用于评价材料的结构性能,指导新材料的设计和合成。
晶体空间利用率是评价晶体紧密程度的重要指标,其计算公式简单易懂,可以用于比较不同晶体之间的紧密程度,具有重要的理论和应用价值。