选修三 金属晶体的空间利用率

金属晶体晶胞中原子空间利用率的计算作者：李春文来源：《中学化学》2019年第01期金属晶体中原子堆积方式复杂，每种堆积中原子空间利用率不尽相同，掌握金属晶体里晶胞中原子空间利用率对于解决所有晶胞的原子空间利用率问题具有触类旁通的作用。

研究金属晶体里晶胞中原子空间利用率，首先应该掌握求算它的基本步骤：先找到晶胞中所含原子数，然后根据晶胞中紧邻原子的位置关系找到原子半径与晶胞边长的关系，再根据空间利用率的求算方法即晶胞中原子所占的实际体积与晶胞中原子围成的几何图形的体积之比，求得空间利用率。

一、简单立方堆积简单立方堆积指的是相邻非密置层原子的原子核在同一直线，上的堆积。

这种堆积使晶胞结构为立方体型（如图1所示），处于顶点的两个原子紧邻。

晶胞中所含原子数为8x（1/8）=1，该原子所占的实际体积为（4/3）πr3。

由于处于顶点的两个原子紧邻，则原子半径与晶胞边长的关系为a=2r，那么晶胞中原子所围成的立方体的体积为（2r）3，所以简单立方堆积中原子空间利用率为二、体心立方堆积体心立方堆积指的是非密置层的另一种堆积方式，即将上层金属原子填人下层的金属原子形成的凹穴中，并使非密置层的原子稍稍分离。

每层均照此堆积，这种堆积方式称为体心立方堆积。

这种堆积方式使处于体对角线上的原子緊邻（如图2所示）。

晶胞中所含原子数为8x1/8+1=2，则晶胞中所含原子的实际体积为。

由于处于体对角线的原子紧邻，则原子半径与晶胞边长的关系为，所以体心立方堆积中原子空间利用率为三、六方最密堆积每层都是密置层堆积，堆积方式是将上层原子填入下层原子形成的凹穴中，这样的堆积会得到两种基本堆积方式，按ABABAB……的方式堆积称为六方最密堆积;按ABCABCA……的方式堆积称为面心立方最密堆积。

如图3所示，在六方最密堆积的晶胞结构中，体内原子位于平行六面体的一半的体心，即正三棱柱的体心，该原子与上下6个原子紧邻，则该原子与下面（或上面）3个原子构成正四面体结构。

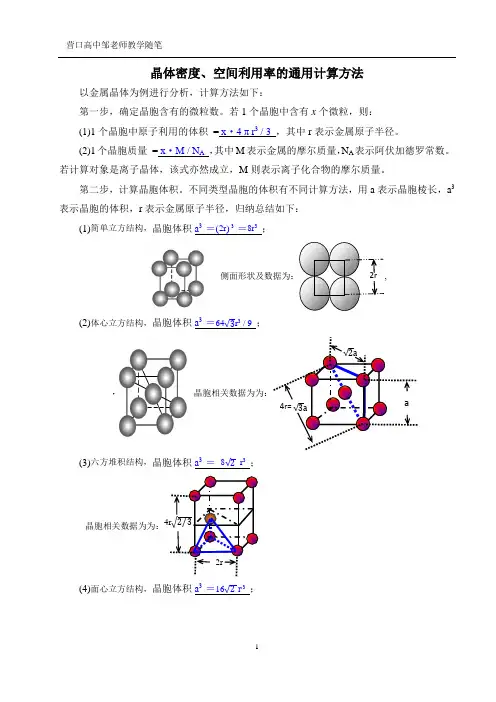
晶体密度、空间利用率的通用计算方法以金属晶体为例进行分析，计算方法如下：第一步，确定晶胞含有的微粒数。

若1个晶胞中含有x 个微粒，则： (1)1个晶胞中原子利用的体积 = x ·4 π r 3 / 3 ，其中r 表示金属原子半径。

(2)1个晶胞质量 = x ·M / N A ，其中M 表示金属的摩尔质量，N A 表示阿伏加德罗常数。

若计算对象是离子晶体，该式亦然成立，M 则表示离子化合物的摩尔质量。

第二步，计算晶胞体积。

不同类型晶胞的体积有不同计算方法，用a 表示晶胞棱长，a 3表示晶胞的体积，r 表示金属原子半径，归纳总结如下：(1)简单立方结构，晶胞体积a 3 ＝(2r ) 3 ＝8r 3 ；侧面形状及数据为：,(2)体心立方结构，晶胞体积a 3 ＝64√3r 3 / 9 ；(3)六方堆积结构，晶胞体积a 3 ＝ 8√2 r 3 ；晶胞相关数据为为：(4)面心立方结构，晶胞体积a 3 ＝16√2 r 3 ；a√2a√3a4r= 2r(1)有关晶体密度的计算通用关系式：x·M /N A＝ρ·a3，依据是晶体密度等于晶胞密度，具体计算时把各类型晶胞的体积，代入关系式即可，下式亦同。

(2)有关空间利用率的计算通用关系式：x·4 πr3 / 3＝w%·a3，其中w% 表示晶胞空间利用率。

注意事项：(1)在实际计算时要注意长度单位换算，晶胞棱长及原子半径单位常用pm，而密度中的体体积单位常用(cm)3，存在换算关系1pm=10-10cm。

(2)若计算离子晶体密度，方法大同小异，需要综合考虑阴、阳离子半径来求晶胞体积。

常见金属晶胞结构与性质归纳一览表：。

金属晶体四类晶胞空间利用率的计算金属晶体四类晶胞空间利用率的计算高二化学·唐金圣在新课标人教版化学选修3《金属晶体》一节中，给出了金属晶体四种堆积方式的晶胞空间利用率。

空间利用率就是晶胞上占有的金属原子的体积与晶胞体积之比。

下面就金属晶体的四种堆积方式计算晶胞的空间利用率。

一、简单立方堆积：在简单立方堆积的晶胞中，晶胞边长a等于金属原子半径r的2倍，晶胞的体积V晶胞=(2r)3。

晶胞上占有1个金属原子，金属原子的体积V原子=4πr3/3 ，所以空间利用率V原子/V晶胞 = 4πr3/ （3×(2r)3）=52.33﹪。

二、体心立方堆积：在体心立方堆积的晶胞中，体对角线上的三个原子相切，体对角线长度等于原子半径的4倍。

假定晶胞边长为a ，则a2 + 2a2 = (4r)2， a=4 r/√3 ，晶胞体积V晶胞 =64r3/ 3√3 。

体心堆积的晶胞上占有的原子个数为2，原子占有的体积为V原子=2×（4πr3/3）。

晶胞的空间利用率等于V原子/V晶胞 =（2×4πr3×3√3）/（3×64r3）= 67.98﹪。

三、面心立方最密堆积在面心立方最密堆积的晶胞中，面对角线长度是原子半径的4倍。

假定晶胞边长为a,则a2 + a2 = (4r)2 ,a = 2√2r ,晶胞体积V晶胞=16√2r3。

面心立方堆积的晶胞上占有的原子数为4，原子占有的体积为V原子 = 4×（4πr3/3）。

晶胞的空间利用率等于V原子/V晶胞 =（4×4πr3）/(3×16√2r3)= 74.02﹪.四、六方最密堆积六方最密堆积的晶胞不再是立方结构。

晶胞上、下两个底面为紧密堆积的四个原子中心连成的菱形，边长a = 2r ,夹角分别为60°、120°，底面积s = 2r×2r×sin(60°) 。

晶体的密堆积摘要：新课程、新教材、新高考，研究新教材，研究新高考，对于广大教师来说时不我待，新教材中存在很多疑难问题，仁者见仁智者见智。

化学选修三《物质结构与性质》第三章，是本模块较难的内容，对学生要求较低，教师授课时要把握好尺度。

关键词：新课程晶体结构密堆积晶胞空间利用率学生在学习化学教材《选修三》第三章时，因为前面教材对这方面的知识涉及很少，对于晶体的堆积方式感到十分困惑，所以笔者针对这个问题进行分析。

由于金属键、离子键、范德华力等没有方向性和饱和性，所以在金属晶体，离子晶体，和一些分子型晶体中，组成晶体的微粒总是趋向于相互配位数高，能充分利用空间的密度大的紧密堆积结构，密堆积方式因充分利用了空间，而使体系的势能尽可能降低，而结构稳定。

为了研究方便，将晶体中的原子，离子等视为具有一定体积的圆球。

空间利用率：单位体积中圆球所占体积的百分数配位数：一个圆球周围的圆球数目一、等径圆球的密堆积把组成金属单质晶体的原子看作是等经圆球。

单层密堆积中只有一种方式，（见人教版教材中图3-22）这种堆积方式中，每个球的配位数为6，在第一层上堆积第二层时，要形成最密堆积，必须把球放在第二层的空隙上。

这样，仅有半数的三角形空隙放进了球，而另一半空隙上方是第二层的空隙。

第一层上放了球的一半三角形空隙，被4个球包围，形成四面体空隙；另一半其上方是第二层球的空隙，被6个球包围，形成八面体空隙。

第二层堆积时形成了两种空隙：四面体空隙和八面体空隙。

那么，在堆积第三层时就会产生两种方式：①六方密堆积（A3密堆积）在等径圆球密置双层之上再放一层，有两种方式，其中之一是和三层中球的位置在密置双层的正四面体空隙之上，即第三层与第一层重复，即采用A BAB…方式堆积（如图a）从中可以抽出六方晶胞，所以称为六方密堆积，（亦叫A3密堆积）配位数为12,空间利用率为74.05％，金属Zn、Mg、Be等属于这种结构。

晶胞为六棱柱的三分之一，平行六面体，截面为平行四边形每个晶胞中含有原子数=1+4x1/12+4x1/6=2A3型堆积方式的空间利用率计算在A3型堆积中取出六方晶胞，平行六面体的底是平行四边形，各边长a=2r，则平行四边形的面积：平行六面体的高②面心立方密堆积（A1型密堆积）放置第三层时，球的位置落在密置双层正八面体空隙之上投影位置即与第二层球错开又与第二层球错开，即采用ABCABC方式堆积（如图b)从中可以抽出立方面心晶胞，所以称为面心立方堆积（也称A1型密堆积）每个晶胞中含4个圆球配位数为12，空间利用率为74.05%。

金属晶体四类晶胞空间利用率的计算高二化学•唐金圣在新课标人教版化学选修 3《金属晶体》一节中，给出了金属晶体四种堆积方式的晶胞空间利用率。

空间利用率就是晶胞上占有的金属原子的体积与晶胞体积之比。

晶体的四种堆积方式计算晶胞的空间利用率。

一、简单立方堆积:在简单立方堆积的晶胞中，晶胞边长 a 等于金属原子半径r 的2倍，晶胞的体积 V 晶胞=(2r)3。

晶胞上占有1个金属原子，金属原子的体积 V 原子=4 n 「3/3 ，所以空间利用率 V 原3 3子/V 晶胞=4 n r / (3X (2r) ) =52.33 % 。

二、体心立方堆积:在体心立方堆积的晶胞中，体对角线上的三个原子相切，体对角线长度等于原子半径的4倍。

假定晶胞边长为a ,则a 2 + 2a 2 = (4r)2, a=4 r/ V 3 ,晶胞体积V 晶胞=64r 3/ 3V 3。

体心堆积的晶胞上占有的原子个数为 2，原子占有的体积为 V 原子=2 X( 4 n r 3/3 )。

晶胞 =(2X 4n r 3x 3V 3) / (3X 64r 3 ) = 67.98% 。

三、面心立方最密堆积在面心立方最密堆积的晶胞中，面对角线长度是原子半径的 则a 2 + a 2 = (4r)2 ,a = 2V 2r ,晶胞体积V 晶胞= 16V 2^。

面心立方堆积的晶胞上占有的原子数为4,原子占有的体积为 V 原子=4 X( 4 n r 3/3 )。

晶胞的空间利用率等于 V 原子N 晶胞= 的空间利用率等于 V 原子N 晶胞 4倍。

假定晶胞边长为a,(4X 4 n r3) /(3 X 16V2r3)= 74.02 % .四、六方最密堆积六方最密堆积的晶胞不再是立方结构。

晶胞上、下两个底面为紧密堆积的四个原子中心连成的菱形，边长a = 2r ,夹角分别为60° 120°，底面积s = 2r x 2r x sin( 60° )。

第三节金属晶体
第二课时
知识目标：
1. 了解金属晶体内原子在平面中的几种常见排列方式。

2．了解金属晶体内原子在立体空间中的常见排列方式。

3．训练学生的动手能力和空间想象能力，培养学生的合作意识。

过程与方法：
1．建立金属原子为等径球体的模型观念。

2．通过亲自排列小球，探究金属原子在平面中的排列方式，以及排列的密集程度。

3．通过粘贴小球，体会原子在三维空间中的堆积过程。

情感态度价值观：
1．通过对金属原子的实际排列过程，锻炼同学的动手能力，在活动过程中，培养学生思考问题，解决问题的能力。

2．养成务实求真、勇于探索的科学态度，重点培养学生“主动参与、乐于探究、交流合作”的精神。

学习重难点：
1．金属晶体的4种基本堆积模型。

2．面心立方最密堆积和六方最密堆积的区别与联系。

3．4种堆积方式所对应的晶胞结果特点。

教学过程
板书设计
第三节金属晶体
一、金属键
二、金属晶体的原子堆积模型
1．简单立方堆积a=2R
空间利用率=52.36%
2．体系立方堆积√3 a = 4R 空间利用率=68.02% 3．体心立方堆积√2 a = 4R 空间利用率=74.05%
4．六方最密堆积a=b=2R 空间利用率=74.05%。