最新多跨静定连续梁受力分析

总第３１８期交　通　科　技ＳｅｒｉａｌＮｏ．３１８　２０２３第３期ＴｒａｎｓｐｏｒｔａｔｉｏｎＳｃｉｅｎｃｅ＆ＴｅｃｈｎｏｌｏｇｙＮｏ．３Ｊｕｎｅ．２０２３ＤＯＩ１０．３９６３／ｊ．ｉｓｓｎ．１６７１ ７５７０．２０２３．０３．０１３收稿日期：２０２３ ０３ ０２第一作者：陈润?（１９９６－），男，硕士生。

连续梁桥临时支墩间距及拆除顺序对其受力状态的影响分析陈润?　石　鑫（武汉理工大学交通与物流工程学院　武汉　４３００６３）摘　要　在连续梁桥施工过程中，合龙后解除临时固结，桥梁由连续刚构体系向多跨连续梁体系的转换是其施工过程最为关键的阶段，故研究连续梁桥施工过程中临时支墩间距及拆除顺序对其受力状态的影响尤为重要。

依托云南水富港大跨连续梁桥，采用ｍｉｄａｓＣｉｖｉｌ有限元模拟软件建立桥梁结构模型，研究其临时支墩间距及拆除顺序对体系转换前后受力状态的影响。

结果表明，大跨连续梁桥施工至边跨合龙段前，不同支墩间距对悬臂状态下的节点累计挠度影响较小；在施工至中跨合龙段后，不同支墩间距对合龙状态下的节点累计挠度影响较大；对于拆除顺序，先拆除中跨侧临时支墩时，Ａ支座与临时支墩支反力均大于先拆除边跨侧临时支墩时，Ｂ支座支反力则相反。

关键词　桥梁工程　连续梁　临时支墩间距　体系转换　拆除顺序中图分类号　Ｕ４４３．３ 大跨预应力连续梁桥采用悬臂施工的方式，先进行悬臂浇筑，待浇筑完毕再进行边跨、中跨合龙及体系转换的施工。

连续梁悬臂浇筑过程中，最为关键的就是合龙后解除临时固结，体系由连续刚构体系向多跨连续梁的转换［１］。

因此，在计算中选择正确的临时固结约束，将理论与实际构造的差异尽量减小，显得十分重要，而且不同的临时固结模拟形式对于主梁受力情况也会产生较大的影响［２］。

左保普［３］以某直线连续梁桥为依托，通过对不同的临时固结参数设置修改，研究主梁内力变化的影响，并提出合理的参数设计范围，从而对临时固结设计进行优化。

余勇继等［４］根据连续梁桥墩梁临时固结体系的受力模式，针对临时支座布置方式提出一种考虑其转动刚度的简化模拟方法，并且推导了转动刚度解析式。

1. 连续梁分析概述比较连续梁和多跨静定梁受均布荷载和温度荷载（上下面的温差）时的反力、位移、内力。

3跨连续两次超静定3跨静定3跨连续1次超静定图 1.1 分析模型2Ø材料钢材: Grade3Ø截面数值 : 箱形截面 400×200×12 mmØ荷载1. 均布荷载 : 1.0 tonf/m2. 温度荷载 : ΔT = 5 ℃ (上下面的温度差)设定基本环境打开新文件，以‘连续梁分析.mgb’为名存档。

单位体系设定为‘m’和‘tonf’。

文件/存档(连续梁分析 )工具 / 单位体系长度> m ; 力 > tonf¿图 1.2 设定单位体系3设定结构类型为 X-Z 平面。

模型 / 结构类型结构类型> X-Z 平面¿设定材料以及截面材料选择钢材GB（S）（中国标准规格），定义截面。

模型 / 材料和截面特性 /45建立节点和单元为了生成连续梁单元，首先输入节点。

捕捉轴线 (关)捕捉单元 (开), 建立节点坐标 ( x, y, z ) ( 0, 0, 0 ) ¿图 1.5 建立节点²参照用户手册的“输入单元时主要考虑事项”用扩展单元功能来建立连续梁。

模型 / 单元/全选扩展类型 > 节点à线单元单元属性> 单元类型 > 梁单元²材料 > 1:Grade3 ; 截面> 1: 400*200*12 ; Beta 角( 0 )生成形式> 复制和移动 ; 复制和移动 > 任意间距方向> x ; 间距( 3@5/3, 8@10/8, 3@5/3 )¿图 1.6 建立单元X Z²输入梁单元. 关于梁单元的详细事项参照在线帮助的“单元类型”的“梁单元”部分6输入边界条件3维空间的节点有6个自由度 (Dx, Dy, Dz, Rx, Ry, Rz)。

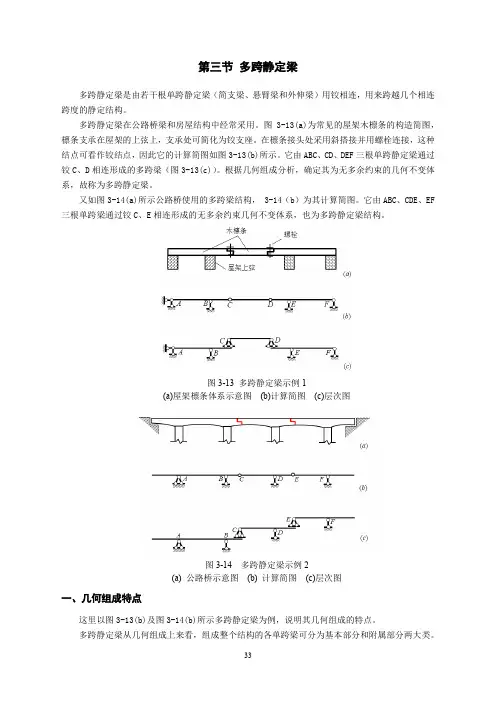
第三节多跨静定梁多跨静定梁是由若干根单跨静定梁（简支梁、悬臂梁和外伸梁）用铰相连，用来跨越几个相连跨度的静定结构。

多跨静定梁在公路桥梁和房屋结构中经常采用。

图3-13(a)为常见的屋架木檩条的构造简图，檩条支承在屋架的上弦上，支承处可简化为铰支座。

在檩条接头处采用斜搭接并用螺栓连接，这种结点可看作铰结点，因此它的计算简图如图3-13(b)所示。

它由ABC、CD、DEF三根单跨静定梁通过铰C、D相连形成的多跨梁（图3-13(c)）。

根据几何组成分析，确定其为无多余约束的几何不变体系，故称为多跨静定梁。

又如图3-14(a)所示公路桥使用的多跨梁结构， 3-14（b）为其计算简图。

它由ABC、CDE、EF 三根单跨梁通过铰C、E相连形成的无多余约束几何不变体系，也为多跨静定梁结构。

图3-13 多跨静定梁示例1(a)屋架檩条体系示意图(b)计算简图(c)层次图图3-14 多跨静定梁示例2(a) 公路桥示意图(b) 计算简图(c)层次图一、几何组成特点这里以图3-13(b)及图3-14(b)所示多跨静定梁为例，说明其几何组成的特点。

多跨静定梁从几何组成上来看，组成整个结构的各单跨梁可分为基本部分和附属部分两大类。

基本部分是指本身能独立维持平衡的部分，而需要依靠其他部分的支承才能保持平衡的部分称为附属部分。

因此，多跨静定梁从几何组成上来看见，是先固定基本部分，再固定附属部分。

如图3-13(b)中多跨静定梁，梁段ABC 由三根不平行也不交于一点的三根链杆固定于基础，它不依赖于其他部分就能独立维持自身的几何不变性；梁段DEF 虽然只有两根链杆与基础相连，但在竖向荷载作用下自身也能维持平衡。

因此，梁段ABC 、梁段DEF 均为基本部分。

而梁段CD 支承于前述两个基本部分上，它必须依赖于梁段ABC 、梁段DEF 才能保持几何不变，所以是附属部分。

为了更清楚地表明多跨静定梁中各梁段之间的支承关系，常把基本部分画在附属部分的下方，附属部分画在基本部分的上方，如图3-13(c)所示，称为层次图。

1 结构力学多媒体课件◆几何特性：无多余约束的几何不变体系◆静力特征：仅由静力平衡条件可求全部反力和内力◆常见静定结构：梁、刚架、三铰拱、桁架和组合结构。

◆静定结构受力分析的内容：反力和内力的计算，内力图的绘制和受力性能分析。

◆静定结构受力分析的基本方法：选取脱离体，建立平衡方程。

◆注意静力分析（拆）与构造分析（搭）的联系◆学习中应注意的问题：多思考,勤动手。

本章是后面学习的基础，十分重要,要熟练掌握！容易产生的错误认识：“静定结构内力分析无非就是选取隔离体，建立平衡方程，以前早就学过了，没有新东西”一、反力的计算4kN1kN/mDCBA2m2m 4mCB A20kN/m 4m4m2m6mDCB A（1）上部结构与基础的联系为3个时，对整体利用3个平衡方程，就可求得反力。

（2）上部结构与基础的联系多于三个时，不仅要对 整体建立平衡方程，而且必须把结构打开， 取隔离体补充方程。

1、内力分量及正负规定轴力F N ：截面上应力沿杆轴法线方向的合力。

以拉力为正，压力为负。

剪力F Q ：截面上应力沿杆轴切线方向的合力。

以绕隔离体顺时针转为正,反之为负。

弯矩M ：截面应力对截面中性轴的力矩。

不规定正负，但弯矩图画在受拉侧。

在水平杆中， 当弯矩使杆件下部纤维受拉时为正。

A 端B 端杆端内力 F Q ABF N ABM AB正 F N BA F Q BAM BA 正2、内力的计算方法K截面法：截开、代替、平衡。

内力的直接算式(截面内力代数和法)=截面一边所有外力沿截面法线方向投影的代数和。

轴力FN外力背离截面投影取正，反之取负。

剪力F=截面一边所有外力沿截面切线方向投影代数和。

Q外力绕截面形心顺时针转动，投影取正，反之取负。

弯矩M =截面一边所有外力对截面形心的外力矩之和。

外力矩和弯矩使杆同侧受拉时取正，反之取负。

2、内力的计算方法【例】如图所示简支梁，计算截面C 、D 1、D 2的内力。

2m 4m 2mA2kN/mCBD 1 D 210kN0.2m10kN3.75kN0.25kN3、绘制内力图的规定内力图是表示结构上各截面的内力各杆件轴线分布规律的图形， 作图规定：弯矩图一律绘在受拉纤维一侧，图上不注明正负号；剪力图和轴力图可绘在杆轴线的任一侧(对水平杆件通常把正号的剪力和轴力绘于上方)，但必须注明正负号，且正负不能绘在同一侧。

多跨铰接连续静定梁内力分析第1跨内力分析：R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i )，i=1 M i =qL i 2*[1-(A i /L i )2]2/8，i=1 第2跨内力分析： P i =R Bi-1，i=2R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i )，i=2M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ]，i=2 M A2=-(P i *A i +qA i 2/2)，(i=2) 第3跨内力分析：P i =R Bi-1，i=3R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i )，i=3M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ]，i=3 M A3=-(P i *A i +qA i 2/2)，(i=3) 第4跨内力分析：P i =R Bi-1，i=4R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i )，i=4M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ]，i=4 M A4=-(P i *A i +qA i 2/2)，(i=4) 第5跨内力分析： P i =R Bi-1，i=5R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i )，i=5M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ]，i=5 M A5=-(P i *A i +qA i 2/2)，(i=5) 第6跨内力分析： P i =R Bi-1，i=6R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i )，i=6M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ]，i=6 M A6=-(P i *A i +qA i 2/2)，(i=6) 第7跨内力分析： P i =R Bi-1，i=7R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i )，i=7M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ]，i=7 M A7=-(P i *A i +qA i 2/2)，(i=7) 第8跨内力分析： P i =R Bi-1，i=8R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i )，i=8M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ]，i=8 M A8=-(P i *A i +qA i 2/2)，(i=8) 第9跨内力分析： P i =R Bi-1，i=9R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i )，i=9M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ]，i=9 M A9=-(P i *A i +qA i 2/2)，(i=9)第10跨内力分析： P i =R Bi-1，i=10R Bi =qL i *[1-(A i /L i )2]/2-P i *(A i /L i )，i=10M i =qL i 2*[1-(A i /L i )2]2/8-P i *A i *[1-(1+(A i /L i ))2/2+A i /L i ]，i=10 M A10=-(P i *A i +qA i 2/2)，(i=10)希望以上资料对你有所帮助，附励志名言3条： 1、理想的路总是为有信心的人预备着。

内力的概念和表示在平面杆件的任意截面上，将内力一般分为三个分量：轴力F N 、剪力F Q 和弯矩MM A轴力----截面上应力沿杆轴切线方向的合力。

轴力以拉力为正。

剪力----截面上应力沿杆轴法线方向的合力。

剪力以绕微段隔离体顺时针转者为正。

内力的概念和表示弯矩----截面上应力对截面形心的力矩。

在水平杆件中，当弯矩使杆件下部受拉时，弯矩为正。

作图时，轴力图和剪力图要注明正负号，弯矩图规定画在杆件受拉的一侧，不用注明正负号。

内力的计算方法梁的内力的计算方法主要采用截面法。

截面法可用“截开、代替、平衡”六个字来描述：1.截开----在所求内力的截面处截开，任取一部分作为隔离体；隔离体与其周围的约束要全部截断。

2.代替----用截面内力代替该截面的应力之和；用相应的约束力代替截断约束。

3.平衡----利用隔离体的平衡条件，确定该截面的内力。

内力的计算方法利用截面法可得出以下结论：1.轴力等于截面一边的所有外力沿杆轴切线方向的投影代数和；2.剪力等于截面一边所有外力沿杆轴法线方向的投影代数和；3.弯矩等于截面一边所有外力对截面形心力矩的代数和。

以上结论是解决静定结构内力的关键和规律，应熟练掌握和应用。

分段叠加法画弯矩图1.叠加原理：几个力对杆件的作用效果，等于每一个力单独作用效果的总和。

= +=+2.分段叠加原理：上述叠加法同样可用于绘制结构中任意直杆段的弯矩图。

例例：下图为一简支梁，AB段的弯矩可以用叠加法进行计算。

（1）（2）（3）（4）静定多跨连续梁的实例现实生活中，一些梁是由几根短梁用榫接相连而成，在力学中可以将榫接简化成铰约束,这样由几个单跨梁组成几何不变体系，称作为静定多跨连续梁。

下图为简化的静定多跨连续梁。

静定多跨梁的受力特点结构特点：图中AB依靠自身就能保持其几何不变性的部分称为基本部分，如图中AB；而必须依靠基本部分才能维持其几何不变性的部分称为附属部分，如图中CD。

受力特点：作用在基本部分的力不影响附属部分，作用在附属部分的力反过来影响基本部分。

王飞教师结构力学课程第4 讲（单元）教案设计第三章静定结构的受力分析1. 静定结构的概念从几何构造分析的角度看，结构必须是几何不变体系。

根据多余约束n，几何不变体系又分为：有多余约束( n > 0)的几何不变体系——超静定结构；无多余约束( n = 0)的几何不变体系——静定结构。

从求解内力和反力的方法也可以认为：静定结构：凡只需要利用静力平衡条件就能计算出结构的全部支座反力和杆件内力的结构。

超静定结构：若结构的全部支座反力和杆件内力，不能只有静力平衡条件来确定的结构。

静定结构的基本特点是l 在几何组成上，静定结构是无多余联系的几何不变体系。

2 在静力学上，静定结构的所有反力、内力仅由静力平衡方程即可求得，且在荷载作用下，解答具有唯一性。

3 静定结构只在荷载作用下才产生反力、内力。

反力和内力只与结构的尺寸、几何形状有关，而与构件截面尺寸、形状、材料无关，且支座沉陷、温度变化、制造误差等均不会产生内力，只产生位移。

§3-1 梁的内力计算回顾3.1.1 内力的概念和表示在平面杆件的任意截面上，将内力一般分为三个分量：轴力F N、剪力F Q和弯矩M(图3-1)。

轴力----截面上应力沿轴线方向的合力,轴力以拉力为正。

剪力----截面上应力沿杆轴法线方向的合力,剪力以截开部分顺时针转向为正。

弯矩----截面上应力对截面形心的力矩，在水平杆件中，当弯矩使杆件下部受拉时弯矩为正。

图3-1作图时，轴力图、剪力图要注明正负号，弯矩图规定画在杆件受拉的一侧，不用注明正负号3.1.2 内力的计算方法梁的内力的计算方法主要采用截面法。

截面法可用以下六个字描述：1. 截开----在所求内力的截面处截开，任取一部分作为隔离体。

2. 代替----用相应内力代替该截面的应力之和。

3. 平衡----利用隔离体的平衡条件，确定该截面的内力。

利用截面法可得出以下结论：1. 轴力等于该截面一侧所有的外力沿杆轴切线方向的投影代数和；2. 剪力等于该截面一侧所有外力沿杆轴法线方向的投影代数和；3. 弯矩等于该截面一侧所有外力对截面形心的力矩的代数和。