分析多跨静定梁的步骤(精)
- 格式:doc
- 大小:696.00 KB
- 文档页数:2






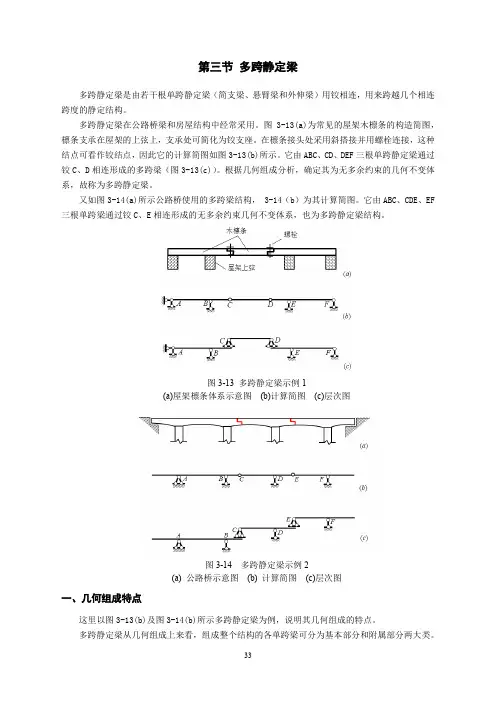
第三节多跨静定梁多跨静定梁是由若干根单跨静定梁(简支梁、悬臂梁和外伸梁)用铰相连,用来跨越几个相连跨度的静定结构。
多跨静定梁在公路桥梁和房屋结构中经常采用。
图3-13(a)为常见的屋架木檩条的构造简图,檩条支承在屋架的上弦上,支承处可简化为铰支座。
在檩条接头处采用斜搭接并用螺栓连接,这种结点可看作铰结点,因此它的计算简图如图3-13(b)所示。
它由ABC、CD、DEF三根单跨静定梁通过铰C、D相连形成的多跨梁(图3-13(c))。
根据几何组成分析,确定其为无多余约束的几何不变体系,故称为多跨静定梁。
又如图3-14(a)所示公路桥使用的多跨梁结构, 3-14(b)为其计算简图。
它由ABC、CDE、EF 三根单跨梁通过铰C、E相连形成的无多余约束几何不变体系,也为多跨静定梁结构。
图3-13 多跨静定梁示例1(a)屋架檩条体系示意图(b)计算简图(c)层次图图3-14 多跨静定梁示例2(a) 公路桥示意图(b) 计算简图(c)层次图一、几何组成特点这里以图3-13(b)及图3-14(b)所示多跨静定梁为例,说明其几何组成的特点。
多跨静定梁从几何组成上来看,组成整个结构的各单跨梁可分为基本部分和附属部分两大类。
基本部分是指本身能独立维持平衡的部分,而需要依靠其他部分的支承才能保持平衡的部分称为附属部分。
因此,多跨静定梁从几何组成上来看见,是先固定基本部分,再固定附属部分。
如图3-13(b)中多跨静定梁,梁段ABC 由三根不平行也不交于一点的三根链杆固定于基础,它不依赖于其他部分就能独立维持自身的几何不变性;梁段DEF 虽然只有两根链杆与基础相连,但在竖向荷载作用下自身也能维持平衡。
因此,梁段ABC 、梁段DEF 均为基本部分。
而梁段CD 支承于前述两个基本部分上,它必须依赖于梁段ABC 、梁段DEF 才能保持几何不变,所以是附属部分。
为了更清楚地表明多跨静定梁中各梁段之间的支承关系,常把基本部分画在附属部分的下方,附属部分画在基本部分的上方,如图3-13(c)所示,称为层次图。



计算多跨静定梁时,可以按照以下步骤进行计算顺序:
1. 确定梁的支座类型和位置:首先确定梁的支座类型,例如固定支座、铰支座或滑动
支座,并确定它们的位置。
2. 划分梁的跨数:根据实际情况,将梁划分为多个跨。
3. 确定每个跨的边界条件:对于每个跨,确定其边界条件,如支座反力、弯矩、剪力等。
4. 单独计算每个跨的内力:对于每个跨,使用适当的方法(如力法、位移法或弯矩法)计算其内力分布。
5. 跨间连续性条件的处理:对于相邻的两个跨,考虑它们之间的连续性条件,例如弯
矩连续性条件。
6. 解算未知反力:根据边界条件和连续性条件,解算出所有跨的未知反力。
7. 检验静定条件:检查所得到的反力是否符合静定条件,即受力平衡和变形平衡。
8. 计算梁的内力分布:根据已知的反力和边界条件,计算梁的内力分布,如弯矩、剪
力和轴力。
9. 校验计算结果:检查计算结果是否满足设计要求,如强度、刚度和稳定性等。
请注意,以上仅为一般情况下多跨静定梁计算的顺序,具体问题具体分析,可能需要
根据实际情况进行调整。
同时,如果你有特定的问题或需要更详细的计算步骤,请提
供更多信息,我将尽力提供帮助。

多跨静定与超静定梁力学性能对比实验结果分析与讨
论
本文将对跨静定与超静定梁的力学性能进行实验结果分析与讨论。
跨静定梁是指具有多个支座的梁结构,而超静定梁是指具有多余支座的梁结构。
实验结果显示,在相同荷载条件下,跨静定梁与超静定梁的力学性能存在一定的差异。
首先,跨静定梁的变形能力较差,当荷载增加时,梁的变形会逐渐增大,可能导致梁的破坏。
而超静定梁具有较好的变形能力,可以在承受更大的荷载时保持较小的变形。
跨静定梁的应力分布较为集中,容易出现局部应力过大的情况,从而增加梁的破坏风险。
而超静定梁的应力分布相对均匀,能够更好地分散荷载,并减小应力集中的可能。
跨静定梁与超静定梁在破坏模式上也存在差异。
跨静定梁一般会以某个支座处的破坏为主,而超静定梁则可能在多个支座处出现破坏。
这意味着超静定梁具有更好的破坏韧性,能够在某个支座破坏后仍保持一定的承载能力。
跨静定梁与超静定梁在力学性能上存在明显的差异,超静定梁具有较好的变形能力、应力分布均匀以及较好的破坏韧性,适用于需要承受较大荷载并保持结构稳定的工程项目。
而跨静定梁则适用于对变形和应力分布要求较低的项目。
超静定多跨梁的计算吴郁斌力法的原理及二次超静定多跨梁的计算思路力法是计算超静定结构的最基本的方法。
采用力法解决超静定结构问题时,不是孤立地研究超静定问题,而是把超静定问题与静定问题联系起来,加以比较,从而把超静定结构问题转化为静定结构问题来加以解决。
在解决超静定多跨梁结构问题时,首先要确定超静定的次数,如下图所示:图一图一所示的静定多跨梁中,经分析得知,结构中的B 、C 两点的约束为多余约束,所以该结构为二次超静定问题。
其次,在确定超静定次数之后,按力学方法对模型进行转化,将超静定结构转变为静定结构。
在图一所示的结构中,我们先假设B 、C 两点无约束,而作用两个集中力C B F F 、,方向按图一所示,这样我们就把一个超静定多跨梁结构转化成简支梁结构,从而把解决超静定多跨梁结构的问题也转化成解决简支梁的问题。
最后,找出结构转化过程中的限制条件,按照条件列出力法方程。
在图一所示的结构中,当我们把超静定多跨梁结构转化成简支梁的过程中,我们必须限制B 、C 两点的竖向位移为0,因为在原来的超静定多跨梁结构中,B 、C 两点有约束。
然后根据限制条件列出力法方程。
假设作用于多跨梁上的载荷在B 、C 两点产生的竖向位移分别为1∆和2∆,作用于B 点的单位竖向力(即当1=B F 时)在B 、C 两点产生的竖向位移分别为1211δδ和,作用于C 点的单位竖向力(即当1=C F 时)在B 、C 两点产生的竖向位移分别为21δ和22δ。
设作用于B 、C 两点的实际作用力大小分别为倍的单位力、21X X 。
我们都知道梁的位移与载荷的大小成正比,所以根据限制条件以及假设条件,可以列出如下方程:⎩⎨⎧=∆-⋅+⋅=∆-⋅+⋅0022221211212111X X X X δδδδ 通过上述方程就可以计算出B 、C 两点的支座反力C B F F 、,然后通过力平衡方程和弯矩平衡方程就可以解出两外两点(A 、D 两点)的支座反力,即⎪⎩⎪⎨⎧==∑∑00y A M F ,⇒()⎩⎨⎧=⋅+⋅-+⋅+⋅=+++0a 0211y L F F L L F L F F F F F D C B D C B A 解之,就可以得到各个支座的反力,进而得到梁上各段的剪力图和弯矩图了。
分析多跨静定梁的步骤
计算多跨静定梁的步骤可归纳为以下三步:
(1)先对结构进行几何组成分析,按几何组成分析中刚片的选取次序确定基本部分和附属部分,作出层次图。
(2)根据所作层次图,从上层向下层依次取研究对象,计算各梁的约束力。
(3)按照作单跨梁内力图的方法,分别作出各梁段的内力图,然后再按原顺序连接在一起,即得多跨静定梁的内力图。
例题作如图(a)所示多跨静定梁的剪力图和弯矩图。
解:(1)进行几何组成分析并作层次图。
选地基为刚片Ⅰ,ABE梁为刚片Ⅱ,FCD 梁为刚片Ⅲ。
几何组成分析如下:
作层次图如图(b)所示
(2)计算约束力。
先取EF梁为研究对象,再取FCD梁为研究对象,后取ABE梁为研究对象。
例题图(c)所示为各梁段的受力图。
应用平衡条件依次求出各梁的约束力。
求解过程这里不再详述。
将所求得的各约束反力值标在受力图中。
(3)作内力图。
根据各梁的荷载及约束力情况,分别画出各梁段的剪力图和弯矩图,最后分别把它们按原顺序连在一起。
多跨静定梁的剪力图和弯矩图如图(d)、(e)所示。
例题图。