第四章第二讲子博弈精炼纳什均衡

子博弈纳什均衡
《子博弈纳什均衡》是一种博弈理论，它是由美国数学家纳什提出的。

它的核心思想是，博弈双方应该通过分析双方的策略，使双方的利益最大化，从而达到一个均衡点。

这种均衡点又被称为“纳什均衡”。

纳什均衡是一种抉择，它反映了双方可以通过分析双方的策略，使双方的利益最大化，从而达到一个均衡点，使双方的利益最大化。

它的特点是双方的行动是互相制约的，一方的行动会影响另一方的行动，双方都会尽量获得最大的利益。

纳什均衡的应用非常广泛，它可以用于经济学、政治学、军事学等多个领域，可以用来分析和解决各种博弈问题。

它的核心思想是，双方应该通过分析双方的策略，使双方的利益最大化，从而达到一个均衡点。

纳什均衡是一种博弈理论，它有助于双方在博弈中达成和谐、公平的结果，从而使双方都能获得最大的利益。

它的应用非常广泛，可以用于经济学、政治学、军事学等多个领域，是一种有效的博弈理论。

子博弈完美纳什均衡
“子博弈精炼纳什均衡”的创立者是1994年诺贝尔经济学奖获奖者、莱茵哈德·泽尔腾。

泽尔腾则在60年代中期将纳什均衡概念引入动态分析。

在1965年发表《需求减少条件下寡头垄断模型的对策论描述》一文，提出了“子博弈精炼纳什均衡”的概念，又称“子对策完美纳什均衡”。

这一研究对纳什均衡进行了第一次改进，选择了更具说服力的均衡点。

海萨尼在60年代末把不完全信息引入博弈分析。

子博弈精炼纳什均衡用于区分动态博弈中的"合理纳什均衡"与"不合理纳什均衡"，将纳什均衡中包含有不可置信威胁策略的均衡剔除出去，就是说，使最后的均衡中不再包含有不可置信威胁策略的存在。

子博弈精炼纳什均衡的基本概念在动态博弈中，行动有先后次序，后行动者可以通过观察先行动者的行为，来获得有关先行动者的信息，从而证实或修正自己对先行动者的判断。

完全信息动态博弈，是指博弈中信息是完全的，即双方都掌握参与者对他参与人的战略空间和战略组合下的支付函数有完全的了解，但行动是有先后顺序的，后动者可以观察到前者的行动，了解前者行动的所有信息。

在不完全信息静态博弈中，参与人同时行动，没有机会观察到别人的选择。

而在不完全信息动态博弈中，问题变得更加简单。

博弈开始时，某一参与人既不知道其他参与人的真实类型，也不知道其他参与人所属类型的分布概率。

他只是对这一概率分布有自己的主观判断，即有自己的信念。

博弈开始后，该参与人将根据他所观察到的其他参与人的行为，来修正自己的信念。

并根据这种不断变化的信念，作出自己的战略选择。

动态博弈行动有先后顺序，不同的参与人在不同时点行动，先行动者的选择影响后行动者的选择空间，后行动者可以观察到先行动者做了什么选择，因此，为了做最优的行动选择，每个参与人都必须这样思考问题：如果我如此选择，对方将如何应对？如果我是他，我将会如何行动？给定他的应对，什么是我的最优选择？如下棋。

[1]子博弈精炼纳什均衡包含两层含义:（1）它是原博弈的纳什均衡；（2）它在每一个子博弈上给出纳什均衡。

子博弈精炼纳什均衡就是要剔除那些只在特定情况下是合理的，而在其他情况下并不合理的行动规则在动态博弈中，参与人的行动有先后顺序，后行动的参与人在自己行动之前就可以观察到先行动者（参与人）的行为，并在此基础上选择相应的策略。

而且，由于先行动者拥有后行动者可能选择策略的完全信息，因而先行动者在选择自己的策略时，就可以预先考虑自己的选择对后行动者选择的影响，并采取相应的对策。

子博弈是指在动态博弈中，所有参与人先后都采取了一次行动后所构成的一组新的博弈，这组博弈中的每一个都称为“子博弈”。

当只当参与人的战略在其子博弈的系列（第二代、第三代…）中，每一个子博弈都构成纳什均衡，就构成了子博弈精练纳什均衡子博弈子博弈（Subgame）[编辑]什么是子博弈子博弈是指在动态博弈中，所有参与人先后都采取了一次行动后所构成的一组新的博弈，这组博弈中的每一个都称为“子博弈”。

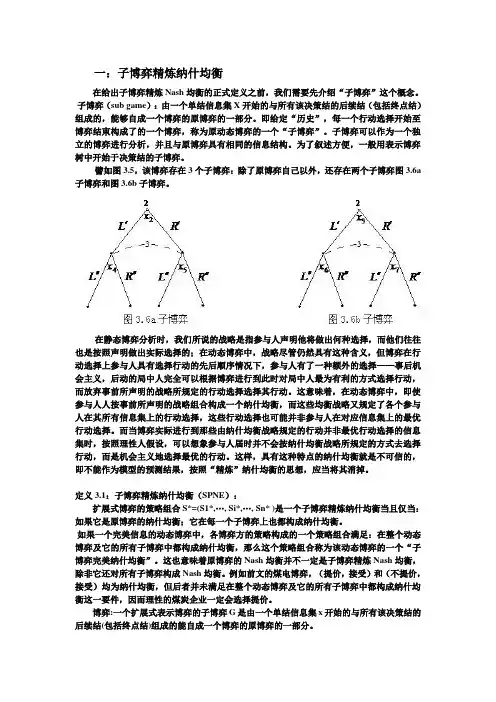
一：子博弈精炼纳什均衡在给出子博弈精炼Nash均衡的正式定义之前，我们需要先介绍“子博弈”这个概念。

子博弈（sub game）：由一个单结信息集X开始的与所有该决策结的后续结（包括终点结）组成的，能够自成一个博弈的原博弈的一部分。

即给定“历史”，每一个行动选择开始至博弈结束构成了的一个博弈，称为原动态博弈的一个“子博弈”。

子博弈可以作为一个独立的博弈进行分析，并且与原博弈具有相同的信息结构。

为了叙述方便，一般用表示博弈树中开始于决策结的子博弈。

譬如图3.5，该博弈存在3个子博弈：除了原博弈自己以外，还存在两个子博弈图3.6a 子博弈和图3.6b子博弈。

在静态博弈分析时，我们所说的战略是指参与人声明他将做出何种选择，而他们往往也是按照声明做出实际选择的；在动态博弈中，战略尽管仍然具有这种含义，但博弈在行动选择上参与人具有选择行动的先后顺序情况下，参与人有了一种额外的选择——事后机会主义，后动的局中人完全可以根据博弈进行到此时对局中人最为有利的方式选择行动，而放弃事前所声明的战略所规定的行动选择选择其行动。

这意味着，在动态博弈中，即使参与人人按事前所声明的战略组合构成一个纳什均衡，而这些均衡战略又规定了各个参与人在其所有信息集上的行动选择，这些行动选择也可能并非参与人在对应信息集上的最优行动选择。

而当博弈实际进行到那些由纳什均衡战略规定的行动并非最优行动选择的信息集时，按照理性人假设，可以想象参与人届时并不会按纳什均衡战略所规定的方式去选择行动，而是机会主义地选择最优的行动。

这样，具有这种特点的纳什均衡就是不可信的，即不能作为模型的预测结果，按照“精炼”纳什均衡的思想，应当将其消掉。

定义3.1：子博弈精炼纳什均衡（SPNE）：扩展式博弈的策略组合 S*=(S1*,…, Si*,…, Sn* )是一个子博弈精炼纳什均衡当且仅当：如果它是原博弈的纳什均衡；它在每一个子博弈上也都构成纳什均衡。

如果一个完美信息的动态博弈中，各博弈方的策略构成的一个策略组合满足：在整个动态博弈及它的所有子博弈中都构成纳什均衡，那么这个策略组合称为该动态博弈的一个“子博弈完美纳什均衡”。

子博弈计算
子博弈精炼纳什均衡（Subgame Perfect Nash Equilibrium，SPNE）是一种均衡策略，它在所有子博弈中都是最优的。

它是纳什均衡的精炼，也就是说，如果一个策略组合是纳什均衡，并且它在所有子博弈中都是最优的，那么它就是子博弈精炼纳什均衡。

在计算子博弈精炼纳什均衡时，需要先确定博弈的子博弈。

子博弈是原博弈的一部分，它包含了原博弈中的某些信息集和行动。

然后，在这些子博弈中，寻找最优的策略组合，使得每个参与者在每个子博弈中都能够获得最优的结果。

具体来说，计算子博弈精炼纳什均衡的步骤如下：
确定博弈的子博弈。

这可以通过分析博弈的信息集和行动来实现。

对于每个子博弈，分别计算每个参与者的最优策略。

这可以通过求解子博弈中的最优策略问题来实现。

如果存在多个最优策略，则需要比较它们的预期收益。

选择预期收益最高的策略作为子博弈精炼纳什均衡。

重复以上步骤，直到所有子博弈都找到最优策略。

需要注意的是，子博弈精炼纳什均衡的计算可能需要较高的计算能力和技巧。

因此，在实际应用中，可能需要借助计算机软件或算法来求解子博弈精炼纳什均衡。

此外，子博弈精炼纳什均衡是一种理想化的均衡概念，它假设每个参与者在每个子博弈中都能够理性地选择最优策略。

但在实际情况下，参与者的行为可能会受到各种因素的影响，使得他们无法总是选择最优策略。

因此，在实际应用中，需要考虑参与者的行为特征和限制，并在此基础上进行均衡分析和计算。

子博弈精炼纳什均衡名词解释嘿，朋友们！今天咱来聊聊子博弈精炼纳什均衡这个听起来有点高大上的玩意儿。

你看啊，这就好比是一场复杂的游戏。

在这个游戏里，每个人都有自己的策略和选择。

子博弈精炼纳什均衡呢，就是在这个游戏中的某个局部，大家都找到了一个最佳的玩法，谁也不愿意轻易改变。

咱可以想象一下，一群人在玩扑克牌，每个人都在算计着怎么出牌才能赢。

在某个特定的局面下，大家都形成了一种默契，都按照某种特定的方式出牌，因为这样对自己最有利呀。

这就是一种子博弈精炼纳什均衡。

它可不是随随便便就能达到的哦！就像爬山一样，得一步一步找到最合适的路径。

在这个过程中，大家都得不断地思考、算计，权衡各种利弊。

而且啊，它还很稳定呢，一旦达到了，就不太容易被打破。

比如说在商业竞争中，几家公司在市场上争斗。

他们会根据对手的行动来调整自己的策略，直到找到一个大家都觉得不错的状态，这其实就是一种子博弈精炼纳什均衡啦。

再想想下棋，每一步棋都是在追求一种平衡和最优解。

高手下棋的时候，不就是在寻找那个子博弈精炼纳什均衡嘛！他们可不会瞎走，都是深思熟虑的呀。

那这个子博弈精炼纳什均衡有啥用呢？用处可大啦！它能帮我们更好地理解人与人之间的互动和竞争。

知道了这个，我们就能在各种情况下做出更明智的选择。

比如说在谈判的时候，如果你能理解对方的策略，找到那个子博弈精炼纳什均衡，不就能更好地达成自己的目的了嘛！在团队合作中也是一样，大家找到共同的最优策略，工作就能更顺利地进行呀。

总之，子博弈精炼纳什均衡就像是一个隐藏在各种复杂局面背后的秘密武器。

只要我们能发现它、理解它、运用它，就能在生活和工作中更加得心应手。

难道不是吗？所以啊，大家可得好好琢磨琢磨这个有趣的概念哦！。

子博弈精炼纳什均衡●将纳什均衡中包含的不可置信的威胁策略剔除出去。

它要求参与者的决策在任何时点上都是最优的，决策者要“随机应变”，“向前看”，而不是固守旧略。

●由于剔除了不可置信的威胁，在许多情况下，精炼纳什均衡也就缩小了纳什均衡的个数。

这一点对预测分析是非常有意义的。

与纳什均衡的区别●在纳什均衡中，参与人在选择自己战略时，把其他参与人策略当作给定的，不考虑自己的选择将如何影响对手的策略。

●实际上，当一个人行动在前，另一个人行动在后时，后者自然会根据前者的选择而调整自己的选择，前者在作选择时自然会理性地考虑这一点，所以不可能不考虑自己的选择对其对手选择的影响。

博弈表达的标准型与扩展型●博弈的标准型表达有三个要素：参与人，可选择策略及支付函数。

•两人有限策略博弈的标准型可用一个矩阵表来表示。

●扩展型表达包括五个要素：•（1）参与人；（2）每个参与人选择行动的时点；（3）每个参与人在每次行动时可供选择的行动集合；（4）每个参与人在每次行动时有关对手过去行动选择的信息；（5）支付函数。

市场进入阻挠博弈●假设一个企业A是市场上的唯一供给者，面临企业B可能的竞争威胁。

企业A有两种可选策略，即斗争与默许。

斗争表现为采用降低价格使B的收益为0，默许意味着维持高价格。

企业B也有两种策略：进入或者不进入。

假定进入之前垄断利润为300，进入之后寡头利润共为100（各得50），进入成本是10。

各种策略组合下的支付矩阵如下表：举例分析●该博弈显然有两个纳什均衡，即（进入，高价），（不进入，低价）。

●静态分析方法，得到两个纳什均衡。

分析●给定企业B进入的话，企业A选择高价时得50利润，选择低价时得不到利润，所以最优战略是高价（默许）。

同理，给定企业A高价时，进入策略成为企业B最优选择。

尽管在企业B 选择不进入时，企业A采取任何一种策略都是一样得，但只有当企业A选择低价时，不进入才是企业B的最优选择，所以（不进入，低价）也是一个纳什均衡，而（不进入，高价）不是纳什均衡。