子博弈精炼Nash均衡

子博弈完美纳什均衡
“子博弈精炼纳什均衡”的创立者是1994年诺贝尔经济学奖获奖者、莱茵哈德·泽尔腾。

泽尔腾则在60年代中期将纳什均衡概念引入动态分析。

在1965年发表《需求减少条件下寡头垄断模型的对策论描述》一文，提出了“子博弈精炼纳什均衡”的概念，又称“子对策完美纳什均衡”。

这一研究对纳什均衡进行了第一次改进，选择了更具说服力的均衡点。

海萨尼在60年代末把不完全信息引入博弈分析。

子博弈精炼纳什均衡用于区分动态博弈中的"合理纳什均衡"与"不合理纳什均衡"，将纳什均衡中包含有不可置信威胁策略的均衡剔除出去，就是说，使最后的均衡中不再包含有不可置信威胁策略的存在。

子博弈精炼纳什均衡坏孩子例题摘要：1.子博弈精炼纳什均衡的概念2.子博弈精炼纳什均衡的创立者3.子博弈精炼纳什均衡的例子4.子博弈精炼纳什均衡的应用正文：一、子博弈精炼纳什均衡的概念子博弈精炼纳什均衡（Subgame Perfect Nash Equilibrium）是一种在完全信息动态博弈中求解纳什均衡的方法。

它是由1994 年诺贝尔经济学奖获奖者、莱茵哈德·泽尔腾（Reinhard Selten）在20 世纪60 年代中期提出的。

泽尔腾将纳什均衡概念引入动态分析，为求解动态博弈问题提供了一种有效的工具。

二、子博弈精炼纳什均衡的创立者子博弈精炼纳什均衡的创立者是莱茵哈德·泽尔腾。

他在1965 年发表的《需求减少条件下寡头垄断模型》一文中，首次提出了这一概念。

在此基础上，泽尔腾对动态博弈进行了深入研究，并因此荣获1994 年诺贝尔经济学奖。

三、子博弈精炼纳什均衡的例子为了更好地理解子博弈精炼纳什均衡，我们可以通过一个例子来说明。

假设有两个玩家A 和B，他们要决定是否合作完成一个任务。

任务的完成需要两个玩家的共同努力，如果两人都努力，则任务完成概率高；如果只有一个人努力，则任务完成概率较低。

玩家A 和B 都可以选择努力或不努力。

在这个例子中，子博弈精炼纳什均衡的解为：A 和B 都努力。

这是因为，如果A 努力而B 不努力，那么任务很难完成，A 的收益会受到影响；同样，如果B 努力而A 不努力，任务也很难完成，B 的收益会受到影响。

因此，A 和B 都会选择努力，这样任务才能顺利完成，双方收益最大。

四、子博弈精炼纳什均衡的应用子博弈精炼纳什均衡在经济学、社会学、政治学等领域具有广泛的应用。

例如，在拍卖市场中，竞拍者可以通过子博弈精炼纳什均衡来确定最佳的竞拍策略；在劳资谈判中，雇主和工会可以通过子博弈精炼纳什均衡来达成最有利于双方的协议。

子博弈精炼纳什均衡的基本概念在动态博弈中，行动有先后次序，后行动者可以通过观察先行动者的行为，来获得有关先行动者的信息，从而证实或修正自己对先行动者的判断。

完全信息动态博弈，是指博弈中信息是完全的，即双方都掌握参与者对他参与人的战略空间和战略组合下的支付函数有完全的了解，但行动是有先后顺序的，后动者可以观察到前者的行动，了解前者行动的所有信息。

在不完全信息静态博弈中，参与人同时行动，没有机会观察到别人的选择。

而在不完全信息动态博弈中，问题变得更加简单。

博弈开始时，某一参与人既不知道其他参与人的真实类型，也不知道其他参与人所属类型的分布概率。

他只是对这一概率分布有自己的主观判断，即有自己的信念。

博弈开始后，该参与人将根据他所观察到的其他参与人的行为，来修正自己的信念。

并根据这种不断变化的信念，作出自己的战略选择。

动态博弈行动有先后顺序，不同的参与人在不同时点行动，先行动者的选择影响后行动者的选择空间，后行动者可以观察到先行动者做了什么选择，因此，为了做最优的行动选择，每个参与人都必须这样思考问题：如果我如此选择，对方将如何应对？如果我是他，我将会如何行动？给定他的应对，什么是我的最优选择？如下棋。

[1]子博弈精炼纳什均衡包含两层含义:（1）它是原博弈的纳什均衡；（2）它在每一个子博弈上给出纳什均衡。

子博弈精炼纳什均衡就是要剔除那些只在特定情况下是合理的，而在其他情况下并不合理的行动规则在动态博弈中，参与人的行动有先后顺序，后行动的参与人在自己行动之前就可以观察到先行动者（参与人）的行为，并在此基础上选择相应的策略。

而且，由于先行动者拥有后行动者可能选择策略的完全信息，因而先行动者在选择自己的策略时，就可以预先考虑自己的选择对后行动者选择的影响，并采取相应的对策。

子博弈是指在动态博弈中，所有参与人先后都采取了一次行动后所构成的一组新的博弈，这组博弈中的每一个都称为“子博弈”。

当只当参与人的战略在其子博弈的系列（第二代、第三代…）中，每一个子博弈都构成纳什均衡，就构成了子博弈精练纳什均衡子博弈子博弈（Subgame）[编辑]什么是子博弈子博弈是指在动态博弈中，所有参与人先后都采取了一次行动后所构成的一组新的博弈，这组博弈中的每一个都称为“子博弈”。

我们已经了解了完全信息静态博弈的内容。

这时候，参与人同时行动，或者不同时行动，但是后动的人观察不到先动的人的任何有关其行动的信息，这于同时行动等价。

这时候，任何一个参与人选择行动的时候，没有任何可以依据的信息。

当博弈成为动态的时候，参与人先后行动，后动者可以观察到先动者的行动，因此，后动者选择他的行动的时候，可以依据观察到的信息作选择。

因为先动者可能采取的行动是若干个，所以后动者就有可能观察到同样多的信息。

因此，这时后动者选择的已经不简单的行动，而是一套完整的行动计划——这套行动计划指出，在观察到不同的信息时该怎样随机应变选择自己的行动。

因此，现在后动者的选择变量就是行动计划，我们就把一套完整的行动计划叫做一个策略。

以下图为例，参与人1先动，之后参与人2行动，参与人2可以观察到参与人1的选择。

参与人的选择就是L或者R，这既是他的行动有时他的策略，因为参与人1行动时可能出现的信息只有一种情况——空信息集——因为他先动，这时什么信息也没有。

1行动之后，1的行动可以被2观察，因此2可能观察到的信息就有可能是L或者R，因此，2的行动会根据这些信息作出。

2的一套完整的行动计划应该告诉他，在观察到L时选择什么，观察到R时选择什么，由此我们也可以看出，如果2把行动的选择委托给另外的人，这个人可以根据2的行动计划处理任何可能发生或者面对的形式。

这样，2的行动计划——我们称为策略，就有四种可能：1，观察到L时，选F，观察到R时，选F。

我们用一个有序二维向量（F，F）表示。

2，观察到L时，选F，观察到R时，选C。

我们用一个有序二维向量（F，C）表示。

3，观察到L时，选C，观察到R时，选F。

我们用一个有序二维向量（C，F）表示。

4，观察到L时，选C，观察到R时，选C。

我们用一个有序二维向量（C，C）表示。

总结：参与人1的行动是L或者R，由于是先动，没有信息，所以策略也就是行动。

参与人2的行动是F或者C，由于是后动，有信息，策略是建立在信息上的完整行动——计划，有四个策略：（F，F），（F，C）（C，F）（C，C）。

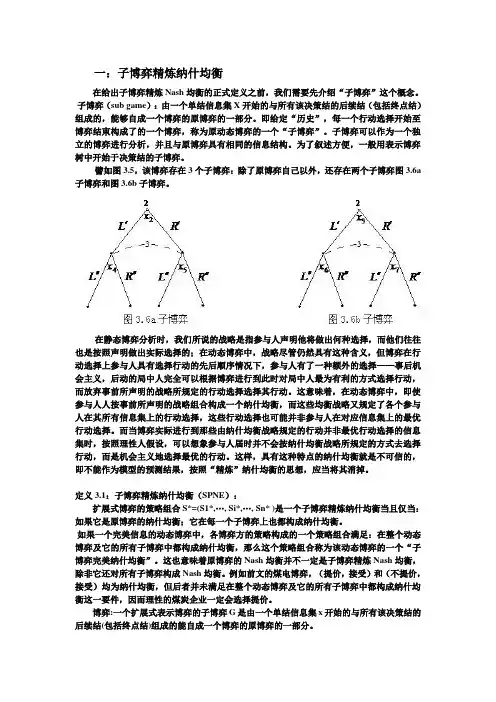
一：子博弈精炼纳什均衡在给出子博弈精炼Nash均衡的正式定义之前，我们需要先介绍“子博弈”这个概念。

子博弈（sub game）：由一个单结信息集X开始的与所有该决策结的后续结（包括终点结）组成的，能够自成一个博弈的原博弈的一部分。

即给定“历史”，每一个行动选择开始至博弈结束构成了的一个博弈，称为原动态博弈的一个“子博弈”。

子博弈可以作为一个独立的博弈进行分析，并且与原博弈具有相同的信息结构。

为了叙述方便，一般用表示博弈树中开始于决策结的子博弈。

譬如图3.5，该博弈存在3个子博弈：除了原博弈自己以外，还存在两个子博弈图3.6a 子博弈和图3.6b子博弈。

在静态博弈分析时，我们所说的战略是指参与人声明他将做出何种选择，而他们往往也是按照声明做出实际选择的；在动态博弈中，战略尽管仍然具有这种含义，但博弈在行动选择上参与人具有选择行动的先后顺序情况下，参与人有了一种额外的选择——事后机会主义，后动的局中人完全可以根据博弈进行到此时对局中人最为有利的方式选择行动，而放弃事前所声明的战略所规定的行动选择选择其行动。

这意味着，在动态博弈中，即使参与人人按事前所声明的战略组合构成一个纳什均衡，而这些均衡战略又规定了各个参与人在其所有信息集上的行动选择，这些行动选择也可能并非参与人在对应信息集上的最优行动选择。

而当博弈实际进行到那些由纳什均衡战略规定的行动并非最优行动选择的信息集时，按照理性人假设，可以想象参与人届时并不会按纳什均衡战略所规定的方式去选择行动，而是机会主义地选择最优的行动。

这样，具有这种特点的纳什均衡就是不可信的，即不能作为模型的预测结果，按照“精炼”纳什均衡的思想，应当将其消掉。

定义3.1：子博弈精炼纳什均衡（SPNE）：扩展式博弈的策略组合 S*=(S1*,…, Si*,…, Sn* )是一个子博弈精炼纳什均衡当且仅当：如果它是原博弈的纳什均衡；它在每一个子博弈上也都构成纳什均衡。

如果一个完美信息的动态博弈中，各博弈方的策略构成的一个策略组合满足：在整个动态博弈及它的所有子博弈中都构成纳什均衡，那么这个策略组合称为该动态博弈的一个“子博弈完美纳什均衡”。

子博弈计算
子博弈精炼纳什均衡（Subgame Perfect Nash Equilibrium，SPNE）是一种均衡策略，它在所有子博弈中都是最优的。

它是纳什均衡的精炼，也就是说，如果一个策略组合是纳什均衡，并且它在所有子博弈中都是最优的，那么它就是子博弈精炼纳什均衡。

在计算子博弈精炼纳什均衡时，需要先确定博弈的子博弈。

子博弈是原博弈的一部分，它包含了原博弈中的某些信息集和行动。

然后，在这些子博弈中，寻找最优的策略组合，使得每个参与者在每个子博弈中都能够获得最优的结果。

具体来说，计算子博弈精炼纳什均衡的步骤如下：
确定博弈的子博弈。

这可以通过分析博弈的信息集和行动来实现。

对于每个子博弈，分别计算每个参与者的最优策略。

这可以通过求解子博弈中的最优策略问题来实现。

如果存在多个最优策略，则需要比较它们的预期收益。

选择预期收益最高的策略作为子博弈精炼纳什均衡。

重复以上步骤，直到所有子博弈都找到最优策略。

需要注意的是，子博弈精炼纳什均衡的计算可能需要较高的计算能力和技巧。

因此，在实际应用中，可能需要借助计算机软件或算法来求解子博弈精炼纳什均衡。

此外，子博弈精炼纳什均衡是一种理想化的均衡概念，它假设每个参与者在每个子博弈中都能够理性地选择最优策略。

但在实际情况下，参与者的行为可能会受到各种因素的影响，使得他们无法总是选择最优策略。

因此，在实际应用中，需要考虑参与者的行为特征和限制，并在此基础上进行均衡分析和计算。

《博弈论：原理、模型与教程》第二部分完全信息动态博弈第7章子博弈精炼Nash均衡7.2 子博弈精炼Nash均衡的求解（重点！）（已精细订正！）定义7－1虽然给出了子博弈精炼Nash的定义，但没有说明如何求解子博弈精炼均Nash衡。

下面以图6－8 中扩展式博弈为例，介绍一种最常用的求解子博弈精炼Nash均衡的方法—逆向归纳法。

（讲！）考察图6－8中的博弈。

参与人1在博弈开始时（即在信息集}{)(11x I 上面临两种选择—行动A 和行动B 。

参与人1此时选择哪种行动呢？对于理性的参与人1来讲，只会选择使自己支付最大化的行动。

从图6－8很容易知道参与人1选择行动B 时所得到的支付为2；但是，如果参与人1选择行动A ，则所得支付就要取决于参与人2在信息集}{)(22x I 上的选择，以及博弈达到决策结3x 时参与人1在信息集}{)(31x I 上的选择。

也就是说，参与人1选择行动A 所得支付，取决于子博弈)(2x Γ的结果。

因此，为了确定参与人1在博弈开始时的选择，就必须确定参与人1选择行动A 的所得支付，而为了确定参与人1选择行动A 的所得支付，就必须先求解子博弈)(2x Γ。

如何求解博弈)(2x Γ呢？可以采用同样的方法来求解子博弈)(2x Γ，即在求解子博弈)(3x Γ的基础上，确定参与人2在信息集}{)(22x I 上的选择，从而求解子博弈)(2x Γ。

由以上分析可以得到图6－8中博弈的求解过程：首先求解博弈树中最底层的子博弈)(3x Γ得到子博弈)(3x Γ的结果为(3,0)（即参与人1选择E ）； 再求解博弈)(2x Γ，容易得到博弈的结果(1,1)（即参与人2选择D ）； 最后求解原博弈，即子博弈)(1x Γ，得到博弈的结果为(2,1)（即参与人1选择B ）。

（讲！）考察更一般的情形。

对于图7－6中的博弈树，参与人i 在信息集})({i i x I 选择行动L 还是行动R ，取决于选择行动L 和行动R 所带来的后果。

《博弈论：原理、模型与教程》第二部分完全信息动态博弈第7章子博弈精炼Nash均衡本章将介绍一种新的博弈的解——子博弈精炼Nash均衡，并对子博弈精炼Nash均衡的唯一性、求解方法及存在的不足进行分析。

7.1 子博弈精炼Nash均衡（已精细订正！）对于扩展式博弈，同样可以用Nash均衡作为博弈的解，但是，与Nash均衡作为战略式博弈的解一样，面临着Nash均衡的多重性问题，而且在多个Nash均衡中有些是明显不合理的。

例如，在图6-1中，博弈存在两个Nash 均衡—))((开发开发开发，，和))((不开发开发开发，，，其中均衡))((不开发开发开发，，要求企业2采取战略“企业1开发自己就开发，企业1不开发自己就不开发”。

在“新产品开发博弈”中，如果市场需求大，不管对方是否开发，每个企业都应该选择“开发”（因为只要开发即可盈利）1 。

所以“当企业1开发时，企业2开发”是合理的；但是当“当企业1不开发时，企业2不开发”是不合理了。

所以，均衡))((不开发开发开发，，不是一个关于博弈结果的合理预测。

在图6-6中博弈存在三个Nash 均衡——))((开发不开发开发，，、))((不开发不开发开发，，和))((开发开发不开发，，，但这三个均衡是否都是合理的呢？在“新产品开发博弈”中，如果市场需求小，那么就只能一个企业开发，另一个企业不开发。

问题在于谁选择开发，谁选择不开发。

对于先行动的企业1来讲，只要自己选择“开发”，理性的企业2就只会选择“不开发”2，所以均衡))((开发开发不开发，，是不合理的。

而对于企业2来讲，企业1开发自己当然不应开发，如果企业11参见图1-1.2否则，企业2就会亏本，还不如选择“不开发”。

不开发自己显然应该开发，所以均衡))((不开发不开发开发，，也是不合理的。

因此 ，对于图6-6中的扩展式博弈，合理的Nash 均衡是))((开发不开发开发，，。

（讲！）在图6-8中，博弈存在两个Nash 均衡——)),,(()),,((D F B D E B 和。

子博弈精炼纳什均衡●将纳什均衡中包含的不可置信的威胁策略剔除出去。

它要求参与者的决策在任何时点上都是最优的，决策者要“随机应变”，“向前看”，而不是固守旧略。

●由于剔除了不可置信的威胁，在许多情况下，精炼纳什均衡也就缩小了纳什均衡的个数。

这一点对预测分析是非常有意义的。

与纳什均衡的区别●在纳什均衡中，参与人在选择自己战略时，把其他参与人策略当作给定的，不考虑自己的选择将如何影响对手的策略。

●实际上，当一个人行动在前，另一个人行动在后时，后者自然会根据前者的选择而调整自己的选择，前者在作选择时自然会理性地考虑这一点，所以不可能不考虑自己的选择对其对手选择的影响。

博弈表达的标准型与扩展型●博弈的标准型表达有三个要素：参与人，可选择策略及支付函数。

•两人有限策略博弈的标准型可用一个矩阵表来表示。

●扩展型表达包括五个要素：•（1）参与人；（2）每个参与人选择行动的时点；（3）每个参与人在每次行动时可供选择的行动集合；（4）每个参与人在每次行动时有关对手过去行动选择的信息；（5）支付函数。

市场进入阻挠博弈●假设一个企业A是市场上的唯一供给者，面临企业B可能的竞争威胁。

企业A有两种可选策略，即斗争与默许。

斗争表现为采用降低价格使B的收益为0，默许意味着维持高价格。

企业B也有两种策略：进入或者不进入。

假定进入之前垄断利润为300，进入之后寡头利润共为100（各得50），进入成本是10。

各种策略组合下的支付矩阵如下表：举例分析●该博弈显然有两个纳什均衡，即（进入，高价），（不进入，低价）。

●静态分析方法，得到两个纳什均衡。

分析●给定企业B进入的话，企业A选择高价时得50利润，选择低价时得不到利润，所以最优战略是高价（默许）。

同理，给定企业A高价时，进入策略成为企业B最优选择。

尽管在企业B 选择不进入时，企业A采取任何一种策略都是一样得，但只有当企业A选择低价时，不进入才是企业B的最优选择，所以（不进入，低价）也是一个纳什均衡，而（不进入，高价）不是纳什均衡。