理论力学谢传锋第九章习题解答
- 格式:doc
- 大小:1.24 MB
- 文档页数:12
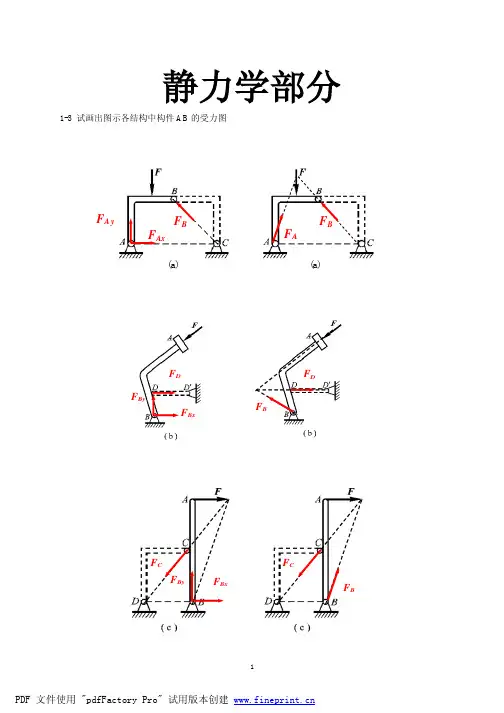

9-1在图示系统中,均质杆OA 、AB 与均质轮的质量均为m ,OA 杆的长度为1l ,AB 杆的长度为2l ,轮的半径为R ,轮沿水平面作纯滚动。
在图示瞬时,OA 杆的角速度为ω,求整个系统的动量。
ω125ml ,方向水平向左题9-1图 题9-2图9-2 如下图,均质圆盘半径为R ,质量为m ,不计质量的细杆长l ,绕轴O 转动,角速度为ω,求以下三种情况下圆盘对固定轴的动量矩: (a )圆盘固结于杆;(b )圆盘绕A 轴转动,相对于杆OA 的角速度为ω-; (c )圆盘绕A 轴转动,相对于杆OA 的角速度为ω。
(a )ω)l R (m L O 222+=;(b )ω2ml L O =;(c )ω)l R (m L O 22+= 9-3水平圆盘可绕铅直轴z 转动,如下图,其对z 轴的转动惯量为z J 。
一质量为m 的质点,在圆盘上作匀速圆周运动,质点的速度为0v ,圆的半径为r ,圆心到盘中心的距离为l 。
开始运动时,质点在位置0M ,圆盘角速度为零。
求圆盘角速度ω与角ϕ间的关系,轴承摩擦不计。
9-4如下图,质量为m 的滑块A ,可以在水平光滑槽中运动,具有刚性系数为k 的弹簧一端与滑块相连接,另一端固定。
杆AB 长度为l ,质量忽略不计,A 端与滑块A 铰接,B 端装有质量1m ,在铅直平面可绕点A 旋转。
设在力偶M 作用下转动角速度ω为常数。
求滑块A 的运动微分方程。
t l m m m x m m kxωωsin 2111+=++9-5质量为m,半径为R的均质圆盘,置于质量为M的平板上,沿平板加一常力F。
设平板与地面间摩擦系数为f,平板与圆盘间的接触是足够粗糙的,求圆盘中心A点的加速度。
9-6均质实心圆柱体A 和薄铁环B 的质量均为m ,半径都等于r ,两者用杆AB 铰接,无滑动地沿斜面滚下,斜面与水平面的夹角为θ,如下图。
如杆的质量忽略不计,求杆AB 的加速度和杆的力。
θsin 74g a =; 9-7均质圆柱体A 和B 的质量均为m ,半径为r ,一绳缠在绕固定轴O 转动的圆柱A 上,绳的另一端绕在圆柱B 上,如下图。
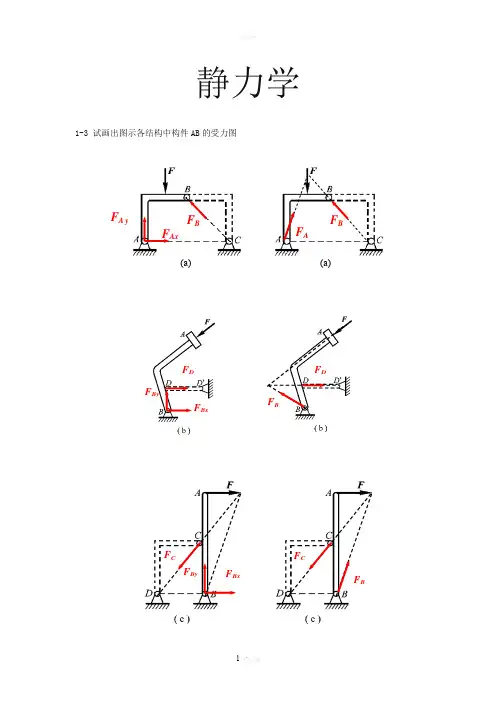
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yFB(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A yF D F ByF A F BxF B F AF Ax F A yF Dy T E F CxF C yN’F BF DF ANF AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
45030对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。


9-10 在瓦特行星传动机构中,平衡杆O 1A 绕O 1轴转动,并借连杆AB 带动曲柄OB ;而曲柄OB 活动地装置在O 轴上,如图所示。
在O 轴上装有齿轮Ⅰ,齿轮Ⅱ与连杆AB 固连于一体。
已知:r 1=r 2=0.33m ,O 1A =0.75m ,AB =1.5m ;又平衡杆的角速度O 1=6rad/s 。
求当=60°且=90°时,曲柄OB 和齿轮Ⅰ的角速度。
题9-10图【知识要点】 Ⅰ、Ⅱ两轮运动相关性。
【解题分析】 本题已知平衡杆的角速度,利用两轮边缘切向线速度相等,找出ωAB ,ωOB 之间的关系,从而得到Ⅰ轮运动的相关参数。
【解答】 A 、B 、M 三点的速度分析如图所示,点C 为AB 杆的瞬心,故有 ABA O CA v A AB ⋅⋅==21ωω ωω⋅=⋅=A O CD v AB B 123所以 s rad r r v BOB /75.321=+=ωs rad r v CM v MAB M /6,1==⋅=I ωω 9-12 图示小型精压机的传动机构,OA =O 1B =r =0.1m ,EB =BD =AD =l =0.4m 。
在图示瞬时,OA ⊥AD ,O 1B ⊥ED ,O 1D 在水平位置,OD 和EF 在铅直位置。
已知曲柄OA 的转速n =120r/min ,求此时压头F 的速度。
题9-12图【知识要点】 速度投影定理。
【解题分析】 由速度投影定理找到A 、D 两点速度的关系。
再由D 、E 、F 三者关系,求F 速度。
【解答】 速度分析如图,杆ED 与AD 均为平面运动,点P 为杆ED 的速度瞬心,故 v F = v E = v D由速度投影定理,有A D v v =⋅θcos可得 s ll r n r v v A F /30.1602cos 22m =+⋅⋅==πθ 9-16 曲柄OA 以恒定的角速度=2rad/s 绕轴O 转动,并借助连杆AB 驱动半径为r 的轮子在半径为R 的圆弧槽中作无滑动的滚动。
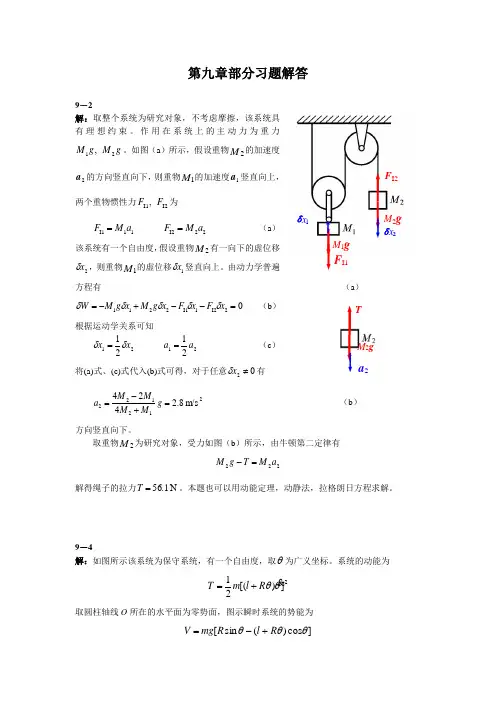
第九章部分习题解答9-2解:取整个系统为研究对象,不考虑摩擦,该系统具有理想约束。
作用在系统上的主动力为重力g M g M 21,。
如图(a )所示,假设重物2M 的加速度2a 的方向竖直向下,则重物1M 的加速度1a 竖直向上,两个重物惯性力I2I1,F F 为11I1a M F = 22I2a M F =(a )该系统有一个自由度,假设重物2M 有一向下的虚位移2x δ,则重物1M 的虚位移1x δ竖直向上。
由动力学普遍方程有 (a )02I21I12211=--+-=x F x F x g M x g M W δδδδδ (b )根据运动学关系可知2121x x δδ=2121a a =(c )将(a)式、(c)式代入(b)式可得,对于任意02≠x δ有212122m/s 8.2424=+-=g M M M M a (b )方向竖直向下。
取重物2M 为研究对象,受力如图(b )所示,由牛顿第二定律有222a M T g M =-解得绳子的拉力N 1.56=T 。
本题也可以用动能定理,动静法,拉格朗日方程求解。
9-4解:如图所示该系统为保守系统,有一个自由度,取θ为广义坐标。
系统的动能为2])[(21θθ R l m T +=取圆柱轴线O 所在的水平面为零势面,图示瞬时系统的势能为]cos )(sin [θθθR l R mg V +-=M 1gM 2gF I2F I1δx 2δx 1M 2gT a 2拉格朗日函数V T L -=,代入拉格朗日方程0)(=∂∂-∂∂θθL L dt d 整理得摆的运动微分方程为0sin )(2=+++θθθθg R R l 。
9-6解:如图所示,该系统为保守系统,有一个自由度,取弧坐标s 为广义坐标。
系统的动能为221S m T =取轨线最低点O 所在的水平面为零势面,图示瞬时系统的势能为mgh V =由题可知b s ds dh 4sin ==ϕ,因此有b s d b s h So8s 42==⎰。

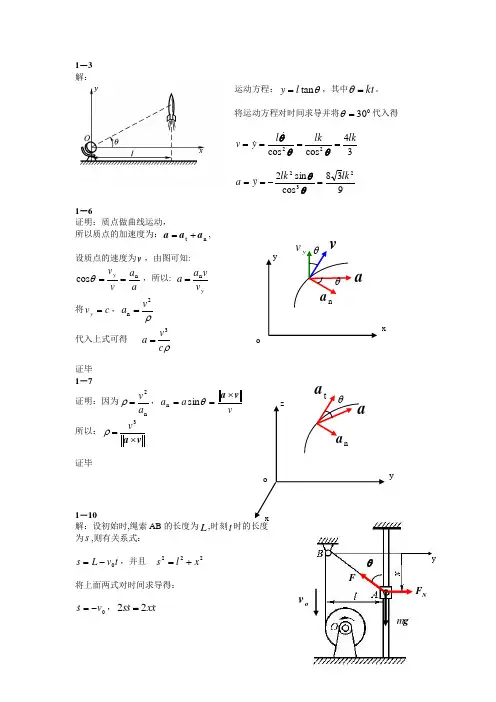
1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将030=θ代入得34cos cos 22lk lk l y v ====θθθ938cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动,所以质点的加速度为:n t a a a +=,设质点的速度为v ,由图可知:a a v v yn cos ==θ,所以: yv va a n =将c v y =,ρ2n va =代入上式可得 ρc v a 3=证毕 1-7证明:因为n2a v =ρ,v a a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10 解:设初始时,绳索AB 的长度为L ,时刻t 时的长度为s ,则有关系式:t v L s 0-=,并且 222x l s +=将上面两式对时间求导得:0v s-= ,x x s s 22= xyoan avy vθθtayzoan aθxovovF N Fg myθ由此解得:xsv x 0-= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得:2002v v s x x x=-=+ (b)将(a)式代入(b)式可得:3220220xlv x x v x a x -=-== (负号说明滑块A 的加速度向上)取套筒A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:g F F a m m N ++=将该式在y x ,轴上投影可得直角坐标形式的运动微分方程:N F F ym F mg xm +-=-=θθsin cos其中:2222sin ,cos l x l lx x +=+=θθ0,3220=-=yx l v x将其代入直角坐标形式的运动微分方程可得:23220)(1)(x lxl v g m F ++=1-11解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即:θcos A B v v = (a ) 因为x R x 22cos -=θ (b )将上式代入(a )式得到A 点速度的大小为:22R x xRv A -=ω (c )由于x v A -=,(c )式可写成:Rx R x x ω=--22 ,将该式两边平方可得:222222)(x R R x xω=-将上式两边对时间求导可得:x x R x x R x xx 2232222)(2ω=--将上式消去x 2后,可求得:22242)(R x xR x--=ω (d)由上式可知滑块A 的加速度方向向左,其大小为 22242)(R x xR a A -=ω取套筒A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:g F F a m m N ++=将该式在y x ,轴上投影可得直角坐标形式的 运动微分方程:mg F F ym F xm N -+=-=θθsin cos其中:x R x xR22cos ,sin -==θθ, 0,)(22242=--=y R x x R x ω将其代入直角坐标形式的运动微分方程可得2525)(,)(225222242R x x R m mg F R x x R m F N --=-=ωω1-13解:动点:套筒A ;动系:OC 杆;定系:机座;xθ AvAω ONF BRg mFyavevr v运动分析:绝对运动:直线运动;相对运动:直线运动;牵连运动:定轴转动。

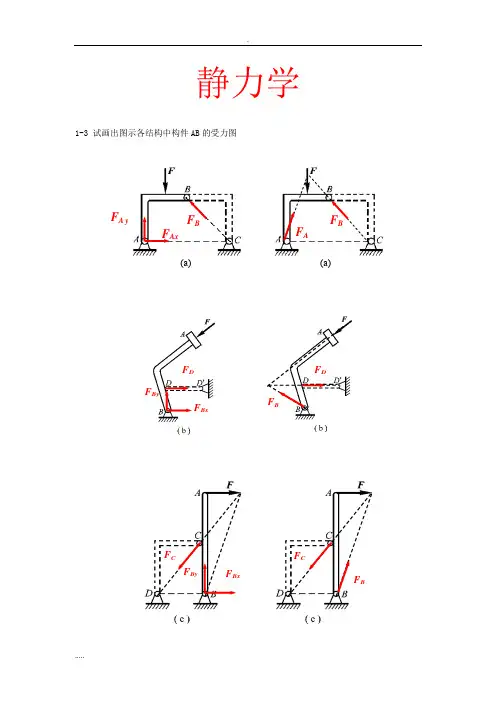
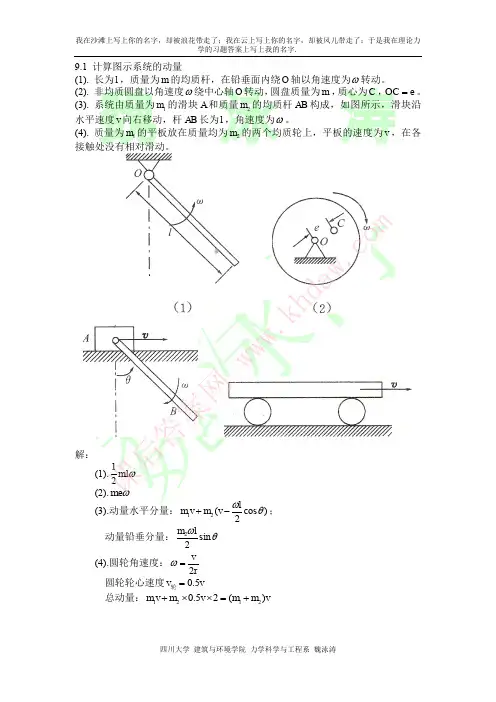
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A yF D F ByF A F BxF B F AF Ax F A yF DyT E F CxF C yN’F BF DF ANF AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
45030对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
9-1.塔式起重机的水平悬臂以匀角速度ω=0.1rad/s 绕铅垂轴OO 1转动,同时跑车A 带着重物B 沿悬臂按x=20-0.5t 的规律运动,单位为米、秒,且悬挂钢索AB 始终保持铅垂。
求当t=10s 时重物B 的绝对速度。
解:动 点:A ;动 系:起重机运动分析:牵连运动:定轴转动; 相对运动:直线运动; 绝对运动:曲线运动;ee r ωx v sm 50dtdx v =-==/.当t=10s 时sm 58151)50(v v v s m 5110)105020(v 222r 2e a e /.../...=+-=+==⨯⨯-=9-2.图示曲柄滑道机构中,曲柄长OA=r ,它以匀角速度ω绕O 轴转动。
装在水平上的滑槽DE 与水平线成60o 角。
求当曲柄与水平线的交角分别为ϕ=0、30o 、60o 时,杆BC 的速度。
解:动 点:A ;动 系:ABC 运动分析:牵连运动:平动; 相对运动:直线运动; 绝对运动:圆周运动;OBC v rv a由正弦定理得:()()()12030φv v φ90v 30φv 120v ae rea sin sin sin sin sin -=-=-=当ϕ=0o 时, ωr 33v e -=当ϕ=30o 时, 0v e = 当ϕ=60o 时, ωr 33v e =9-3.图示曲柄滑道机构中,杆BC 为水平,而杆DE 保持铅垂。
曲柄长OA=10cm ,以匀角速度ω=20rad/s 绕O 轴转动,通过滑块A 使杆BC 作往复运动。
求当曲柄与水平线的交角分别为ϕ=0、30o 、90o 时,杆BC 的速度。
解:动 点:A ;动 系:BDC 运动分析:牵连运动:平动;相对运动:直线运动; 绝对运动:圆周运动;φv v s cm 200ωr v a e a sin /===当ϕ=0o 时, 0v e =;当ϕ=30o 时, s cm 100v e /=; 当ϕ=90o 时, s cm 200v e /=9-4.矿砂从传送带A 落到另一传送带B 的绝对速度为v 1=4m/s ,其方向与铅垂线成30o 角。
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF BF DF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F DF ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF BxF B yF CxF C yF DxF DyF Bx F ByT EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =F ABF BC F CD 60o F 130o F 2 F BC45o F 2F BC F ABB45oy xF CD C60o F 130o F BC x y450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
第九章部分习题解答9-2解:取整个系统为研究对象,不考虑摩擦,该系统具有理想约束。
作用在系统上的主动力为重力g M g M 21,。
如图(a )所示,假设重物2M 的加速度2a 的方向竖直向下,则重物1M 的加速度1a 竖直向上,两个重物惯性力I2I1,F F 为11I1a M F = 22I2a M F =(a )该系统有一个自由度,假设重物2M 有一向下的虚位移2x δ,则重物1M 的虚位移1x δ竖直向上。
由动力学普遍方程有 (a )02I21I12211=--+-=x F x F x g M x g M W δδδδδ (b )根据运动学关系可知2121x x δδ=2121a a =(c )将(a)式、(c)式代入(b)式可得,对于任意02≠x δ有212122m/s 8.2424=+-=g M M M M a (b )方向竖直向下。
取重物2M 为研究对象,受力如图(b )所示,由牛顿第二定律有222a M T g M =-解得绳子的拉力N 1.56=T 。
本题也可以用动能定理,动静法,拉格朗日方程求解。
9-4解:如图所示该系统为保守系统,有一个自由度,取θ为广义坐标。
系统的动能为2])[(21θθ R l m T +=取圆柱轴线O 所在的水平面为零势面,图示瞬时系统的势能为]cos )(sin [θθθR l R mg V +-=M 1gM 2gF I2F I1δx 2δx 1M 2gTa 2拉格朗日函数V T L -=,代入拉格朗日方程0)(=∂∂-∂∂θθL L dt d 整理得摆的运动微分方程为0sin )(2=+++θθθθg R R l 。
9-6解:如图所示,该系统为保守系统,有一个自由度,取弧坐标s 为广义坐标。
系统的动能为221S m T =取轨线最低点O 所在的水平面为零势面,图示瞬时系统的势能为mgh V =由题可知b sds dh 4sin ==ϕ,因此有b s d b s h So8s 42==⎰。
则拉格朗日函数 22821s bmg s m V T L -=-= 代入拉格朗日方程0)(=∂∂-∂∂s L s L dt d ,整理得摆的运动微分方程为04=+s bgs 。
解得质点的运动规律为)21sin(0ϕ+=t bgA s ,其中0,ϕA 为积分常数。
9-13解:1.求质点的运动微分方程圆环(质量不计)以匀角速度ω绕铅垂轴AB 转动,该系统有一个自由度,取角度θ为广义坐标。
系统的动能为22)sin (21)(21θωθr m r m T += 如图所示,取0=θ为零势位,图示瞬时系统的势能为零势面h)cos 1(θ-=mgr V则拉格朗日函数)cos 1()sin (212222θθωθ--+=-=mgr mr V T L 代入拉格朗日方程0)(=∂∂-∂∂θθL L dt d ,整理得质点的运动微分方程为0sin )cos (2=-+θθωθrg 2.求维持圆环作匀速转动的力偶M如果求力偶M ,必须考虑圆环绕铅垂轴AB 的一般转动。
因此解除“圆环绕铅垂轴AB 匀速ω转动”这一约束,将力偶M 视为主动力。
此时系统有两个自由度,取角度θ和圆环绕轴AB 的转角ϕ为广义坐标,系统的势能不变,动能表达式中以ϕ代替ω,则拉格朗日函数为)cos 1()sin (212222θθϕθ--+=-=mgr mr V T L 力偶M 为非有势力,它对应于广义坐标θ和ϕ的广义力计算如下:取0,0=≠δϕδθ,在这组虚位移下力偶M 所做的虚功为0][=δθδW ,因此力偶M 对应于广义坐标θ的广义力0=MQ θ;取0,0≠=δϕδθ,在这组虚位移下力偶M 所做的虚功为δϕδδϕ⋅=M W ][,因此力偶M 对应于广义坐标ϕ的广义力M W Q M==δϕδδϕϕ][。
代入拉格朗日方程0)(==∂∂-∂∂M Q L L dt d θθθ ,整理可得 0sin =+θθrg 代入拉格朗日方程M Q L L dt d M==∂∂-∂∂ϕϕϕ)( ,整理可得 M mr mr =+θϕθϕθ 2sin sin 222 圆环绕铅垂轴AB 以匀速ω转动,即0,==ϕωϕ,代入上式可得θθω2sin 2mr M =。
零势位9-14解: 以刚体为研究对象,有一个自由度。
如图(a )所示,取G O 3和OC 的夹角θ为广义坐标。
若以框架OC O O 21为动系,则刚体的相对运动是以角速度θ 绕轴21O O 的定轴转动,牵连运动是以角速度ω绕OC 轴的定轴转动,绝对角速度a ω是θ 和ω的矢量和。
以21O O 为x '轴,G O 3为y '轴,建立一个固连在刚体上的坐标系,该刚体的角速度a ω可表示成a ωz j i '-'+'=θωθωsin cos θ(a ) (b )由于坐标系z y x O '''3的三个坐标轴为过3O 点的三个惯量主轴,则系统的动能为])sin ()cos ([21232221θωθωθJ J J T ++= 取0=θ为零势位,图示瞬时系统的势能为)cos 1(θ-=mgl V ,则拉格朗日函数)cos 1(])sin ()cos ([21232221θθωθωθ--++=-=mgl J J J V T L 代入拉格朗日方程0)(=∂∂-∂∂θθL L dt d ,整理可得物体的运动微分方程为 θθθωθsin cos sin )(3221mgl J J J -=-+9-15x ’ z ’y ’ωθzGωO 3θ 垂直于O 1O 2的平面y ’解:框架(质量不计)以匀角速度ω绕铅垂边转动,系统有一个自由度,取AB 杆与铅垂边的夹角θ为广义坐标。
若以框架为动系,AB 杆上任意一点的速度是该点相对于框架的相对速度和随框架运动的牵连速度的矢量和,且相对速度和牵连速度相互垂直, 因此杆AB 的动能可表示为相对于框架运动的动能和随框架转动的动能之和。
如图所示,AB 杆相对于框架作平面运动,“速度瞬心”为O 点,设AB 杆的质心为C ,由几何关系可知l BC OC AC ===,则质心为C 的速度大小为θl v C =。
杆AB 相对于框架运动的动能 22222C 132])2(121[2121θθml l m mv T =+= 杆AB 随框架转动的动能θωθω2222022sin 32)sin (221ml x dx l m T l ==⎰ 系统的动能21T T T +=。
假设090=θ时杆势能为零,则任意位置系统的势能为θcos mgl V =。
则拉格朗日函数θθωθcos )sin (322222mgl ml V T L -+=-= 代入拉格朗日方程0)(=∂∂-∂∂θθL L dt d ,整理得系统的运动微分方程 0sin 3cos sin 442=--θθθωθg l l 由于角θ描述的是杆AB 相对于框架的位置变化,因此上式也就是杆的相对运动微分方程。
9-17解:取楔块A ,B 构成的系统为研究对象,该系统有二个自由度,取楔块A 水平滑动的位移x ,以及楔块B 相对于A 滑动的位移s 为广义坐标。
若以楔块A 为动系,则楔块A 的速度A v ,楔块B 的速度B v ,以及B 相对于A 的相对速度满足如下的矢量关系(方向如图所示)Br A B v v v +=系统的动能为CO xsA vBrv])sin ()cos [(222121222212B B 2A A ϕϕs s x g P xg P v m v m T +++=+= 22222121cos 1)(21s P gs x P g x P P g +++=ϕ 取过x 轴的水平为零势面,某瞬时系统的势能为ϕsin 2s P V =。
则拉格朗日函数ϕϕsin 21cos 1)(212222221s P s P gs x P g x P P g V T L -+++=-= 水平力F 对应于广义坐标x 和s 的广义力计算如下:取0,0=≠s x δδ,在这组虚位移下力F 所做的虚功为x F W x δδδ=][,因此力F 对应于广义坐标x 的广义力F Q Fx =;取0,0≠=s x δδ,在这组虚位移下力F 所做的虚功为s F W s ϕδδδcos ][=,因此力F 对应于广义坐标s 的广义力ϕcos F Q Fs =。
代入拉格朗日方程F Q xL x L dt d F x ==∂∂-∂∂)( ,整理可得 Fg sP x P P =++ ϕcos )(221(a )代入拉格朗日方程ϕcos )(F Q sL s L dt d F s ==∂∂-∂∂ ,整理可得 g P F sP x P )sin cos (cos 222ϕϕϕ-=+(b )由方程(a )、(b )解得 楔块A 的加速度:ϕϕϕϕsin sin cos sin 2212A g P P P F xa ++== ,方向水平向右。
楔块B 的相对加速度:g P P P P P P FP s a )sin (sin )(cos 22122211Br ϕϕϕ++-==,方向沿斜面向上。
9-18解:取楔块ABC 和圆柱构成的系统为研究对象,该系统为保守系统,有二个自由度,取楔块水平滑动的位移x ,以及圆柱的转角ϕ(A 点ϕ=0)为广义坐标。
若以楔块为动系,则楔块的速度A v ,圆柱轴心O 的速度o v ,以及轴心O 相对A 的相对速度满足如下的矢量关系(方向如图所示)Or A O v v v +=圆柱在斜面上作纯滚动有:r v ϕ=Or 。
系统的动能为2212O 12A )21(212121ϕr m v m mv T ++= 221221241])sin ()cos [(2121ϕθϕθϕ r m r r x m xm ++-+=22112143cos )(21ϕϕθ r m x r m xm m +-+= 取过楔块上A 点的水平面为零势面,图示瞬时系统的势能为θϕsin 1r g m V -=则拉格朗日函数θϕϕϕθsin 43cos )(211221121r g m r m x r m xm m V T L ++-+=-= 代入拉格朗日方程0)(=∂∂-∂∂xL x L dt d ,整理可得 0cos )(11=⋅-+ϕθ r m xm m(a )代入拉格朗日方程0)(=∂∂-∂∂ϕϕL L dt d ,整理可得 θθϕsin 2cos 23g xr =- (b )求解方程(a )、(b )得楔块的加速度: g m m m m x a θθ2111cos 2)(32sin -+==,方向水平向左。
圆柱的角加速度:g rm m m m m ]cos 2)(3[sin )(22111θθϕα-++== ,顺时针方向。