理论力学课后答案9

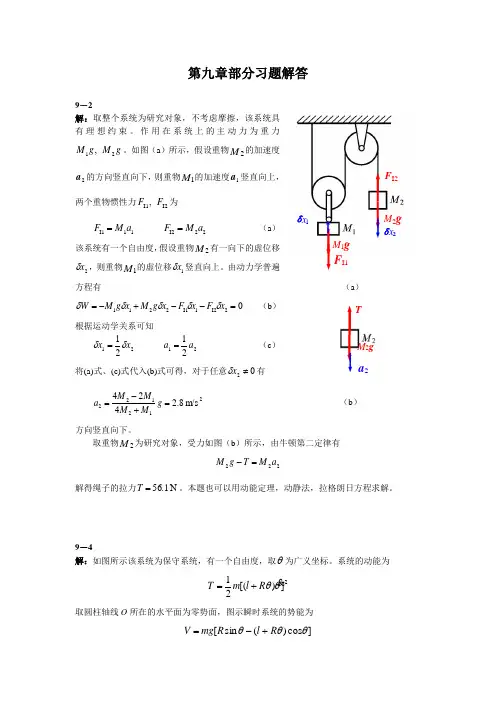
第九章部分习题解答9－2解：取整个系统为研究对象，不考虑摩擦，该系统具有理想约束。

作用在系统上的主动力为重力g M g M 21,。

如图（a ）所示，假设重物2M 的加速度2a 的方向竖直向下，则重物1M 的加速度1a 竖直向上，两个重物惯性力I2I1,F F 为11I1a M F = 22I2a M F =（a ）该系统有一个自由度，假设重物2M 有一向下的虚位移2x δ，则重物1M 的虚位移1x δ竖直向上。

由动力学普遍方程有 （a ）02I21I12211=--+-=x F x F x g M x g M W δδδδδ （b ）根据运动学关系可知2121x x δδ=2121a a =（c ）将(a)式、(c)式代入(b)式可得，对于任意02≠x δ有212122m/s 8.2424=+-=g M M M M a （b ）方向竖直向下。

取重物2M 为研究对象，受力如图（b ）所示，由牛顿第二定律有222a M T g M =-解得绳子的拉力N 1.56=T 。

本题也可以用动能定理，动静法，拉格朗日方程求解。

9－4解：如图所示该系统为保守系统，有一个自由度，取θ为广义坐标。

系统的动能为2])[(21θθ R l m T +=取圆柱轴线O 所在的水平面为零势面，图示瞬时系统的势能为]cos )(sin [θθθR l R mg V +-=M 1gM 2gF I2F I1δx 2δx 1M 2gT a 2拉格朗日函数V T L -=，代入拉格朗日方程0)(=∂∂-∂∂θθL L dt d 整理得摆的运动微分方程为0sin )(2=+++θθθθg R R l 。

9－6解：如图所示，该系统为保守系统，有一个自由度，取弧坐标s 为广义坐标。

系统的动能为221S m T =取轨线最低点O 所在的水平面为零势面，图示瞬时系统的势能为mgh V =由题可知b s ds dh 4sin ==ϕ，因此有b s d b s h So8s 42==⎰。

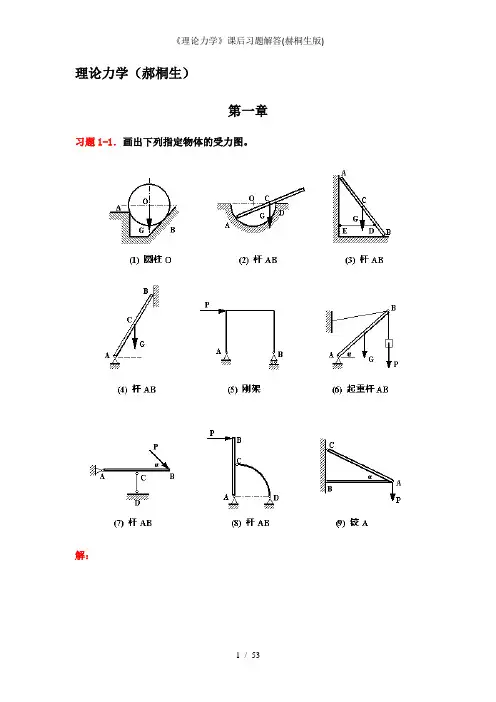
理论力学（郝桐生）第一章习题1-1．画出下列指定物体的受力图。

解：习题1-2．画出下列各物系中指定物体的受力图。

解：习题1-3．画出下列各物系中指定物体的受力图。

解：第二章习题2-1．铆接薄钢板在孔心A、B和C处受三力作用如图，已知P1=100N沿铅垂方向，P2=50N沿AB方向，P3=50N沿水平方向；求该力系的合成结果。

解：属平面汇交力系；合力大小和方向：习题2-2．图示简支梁受集中荷载P=20kN，求图示两种情况下支座A、B的约束反力。

解：(1)研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：(2) 研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：习题2-3．电机重P=5kN放在水平梁AB的中央，梁的A端以铰链固定，B端以撑杆BC支持。

求撑杆BC所受的力。

解：(1)研究整体，受力分析：(2) 画力三角形：(3) 求BC受力习题2-4．简易起重机用钢丝绳吊起重量G=2kN的重物，不计杆件自重、磨擦及滑轮大小，A、B、C三处简化为铰链连接；求杆AB和AC所受的力。

解：(1) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆受拉，BC杆受压。

(2) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆实际受力方向与假设相反，为受压；BC杆受压。

习题2-5．三铰门式刚架受集中荷载P作用，不计架重；求图示两种情况下支座A、B的约束反力。

解：(1) 研究整体，受力分析（AC是二力杆）；画力三角形：求约束反力：(2) 研究整体，受力分析（BC是二力杆）；画力三角形：几何关系：求约束反力：习题2-6．四根绳索AC、CB、CE、ED连接如图，其中B、D两端固定在支架上，A端系在重物上，人在E点向下施力P，若P=400N，α=4o，求所能吊起的重量G。

解：(1) 研究铰E，受力分析，画力三角形：由图知：(2) 研究铰C，受力分析，画力三角形：由图知：习题2-7．夹具中所用的两种连杆增力机构如图所示，书籍推力P作用于A点，夹紧平衡时杆AB与水平线的夹角为；求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。

9-10在瓦特行星传动机构中，平衡杆O1A 绕O1 轴转动，并借连杆AB 带动曲柄OB；而曲柄OB 活动地装置在O 轴上，如图所示。

在O 轴上装有齿轮Ⅰ，齿轮Ⅱ与连杆AB 固连于一体。

已知：r1＝r2＝0.3 3m，O1A＝0.75m，AB＝1.5m；又平衡杆的角速度O1＝6rad/s。

求当＝60°且＝90°时，曲柄OB 和齿轮Ⅰ的角速度。

题9－10 图【知识要点】Ⅰ、Ⅱ两轮运动相关性。

【解题分析】本题已知平衡杆的角速度，利用两轮边缘切向线速度相等，找出ωAB ,ωOB 之间的关系，从而得到Ⅰ轮运动的相关参数。

【解答】A、B、M 三点的速度分析如图所示，点 C 为AB 杆的瞬心，故有v A O1 AB 2CA A AB3v B CD AB O12Av B所以OB 3 .75rad / sr r1 2vMv M CM , 6rad /ABr1s9-12图示小型精压机的传动机构，OA＝O1B＝r＝0.1m，EB＝BD＝AD＝l＝0.4m。

在图示瞬时，OA⊥AD，O1B⊥ED，O1D 在水平位置，OD 和EF 在铅直位置。

已知曲柄OA 的转速n＝120r/min ，求此时压头 F 的速度。

题9－12 图【知识要点】速度投影定理。

【解题分析】由速度投影定理找到 A 、D 两点速度的关系。

再由D、E、F 三者关系，求 F 速度。

【解答】速度分析如图，杆ED 与AD 均为平面运动，点P为杆ED 的速度瞬心，故v F = v E = v D由速度投影定理，有v D cos vA2 2v r 2n r lA可得v F 1.30 / smcos 60 l9-16 曲柄OA 以恒定的角速度＝2rad/s 绕轴O 转动，并借助连杆AB 驱动半径为r 的轮子在半径为R 的圆弧槽中作无滑动的滚动。

设OA＝AB＝R＝2r＝1m，求图示瞬时点 B 和点 C 的速度与加速度。

题9－16 图【知识要点】基点法求速度和加速度。

理论力学第七版课后习题答案第一章: 引言习题1-11.问题描述：给定物体的质量m=2kg，加速度a=3m/s^2，求引力F。

2.解答：根据牛顿第二定律F=ma，其中m表示物体的质量，a表示物体的加速度。

代入已知值，可求得F=6N。

习题1-21.问题描述：给定物体的质量m=5kg，引力F=20N，求加速度a。

2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=4m/s^2。

第二章: 运动的描述习题2-11.问题描述：一个物体以恒定速度v=10m/s匀速直线运动，经过t=5s，求物体的位移。

2.解答：位移等于速度乘以时间，即s=vt。

代入已知值，可得s=50m。

习题2-21.问题描述：一个物体以初始速度v0=5m/s匀加速直线运动，加速度a=2m/s^2，经过t=3s，求物体的位移。

2.解答：由于物体是匀加速直线运动，位移可以通过公式s=v0t+0.5at^2计算。

代入已知值，可得s=(53)+(0.52*3^2)=45m。

第三章: 动力学基础习题3-11.问题描述：一个物体质量为m=4kg，受到的力F=10N，求物体的加速度。

2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2.5m/s^2。

习题3-21.问题描述：一个物体质量为m=3kg，受到的力F=6N，求物体的加速度。

2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2m/s^2。

第四章: 动力学基本定理习题4-11.问题描述：一个物体质量为m=8kg，受到的力F=16N，求物体的加速度。

2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2m/s^2。

习题4-21.问题描述：一个物体质量为m=6kg，受到的力F=12N，求物体的加速度。

2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2m/s^2。

以上是理论力学第七版课后习题的答案。

希望能对你的学习有所帮助！。

理论力学（郝桐生）第一章习题1-1．画出下列指定物体的受力图。

解：习题1-2．画出下列各物系中指定物体的受力图。

解：习题1-3．画出下列各物系中指定物体的受力图。

解：第二章习题2-1．铆接薄钢板在孔心A、B和C处受三力作用如图，已知P1=100N沿铅垂方向，P2=50N沿AB方向，P3=50N沿水平方向；求该力系的合成结果。

解：属平面汇交力系；合力大小和方向：习题2-2．图示简支梁受集中荷载P=20kN，求图示两种情况下支座A、B的约束反力。

解：(1)研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：(2) 研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：习题2-3．电机重P=5kN放在水平梁AB的中央，梁的A端以铰链固定，B端以撑杆BC支持。

求撑杆BC所受的力。

解：(1)研究整体，受力分析：(2) 画力三角形：(3) 求BC受力习题2-4．简易起重机用钢丝绳吊起重量G=2kN的重物，不计杆件自重、磨擦及滑轮大小，A、B、C三处简化为铰链连接；求杆AB和AC所受的力。

解：(1) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆受拉，BC杆受压。

(2) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆实际受力方向与假设相反，为受压；BC杆受压。

习题2-5．三铰门式刚架受集中荷载P作用，不计架重；求图示两种情况下支座A、B的约束反力。

解：(1) 研究整体，受力分析（AC是二力杆）；画力三角形：求约束反力：(2) 研究整体，受力分析（BC是二力杆）；画力三角形：几何关系：求约束反力：习题2-6．四根绳索AC、CB、CE、ED连接如图，其中B、D两端固定在支架上，A端系在重物上，人在E点向下施力P，若P=400N，α=4o，求所能吊起的重量G。

解：(1) 研究铰E，受力分析，画力三角形：由图知：(2) 研究铰C，受力分析，画力三角形：由图知：习题2-7．夹具中所用的两种连杆增力机构如图所示，书籍推力P作用于A点，夹紧平衡时杆AB与水平线的夹角为；求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。

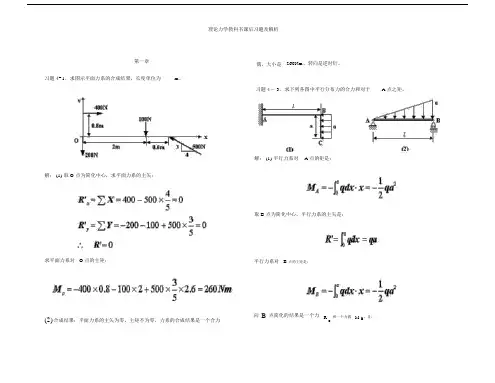
理论力学教科书课后习题及解析第一章偶，大小是260Nm，转向是逆时针。

习题 4- 1．求图示平面力系的合成结果，长度单位为m。

习题 4－ 3．求下列各图中平行分布力的合力和对于 A 点之矩。

解： (1) 平行力系对 A 点的矩是：解： (1) 取 O 点为简化中心，求平面力系的主矢：取 B 点为简化中心，平行力系的主矢是：求平面力系对O 点的主矩：平行力系对 B 点的主矩是：(2)合成结果：平面力系的主矢为零，主矩不为零，力系的合成结果是一个合力向B点简化的结果是一个力RB和一个力偶M B，且：如图所示；向 A 点简化的结果是一个力R A和一个力偶M A，且：如图所示；将 R B向下平移一段距离d，使满足：最后简化为一个力R ，大小等于R B。

其几何意义是： R 的大小等于载荷分布的将 R A向右平移一段距离d，使满足：矩形面积，作用点通过矩形的形心。

(2)取 A 点为简化中心，平行力系的主矢是：最后简化为一个力R，大小等于R A。

其几何意义是：R 的大小等于载荷分布的三角形面积，作用点通过三角形的形心。

平行力系对 A 点的主矩是：列平衡方程：习题 4-4 ．求下列各梁和刚架的支座反力，长度单位为m。

解方程组：反力的实际方向如图示。

校核：解： (1) 研究 AB 杆，受力分析，画受力图：结果正确。

(2) 研究 AB 杆，受力分析，将线性分布的载荷简化成一个集中力，画受力图：(3) 研究 ABC ，受力分析，将均布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：列平衡方程：反力的实际方向如图示。

校核：解方程组：结果正确。

反力的实际方向如图示。

校核：结果正确。

习题 4-5 ．重物悬挂如图，已知G=1.8kN ，其他重量不计；求铰链 A 的约束反力和杆 BC 所受的力。

列平衡方程：解方程组：解： (1) 研究整体，受力分析（BC 是二力杆），画受力图：反力的实际方向如图示。

列平衡方程：习题 4-8 ．图示钻井架，G=177kN ，铅垂荷载P=1350kN ，风荷载 q=1.5kN/m ，水平力 F=50kN ；求支座 A 的约束反力和撑杆CD 所受的力。

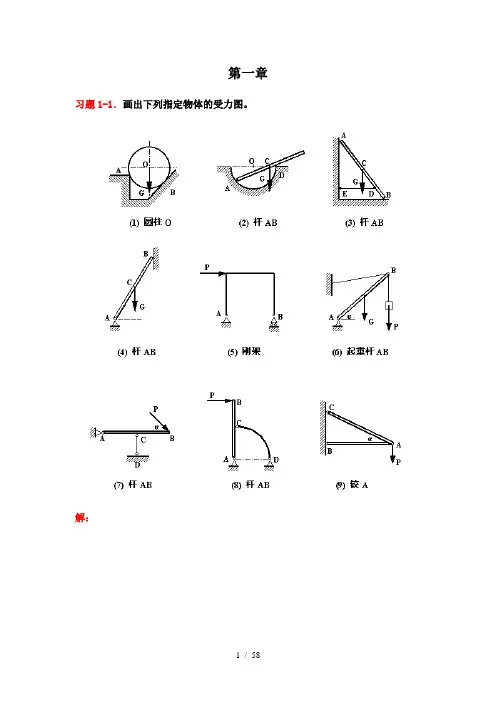
第一章习题1-1．画出下列指定物体的受力图。

解：习题1-2．画出下列各物系中指定物体的受力图。

解：习题1-3．画出下列各物系中指定物体的受力图。

解：第二章习题2-1．铆接薄钢板在孔心A、B和C处受三力作用如图，已知P1=100N沿铅垂方向，P2=50N沿AB方向，P3=50N沿水平方向；求该力系的合成结果。

解：属平面汇交力系；合力大小和方向：习题2-2．图示简支梁受集中荷载P=20kN，求图示两种情况下支座A、B的约束反力。

解：(1)研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：(2) 研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：习题2-3．电机重P=5kN放在水平梁AB的中央，梁的A端以铰链固定，B端以撑杆BC支持。

求撑杆BC所受的力。

解：(1)研究整体，受力分析：(2) 画力三角形：(3) 求BC受力习题2-4．简易起重机用钢丝绳吊起重量G=2kN的重物，不计杆件自重、磨擦及滑轮大小，A、B、C三处简化为铰链连接；求杆AB和AC所受的力。

解：(1) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆受拉，BC杆受压。

(2) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆实际受力方向与假设相反，为受压；BC杆受压。

习题2-5．三铰门式刚架受集中荷载P作用，不计架重；求图示两种情况下支座A、B的约束反力。

解：(1) 研究整体，受力分析（AC是二力杆）；画力三角形：求约束反力：(2) 研究整体，受力分析（BC是二力杆）；画力三角形：几何关系：求约束反力：习题2-6．四根绳索AC、CB、CE、ED连接如图，其中B、D两端固定在支架上，A端系在重物上，人在E点向下施力P，若P=400N，α=4o，求所能吊起的重量G。

解：(1) 研究铰E，受力分析，画力三角形：由图知：(2) 研究铰C，受力分析，画力三角形：由图知：习题2-7．夹具中所用的两种连杆增力机构如图所示，书籍推力P作用于A点，夹紧平衡时杆AB与水平线的夹角为；求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。

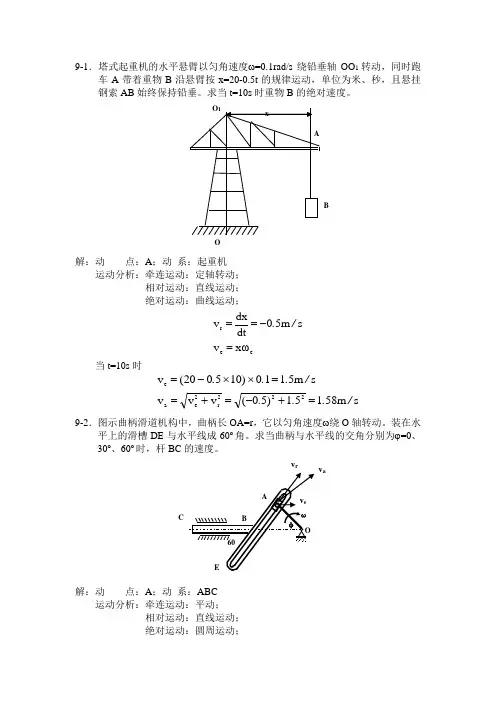
9-1．塔式起重机的水平悬臂以匀角速度ω=0.1rad/s 绕铅垂轴OO 1转动，同时跑车A 带着重物B 沿悬臂按x=20-0.5t 的规律运动，单位为米、秒，且悬挂钢索AB 始终保持铅垂。

求当t=10s 时重物B 的绝对速度。

解：动 点：A ；动 系：起重机运动分析：牵连运动：定轴转动； 相对运动：直线运动； 绝对运动：曲线运动；ee r ωx v sm 50dtdx v =-==/.当t=10s 时sm 58151)50(v v v s m 5110)105020(v 222r 2e a e /.../...=+-=+==⨯⨯-=9-2．图示曲柄滑道机构中，曲柄长OA=r ，它以匀角速度ω绕O 轴转动。

装在水平上的滑槽DE 与水平线成60o 角。

求当曲柄与水平线的交角分别为ϕ=0、30o 、60o 时，杆BC 的速度。

解：动 点：A ；动 系：ABC 运动分析：牵连运动：平动； 相对运动：直线运动； 绝对运动：圆周运动；OBC v rv a由正弦定理得：()()()12030φv v φ90v 30φv 120v ae rea sin sin sin sin sin -=-=-=当ϕ=0o 时， ωr 33v e -=当ϕ=30o 时， 0v e = 当ϕ=60o 时， ωr 33v e =9-3．图示曲柄滑道机构中，杆BC 为水平，而杆DE 保持铅垂。

曲柄长OA=10cm ，以匀角速度ω=20rad/s 绕O 轴转动，通过滑块A 使杆BC 作往复运动。

求当曲柄与水平线的交角分别为ϕ=0、30o 、90o 时，杆BC 的速度。

解：动 点：A ；动 系：BDC 运动分析：牵连运动：平动；相对运动：直线运动； 绝对运动：圆周运动；φv v s cm 200ωr v a e a sin /===当ϕ=0o 时， 0v e =；当ϕ=30o 时， s cm 100v e /=； 当ϕ=90o 时， s cm 200v e /=9-4．矿砂从传送带A 落到另一传送带B 的绝对速度为v 1=4m/s ，其方向与铅垂线成30o 角。

第一章习题4-1．求图示平面力系的合成结果，长度单位为m。

解：(1) 取O点为简化中心，求平面力系的主矢：求平面力系对O点的主矩：(2) 合成结果：平面力系的主矢为零，主矩不为零，力系的合成结果是一个合力偶，大小是260Nm，转向是逆时针。

习题4－3．求下列各图中平行分布力的合力和对于A点之矩。

解：(1) 平行力系对A点的矩是：取B点为简化中心，平行力系的主矢是：平行力系对B点的主矩是：向B点简化的结果是一个力R B和一个力偶M B，且：如图所示；将R B向下平移一段距离d，使满足：最后简化为一个力R，大小等于R B。

其几何意义是：R的大小等于载荷分布的矩形面积，作用点通过矩形的形心。

(2) 取A点为简化中心，平行力系的主矢是：平行力系对A点的主矩是：向A点简化的结果是一个力R A和一个力偶M A，且：如图所示；将R A向右平移一段距离d，使满足：最后简化为一个力R，大小等于R A。

其几何意义是：R的大小等于载荷分布的三角形面积，作用点通过三角形的形心。

习题4-4．求下列各梁和刚架的支座反力，长度单位为m。

解：(1) 研究AB杆，受力分析，画受力图：列平衡方程：解方程组：反力的实际方向如图示。

校核：结果正确。

(2) 研究AB杆，受力分析，将线性分布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。

校核：结果正确。

(3) 研究ABC，受力分析，将均布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。

校核：结果正确。

习题4-5．重物悬挂如图，已知G=1.8kN，其他重量不计；求铰链A的约束反力和杆BC所受的力。

解：(1) 研究整体，受力分析（BC是二力杆），画受力图：列平衡方程：解方程组：反力的实际方向如图示。

习题4-8．图示钻井架，G=177kN，铅垂荷载P=1350kN，风荷载q=1.5kN/m，水平力F=50kN；求支座A的约束反力和撑杆CD所受的力。

9－1在图示系统中，均质杆OA 、AB 与均质轮的质量均为m ，OA 杆的长度为1l ，AB 杆的长度为2l ，轮的半径为R ，轮沿水平面作纯滚动。

在图示瞬时，OA 杆的角速度为ω，求整个系统的动量。

ω125ml ，方向水平向左题9－1图 题9－2图9－2 如图所示，均质圆盘半径为R ，质量为m ，不计质量的细杆长l ，绕轴O 转动，角速度为ω，求下列三种情况下圆盘对固定轴的动量矩： （a ）圆盘固结于杆；（b ）圆盘绕A 轴转动，相对于杆OA 的角速度为ω-； （c ）圆盘绕A 轴转动，相对于杆OA 的角速度为ω。

（a ）ω)l R (m L O 222+=；（b ）ω2ml L O =；（c ）ω)l R (m L O 22+= 9－3水平圆盘可绕铅直轴z 转动，如图所示，其对z 轴的转动惯量为z J 。

一质量为m 的质点，在圆盘上作匀速圆周运动，质点的速度为0v ，圆的半径为r ，圆心到盘中心的距离为l 。

开始运动时，质点在位置0M ，圆盘角速度为零。

求圆盘角速度ω与角ϕ间的关系，轴承摩擦不计。

9－4如图所示，质量为m 的滑块A ，可以在水平光滑槽中运动，具有刚性系数为k 的弹簧一端与滑块相连接，另一端固定。

杆AB 长度为l ，质量忽略不计，A 端与滑块A 铰接，B 端装有质量1m ，在铅直平面内可绕点A 旋转。

设在力偶M 作用下转动角速度ω为常数。

求滑块A 的运动微分方程。

t l m m m x m m kxωωsin 2111+=++9－5质量为m，半径为R的均质圆盘，置于质量为M的平板上，沿平板加一常力F。

设平板与地面间摩擦系数为f，平板与圆盘间的接触是足够粗糙的，求圆盘中心A点的加速度。

9－6均质实心圆柱体A 和薄铁环B 的质量均为m ，半径都等于r ，两者用杆AB 铰接，无滑动地沿斜面滚下，斜面与水平面的夹角为θ，如图所示。

如杆的质量忽略不计，求杆AB 的加速度和杆的内力。

θsin 74g a =； 9－7均质圆柱体A 和B 的质量均为m ，半径为r ，一绳缠在绕固定轴O 转动的圆柱A 上，绳的另一端绕在圆柱B 上，如图所示。