初一数学证明题汇集

初中数学所有证明题归纳一、证明两线段相等1.两全等三角形中对应边相等。

2.同一三角形中等角对等边。

3.等腰三角形顶角的平分线或底边的高平分底边。

4.平行四边形的对边或对角线被交点分成的两段相等。

5.直角三角形斜边的中点到三顶点距离相等。

6.线段垂直平分线上任意一点到线段两段距离相等。

7.角平分线上任一点到角的两边距离相等。

8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。

9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。

10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。

11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。

12.两圆的内(外)公切线的长相等。

13.等于同一线段的两条线段相等。

二、证明两个角相等1.两全等三角形的对应角相等。

2.同一三角形中等边对等角。

3.等腰三角形中，底边上的中线(或高)平分顶角。

4.两条平行线的同位角、内错角或平行四边形的对角相等。

5.同角(或等角)的余角(或补角)相等。

6.同圆(或圆)中，等弦(或弧)所对的圆心角相等，圆周角相等，弦切角等于它所夹的弧对的圆周角。

7.圆外一点引圆的两条切线，圆心和这一点的连线平分两条切线的夹角。

8.相似三角形的对应角相等。

9.圆的内接四边形的外角等于内对角。

10.等于同一角的两个角相等。

三、证明两条直线互相垂直1.等腰三角形的顶角平分线或底边的中线垂直于底边。

2.三角形中一边的中线若等于这边一半，则这一边所对的角是直角。

3.在一个三角形中，若有两个角互余，则第三个角是直角。

4.邻补角的平分线互相垂直。

5.一条直线垂直于平行线中的一条，则必垂直于另一条。

6.两条直线相交成直角则两直线垂直。

7.利用到一线段两端的距离相等的点在线段的垂直平分线上。

8.利用勾股定理的逆定理。

9.利用菱形的对角线互相垂直。

10.在圆中平分弦(或弧)的直径垂直于弦。

11.利用半圆上的圆周角是直角。

初中数学命题与证明专题训练50题含参考答案一、单选题1．如图，已知AC 与BD 相交于点O ，OE 是AOD ∠的平分线，可以作为假命题“相等的角是对顶角”的反例的是( )A ．AOB DOC ∠=∠ B ．EOC DOC ∠<∠ C ．EOB EOC ∠=∠D ．EOC DOC ∠>∠2．下列四个命题①过一点有且只有一条直线与已知直线垂直；①两条直线被第三条直线所截，内错角相等；①一个正实数的算术平方根一定是正实数；①2-是4的平方根，其中真命题的个数为（ ） A ．1个B ．2个C ．3个D ．4个3．下列命题的逆命题不正确的是（ ） A ．全等三角形的对应边相等 B ．直角三角形两锐角互余 C ．如果,a b =那么22a b = D ．两直线平行，同旁内角互补4．下列命题中假命题是（ ） A ．对顶角相等B ．直线5y x =-不经过第二象限C ．两直线平行，内错角相等D ．两个锐角的和是钝角5．下列命题中，是真命题的是（ ） A ．对角线互相垂直的平行四边形是正方形 B ．相似三角形的周长之比等于相似比的平方C ．若（1，1y ）、（2，2y ）是双曲线1y x=-上的两点，则1y <2yD ．方程2230x x -+=有两个不相等的实数根 6．下列命题是真命题的是（ ） A ．如果a +b ＝0，那么 a ，b 互为相反数 B ．同位角相等C ．过一点有且只有一条直线与已知直线平行D ．两条直线被第三条直线所截，内错角相等7．有下列命题：①方程240x -=的解是2x =；①64的平方根是±8；①两边和它们的夹角对应相等的两个三角形全等；①若22a b =，则a b =；①1x >.其中假命题有（ ）A ．4个B ．3个C ．2个D ．1个8．说明命题“如果01n <<，那么210n ->”是假命题的一个反例可以是（ ） A ．12n =B ．12n =-C ．2n =D ．2n =-9．下列语句中，不属于命题的个数是( )①延长线段AB ；②自然数都是整数；③两个锐角的和一定是直角；④同角的余角相等． A ．1B ．2C ．3D ．410．下列命题是假命题的是（ ）A ．如果两角相等，那么它们一定是对顶角B ．等角（同角）的余角相等C ．等腰三角形两底角相等D ．全等三角形面积相等11．对于四边形的以下说法：①对角线互相平分的四边形是平行四边形； ①对角线相等且互相平分的四边形是矩形； ①对角线垂直且互相平分的四边形是菱形；①顺次连结对角线相等的四边形各边的中点所得到的四边形是矩形． 其中你认为正确的个数有（ ） A ．1个B ．2个C ．3个D ．4个12．下列命题：①如果一个数的相反数等于它本身，则这个数是0；①在三角形中，连接一个顶点和对边中点直线叫做三角形的中线；①任何三角形都有三条中线、三条内角平分线、三条高线，它们都相交于一点；①直角三角形的高只有一条.①三角形的三条高所在的直线相交于一点，这一点不在三角形的内部，就在三角形的外部；①一个数的算术平方根等于它本身，则这个数是1或0；其中真命题有（ ）. A ．1个B ．2个C ．3个D ．4个13．下列命题是假命题的是（ ） A ．若x ＜y ，则x +2008＜y +2008B ．单项式2347x y -的系数是﹣4C ．若|x ﹣1|+（y ﹣3）2＝0则x ＝1，y ＝3D ．平移不改变图形的形状和大小 14．下列命题中，假命题．．．是（ ）A ．2-的绝对值是2-B ．对顶角相等C ．平行四边形是中心对称图形D ．如果直线,a c b c ∥∥，那么直线ab15．下列命题是假命题的是（ ） A ．对顶角相等 B ．直角三角形两锐角互余 C ．同位角相等D ．全等三角形对应角相等16．下列语句中，不是命题的是（ ） A ．相等的角都是对顶角 B ．数轴上原点右边的点 C ．钝角大于90度 D ．两点确定一条直线 17．下列命题正确的是（ ） A ．矩形的对角线互相垂直平分B ．一组对角相等，一组对边平行的四边形一定是平行四边形C ．正八边形每个内角都是145D ．三角形三边垂直平分线交点到三角形三边距离相等 18．下列说法正确的是（ ） A ．一组数据6，5，8，8，9的众数是8B ．甲、乙两组学生身高的方差分别为2 2.3S =甲，21.8S =乙．则甲组学生的身高较整齐 C ．命题“若||1a =，则1a =”是真命题 D ．三角形的外角大于任何一个内角19．可以用来证明命题“若20.01a >，则0.1a >”是假命题的反例（ ） A ．可以是a ＝－0.2，不可以是 a ＝2 B ．可以是a ＝2，不可以是 a ＝－0.2 C ．可以是a ＝－0.2，也可以是 a ＝2 D ．既不可以是a ＝－0.2，也不可以是 a＝2二、填空题20．命题“不是对顶角的两个角不相等”的逆命题是__________．21．已知：在△ABC 中，AB ≠AC ，求证：①B ≠①C ．若用反证法来证明这个结论，可以假设__________．22．把命题“三边分别相等的两个三角形全等”写成“如果⋯⋯那么⋯⋯”的形式_____________.23．要判定一个命题是真命题，往往需要从命题的条件出发，根据已知的定义、基本事实、定理（包括推论），一步一步地推得结论成立，这样的推理过程叫做___________．要说明一个命题是假命题，通常可以通过___________的方法，命题的反例是具备命题的条件，但不具备命题的___________的实例．24．判断题：（1）所有的三角形都相似_____________（2）所有的梯形都相似_____________（3）所有的等腰三角形都相似_____________（4）所有的直角三角形都相似_____________（5）所有的矩形都相似_____________（6）所有的平行四边形都相似_____________（7）大小的中国地图相似_____________（8）所有的正多边形都相似_____________25．将命题“乘积为1的两个数互为倒数”改写成“如果……那么……”的形式：________________________________________________.26．命题“等腰三角形底边上的高线与中线互相重合”的逆命题是______27．把命题“等角的补角相等”改写成“如果…，那么…”的形式为________________________.题设是：________________________.结论是：________________________.28．命题“有两个角互余的三角形是直角三角形”的逆命题是_____命题.（填“真”或“假”）29．命题“如果两个实数相等，那么它们的平方相等”的逆命题是_____________________________．逆命题是______（填“真“或“假”）命题．30．命题“一组数据的中位数只有一个”是_______命题（填“真”或“假”）31．“两个无理数的积还是无理数”这句话是错误的，请举出一个反例进行说明______．32．“同位角相等，两直线平行”的逆命题是______；这是______命题（真或假）．33．命题“如果两个三角形全等，那么这两个三角形的周长相等”的逆命题是_______命题（填“真”或“假”）．34．命题“对角线相等的平行四边形是矩形”的逆命题为________________________35．命题“互为相反数的两数的和是0”的逆命题是______________，它是__命题．（填“真、假”）36．下列命题的逆命题成立的序号是____ ① 同旁内角互补，两直线平行 ① 等边三角形是锐角三角形① 如果两个实数相等，那么它们的平方相等 ① 全等三角形的三条对应边相等 37．下列说法正确的是_____（填序号）．①在同一平面内，a ，b ，c 为直线，若a ①b ，b ①c ，则a ①c ； ①“若ac ＞bc ，则a ＞b ”的逆命题是真命题；①若点M （a ，2）与N （1，b ）关于x 轴对称，则a +b ＝﹣1；a ，小数部分是b ，则ab ＝﹣3．38．根据下图和命题“等腰三角形底边上的中线是顶角的角平分线”写出：已知：_______________________________ 求证：_______________ ．三、解答题39．指出下列命题的条件和结论． （1）若a ＞0，b ＞0，则ab ＞0． （2）同角的补角相等．40．利用反证法证明：一个三角形中不能有两个角是钝角．41．如图，有如下四个论断：①AC DE ∥；①DC EF ∥；①CD 平分BCA ∠；①EF 平分BED ∠，请你选择四个论断中的三个作为条件，余下的一个论断作为结论，构成一个正确的数学命题并证明它．42．判断命题“对角线互相垂直且相等的四边形是正方形”是否成立．如果认为不成立，请增加一个条件使它成立．43．下列命题中，哪些是真命题？哪些是假命题？若是假命题，请举一反例. (1)互为邻补角的两角之和等于180°; (2)如果ab ＞0,那么a+b ＞0;(3)如果一个有理数既不是正数，也不是负数，那么它一定是0.44．先判断下列各命题的真假，然后写出它们的逆命题，并判断逆命题的真假： （1）对角线互相垂直的四边形是菱形； （2）相似四边形对应边成比例．45．指出下列命题的条件和结论，并判断命题的真假． （1）垂直于同一条直线的两条直线平行． （2）同位角相等． （3）若a 2=b 2,则a =b ．（4）两条直线相交只有一个交点．46．如图所示，D 、E 分别为①ABC 的边AB 、AC 上点，①BE 与CD 相交于点O ．现有四个条件：①AB=AC ；①OB=OC ；①①ABE=①ACD ；①BE=CD ．（1）请你选出两个条件作为题设，余下作结论，写一个正确的命题：命题的条件是_______和_______，命题的结论是_______和________（均填序号） （2）证明你写的命题．47．在四边形ABCD 中，对角线AC 与BD 相交于点O ． ①如果//AB CD ，BO DO =，那么四边形ABCD 是平行四边形； ①如果//AB CD ，ABC ADC ∠=∠，那么四边形ABCD 是平行四边形； ①如果AB CD =，BO DO =，那么四边形ABCD 是平行四边形；①如果ABC ADC=，那么四边形ABCD是平行四边形．∠=∠，BO DO（1）判断上述四个命题的真假；（2）证明上述四个命题的真假．（提示：证明一个命题是假命题，只要举个反例．）参考答案：1．C【分析】根据角平分线定义得到①AOE=①DOE，利用角的加减可得①EOB=①EOC，由于反例要满足角相等且不是对顶角，所以①EOB=①EOC可作为反例．【详解】①OE是①AOD的平分线，①①AOE=①DOE，①①AOE+①AOB=①DOE+①COD，即①EOB=①EOC可作为说明命题“相等的角是对顶角”为假命题的反例．故选：C．【点睛】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．也考查了逆命题．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．2．B【分析】直接利用垂线的性质、平行线的性质以及平方根的定义等知识分别判断得出答案．【详解】①在同一平面内，过一点有且只有一条直线与已知直线垂直，故①是假命题；①两条平行线被第三条直线所截，内错角相等，故①是假命题；①一个正实数的算术平方根一定是正实数，是真命题；①-2是4的平方根，是真命题；故选：B．【点睛】此题主要考查了命题与定理，正确掌握相关定义是解题关键．3．C【分析】把一个命题的条件和结论互换就得到它的逆命题，然后进行判断即可．【详解】解：A．全等三角形的对应边相等的逆命题是对应边相等的三角形全等，逆命题是真命题；B．直角三角形两锐角互余的逆命题是两锐角互余的三角形是直角三角形，逆命题是真命题；C．如果a＝b，那么a2＝b2的逆命题是如果a2＝b2，那么a＝b，逆命题是假命题；D ．两直线平行，同旁内角互补的逆命题是同旁内角互补，两直线平行，逆命题是真命题. 故选：C ．【点睛】考查了命题与定理的知识，解题的关键是知道如何写出一个命题的逆命题，难度不大． 4．D【分析】根据对顶角的性质，一次函数的图象与平行线的性质，锐角，钝角的定义，逐一判断选项，即可得到答案． 【详解】①对顶角相等，正确， ①原命题是真命题，①直线5y x =-不经过第二象限，正确 ①原命题是真命题， ①两直线平行，内错角相等， ①原命题是真命题，①两个锐角的和不一定是钝角， ①原命题是假命题． 故选D ．【点睛】本题主要考查判断命题的真假，掌握基本的数学定义，定理和推论，是解题的关键． 5．C【分析】根据特殊平行四边形的判定可判断A ，根据相似三角形的性质判断B ，根据反比例函数的增减性可判断C ，计算一元二次方程的判别式可判断D. 【详解】A. 对角线互相垂直的平行四边形是菱形，故A 是假命题； B. 相似三角形的周长之比等于相似比，故B 是假命题；C. 反比例函数1y x=-，k=-1＜0，所以在二、四象限内y 随x 的增大而增大，而0＜1＜2，所以1y <2y ，故C 为真命题；D. 方程2230x x -+=,=412=80∆--<，所以方程无实数根，故D 为假命题. 故选C.【点睛】本题考查真假命题的判断，熟练掌握各种基本概念和知识点是判断命题真假的关键.6．A【分析】根据相反数的定义、同位角的性质、平行的判定及性质等知识逐项判定即可． 【详解】解：A 、如果a +b ＝0，那么a ，b 互为相反数，为真命题； B 、两直线平行，同位角相等，故原命题为假命题；C 、过直线外一点有且只有一条直线与已知直线平行，故原命题为假命题；D 、两条平行直线被第三条直线所截，内错角相等，故原命题为假命题． 故选：A ．【点睛】本题考查了命题与定理的知识，解题的关键是了解相反数的定义、同位角的性质、平行的判定及性质等知识，难度不大，属于基础题． 7．B【分析】根据解一元二次方程、平方根的性质、全等三角形的判定以及二次根式有意义的条件分别进行判断即可. 【详解】易知①①是真命题，方程²40x -=的解是2x =±，故①是假命题； 取1a =，1b，则22a b =，但ab ，故①是假命题；1x ，故①是假命题. 故选B.【点睛】本题考查命题真假的判断，真命题要经过推理验证其正确性，假命题只需举出一个反例即可. 8．A【分析】根据举反例的定义：符合某个命题的条件，但不符合该命题结论的例子，即可进行解答．【详解】解：A 、当12n =时，221311024n ⎛⎫-=-=-< ⎪⎝⎭，与原命题矛盾，故原命题为假命题，符合题意；B 、12n =-不符合条件01n <<，故B 不符合题意；C 、当2n =不符合条件01n <<，故C 不符合题意；D 、2n =-不符合条件01n <<，故D 不符合题意． 故选：A ．【点睛】本题主要考查了用举反例的定义，解题的关键是熟练掌握举反例的定义：符合某个命题的条件，但不符合该命题结论的例子．9．A【详解】命题是判断一件事情的语句，①自然数都是整数；①两个锐角的和一定是直角；①同角的余角相等，都对情况作出了判断，都是命题，①延长线段AB，对情况没有作出了判断，不是命题，故选A.10．A【分析】根据对顶角的、余角与补角、全等三角形、等腰三角形的性质逐个判断即可．【详解】解：A、对顶角相等，但相等的角不一定是对顶角，故如果两角相等，那么它们一定是对顶角错误，符合题意；B、等角（同角）的余角相等，是真命题，不符合题意；C、等腰三角形两底角相等, 是真命题，不符合题意；D、全等三角形面积相等,是真命题，不符合题意；故选：A．【点睛】本题考查了判断真假命题，对顶角的、余角与补角、全等三角形、等腰三角形的性质，能够根据已有知识点判断出命题的真假是解决本题的关键．11．C【详解】题中①①①根据平行四边形、矩形、菱形的判定，是正确的，①只能判定是平行四边形而不具备矩形的条件．故选C．12．B【分析】根据相反数的定义，算术平方根的定义，以及三角形的高线，中线和角平分线的定义及性质对各小题分析判断即可得解．【详解】解：①如果一个数的相反数等于它本身，则这个数是0，正确；①在三角形中，连接一个顶点和对边中点线段叫做三角形的中线，错误；①任何三角形都有三条中线、三条内角平分线、三条高线所在的直线，它们都相交于一点，错误；①直角三角形的高有三条，故①错误；①三角形的三条高所在的直线相交于一点，可以在三角形的内部，或在三角形的外部，还可以在三角形上，故①错误；①一个数的算术平方根等于它本身，则这个数是1或0，正确；综上所述，正确的命题有①①，共2个，故选B ．【点睛】本题主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．13．B【分析】非负数的性质：几个非负数的和是0，则这几个非负数都是0；平移的性质：平移前后的两个图形全等．然后结合等式性质与单项式系数的定义进行判断.【详解】解：A 、根据不等式的性质，故正确；B 、单项式2347x y -的系数是47-，故错误； C 、若|x ﹣1|+（y ﹣3）2＝0，则x ＝1，y ＝3，故正确；D 、平移不改变图形的形状和大小，故正确．故选B ．【点睛】此题涉及面较广，涉及到等式的性质、非负数的性质、平移的性质及单项式的系数，是一道好题．14．A【分析】根据绝对值的意义，对顶角的性质，平行四边形的性质，平行线的判定逐一判断即可．【详解】解：A ． 2-的绝对值是2，故原命题是假命题，符合题意；B ．对顶角相等，故原命题是真命题，不符合题意；C ．平行四边形是中心对称图形，故原命题是真命题，不符合题意；D ． 如果直线,a c b c ∥∥，那么直线a b ，故原命题是真命题，不符合题意；故选：A ．【点睛】本题考查了命题真假的判断，属于基础题．根据定义：符合事实真理的判断是真命题，不符合事实真理的判断是假命题，不难选出正确项．15．C【分析】根据对顶角的性质、直角三角形的性质、平行线的性质、全等三角形的性质逐项判断即可得．【详解】解：A 、对顶角相等，则此项命题是真命题；B 、直角三角形两锐角互余，则此项命题是真命题；C 、两直线平行，同位角相等，则此项命题是假命题；D 、全等三角形对应角相等，则此项命题是真命题；故选：C ．【点睛】本题考查了对顶角、直角三角形的性质、平行线的性质、全等三角形的性质、命题，熟练掌握各性质是解题关键．16．B【详解】试题分析：命题是判断一件事情的语句，所以A 、C 、D 都是命题，B 不是命题，故选B ．考点：命题的概念．17．B【分析】根据矩形的性质、平行四边形的判定、多边形的内角和及三角形垂直平分线的性质，逐项判断即可．【详解】A.矩形的对角线相等且互相平分，故原命题错误；B.已知如图：A C ∠=∠，//AB CD ，求证：四边形ABCD 是平行四边形．证明：①//AB CD ，①180A D ∠+∠=︒，①A C ∠=∠，①180C D ∠+∠=︒，①//AD BC ，又①//AB CD ，①四边形ABCD 是平行四边形，①一组对角相等，一组对边平行的四边形一定是平行四边形，故原命题正确；C.正八边形每个内角都是：()180821358︒⨯-=︒，故原命题错误； D.三角形三边垂直平分线交点到三角形三个顶点的距离相等，故原命题错误．故选：B ．【点睛】本题考查命题的判断，明确矩形性质、平行四边形的判定定理、多边形内角和公式及三角形垂直平分线的性质是解题关键．18．A【分析】分别根据众数、方差、真命题、三角形外角定理等知识逐项判断即可求解．【详解】解：A.“一组数据6，5，8，8，9的众数是8”，判断正确，符合题意；B. “甲、乙两组学生身高的方差分别为2 2.3S =甲，2 1.8S =乙，则甲组学生的身高较整齐”，因为22S S 甲乙＞ ，所以乙组学生的身高较整齐，原判断错误，不合题意；C. 命题“若||1a =，则1a =±”，所以原判断错误，不合题意；D.“三角形的外角大于任何一个不相邻的内角”，所以原判断错误，不合题意．故选：A ．【点睛】本题考查了众数，方差，真假命题，三角形的外角等知识，熟知相关定理是解题关键．19．A【详解】当a= - 0.2时，a²=0.04＞0.01；a ＜0.1.当a=2时，a²=4＞0.01；a ＞0.1.于是可以证明命题“若a²＞0.01，则a ＞0.1”是假命题的反例的可以是a= - 0.2，不可以是a=2.故选A.20．不相等的两个角不是对顶角【分析】根据逆命题的概念即可得出答案．【详解】命题“不是对顶角的两个叫不相等”的逆命题是：不相等的两个角不是对顶角， 故答案为：不相等的两个角不是对顶角．【点睛】本题主要考查逆命题，掌握逆命题的写法是解题的关键．21．①B =①C【分析】反证法的步骤中，第一步是假设结论不成立，反面成立，可据此进行判断．【详解】解：①B ≠①C 的反面是①B =①C ．故可以假设①B =①C ．故答案为：①B =①C ．【点睛】本题主要考查了反证法的基本步骤，正确确定①B ≠①C 的反面，是解决本题的关键．22．如果两个三角形三条边对应相等，那么这两个三角形全等【分析】命题一般都可以写成如果…那么…形式；如果后面是题设，那么后面是结论．【详解】把命题“三边分别相等的两个三角形全等”写成“如果⋯⋯那么⋯⋯”的形式为：如果两个三角形三条边对应相等，那么这两个三角形全等.故答案为：如果两个三角形三条边对应相等，那么这两个三角形全等23．证明举反例结论【分析】根据根据证明的概念和举反例的概念直接填空即可．．【详解】解：要判定一个命题是真命题，往往需要从命题的条件出发，根据已知的定义、基本事实、定理（包括推论），一步一步地推得结论成立，这样的推理过程叫做证明．要说明一个命题是假命题，通常可以通过举反例的方法，命题的反例是具备命题的条件，但不具备命题的结论的实例．故答案为：证明；举反例；结论．【点睛】本题主要考查了证明和举反例的概念，熟知相关知识是解题的关键．24．错误错误错误错误错误错误正确错误【分析】相似图形是指形状相同的图形．对多边形进行判断时，主要是看对应角是否相等，对应边的比是否相等．【详解】（1）所有的三角形，不能判断它们的对应角相等，对应边的比相等，不是相似形．所以（1）错误．（2）所有的梯形，不能判断对应的角相等，对应边的比相等，不是相似形．所以（2）错误．（3）所有的等腰三角形，不能判断对应的角相等，对应边的比相等．所以（3）错误．（4）所有的直角三角形，不能判断对应的角相等，对应边的比相等．所以（4）错误．（5）所有的矩形，不能判断对应的角相等，对应边的比相等．所以（5）错误．（6）所有的平行四边形，不能判断对应的角相等，对应边的比相等．所以（6）错误．（7）大小的中国地图，只是大小不等，性质相同，是相似形．所以（7）正确．（8）所有的边数相等的正多边形才相似．所以（8）错误．故答案是：（1）错误，（2）错误，（3）错误，（4）错误，（5）错误，（6）错误，（7）正确，（8）错误．【点评】本题考查的是相似图形，根据相似图形的定义对多边形是否相似进行判断．25．如果两个数的乘积为1，那么这两个数互为倒数【详解】试题解析：乘积为1的两个数互为倒数”改写成“如果……那么……”的形式为：如果两个数的乘积为1，那么这两个数互为倒数.故答案为如果两个数的乘积为1，那么这两个数互为倒数.26．如果一个三角形一边上的高线与中线互相重合，那么这个三角形是等腰三角形【分析】根据逆命题的定义：对于两个命题，如果一个命题的条件和结论分别是另外一个命题的结论和条件，那么这两个命题叫做互逆命题，找出已知命题的题设和结论，即可写出其逆命题．【详解】解：“等腰三角形底边上的高线与中线互相重合”的题设为：如图一个三角形是等腰三角形，结论为：那么它底边上的高线和中线互相重合①该命题的逆命题为：如果一个三角形一边上的高线与中线互相重合，那么这个三角形是等腰三角形故答案为：如果一个三角形一边上的高线与中线互相重合，那么这个三角形是等腰三角形．【点睛】此题考查的是写一个命题的逆命题，掌握逆命题的定义是解决此题的关键．27．如果两个角相等，那么这两个角的补角相等两个角相等这两个角的补角相等【分析】根据任何一个命题都可以写成“如果…，那么…”的形式如果后面是题设，那么后面是结论，进而得出答案即可.【详解】命题“等角的补角相等”的题设是“两个角相等”，结论是“这两个角的补角相等”．故命题“等角的补角相等”写成“如果…，那么…”的形式是：如果两个角相等，那么这两个角的补角相等．故答案为如果两个角相等，那么这两个角的补角相等；两个角相等；这两个角的补角相等．【点睛】本题考查了命题的改写问题．找准原命题的题设与结论是正确解答本题的关键．命题的一般叙述形式为“如果…..，那么……”，其中，“如果”所引出的部分是题设（条件），“那么”所引出的部分是结论.28．真；【分析】命题“有两个角互余的三角形是直角三角形”的题设为三角形中有两个锐角互余，结论为这个三角形为直角三角形，然后交换题设与结论即可得到原命题的逆命题，然后再判断出命题的真假．【详解】“有两个角互余的三角形是直角三角形”的逆命题“直角三角形的两个锐角互余”，是真命题．故答案为真.【点睛】本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．也考查了逆命题．29．如果两个实数的平方相等，那么这两个实数相等假【分析】逆命题即将原命题的结论变为已知，原命题的已知变为结论，若22a b=，则a和b可能相等，也可能互为相反数；【详解】逆命题为：如果两个实数它们的平方相等，那么这两个实数相等，若22=，则a ba和b可能相等，也可能互为相反数，所以是假命题；故答案是：如果两个实数它们的平方相等，那么这两个实数相等；假．【点睛】本题主要考查了命题与定理，准确分析判断是解题的关键．30．真【分析】根据中位数的计算方法判断即可．【详解】解：①中位数是将一组数据按照由小到大（或由大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数；①中位数的位置是确定的，①一组数据的中位数只有一个，故答案为：真；【点睛】本题考查了真命题（正确的命题），中位数的定义；掌握中位数的计算方法是解题关键．3122==（答案不唯一）【分析】根据无理数的乘法运算法则，即可求解．【详解】解：“两个无理数的积还是无理数”这句话是错误的，举反例如下：2=．22（答案不唯一）【点睛】此题比较灵活地考查了无理数的有关运算，需考虑到无理数相乘的特殊情况．32．两直线平行，同位角相等真【分析】交换原命题的题设与结论即可得到其逆命题，然后根据平行线的性质判断逆命题的真假．。

初一下数学证明题(精选多篇)第一篇：初一下数学证明题初一下数学证明题6、如图，ce平分∠acb且ce⊥bd，∠dab=∠dba，ac=18，△cdb的周长是28。

求bd的长大家看我的步骤，我的步骤只做到这里就坐不下去了解：因为∠dab=∠dba(已知)所以ad=bd(等角对等边)因为ce平分∠acb，ce⊥bd(已知)所以∠dce=∠bce(角平分线的意义)∠bec=∠dec=90度(垂直意义)在△ace与△bce中因为{∠dce=∠bce(已求){ce=ec(公共边){∠bec=∠dec(已求)所以△ace≌△bce(a.s.a)所以bc=cd(全等三角形对应边相等)因为ac=18,即cd+ad=18所以cd+bd=18因为△cdb的周长是28，即cd+bd+bc=28所以bc=28-18=10所以cd=10所以bd=18-10=82在△abc中，已知∠cab=60°，d，e分别是边ab，ac上的点，且∠aed=60°，ed+db=ce，∠cdb=2∠cde，则∠dcb=()a.15°b.20°c.25°d.30°这题实际上是一传统题的翻版，原题中条件为△ade为等边三角形，c，b分别是ae，ad延长线的点，且ec=ab，求证;cd=cb，结论明确，本题增加了一个条件∠cdb=2∠cde，把结论改为求值题，其它改动没有多大变化，很快就会知道△ade为等边三角形，ec=ab，∠edc=∠cdb/2=40°，但结论为求值题后使结论没有目标，实际上是故弄玄虚，习难学生，使分析没有方向，要是学生没做过原题要得出正确结论是不大可能的!但学生可做一下投机;地图作得尽量正确，用量角器测一下也可得正确的结论。

但我觉得不会是供题者的本意吧。

故我认为对本题的改动看起来是改革，实为一败笔!不可取!但本题的原题我认为是一个能提高学生学习数学的兴趣与陪养学生创造性思维的好题题，现就原题给出若干分析请于指正。

七年级证明题及答案【篇一：七年级数学证明题专练】p> xxx年级xx班级姓名：_______________班级：_______________考号：_______________一、简答题（每空？分，共？分）1、如图，已知∠b =∠c，∠1 =∠2，可推得ab∥cd。

理由如下：=∠2（已知），且∠1 =∠cgd（__________________________）∴∠2 =∠cgd （等量代换）∴ce∥bf（_______________________________）∴∠ =∠bfd（__________________________）又∵∠b =∠c（已知）∴∠bfd =∠b（）∴ab∥cd（________________________________）2、说理过程填空（每空1分，共5分）已知：∠bcf=∠b+∠f。

试说明：ab//ef理由：经过点c作cd//ab∴∠bcd=∠b（）∵∠bcf=∠b+∠f（已知）∴∠（）=∠f（）∴cd//ef（）∴ab//ef（）3、如图，ab∥cd，bn、dn分别平分∠abm、∠mdc，试问∠bmd与∠bnd之间的数量关系如何？证明你的结论．5、如图，已知be∥df，∠b＝∠d，则ad与bc平行吗?试说明理由．（8分）二、填空题（每空？分，共？分）6、在等腰rt△abc中。

ac=bc，以斜边ab为一边作等边△abd．使点c、d在ab的同侧，再以cd为一边作等边△cde，使得c、e在ad 的异侧，若ae=1，则cd的长为。

三、选择题（每空？分，共？分）7、如图所示，ab=bc=cd=de=1，ab⊥bc、ac⊥cd，ad⊥de，则ae等于（）a．1 b． c．d．28、园丁住宅小区有一块草坪如图所示．已知ab=3m，bc=4m，cd=12m，da=13m，且ab⊥bc，这块草坪的面积是( ) a．24m b．36m c．48m d．72m22229、2002年8月在北京召开的国际数学家大会会标如图所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形。

第 6 页 共 15 页
4.如下图连接 AC 并取其中点 Q，连接 QN 和 QM，所以可得∠QMF=∠F，∠QNM=∠
DEN 和∠QMN=∠QNM，从而得出∠DEN＝∠F。
经 典 题（二）
1.(1)延长 AD 到 F 连 BF，做 OG⊥AF,
又∠F=∠ACB=∠BHD， 可得 BH=BF,从而可得 HD=DF， 又 AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM
BE AD
= ，即 AD•BC=BE•AC，
①
BC AC
又∠ACB=∠DCE，可得△ABC∽△DEC，既得
AB = DE ，即 AB•CD=DE•AC，
②
AC DC
由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ，得证。
第 11 页 共 15 页
4.过 D 作 AQ⊥AE
(2)连接 OB，OC,既得∠BOC=1200，
从而可得∠BOM=600, 所以可得 OB=2OM=AH=AO, 得证。
第 7 页 共 15 页
3.作 OF⊥CD，OG⊥BE，连接 OP，OA，OF，AF，OG，AG，OQ。 由于 AD = AC = CD = 2FD = FD ， AB AE BE 2BG BG
（2）过 P 点作 BC 的平行线交 AB,AC 与点 D，F。
由于∠APD>∠ATP=∠ADP，
推出 AD>AP
①
又 BP+DP>BP
②
和 PF+FC>PC
③
又 DF=AF
④
由①②③④可得：最大 L< 2 ；

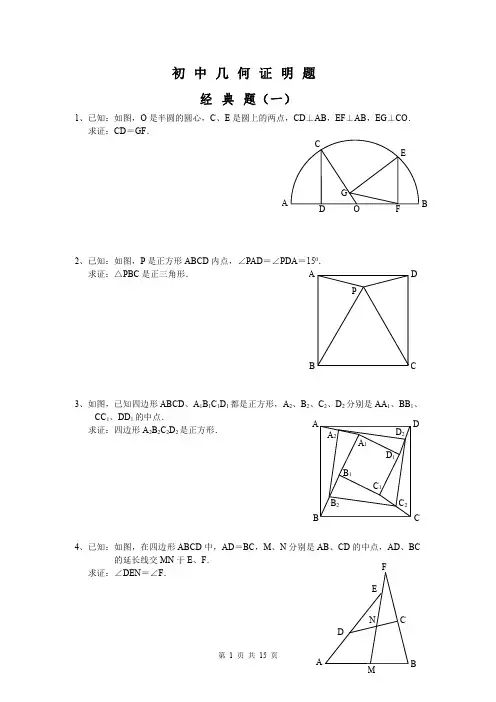
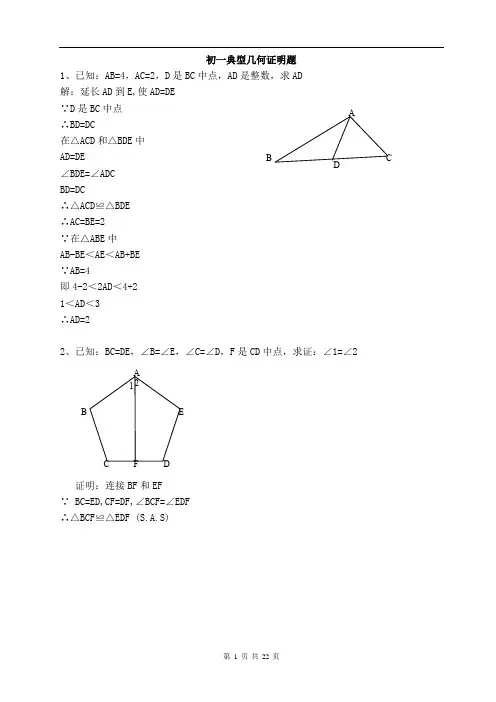
初一典型几何证明题1、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=22、已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。

∴ ∠BAF=∠EAF (∠1=∠2)。

3、已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF，可得，∠EFD＝CGD DE ＝DC∠FDE＝∠GDC（对顶角） ∴△EFD≌△CGD EF ＝CG ∠CGD＝∠EFD 又，EF∥AB ∴，∠EFD＝∠1 ∠1=∠2 ∴∠CGD＝∠2∴△AGC 为等腰三角形， AC ＝CG 又 EF ＝CG ∴EF ＝AC4、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CBA CDF2 1 EA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5、已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6、如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

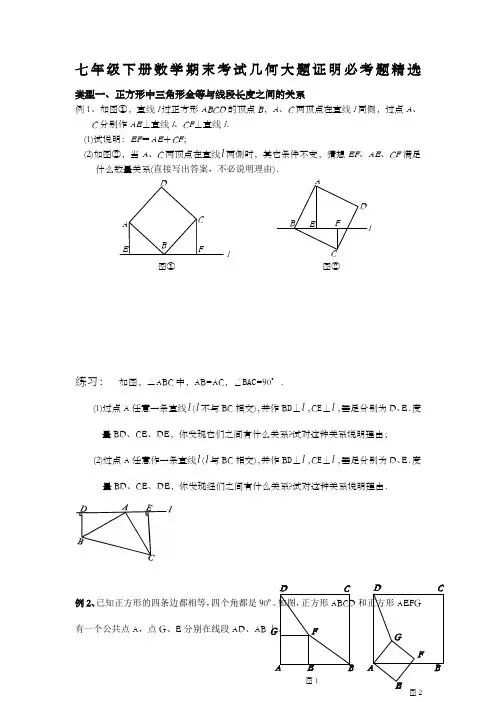
图①DA EC BFl图②ABE F ClD七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①，直线l 过正方形ABCD 的顶点B ，A 、C 两顶点在直线l 同侧，过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l ． (1)试说明：EF ＝AE ＋CF ；(2)如图②，当A 、C 两顶点在直线l 两侧时，其它条件不变，猜想EF 、AE 、CF 满足什么数量关系(直接写出答案，不必说明理由)．练习： 如图，△ABC 中，AB=AC ，∠BAC =90°．(1)过点A 任意一条直线l (l 不与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现它们之间有什么关系?试对这种关系说明理由； (2)过点A 任意作一条直线l (l 与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现经们之间有什么关系?试对这种关系说明理由．例2、已知正方形的四条边都相等，四个角都是90º。

如图，正方形ABCD 和正方形AEFG 有一个公共点A ，点G 、E 分别在线段AD 、AB 上。

A E B 图1D CG FA BD CG FE图2（1）如图1， 连结DF 、BF ，说明：DF ＝BF ； （2）若将正方形AEFG 绕点A 按顺时针方向旋转，连结DG ，在旋转的过程中，你能否找到一条长度与线段DG 的长始终相等的线段？并以图2为例说明理由。

练习：如图，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，B 、C 、G 三点在一条直线上，且边长分别为2和3，在BG 上截取GP ＝2，连结AP 、PF. （1）观察猜想AP 与PF 之间的大小关系，并说明理由.（2）图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形？若存在，请说明变换过程；若不存在，请说明理由.（3）若把这个图形沿着PA 、PF 剪成三块，请你把它们拼成一个大正方形，在原图上画出示意图，并请求出这个大正方形的面积.附加：如图，△ABC 与△ADE 都是等边三角形，连结BD 、CE（1）BD 与CE 相等吗？请说明理由．A BCFDE GP32B（2）你能求出BD与CE的夹角∠BFC的度数吗？（3）若将已知条件改为：四边形ABCD与四边形AEFG都是正方形，连结BE、DG交点记为点M（如图）．请直接写出线段BE和DGF例3、正方形四边条边都相等，四个角都是90o．如图，已知正方形ABCD在直线MN 的上方，BC在直线MN上，点E是直线MN上一点，以AE为边在直线MN的上方作正方形AEFG．（1）如图1，当点E在线段BC上（不与点B、C重合）时：①判断△ADG与△ABE是否全等，并说明理由；②过点F作FH⊥MN，垂足为点H，观察并猜测线段BE与线段CH的数量关系，并说明理由；（2）如图2，当点E在射线CN上（不与点C重合）时：①判断△ADG与△ABE是否全等，不需说明理由；②过点F 作FH ⊥MN ，垂足为点H ，已知GD ＝4，求△CFH 的面积．练习：如图1，四边形ABCD 是正方形，G 是CD 边上的一个点(点G 与C 、D 不重合)，以CG 为一边作正方形CEFG ，连结BG ，DE ．（1）如图1，说明BG= DE 的理由（2）将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度 ，得到如图2．请你猜想①BG= DE 是否仍然成立？②BG 与DE 位置关系？并选取图2验证你的猜想．图 2FG DA图 1FDA类型二、探究题例1、如图，已知等边△A B C 和点P ，设点P 到△A B C 三边A B 、A C 、B C （或其延长线）的距离分别为h 1、h 2、h 3，△A B C 的高为h ．在图（1）中，点P 是边B C 的中点，此时h 3=0，可得结论：h h h h =++321． 在图（2）--（5）中，点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外．（1）请探究：图（2）--（5）中， h 1、h 2、h 3、h 之间的关系；（直接写出结论）（2）证明图（2）所得结论； （3）证明图（4）所得结论．（4）（附加题2分）在图（6）中，若四边形R B C S 是等腰梯形，∠B =∠C =60o ，R S =n ，B C =m ，点P 在梯形内，且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4，桥形的高为h ，则h 1、h 2、h 3、h 4、h 之间的关系为： ；图（4）与图（6）中的等式有何关系？ABC DEPM(3)ABCDE (2)ABCD EM (P )(1)练习：1、如图，在△ABC 中，AB=AC ，P 为底边上任意一点，PE ⊥AB ，PF ⊥AC ，BD ⊥AC.（1）求证：PE+PF=BD ；（2）若点P 是底边BC 的延长线上一点，其余条件不变，（1）中的结论还成立吗？如果成立，请说明理由；如果不成立，请画出图形，并探究它们的关系.CBAPDE2、如图，已知△ABC 三边长相等，和点P ，设点P 到△ABC 三边AB 、AC 、BC （或其延长线）的距离分别为h 1、h 2、h 3，△ABC 的高为h ．在图（1）中， 点P 是边BC 的中点，由S △ABP+S △ACP=S △ABC 得，h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0，所以：h h h h =++321．图（2）~（5）中，点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外．（1）请探究：图（2）~（5）中， h 1、h 2、h 3、h 之间的关系；（直接写出结论）⑵ ⑶ ⑷ ⑸ （2）说明图（2）所得结论为什么是正确的； （3）说明图（5）所得结论为什么是正确的．ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)ABCDEP M(5)FC B E 例2、已知△ABC 是等边三角形，将一块含30o 角的直角三角板DEF 如图1放置，当点E 与点B 重合时，点A 恰好落在三角板的斜边DF 上. （1）AC=CF 吗? 为什么?（2）让三角板在BC 上向右平行移动，在三角板平行移动的过程中，(如图2)是否存在与线段EB 始终相等的线段（设AB ，AC 与三角板斜边的交点分别为G ，H ）？如果存练习：1、如图1，一等腰直角三角尺GEF （∠EGF=90°,∠GEF=∠GFE=45°,GE=GF ）的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 相等吗？并说明理由；（2）若三角尺GEF 旋转到如图3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立C图1吗？请说明理由．2、已知：△ABC 为等边三角形，M 是BC 延长线上一点，直角三角尺的一条直角边经过点A ，且60º角的顶点E 在BC 上滑动，（点E 不与点B 、C 重合），斜边∠ACM 的平分线CF 交于点F（1）如图（1）当点B 在BC 边得中点位置时（6分） ○1猜想AE 与BF 满足的数量关系是 。

初一数学三角形证明题1. 证明三角形内角和等于180度证明我们知道，三角形有三个内角，分别为角A、角B和角C。

要证明三角形的内角和等于180度，我们可以使用下面的方法：1. 假设角A的度数为x度。

2. 根据三角形的定义，角A、角B和角C的度数相加等于180度。

3. 根据假设，我们可以得到下面的等式：x + 角B + 角C = 180度。

4. 将等式两边的x相消，我们得到：角B + 角C = 180度 - x度。

5. 角B + 角C的度数等于180度减去角A的度数，即180度 -x度。

6. 根据三角形定义，角A的度数加上角B和角C的度数等于180度。

7. 将等式两边的角A的度数相消，我们得到：角B + 角C =180度。

8. 因此，我们可以证明三角形的内角和等于180度。

2. 证明等腰三角形底角相等证明等腰三角形是一种特殊的三角形，其中两条边的长度相等。

我们要证明等腰三角形的底角相等，可以使用下面的方法：1. 假设等腰三角形的两边长度相等，分别为a。

2. 由于等腰三角形的两边相等，所以其底边也相等。

3. 假设等腰三角形的底角分别为角A和角B。

4. 我们可以得到下面的等式：角A + 底角 + 角B = 180度。

5. 底角的度数等于180度减去角A和角B的度数。

6. 由于等腰三角形的底边相等，所以角A和角B的度数相等。

7. 角A和角B的度数相等，所以底角的度数也相等。

8. 因此，我们可以证明等腰三角形的底角相等。

这些证明题可以帮助学生巩固对三角形的性质和定义的理解，同时培养他们的逻辑思维能力和推理能力。

通过练习和理解三角形的证明题，学生可以更好地掌握数学知识。

证明题七年级下册一、相交线与平行线证明题。

1. 如图，已知直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠2 : ∠1 = 4:1，求∠AOF的度数。

证明：设∠1 = x，因为∠2:∠1 = 4:1，则∠2 = 4x。

因为OE平分∠BOD，所以∠DOE=∠1 = x。

又因为∠2+∠DOE = 180°（邻补角之和为180°），即4x + x=180°，5x = 180°，解得x = 36°。

所以∠COE=180° - ∠1=180° - 36° = 144°。

因为OF平分∠COE，所以∠COF=(1)/(2)∠COE=(1)/(2)×144° = 72°。

∠AOC = ∠1 = 36°（对顶角相等）所以∠AOF=∠AOC + ∠COF = 36°+72° = 108°。

2. 已知：如图，AB∥CD，∠1 = ∠2，求证：AM∥CN。

证明：因为AB∥CD，所以∠EAB = ∠ACD（两直线平行，同位角相等）。

又因为∠1 = ∠2，所以∠EAB - ∠1=∠ACD - ∠2，即∠MAC = ∠NCA。

所以AM∥CN（内错角相等，两直线平行）3. 如图，已知∠1 = ∠2，∠C = ∠D，求证：∠A = ∠F。

证明：因为∠1 = ∠2，∠1 = ∠3（对顶角相等），所以∠2 = ∠3。

所以DB∥EC（同位角相等，两直线平行）。

所以∠D = ∠4（两直线平行，同位角相等）。

又因为∠C = ∠D，所以∠C = ∠4。

所以DF∥AC（内错角相等，两直线平行）。

所以∠A = ∠F（两直线平行，内错角相等）二、三角形证明题。

4. 在△ABC中，AD是BC边上的中线，E是AD的中点，BE的延长线交AC于F。

求证：AF=(1)/(3)AC。

证明：过点D作DG∥BF交AC于G。

七年级数学证明题试题及参考答案七年级学习的一个难点就是证明题，这类的证明题有哪些值得推荐的呢?下面就是学习啦给大家的七年级证明题内容，希望大家喜欢。

如图AD//BC，∠A=∠C。

试说明AB//DCps：写过程..∵AD//BC∵∠A=∠ABF(两直线平行，内错角相等)∵∠A=∠C∵∠C=∠ABF∴AB//DC(同位角相等，两直线平行∵AD//BC(已知)∴∠A+∠ABC=180°(两直线平行，同旁内角互补)∵∠A=∠C(已知)∴∠C+∠ABC=180°(等式的性质)∴AB//DC(同旁内角互补，两直线平行))在正方形ABCD中，p(p靠近是D点)CD上的一点，BE⊥AP于E，DF⊥AP于F，说明△AFD≌△BEAD--------C111111∠BAE与∠DAF互余∠ADF与∠DAF互余所以∠BAE=∠ADF又待证明的两三角形都是Rt三角形，且AB=DA根据角角边定理，两三角形全等∠A=75°第二题是不是有问题啊∠GQD是30°吗应该是∠GQH=30°吧还有不懂怎么算的你追问一下我们QQ聊补充回答：∵GA//ED∴∠EBF=∠FHG=30°(两只线平行，同位角相等)∴∠FBA=∠ABD=(180°-30°)÷2=75°∵∠AHB=∠FHG=30°(对顶角)∴∠a=180°-75°-30°=75°#FormatImgID_0#还有一题等等啊补充回答：∵MN⊥CD∴∠MHD=90°∵∠GQD=130°∴∠GQH=180°-130°=50°∴∠HGQ=180°-90°-50°=40°∴∠AGH=90°∴∠EGA=180°-90°-40°=50°一、选择题(共27小题)1.﹣2的倒数是( )A.﹣B.C.2D.﹣22.﹣7的倒数是( )A.﹣B.7C.D.﹣73.﹣5的倒数是( )A.﹣5B.C.D.54.﹣2的倒数为( )A.﹣B.C.2D.15.﹣3的倒数是( )A.B.﹣3C.3D.6.﹣6的倒数是( )A.B.﹣C.6D.﹣67.与﹣3互为倒数的是( )A.﹣B.﹣3C.D.38.﹣的倒数等于( )A.B.﹣C.﹣2D.29.2的倒数是( )A.B.﹣C.±D.210.3的倒数是( )A.B.﹣C.﹣3D.311.﹣3的倒数是( )A.﹣3B.3C.D.﹣12.xx的倒数是( )A.B.﹣C.|xx|D.﹣xx13.﹣的倒数是( )A.﹣4B.4C.D.﹣14.﹣3的倒数是( )A.3B.C.﹣D.﹣315.﹣2的倒数是( )A.B.﹣C.2D.﹣216.﹣6的倒数是( )A.﹣6B.6C.D.17.﹣5的倒数是( )A.5B.﹣5C.D.﹣18.﹣的倒数是( )A.B.﹣2C.2D.﹣19.﹣的倒数是( )A.3B.﹣3C.﹣D.20.的倒数是( )A.2B.﹣2C.D.﹣21.有理数﹣的倒数是( )A.B.﹣C.D.﹣22.﹣2的倒数是( )A.2B.C.﹣D.﹣0.223.﹣的倒数是( )A.﹣3B.3C.﹣D.1、运送29.5吨煤,先用一辆载重4吨的汽车运3次,剩下的用一辆载重为2.5吨的货车运.还要运几次才能完?还要运x次才能完29.5-3*4=2.5x17.5=2.5xx=7还要运7次才能完2、一块梯形田的面积是90平方米,上底是7米,下底是11米,它的高是几米?它的高是x米x(7+11)=90*218x=180x=10它的高是10米3、某车间计划四月份生产零件5480个.已生产了9天,再生产908个就能完成生产计划,这9天中平均每天生产多少个?这9天中平均每天生产x个9x+908=54089x=4500x=500这9天中平均每天生产500个4、甲乙两车从相距272千米的两地同时相向而行,3小时后两车还相隔17千米.甲每小时行45千米,乙每小时行多少千米?乙每小时行x千米3(45+x)+17=2723(45+x)=25545+x=85x=40乙每小时行40千米5、某校六年级有两个班,上学期级数学平均成绩是85分.已知六(1)班40人,平均成绩为87.1分;六(2)班有42人,平均成绩是多少分?平均成绩是x分40*87.1+42x=85*823484+42x=697042x=3486x=83平均成绩是83分6、学校买来10箱粉笔,用去250盒后,还剩下550盒,平均每箱多少盒?平均每箱x盒10x=250+55010x=800x=80平均每箱80盒7、四年级共有学生200人,课外活动时,80名女生都去跳绳.男生分成5组去踢足球,平均每组多少人?平均每组x人5x+80=2005x=160x=32平均每组32人8、食堂运来150千克大米,比运来的面粉的3倍少30千克.食堂运来面粉多少千克?食堂运来面粉x千克3x-30=1503x=180x=60食堂运来面粉60千克9、果园里有52棵桃树,有6行梨树,梨树比桃树多20棵.平均每行梨树有多少棵?平均每行梨树有x棵6x-52=206x=72x=12平均每行梨树有12棵10、一块三角形地的面积是840平方米,底是140米,高是多少米?高是x米140x=840*2140x=1680x=12高是12米猜你感兴趣：1.初一英语语法习题答案2.七年级语文试题及答案3.初一语文试卷4.初一几何证明题答案5.初一上册几何证明题。

初一典型几何证明题1、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=22、已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。

∴ ∠BAF=∠EAF (∠1=∠2)。

3、已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF，可得，∠EFD＝CGD DE ＝DC∠FDE＝∠GDC（对顶角） ∴△EFD≌△CGD EF ＝CG ∠CGD＝∠EFD 又，EF∥AB ∴，∠EFD＝∠1 ∠1=∠2 ∴∠CGD＝∠2∴△AGC 为等腰三角形， AC ＝CG 又 EF ＝CG ∴EF ＝AC4、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CBA CDF2 1 EA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5、已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6、如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

OABCDE圆有关的证明题专项练习1、如图，△ABC 内接于⊙O ，AD 是的边BC 上的高，AE 是⊙O 的直径，连BE. （1）求证：△ABE ∽△ADC ；（2）若AB=2BE=4DC=8，求△ADC 的面积.2、如图，AE 是△ABC 外接圆⊙O 的直径，AD 是△ABC 的边BC 上的高， EF ⊥BC ，F 为垂足。

（1）求证：BF=CD（2）若CD=1，AD=3，BD=6，求⊙O 的直径。

5、如图，AB 是⊙O 的直径，D 是AB 上一点，D 是弧BC 的中点，AD 、BC 交于点E ，CF ⊥AB 于F ，CF 交AD 于G 。

（1）求证：AD =2CF ；（2）若AD=34，BC =62，求⊙O 的半径6、如图，AB 为⊙O 的直径，弦CD ⊥AB 于点H ，E 为AB 延长线上一点，CE 交⊙O 于F 。

（1）求证：BF 平分∠DFE ；（2）若EF=DF=4，BE=5，CH=3，求⊙O 的半径7、如图，Rt △ABC 内接于⊙O ，D 为弧AC 的中点，DH ⊥AB 于点H ，延长BC 、HD 交于点E 。

（1）求证：AC=2DH ；（2）连接AE ，若DH=2，BC=3，求tan ∠AEB 的值8、在Rt △ABC 中，∠ACB=90º，D 是AB 边上一点，以BD 为直径的⊙O 与边AC 相切于点E ，连结DE 并延长，与BC 的延长线交于点F ． （1）求证：BD=BF ；（2）若BC=6，AD=4，求ECF S 。

9、如图，⊙O 中， 直径DE ⊥弦AB 于H 点，C 为圆上一动点，AC 与DE 相交于点F 。

(1)求证△AOG ∽△FAO 。

(2)若OA=4，OF=8，H 点为OD 的中点，求CGF S 。

10、如图，在⊙O 中，弦AB 、CD 相交于AB 的中点E ，连接AD 并延长至F 点，使DF=AD,连接BC 、BF 。

（1）、求证：△CBE ∽△AFB 。

F A B DEC ED C BAE O D C B A 初一七年级数学几何证明题经典练习题1.如图，在ABC 中，D 在AB 上，且ΔCAD 和ΔCBE 都是等边三角形，求证：（1）DE=AB ，（2）∠EDB=60°2.如图，在ΔABC 中，AD 平分∠BAC ，DE||AC,EF ⊥AD 交BC 延长线于F 。

求证： ∠FAC=∠B3.已知，如图，在△ ABC 中，AD ，AE 分别是 △ ABC 的高和角平分线，若∠B=30∠C=50°求：（1），求∠DAE 的度数。

（2） 试写出 ∠DAE 与 ∠C - ∠B 有何关系?（不必证明） 5、如图,已知DF ∥AC,∠C=∠D,你能否判断CE ∥BD?试说明你的理由6、如图,△ABC 中,D 在BC 的延长线上,过D 作DE ⊥AB 于E,交AC 于F. 已知∠A=30°,∠FCD=80°,求∠D 。

7、如图，BE 平分∠ABD ，CF 平分∠ACD ，BE 、CF 交于G ， 若∠BDC = 140°，∠BGC = 110°，则∠A ？8、如图，AD ⊥BC 于D ，EG ⊥BC 于G ，∠E =∠1，求证AD 平分∠BAC 。

ED C B AG 3219、如图，直线DE 交△ABC 的边AB 、AC 于D 、E ，交BC 延长线于F ，若∠B ＝67°，∠ACB ＝74°，∠AED ＝48°，求∠BDF 的度数.10、如图，将一副三角板叠放在一起，使直角的顶点重合于O ，则∠AOC+∠DOB11、如图，将两块直角三角尺的直角顶点C 叠放在一起.（1）若∠DCE=350，求∠ACB 的度数；（2）若∠ACB=1400，求∠DCE 的度数；（3）猜想：∠ACB 与∠DCE 有怎样的数量关系，并说明理由12、已知：直线AB 与直线CD 相交于点O ，∠BOC=45o ，（1）如图1，若EO ⊥AB ，求∠DOE 的度数；（2）如图2，若EO 平分∠AOC ，求∠DOE 的度数．13、已知AOB ∠，P 为OA 上一点． （1）过点P 画一条直线PQ ，使PQ ∥OB ； （2）过点P 画一条直线PM ，使PM ⊥OA 交OB 于点M ； （3）若︒=∠40AOB ，则=∠PMO ？ P B O A14、如图。

七年级证明题七年级上册数学证明题ab//dc(同旁内角互补，两直线平行))在正方形abcd中，p(p靠近是d点)cd上的一点，be ap于e，df ap于f，说明△afd≌△bead--------c111111a--------bbae与 daf互余adf与 daf互余所以 bae= adf又待证明的两三角形都是rt三角形，且ab=da根据角角边定理，两三角形全等a=75第二题是不是有问题啊 gqd是30 吗应该是 gqh=30 吧还有不懂怎么算的你追问一下我们qq聊补充回答：∵ga//edebf= fhg=30 （两只线平行，同位角相等）fba= abd=（180 -30 ） 2=75∵ ahb= fhg=30 （对顶角）a=180 -75 -30 =75#formatimgid_0#还有一题等等啊补充回答：∵mn cdmhd=90∵ gqd=130gqh=180 -130 =50hgq=180 -90 -50 =40∵mn abagh=90ega=180 -90 -40 =50 您已经评价过!好:0您已经评价过!不好:0您已经评价过!原创:5您已经评价过!非原创:0第一题的答案：证明：因为这是等宽带所以ag平行de所以 ebf= gof=30 ( o 是我加上去的) 因为 ebf+ fbd=180所以 fbd=180 - ebf=150因为 fba由 abd折叠而成所以 fba= abd所以 fba=150 /2=75图为 aob和 gof为对顶角所以 aob= gof=30所以 gab=180 - abf- aob=75( gab是 a)第二题的答案：因为 dqe+ cqe=180所以 cqe=180 - dqe=50图为ab mn,cd mn所以ab平行cd所以 age= cqe=50因为mn垂直ab所以 agh=90所以 ngf=180 - ega- agh=40七年级下册证明题知识点中线定理1.三角形中，连接一个顶点和它所对边的中点的线段叫做三角形的中线。

初一代数证明题1. 问题描述在初一代数学研究中，经常会遇到一些与代数相关的证明题。

本文档将介绍一些常见的初一代数证明题，并提供解题思路。

2. 证明题目题目一：证明两个相等数的和仍然相等设 $a$ 和 $b$ 为两个相等的数，即 $a = b$。

我们要证明 $a + a = b + b$。

题目二：证明两个相等数的差为零设 $a$ 和 $b$ 为两个相等的数，即 $a = b$。

我们要证明 $a - b = 0$。

题目三：证明两个相等数的乘积仍然相等设 $a$ 和 $b$ 为两个相等的数，即 $a = b$。

我们要证明 $a\cdot a = b \cdot b$。

题目四：证明两个相等数的商为1设 $a$ 和 $b$ 为两个相等的数，即 $a = b$。

我们要证明$\frac{a}{b} = 1$。

3. 解题思路对于以上的证明题目，我们可以使用代数运算规则来解决。

下面是每个题目的解题思路：题目一解题思路根据代数运算规则，我们知道相等的数可以互相代换。

所以，$a + a = a + b$。

又因为 $a = b$，所以 $a + b = b + b$。

因此，我们得出结论 $a + a = b + b$。

题目二解题思路根据代数运算规则，我们知道相等的数可以互相代换。

所以，$a - b = a - a$。

又因为 $a = b$，所以 $a - a = 0$。

因此，我们得出结论 $a - b = 0$。

题目三解题思路根据代数运算规则，我们知道相等的数可以互相代换。

所以，$a \cdot a = a \cdot b$。

又因为 $a = b$，所以 $a \cdot b = b \cdot b$。

因此，我们得出结论 $a \cdot a = b \cdot b$。

题目四解题思路根据代数运算规则，我们知道相等的数可以互相代换。

所以，$\frac{a}{b} = \frac{a}{a}$。

又因为 $a = b$，所以 $\frac{a}{a} = 1$。

七年级数学证明题目5则范文第一篇：七年级数学证明题目七年级数学证明题目1、如图，EF//AD，∠1＝∠2.说明：∠DGA+∠BAC=180°.请将说明过程填写完成.解：∵EF//AD，（已知）∴∠2＝_____.(_____________________________).又∵∠1＝∠2，（______）∴∠1＝∠3，（________________________）.∴AB//______，(____________________________)∴∠DGA+∠BAC=180°.(_____________________________)2、如图，AD为△ABC的中线，BE为△ABD的中线。

（8）（1）∠ABE=15°，∠BAD=40°，求∠BED的度数；A3、在△ABC中，已知∠ABC=66°，∠ACB=54°，BE是AC上的高，CF是AB上的高，H是BE和CF的交点，求∠ABE、∠ACF和∠BHC的度数.14、在△ABC中，∠A=（∠B＋∠C）、∠B－∠C=20°，求∠A、∠B、∠C的度数。

25、如图，已知∠DAB+∠D=180°，AC平分∠DAB，且∠CAD=25°，∠CB=95°（1）求∠DCA的度数；（2）求∠DCE的度数。

6、如图所示，请填写下列证明中的推理依据证明：∵∠A=∠C （已知），∴AB∥CD（___________________）∴∠ABO=∠CDO （_________________________）又∵DF平分∠CDO，BE平分∠ABO（已知）1∴∠1=∠CDO，∠2=∠ABO（_________________________）2∴∠1=∠2，∴DF∥BE （_____________________________________________）7、如图∆ABC中，AD是BC上的中线，BE是∆ABD中AD边上的中线，若∆ABC的面积是24，则∆ABE的面积是__？B8、完成下列推理，并填写理由如图4，∵ ∠ACE＝∠D（已知），∴∥（）．∴ ∠ACE＝∠FEC（已知），∴∥（）．∵ ∠AEC＝∠BOC（已知），∴∥（）．∵ ∠BFD＋∠FOC＝180°（已知），∴∥（）．AECD图49、已知，如图5，∠1+∠2=180°，∠3=108°，则∠4的度数是多少？10、如图6，AB∥CD，∠BAE=∠DCE=45°，求∠ED图411、如图，直线a∥b,点B在直线b上，且AB⊥BC,∠1=55°，则∠2的度数12、已知：AE平分△ABC的外角，且AE//BC，试判断∠B、∠C的大小关系，并说明理由13、已知：△ABC，射线BE、CF分别平分∠ABC和∠ACB，且BE、CF相交于点O。

初一数学证明题汇集(一)证明题练习1.如图，已知，，请问吗？请写出推理过程；2.如图，BD 是△ABC 的角平分线，DE ∥CB ，交AB 于点E ， ∠A =45°，∠BDC =60°，求△BDE 各内角的度数．3.如图，四边形ABCD 中， E 是AD 中点， C E 交BA 延长线于点F ，且CE ＝EF ．(1)试说明：CD ∥AB ；(2)若BE ⊥CF ，试说明：CF 平分∠BCD．AC AB ⊥,,12EF BC AD BC ⊥⊥∠=∠AC DG ⊥ADCB321EFG4. 如图,四边形ABCD 中,AC 交BD 于点O,则有这样的结论:AC+BD>AB+CD, 你能说出理由吗?5如图，AB=EB ，BC=BF ，.EF 和AC 相等吗?为什么?6.如图, AD ∥BC , AD 平分∠EAC,你能确定∠B 与∠C 的数量关系吗?请说明理由。

OADCB1D 2AECBCBF ABE ∠=∠7.如图,已知D 为△ABC 边BC 延长线上一点,DF ⊥AB 于F 交AC 于E,∠A=35°,∠D=42°,求∠ACD 的度数.8.如图，点E 、F 在正方形ABCD 的边BC 、CD 上，且BE=CF,试判断AE 、BF 的关系，并说明理由9.如图 AB=AC ，CD ⊥AB 于D ，BE ⊥AC 于E ，BE 与CD 相交于点O ．（1）求证AD=AE ；(2) 连接OA ，BC ，试判断直线OA ，BC 的关系并说明理由．FDCBEA(二)解方程组练习（1） （2）（3） （4）⎩⎨⎧=-=+524y x y x 22(1)2(2)24x y x y -=-⎧⎨-+-=⎩⎩⎨⎧-=-=+35y x y x ⎩⎨⎧=+=-732423y x y x（三）化简求解题练习1.先化简，再求值：，其中x =－1，y =0.52.先化简再求值：其中x=3先化简，再求值：；其中。