初一下数学证明经典例题及答案

七年级下册数学全等三角形证明题
1. 给定三角形ABC，其中∠BAC=90度，AD是BC上的中线。

证明：△ABD≌△ACD。

证明：
因为∠BAD=∠CAD，而又AD=AD（公共边），所以△ABD≌△ACD （SAS）。

2. 给定四边形ABCD，其中AB=BC，CD=DA，BD是AC的中线。

证明：△ABD≌△CBD，△BCD≌△DAB。

证明：
因为BD是AC的中线，所以BD=1/2AC。

又因为AB=BC，CD=DA，所以△ABD≌△CBD（SAS），△BCD≌△DAB（SAS）。

3. 给定三角形ABC和点D，使得∠BAD=∠ACD。

证明：
△ABD≌△ACD。

证明：
因为∠BAD=∠ACD，而又共有一边AD，所以△ABD≌△ACD（AAS）。

4. 给定三角形ABC和点D，使得AC=CD，∠ACB=∠ADB。

证明：△ACB≌△ADB。

证明：
由AC=CD可知∠ADC=∠ACD。

所以
∠ADB=∠ACB+∠ACD=∠ADB+∠ADC，即∠ADC=0。

因此，D与B重合，且AB=AB，AC=AD，所以△ACB≌△ADB（SSS）。

5. 给定三角形ABC和点D，使得AB=BD，CD是BC的中线。

证明：△ABD≌△ACD。

证明：
因为CD是BC的中线，所以CD=1/2BC。

又因为AB=BD，所以
∠ABD=∠ADB。

因此，△ABD≌△ACD（SAS）。

图①DA EC B Fl图②ABEF C lD 七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①，直线l 过正方形ABCD 的顶点B ，A 、C 两顶点在直线l 同侧，过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l ． (1)试说明：EF ＝AE ＋CF ；(2)如图②，当A 、C 两顶点在直线l 两侧时，其它条件不变，猜想EF 、AE 、CF 满足什么数量关系(直接写出答案，不必说明理由)．练习： 如图，△ABC 中，AB=AC ，∠BAC =90°．(1)过点A 任意一条直线l (l 不与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现它们之间有什么关系?试对这种关系说明理由； (2)过点A 任意作一条直线l (l 与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现经们之间有什么关系?试对这种关系说明理由．例2、已知正方形的四条边都相等，四个角都是90º。

如图，正方形ABCD 和正方形AEFG 有一个公共点A ，点G 、E 分别在线段AD 、AB 上。

（1）如图1， 连结DF 、BF ，说明：DF ＝BF ； （2）若将正方形AEFG 绕点A 按顺时针方向旋转，连结DG ，在旋转的过程中，你能否找到一条长度与线A E B图1D CG FA BD CGFE图2段DG 的长始终相等的线段？并以图2为例说明理由。

练习：如图，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，B 、C 、G 三点在一条直线上，且边长分别为2和3，在BG 上截取GP ＝2，连结AP 、PF. （1）观察猜想AP 与PF 之间的大小关系，并说明理由.（2）图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形？若存在，请说明变换过程；若不存在，请说明理由.（3）若把这个图形沿着PA 、PF 剪成三块，请你把它们拼成一个大正方形，在原图上（1）BD 与CE 相等吗？请说明理由．（2）你能求出BD与CE 的夹角∠BFC 的度数吗？（3）若将已知条件改为：四边形ABCD 与四边形AEFG 都是正方形，例3、正方形四边条边都相等，四个角都是90．如图，已知正方形ABCD 在直线MN 的上方，BC 在直线MN 上，点E 是直线MN 上一点，以AE 为边在直线MN 的上方作正方形AEFG ．（1）如图1，当点E 在线段BC 上（不与点B 、C 重合）时： ①判断△ADG 与△ABE 是否全等，并说明理由；②过点F 作FH ⊥MN ，垂足为点H ，观察并猜测线段BE 与线段CH 的数量关系，并说明理由；FB（2）如图2，当点E 在射线CN 上（不与点C 重合）时： ①判断△ADG 与△ABE 是否全等，不需说明理由；②过点F 作FH ⊥MN ，垂足为点H ，已知GD ＝4，求△CFH 的面积．练习：如图1，四边形ABCD 是正方形，G 是CD 边上的一个点(点G 与C 、D 不重合)，以CG 为一边作正方形CEFG ，连结BG ，DE ．（1）如图1，说明BG= DE 的理由（2）将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度 ，得到如图2．请你猜想①BG= DE 是否仍然成立？②BG 与DE 位置关系？并选取图2验证你的猜想．类型二、探究题例1、如图，已知等边△A B C 和点P ，设点P 到△A B C 三边A B 、A C 、B C （或其延长线）的距离分别为h 1、h 2、h 3，△A B C 的高为h ．图 2FG D A 图 1F G D A在图（1）中，点P 是边B C 的中点，此时h 3=0，可得结论：h h h h =++321． 在图（2）--（5）中，点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外．（1）请探究：图（2）--（5）中， h 1、h 2、h 3、h 之间的关系；（直接写出结论）（2）证明图（2）所得结论； （3）证明图（4）所得结论． （4）（附加题2分）在图（6）中，若四边形R B C S 是等腰梯形，∠B =∠C =60o ， R S =n ，B C =m ，点P 在梯形内，且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4，桥形的高为h ，则h 1、h 2、h 3、h 4、h 之间的关系为： ；图（4）与图（6）中的等式有何关系？练习：1、如图，在△ABC 中，AB=AC ，P 为底边上任意一点，PE ⊥AB ，PF ⊥AC ，BD ⊥AC.（1）求证：PE+PF=BD ；（2）若点P 是底边BC 的延长线上一点，其余条件不变，（1）中的结论还成立吗？如果成立，请说明理由；如果不成立，请画出图形，并探究它们的关系.2、如图，已知△ABC 三边长相等，和点P ，设点P 到△ABC 三边AB 、AC 、BC （或其A B C D EP A B C DE P M(3) A B C D EP M(2) A B C D EM (P )(1) A B C D E P M (5)C B APDEFC B E 延长线）的距离分别为h 1、h 2、h 3，△ABC 的高为h ．在图（1）中， 点P 是边BC 的中点，由S △ABP+S △ACP=S △ABC 得，h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0，所以：h h h h =++321．图（2）~（5）中，点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外．（1）请探究：图（2）~（5）中，h 1、h 2、h 3、h 之间的关系；⑵ ⑶ ⑷ ⑸ （2）说明图（2）所得结论为什么是正确的；例2、已知△ABC 是等边三角形，将一块含30角的直角三角板DEF 如图1放置，当点E 与点B 重合时，点A 恰好落在三角板的斜边DF 上. （1）AC=CF 吗? 为什么?（2）让三角板在BC 上向右平行移动，在三角板平行移动的过程中，(如图2)是否存在与线段EB 始终相等的线段（设AB ，AC 与三角板斜边的交点分别为G ，H ）？如果存在，请指出这条线段，并证明；如果不存在，请说明理由.(B)CE F图1ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)练习：1、如图1，一等腰直角三角尺GEF （∠EGF=90°,∠GEF=∠GFE=45°,GE=GF ）的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 相等吗？并说明理由；（2）若三角尺GEF 旋转到如图3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立吗？请说明理由．2、已知：△ABC 为等边三角形，M 是BC 延长线上一点，直角三角尺的一条直角边经过点A ，且60º角的顶点E 在BC 上滑动，（点E 不与点B 、C 重合），斜边∠ACM 的平分线CF 交于点F（1）如图（1）当点B 在BC 边得中点位置时（6分） ○1猜想AE 与BF 满足的数量关系是 。

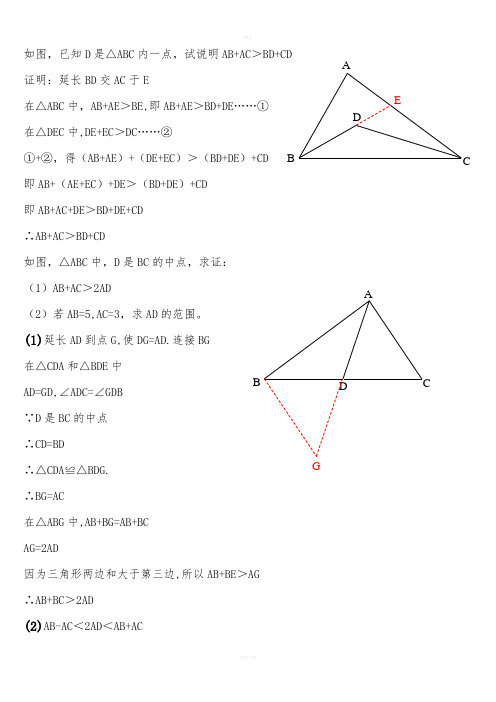
如图，已知D是△ABC内一点，试说明AB+AC＞BD+CD 证明：延长BD交AC于E在△ABC中，AB+AE＞BE,即AB+AE＞BD+DE……①在△DEC中,DE+EC＞DC……②①+②，得（AB+AE）+（DE+EC）＞（BD+DE）+CD 即AB+（AE+EC）+DE＞（BD+DE）+CD即AB+AC+DE＞BD+DE+CD∴AB+AC＞BD+CD如图，△ABC中，D是BC的中点，求证：（1）AB+AC＞2AD（2）若AB=5,AC=3，求AD的范围。

(1)延长AD到点G,使DG=AD.连接BG在△CDA和△BDE中AD=GD,∠ADC=∠GDB∵D是BC的中点∴CD=BD∴△CDA≌△BDG.∴BG=AC在△ABG中,AB+BG=AB+BCAG=2AD因为三角形两边和大于第三边,所以AB+BE＞AG ∴AB+BC＞2AD(2)AB-AC＜2AD＜AB+ACDC BAEAB CDG2＜2AD ＜8 1＜AD ＜4如图，AB=AD,AC=AE,∠BAD=∠CAE=90°，点F 为DE 的中点，求证：BC=2AF. 延长AF 到点G,使AF=DF.连接GD 在△AFE 和△DFG 中 AF=GF,∠AFE=∠DFG ∵点F 为DE 的中点 ∴DF=EF所以△AFE ≌△DFG. (SAS) GD=AE=AC;∠G=∠FAE.∴DG ∥AE.(内错角相等,两直线平行)则∠GDA+∠DAE=180°.(两直线平行,同旁内角互补） 又∵∠BAC+∠DAE=180°.∴∠GDA=∠BAC.(同角的补角相等). 又∵AD=AB.∴⊿ADG ≌⊿BAC(SAS) ∴AG=BC,即2AF=BC. ∴BC=2AF.如图，AD 是△ABC 的中线，点E 在BC 的延长线上，CE=AB, ∠BAC=∠BCA 求证：AE=2AD证明：在AD 的延长线上取点F,使AD ＝FD,连接CF ∵AD 是中线∴BD ＝CD,AD ＝FD,∠ADB ＝∠FDCECDBA∴△ABD≌△FCD （SAS）∴CF＝AB,∠B＝∠FCD∵∠ACF＝∠BCA+∠BCE,∠ACE＝∠BAC+∠B,∠BAC＝∠BCA∴∠ACF＝∠ACE∵CE＝AB∴CE＝CF∴△ACE≌△ACF （SAS）∴AE＝AF∵AF＝AD+FD＝2AD∴AE＝2AD如图，△ABC中，∠ABC=90°，AC=CE,BC=CD,∠ACE=∠BCD=90°，BC的延长线交DE于F。

初一典型几何证明题1、已知：AB=4，AC=2，D是BC中点，AD是整数，求AD解：延长A D到E,使AD=DE∵D是BC中点A ∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADC B CDBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=22、已知：BC=DE，∠B=∠E，∠C=∠D，F 是CD中点，求证：∠1=∠2A21B EC F D证明：连接BF和EF∵BC=ED,CF=DF∠,BCF=∠EDF∴△BCF≌△EDF (S.A.S)∴BF=EF,∠CBF=∠DEFB E连接在△BEF中,BF=EF∴∠EBF=∠BEF。

∵∠ABC=∠AED。

∴∠ABE=∠AEB。

∴AB=AE。

在△ABF和△AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴△ABF≌△AEF。

∴∠BAF=∠EAF (∠1=∠2)。

3、已知：∠1=∠2，CD=D，E EF//AB，求证：EF=ACA21FCDEB点G过C作CG∥EF交AD的延长线于CG∥EF，可得，∠EFD＝CGDDE＝DC∠FDE＝∠GDC（对顶角）∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC4、已知：AD平分∠BAC，AC=AB+B，D求证：∠B=2∠CA证明：延D E长AB取点E，使AE＝AC，连接∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5、已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：C F在AE上取F，使EF＝EB，连接∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，共22 页第3页∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6、如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

最新北师大版七年级下册三角形全等的证明练习题以及答案最新七年级下册三角形全等的证明1、已知：如图，四边形ABCD中，AC平分角BAD，CE垂直AB 于E，且角B+角D=180度，求证：AE=AD+BEA B DCE 122、已知，如图，AB=CD，DF⊥AC于F，BE⊥AC于E，DF=BE。

求证：AF=CE。

F EA CDB3、已知，如图，AB ⊥AC ，AB ＝AC ，AD ⊥AE ，AD ＝AE 。

求证：BE ＝CD 。

AEDCB4、如图，DE⊥AB，DF⊥AC，垂足分别为E、F，请你从下面三个条件中任选出两个作为已知条件，另一个为结论，推出一个正确的命题。

① AB=AC ② BD=CD ③ BE=CF5、如图，△ABC中，AB=AC，过A作GE∥BC，角平分线BD、CF交于点H，它们的延长线分别交GE于E、G，试在图中找出三对全等三角形，并对其中一对给出证明。

E6、如图，在△ＡＢＣ中，点Ｄ在ＡＢ上，点Ｅ在ＢＣ上，ＢＤ＝ＢＥ。

（１）请你再添加一个条件，使得△ＢＥＡ≌△ＢＤＣ，并给出证明。

你添加的条件是：________ ___（2）根据你添加的条件，再写出图中的一对全等三角形：______________（不再添加其他线段，不再标注或使用其他字母，不必写出证明过程）7、已知：如图，AB⊥BC，AD⊥DC，AB=AD，若E是AC上一点。

求证：EB=ED。

DA E CB8、已知：如图，AB、CD交于O点，CE//DF，CE=DF，AE=BF。

求证：∠ACE=∠BDF。

AB CDEFO9、已知：如图，△ABC中，AD⊥BC于D，E是AD上一点，BE的延长线交AC于F，若BD=AD，DE=DC。

求证：BF⊥AC。

AE FDB C10、. 已知：如图，△ABC 和△A ＇B ＇C ＇中，∠BAC=∠B ＇A ＇C ＇，∠B=∠B ＇，AD 、A ＇D ＇分别是∠BAC 、∠B ＇A ＇C ＇的平分线，且AD=A ＇D ＇。

初一下数学证明题(精选多篇)第一篇：初一下数学证明题初一下数学证明题6、如图，ce平分∠acb且ce⊥bd，∠dab=∠dba，ac=18，△cdb的周长是28。

求bd的长大家看我的步骤，我的步骤只做到这里就坐不下去了解：因为∠dab=∠dba(已知)所以ad=bd(等角对等边)因为ce平分∠acb，ce⊥bd(已知)所以∠dce=∠bce(角平分线的意义)∠bec=∠dec=90度(垂直意义)在△ace与△bce中因为{∠dce=∠bce(已求){ce=ec(公共边){∠bec=∠dec(已求)所以△ace≌△bce(a.s.a)所以bc=cd(全等三角形对应边相等)因为ac=18,即cd+ad=18所以cd+bd=18因为△cdb的周长是28，即cd+bd+bc=28所以bc=28-18=10所以cd=10所以bd=18-10=82在△abc中，已知∠cab=60°，d，e分别是边ab，ac上的点，且∠aed=60°，ed+db=ce，∠cdb=2∠cde，则∠dcb=()a.15°b.20°c.25°d.30°这题实际上是一传统题的翻版，原题中条件为△ade为等边三角形，c，b分别是ae，ad延长线的点，且ec=ab，求证;cd=cb，结论明确，本题增加了一个条件∠cdb=2∠cde，把结论改为求值题，其它改动没有多大变化，很快就会知道△ade为等边三角形，ec=ab，∠edc=∠cdb/2=40°，但结论为求值题后使结论没有目标，实际上是故弄玄虚，习难学生，使分析没有方向，要是学生没做过原题要得出正确结论是不大可能的!但学生可做一下投机;地图作得尽量正确，用量角器测一下也可得正确的结论。

但我觉得不会是供题者的本意吧。

故我认为对本题的改动看起来是改革，实为一败笔!不可取!但本题的原题我认为是一个能提高学生学习数学的兴趣与陪养学生创造性思维的好题题，现就原题给出若干分析请于指正。

如图，已知D 是△ABC 内一点，试说明AB+AC BD+CD证明：延长BD 交AC 于E在△ABC 中，AB+AE ＞BE,即AB+AE ＞BD+DE ……①在△DEC 中,DE+EC ＞DC ……②①+②，得（AB+AE ）+（DE+EC ）＞（BD+DE ）+CD即AB+（AE+EC ）+DE ＞（BD+DE ）+CD 即AB+AC+DE ＞BD+DE+CD ∴AB+AC ＞BD+CD如图，△ABC 中，D 是BC 的中点，求证： （1）AB+AC ＞2AD（2）若AB=5,AC=3，求AD 的范围。

(1)延长AD 到点G,使DG=AD.连接BG 在△CDA 和△BDE 中 AD=GD,∠ADC=∠GDB ∵D 是BC 的中点ABD∴CD=BD∴△CDA≌△BDG.∴BG=AC在△ABG中,AB+BG=AB+BCAG=2AD因为三角形两边和大于第三边,所以AB+BE＞AG∴AB+BC＞2AD(2)AB-AC＜2AD＜AB+AC2＜2AD＜81＜AD＜4如图，AB=AD,AC=AE,∠BAD=∠CAE=90°，点F为DE的中点，求证：BC=2AF.延长AF到点G,使AF=DF.连接GD 在△AFE和△DFG中AF=GF,∠AFE=∠DFG∵点F为DE的中点∴DF=EF所以△AFE≌△DFG.(SAS)GD=AE=AC;∠G=∠FAE.∴DG∥AE.(内错角相等,两直线平行)C则∠GDA+∠DAE=180°.(两直线平行,同旁内角互补）又∵∠BAC+∠DAE=180°.∴∠GDA=∠BAC.(同角的补角相等).又∵AD=AB.∴⊿ADG≌⊿BAC(SAS)∴AG=BC,即2AF=BC.∴BC=2AF.如图，AD是△ABC的中线，点E在BC的延长线上，CE=AB,∠BAC=∠BCA求证：AE=2AD证明：在AD的延长线上取点F,使AD＝FD,连接CF∵AD是中线∴BD＝CD,AD＝FD,∠ADB＝∠FDC∴△ABD≌△FCD （SAS）∴CF＝AB,∠B＝∠FCD∵∠ACF＝∠BCA+∠BCE,∠ACE＝∠BAC+∠B,∠BAC＝∠BCA∴∠ACF＝∠ACE FC DBA∵CE＝AB∴CE＝CF∴△ACE≌△ACF （SAS）∴AE＝AF∵AF＝AD+FD＝2AD∴AE＝2AD如图，△ABC中，∠ABC=90°，AC=CE,BC=CD,∠ACE=∠BCD=90°，BC的延长线交DE于F。